基于CDP模型的裝配式雙柱橋墩在低周往復加載下的力學性能研究
孫 秋 楊澤剛 張世誠 雷 笑
(1.南京市公路事業發展中心公路科學研究所 南京 210039; 2.河海大學土木與交通學院 南京 210098)
隨著我國生態保護及施工條件要求加強,低環境影響的橋梁施工方式逐漸得到青睞,節段預制裝配式橋梁便成為較佳的選擇。特別是橋梁經過環境敏感地區、橋位不易到達、氣候惡劣可供施工期較短等特殊狀況,或者要求通過快速施工來減少對周圍交通干擾、縮短阻塞時間、降低運輸車輛和施工中產生的各種噪聲時,預制節段裝配式橋梁可發揮較為理想的價值。
虎良[1]研究了節段鋼管混凝土纖維模型,對SA-CAP的受力特征提出計算模型概念,推導節段橋墩雙線性等效方法,分析了SA-CAP剛度退化數值計算及參數的影響;劉少乾[2]等研究鋼纖維自密實材料制作的混凝土橋墩對抗震性能的影響,通過建立模型數值模擬為計算提供理論依據;黃宜[3]對裝配式單柱墩進行擬靜力試驗,制作4組橋墩試件,研究不同連接形式的單柱式橋墩各項抗震性能指標。總體看來,我國目前對裝配式橋墩的研究多集中于單柱式橋墩,而對裝配式雙柱橋墩的研究較少。
本研究依托江蘇省第一座全預制裝配式橋梁,全橋采用分節預制技術,通過濕接縫、干接縫連接形成整體。其中下部結構采用雙柱框架式橋墩,利用灌漿套筒實現節段拼裝。為了研究其整體受力性能,本文采用混凝土塑性損傷模型與Clough鋼筋本構模型建立裝配式鋼筋混凝土橋墩的非線性分析模型,分析節段預制橋墩連接構件的性能規律;通過低周往復位移加載的方式,對裝配式橋墩的滯回耗能能力進行研究,研究雙柱實心橋墩的結構受力行為。
1 裝配式橋墩混凝土剛度退化性能本構關系
1.1 混凝土本構模型
混凝土本構關系采用混凝土塑性損傷模型(concrete damage plasticity,CDP)。CDP模型是依據Lee等[4]提出的損傷塑性模型,分析混凝土結構在循環和動力荷載作用下的一種分析模型。包括混凝土受壓與受拉本構關系、混凝土受壓及受拉的損傷因子,以及剛度恢復系數等部分。其中混凝土本構關系采用我國規范JTG 3362-2018[5]提供的混凝土本構關系。
本文損傷因子采用Sidiroff能量等價原理[6],損傷因子即為控制混凝土剛度退化的參數,用于定義混凝土損傷塑性材料模型的損傷特性。剛度恢復系數表示混凝土從受拉狀態轉入受壓狀態或受壓轉入受拉狀態時混凝土材料的剛度恢復程度。由于本研究是對墩柱的低周反復加載的模擬,混凝土會經歷拉、壓的反復作用,故此參數在模擬中顯得尤為重要。當wc=0時表示材料不能恢復剛度;當wc=1時,則表示材料完全恢復抗壓剛度;當wc在0~1之間時,則表示剛度只能部分恢復,剛度恢復系數曲線見圖1[7-8]。
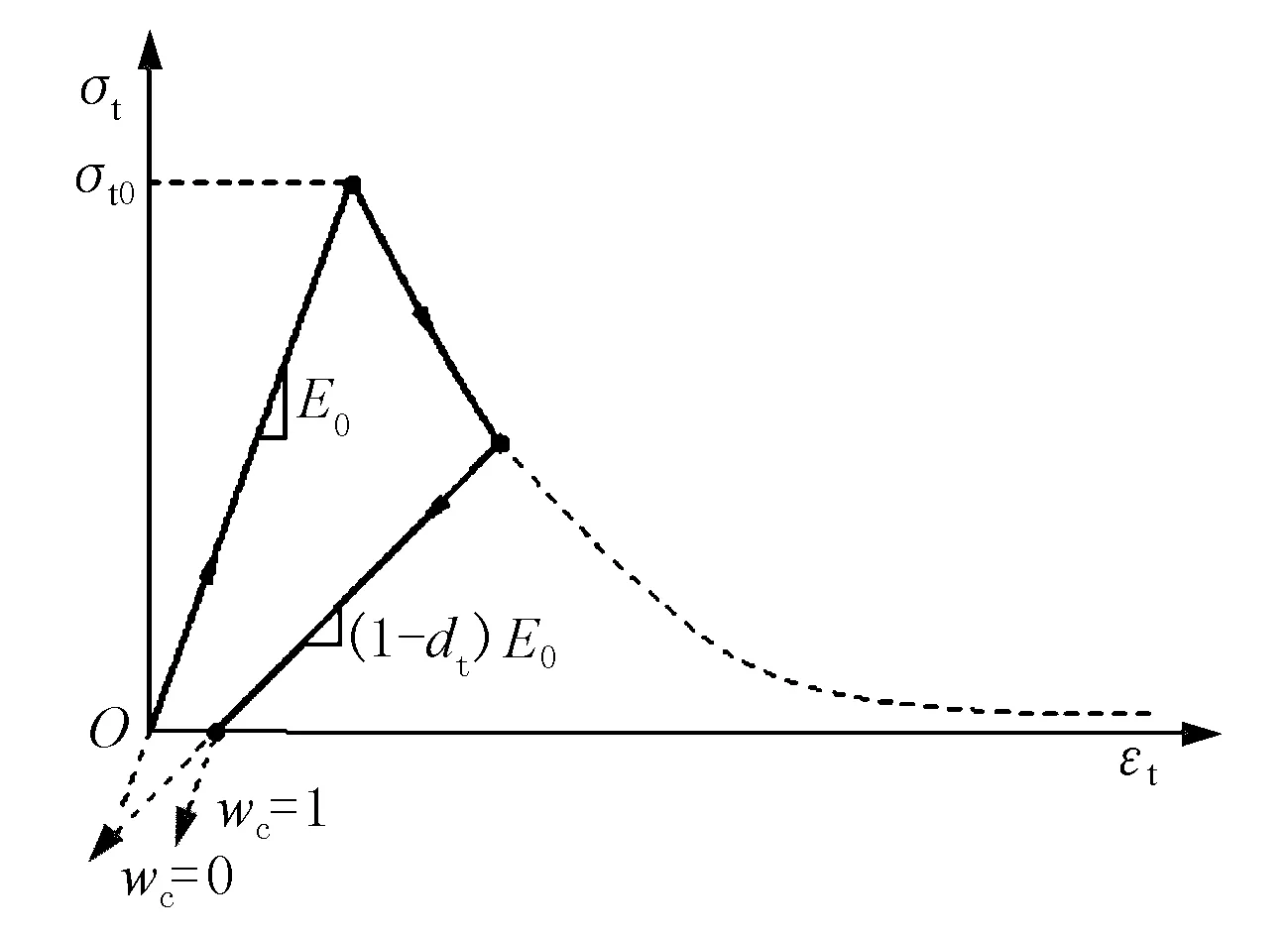
圖1 剛度恢復系數
受拉剛度恢復系數設置為0,即認為混凝土在受壓破壞后不能恢復受拉剛度。
為節省計算資源,同時不對結果產生較大影響,本文對混凝土受拉本構關系簡化設置:僅設置開裂應變及其對應的應力,不設置拉伸損傷因子,受壓剛度恢復系數設置為0.4,即拉裂后再次受壓時的受壓剛度將折減。若同壓縮損傷一樣設置較多損傷因子,則在拉伸損傷初步出現時程序即進入剛度矩陣的迭代,極其浪費計算資源,甚至導致計算的不收斂,且考慮拉伸損傷對計算結果的影響并不大。
1.2 鋼筋及套筒本構模型
鋼筋本構關系采用方自虎等[9]開發的子程序中的Clough鋼筋模型,即在加載剛度按Clough本構退化的隨動硬化單軸本構模型。該模型見圖2,其主要特點是在反向再加載時,并不立即指向歷史最大點,而是先按卸載剛度加載至歷史最大點對應應力的20%,再指向歷史最大點。該模型通過降低鋼筋強度來等效鋼筋與混凝土之間的黏結滑移作用,實現滯回曲線的“捏攏”效應。
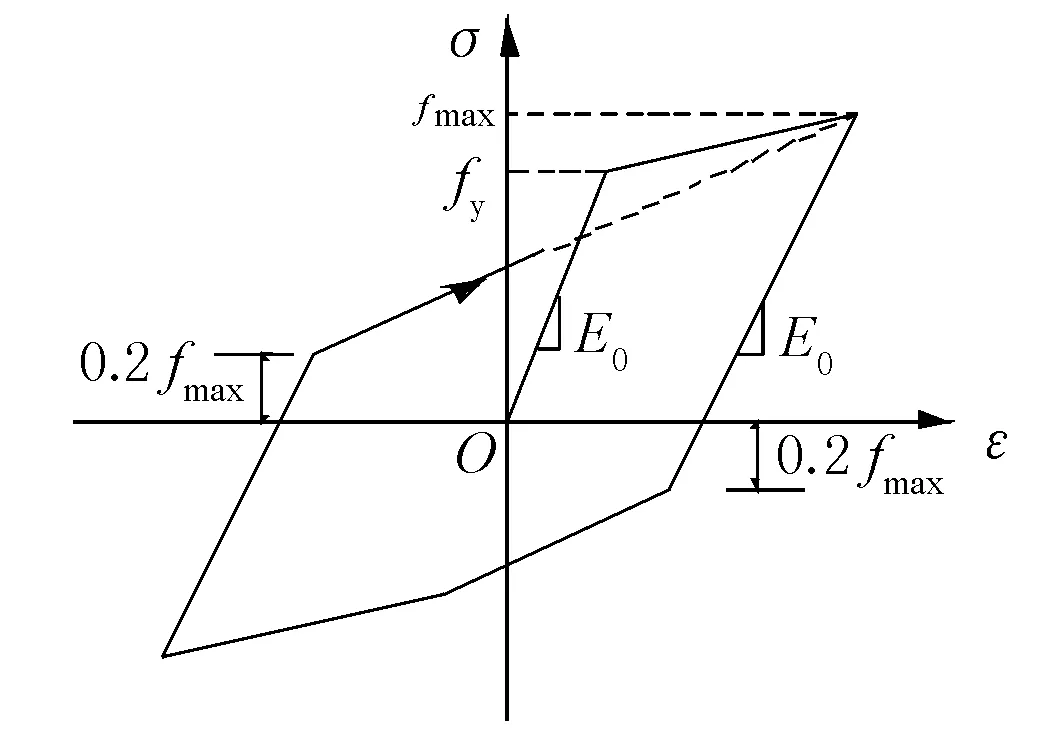
圖2 鋼筋隨動硬化單軸本構模型
灌漿套筒型號為上海寶生公司生產的GTZQ4 40型,材料為球墨鑄鐵,考慮其主要力學性能,采用雙折線模型,強度依據出廠時提供的相關數據設置,見圖3。
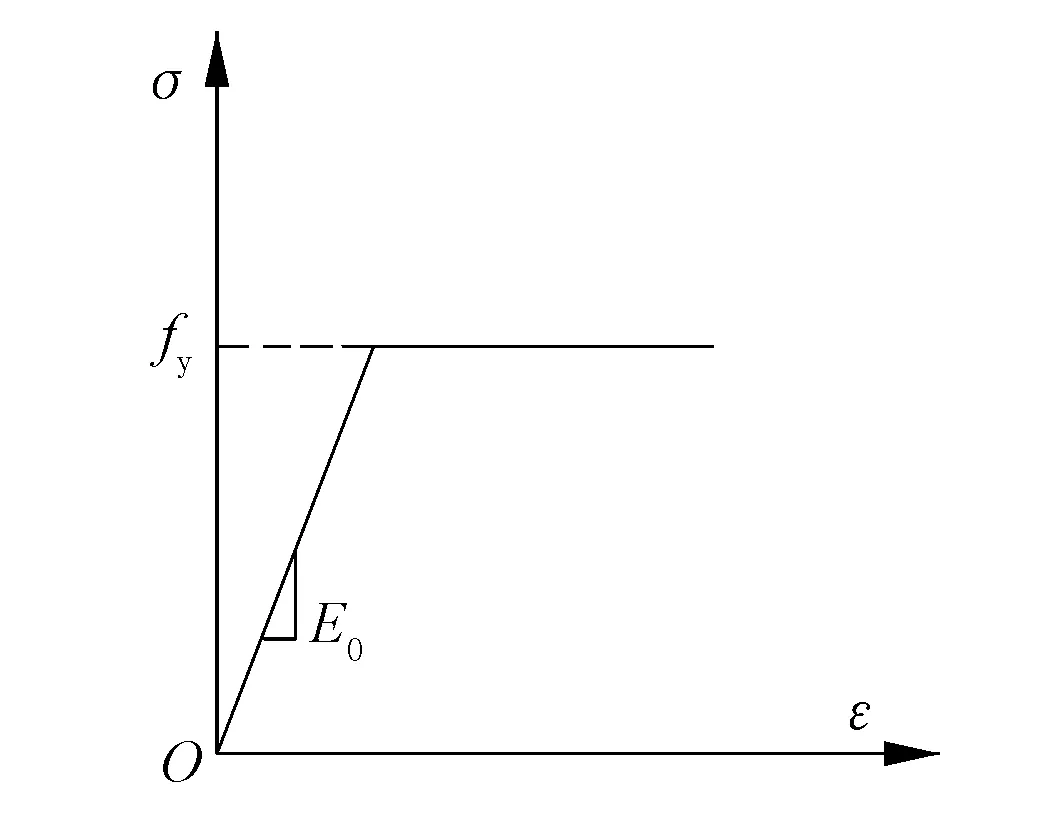
圖3 灌漿套筒本構關系
2 模型的建立與加載
該裝配式橋墩為雙柱型實心橋墩,柱高8 m,截面形式為2 m×2 m的正方形,長細比λ為6.8;配筋形式見圖4。鋼筋牌號均為HRB400,其中1號鋼筋直徑為20 mm,2a號鋼筋直徑為16 mm,3a號鋼筋直徑為12 mm,4a號鋼筋直徑為12 mm。墩柱與承臺通過灌漿套筒連接,與蓋梁通過金屬波紋管連接。

圖4 墩柱配筋圖(單位:cm)
本文關注點在橋墩與承臺的灌漿套筒連接位置,為節約計算資源,將其余部位進行簡化:認為蓋梁及承臺均為剛體,墩柱為變形體,材料選用CDP模型的C40混凝土;鋼筋采用HRB400的Clough鋼筋模型,縱筋配筋率為1.2%,建立模型見圖5。

圖5 ABAQUS有限元模型
模型中共建立3個分析步,初始分析步中將承臺底部約束激活,步驟1中施加豎直向下的力,大小為60 000 kN,軸壓比為0.39。步驟2中施加低周往復荷載,采用位移加載,加載幅值見圖6。
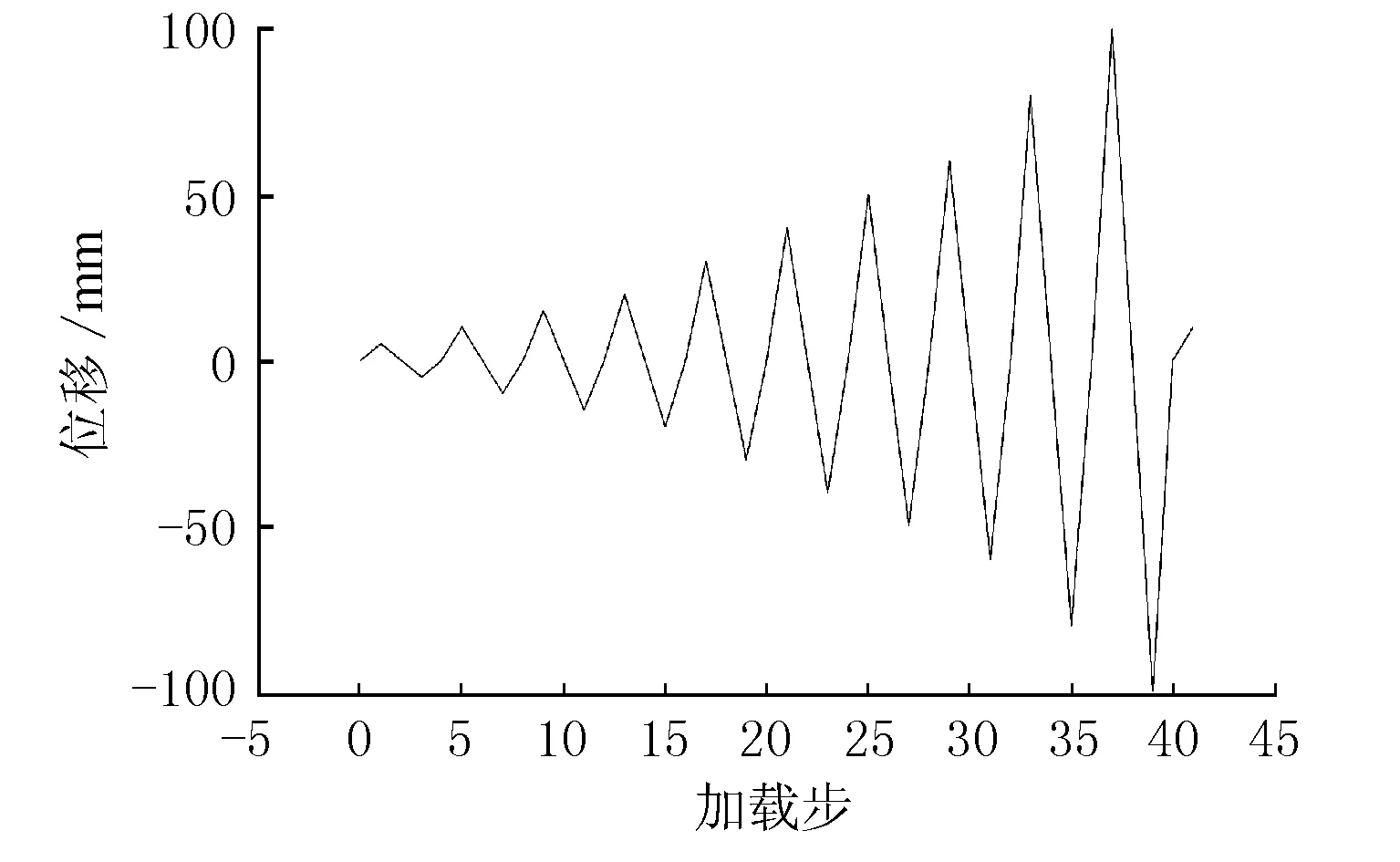
圖6 往復加載幅值
3 結果分析
3.1 混凝土受壓塑性損傷分析
對于鋼筋混凝土橋梁,延性是用來衡量橋梁抗震性能的一個重要指標,而鋼筋混凝土橋的延性是通過塑性鉸的形成和發展而獲得的,受外荷載作用時塑性鉸發生轉動,從而使橋墩獲得延性。對于雙柱墩而言,塑性鉸產生的區域出現在墩柱的頂部和底部[10]。
觀測橋墩從變形到破壞的全過程,其受壓損傷云圖見圖7。
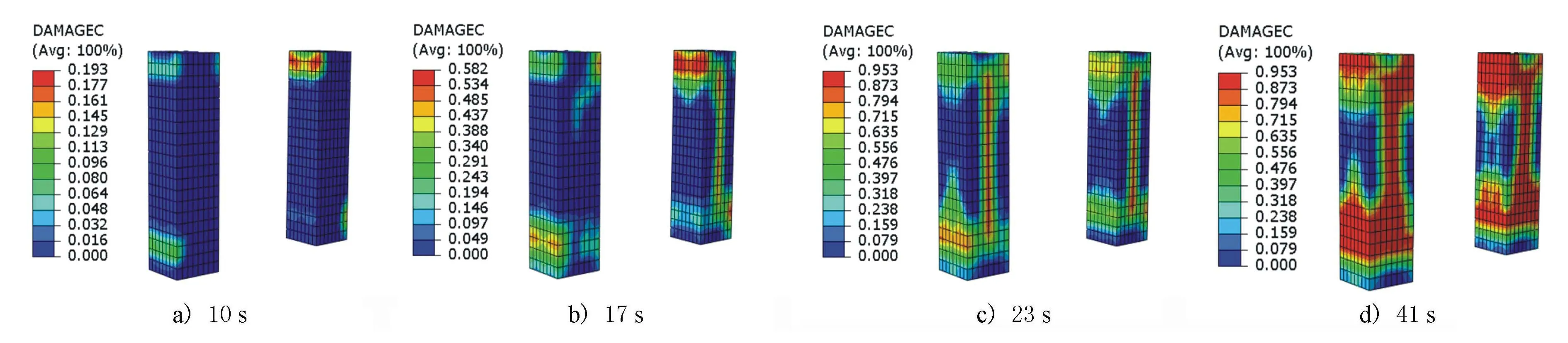
圖7 各階段受壓損傷云圖
由圖7可知:
1) 在加載至10 s時(加載最大位移值為15 mm)墩頂底開始出現不同程度的損傷,墩頂內側損傷為0.2,貼近蓋梁位置,墩底外側損傷值為0.1,位于墩底上方800 mm處,見圖7a)。這是由于墩底設置了高度為810 mm的灌漿套筒,加強了墩底的局部剛度,故混凝土受壓損傷從承臺上移至灌漿套筒上方位置。
2) 在加載至17 s時(加載最大位移值為30 mm)出現貫穿損傷,最大損傷位于墩底外側灌漿套筒的上方,受壓損傷大小為0.58,見圖7b)。
3) 在加載至23 s時(加載最大位移值為40 mm)最大損傷位于墩中部的貫穿損傷中,大小達到0.95,同時墩兩端的損傷也在不斷擴展,見圖7c),這意味著墩中部混凝土率先被完全壓壞。
4) 隨后的加載過程中墩上損傷不斷擴展,從墩兩端向墩中部延伸,中部貫穿裂縫向加載方向的兩側擴展,加載至41 s時(加載最大位移值為100 mm)損傷分布見圖7d)。
3.2 鋼筋應力分析
通過觀察橋墩從變形到破壞的全過程中縱筋與箍筋的應力云圖見圖9,可以得到以下結論。
1) 在加載至21 s時(加載最大位移值為40 mm)縱向鋼筋開始出現屈服現象,位于灌漿套筒內的墩柱鋼筋底部,見圖8a);此時位于墩兩端與墩中部的橫向箍筋呈現不同分布的屈服,見圖8b),與混凝土受壓損傷、此時的受力狀態一致。
2) 在加載至39 s時(加載最大位移值為100 mm)縱筋與箍筋大部分屈服,主要位于墩柱的兩端,見圖8c)、d),與最終混凝土損傷云圖類似。

圖8 各階段鋼筋von Mises應力
3.3 滯回曲線
本文對裝配式橋墩進行有限元分析,得到其滯回曲線見圖9。在構件混凝土未發生開裂塑性破壞之前,水平荷載與位移呈線性關系,曲線斜率隨著荷載值的增加未發生明顯的改變,即構件處于彈性階段。說明當構件處于彈性階段時,耗能小,橋墩模型卸載之后幾乎沒有殘余位移,剛度也沒有顯著的退化現象。結構構件產生破壞出現塑性變形時,滯回環的斜率隨著荷載值非線性的增加而逐漸減小,增加趨勢逐漸減緩,構件剛度出現退化現象,結構從屈服狀態逐漸發展至破壞狀態,剛度退化越來越明顯。
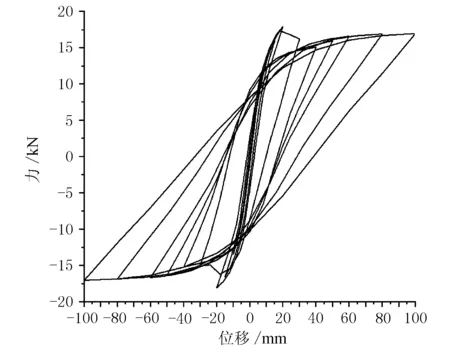
圖9 雙柱滯回曲線
4 結論
通過對實心雙柱裝配式混凝土橋墩實體進行有限元分析,得出如下結論。
1) 由于灌漿套筒的存在,加強了墩柱底部的局部強度,墩柱底部損傷上移至灌漿套筒上方;實心橋墩在低周往復加載下的主要損傷部位為橋墩上下兩端及沿加載方向的墩柱中部貫穿損傷,最終橋墩中部率先被壓壞失效,隨后損傷由橋墩兩端向中間擴展。
2) 墩柱往復加載時沿加載方向的箍筋中部率先屈服,最終縱筋的頂底部大范圍屈服,說明橋墩頂底部是往復加載的主要受力部位。
3) 實心墩柱的滯回曲線呈現出瘦長的“捏攏”現象并且在試件屈服后體現出剛度退化現象,滯回曲線的面積較小,耗能能力一般。這是由于墩柱為實心雙墩截面,且為短柱,剛度較大,對耗能不利。

