基于Drucker-Prager準則的水泥土統計損傷本構模型

李樹林 陳平奧 李 國

(1.貴州省交通規劃勘察設計研究院股份有限公司 貴陽 550081； 2.樂清市住房和城鄉建設局 樂清 325600)

水泥土廣泛應用于高速公路地基處理、防治凍脹融沉、基坑支護、堤壩截滲等方面，其應力-應變關系尤其是無側限抗壓強度對指導水泥土設計與施工具有重要意義。為探究水泥土本構模型，許多學者進行了卓有成效的研究。童小東等[1]通過進行試驗，研究了水泥土的損傷機制，得到了應力-應變、損傷變量等之間的關系曲線；薛慧君等[2]進行水泥土無側限抗壓強度試驗研究，通過擬合應力-應變關系曲線建立水泥土本構模型；陳四利等[3]對水泥土在飽水情形下進行宏觀、細觀破裂過程試驗研究，提出了相應的損傷本構模型。從研究可以看出，曹文貴等[4-5]在巖石本構模型中引入的統計損傷理論，不僅是巖石變形過程模擬最成功的方法之一，而且也在水泥土本構模型研究中取得了良好的成果。吳中俊[6]和陳鑫等[7]均基于不同的強度準則建立了水泥土統計損傷本構模型，準確度量水泥土微元強度是水泥土統計損傷本構模型建立的關鍵之一。

為此，本文將在上述研究的基礎上，基于統計損傷理論，引入在巖石統計損傷本構模型中應用廣泛且成效良好的Drucker-Prager準則來描述水泥土微元強度，探討水泥土應力-應變關系，使其更符合實際，以期完善水泥土本構關系的研究內容與方法。

1 水泥土統計損傷本構模型

現有研究已表明，基于統計損傷理論的水泥土本構模型方法可行，因此本文仍沿用該方法探討水泥土本構模型。依據Lemaitre應變等價性理論，可得

(1)

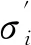
假定水泥土未損傷部分應力-應變關系服從虎克定律，且水泥土損傷部分與未損傷部分始終緊密結合，即

σi=(1-D)Eεi

(2)

式中：E為水泥土彈性模量；εi為應變。

式(2)即為水泥土本構模型，由此可以看出為利用該模型確定水泥土應力-應變關系，關鍵在于損傷變量D確定。

2 模型參數確定方法

受水泥土材料特性及其在固化過程中的各種影響因素如溫度等的影響，不可避免地其內部含有孔隙、裂縫等各種缺陷，這些缺陷具有極大的不均勻性，假設水泥土微元強度服從Weibull分布，這一假設在水泥土本構模型研究中已經證明切實可行，于是，損傷變量D可以表示為

D=1-exp[-(F/F0)m]

(3)

式中：m和F0為水泥土微元強度分布參數；F為水泥土微元強度。

因此，由式(3)可見，水泥土微元強度F的準確度量及水泥土微元強度分布參數m和F0的求解是確定損傷變量D的關鍵。

2.1 基于Drucker-Prager準則的水泥土微元強度

為使所建立本構模型更符合實際，與文獻[6]以軸向應變衡量水泥土微元強度不同，本文引入廣泛應用的Drucker-Prager準則[8]度量水泥土微元強度，其計算方法見式(4)～(7)。

(4)

(5)

(6)

(7)

式中：c為黏聚力；φ為內摩擦角。

對于水泥土無側限抗壓強度試驗，σ2=σ3=0，因此可得

I1=Eε1

(8)

(9)

將式(8)、(9)帶入式(4)，可得單軸壓縮條件下水泥土微元強度

(10)

2.2 損傷變量分布參數m和F0的確定方法

為確定參數m和F0，可依據水泥土應力-應變曲線峰值點特性，即該點應力-應變符合本構關系，且同時該點為曲線極值點，即

(11)

式中：σsc為峰值應力；εsc為峰值應變。

國家電網于2015年提出了全球能源互聯網發展構想,認為全球能源互聯網以智能電網、特高壓、清潔能源、全球視野為基本要素,將由跨國跨洲骨干網架和涵蓋各國各電壓等級電網的國家泛在智能電網組成,經過洲內互聯、跨洲互聯、全球互聯3個階段,各層級電網協調發展,堅持清潔發展和全球配置2個基本原則,具備網架堅強、廣泛互聯、高度智能、開放互動4個重要特征,實現能源傳輸、資源配置、市場交易、產業帶動和公共服務5個主要功能[2]。

將式(2)帶入式(11)可得

(12)

式中：Dsc為峰值點對應損傷變量。

由式(10)可得

(13)

由式(3)可得

(14)

由式(3)化簡可得

exp[-(F/F0)m]=1-D

(15)

(16)

將式(13)、(15)、(16)帶入式(14)，得

(17)

將式(17)帶入式(12)，可得m確定方法。

(18)

(19)

(20)

將式(18)帶入式(3)，可得F0確定方法。

(21)

3 實例分析

為驗證本文所建立的基于Drucker-Prager準則的水泥土統計損傷本構模型的合理性與可行性，引入文獻[2]中水泥土單軸壓縮試驗，對本文模型進行研究與分析。試驗資料給出了不同水泥摻量及齡期的水泥土彈性模量，本文模型參數確定步驟如下。

1) 通過擬合得出c、φ。

2) 由式(19)(20)計算得出Fsc和Dsc。

3) 將Fsc和Dsc帶入式(18)，計算得出本構模型參數m的值。

4) 將Fsc、Dsc和m帶入式(21)，計算得出本構模型參數F0的值。至此，本構模型已確定。各參數結果見表1。

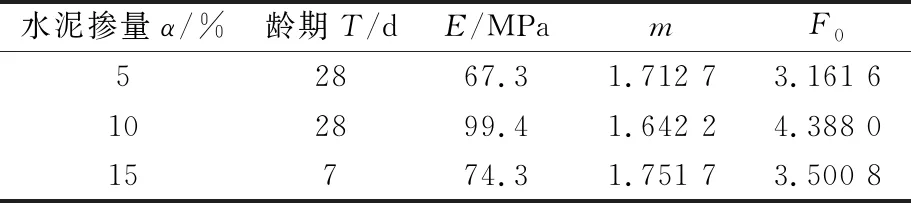
表1 水泥土本構模型參數

實測應力-應變值與理論應力-應變曲線見圖1。

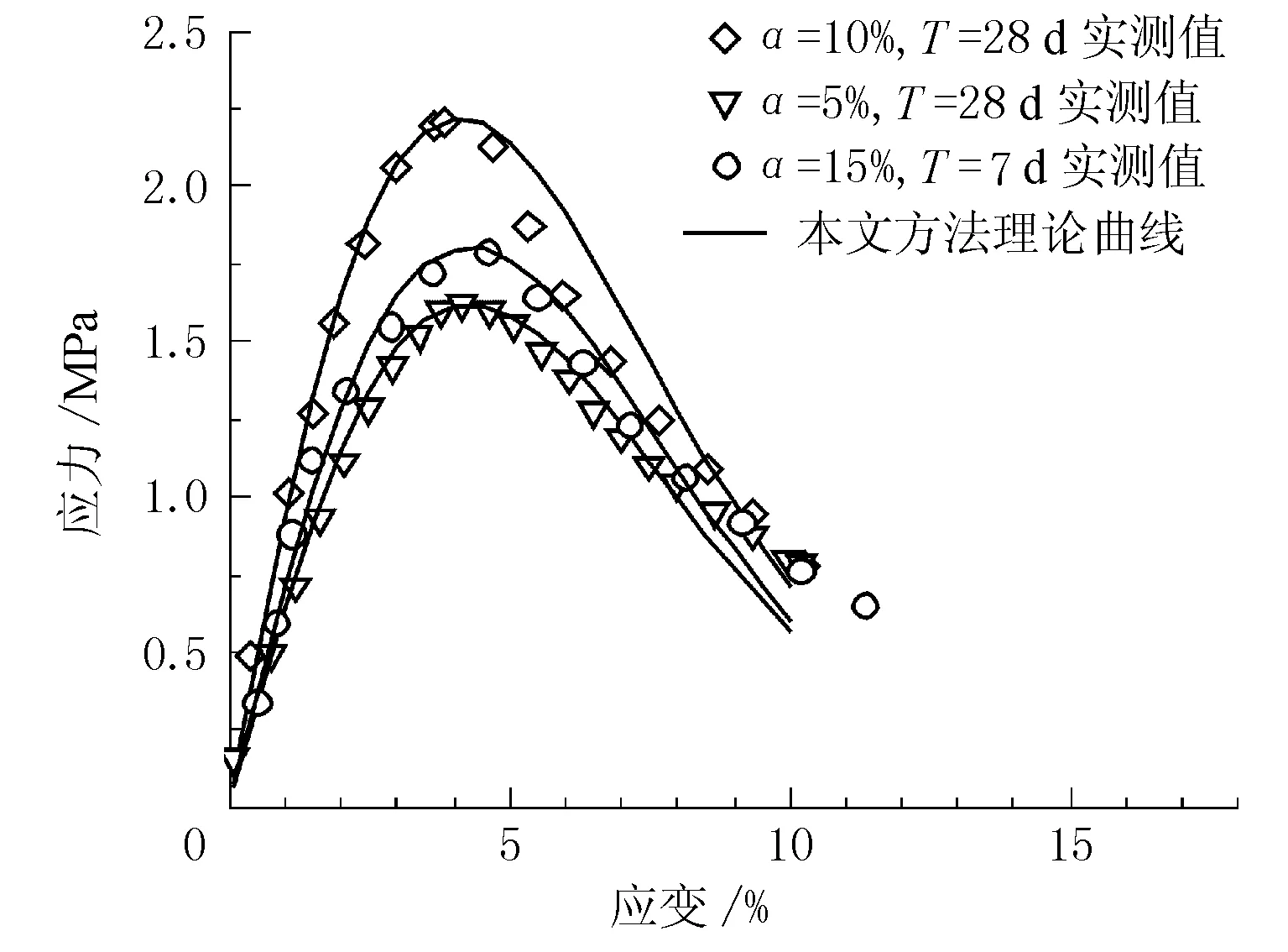
圖1 實測應力-應變值與理論應力-應變曲線

由圖1可見，各齡期與水泥摻量的水泥土應力-應變關系實測值與本文方法理論計算值在應力-應變曲線前段十分接近，而本文理論對水泥土應力-應變曲線的應變軟化現象的反映存在一定偏差，有待于進一步研究。圖2為損傷變量隨應變變化趨勢，隨著應變的不斷增加，水泥土內部損傷不斷加劇，直至完全損傷。

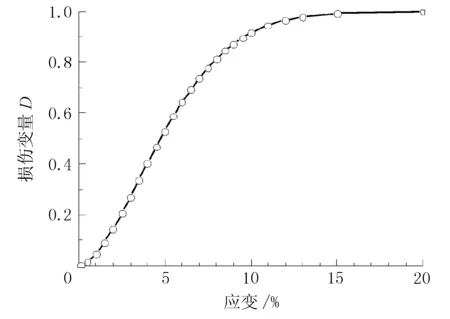
圖2 損傷變量與應變關系

4 結論

1) 引入統計損傷理論，假設水泥土微元強度服從雙參數Weibull分布，并且提出基于Drucker-Prager準則度量水泥土微元強度，建立了基于Drucker-Prager準則的水泥土統計損傷本構模型。

2) 由水泥土應力-應變曲線特點，峰值點應力-應變服從本構模型且該處導數為0，給出了模型參數確定方法。

3) 通過與水泥土單軸壓縮試驗對比，驗證了本文水泥土統計損傷模型的合理性與可行性。