兩款水泥混凝土路面結構有限元分析軟件接縫模擬技術比較*

武琨璐 蔣 鑫 古含焱 Babiker Lana Elabbas Abdelhaliem 付用國 邱延峻

(1.西南交通大學土木工程學院 成都 610031； 2.西南交通大學道路工程四川省重點實驗室 成都 610031；3. 西南交通大學高速鐵路線路工程教育部重點實驗室 成都 610031)

水泥混凝土路面結構所出現的唧泥、碎裂、錯臺和角隅斷裂等損害多與接縫密切相關[1]，接縫工作狀況嚴重制約著路面結構的使用性能。為了控制路面因溫縮應力和翹曲應力所引起的開裂，水泥混凝土路面面層在橫、縱2個方向設置接縫，通過集料嵌鎖或設置傳力桿和拉桿來傳遞部分荷載。路面接縫布置見圖1。

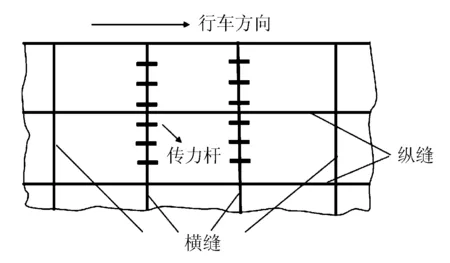
圖1 路面接縫布置示意

為深入研究接縫的傳荷效果，涌現出諸多有限元軟件可對接縫進行模擬，其中方法之一是直接視傳力桿、拉桿等為梁、桿等結構性單元，如ILLI-SLAB和JSLAB。將傳力桿看作二維梁單元，EverFE[1-2]中的傳力桿則由支承在混凝土彈性基礎上的剪切梁和彎曲梁共同模擬。對傳力桿予以細致建模雖可提高計算精度，但在有限元軟件中的實現和用戶操作方面等存在較大難度。若采用線性彈簧模型，認為接縫間傳遞的剪切力等于接縫兩側的撓度差與剪切彈簧常數的乘積，則更具實用性，可與接縫傳荷能力建立唯一對應關系。基于此法所開發的2D程序KENSLABS[3]、3D程序FEAFAA[4]各有特色，已得到廣泛應用，然而關于它們的接縫模擬技術的詳細討論尚鮮見報道。

本文擬針對內嵌于KENSLABS、FEAFAA這兩款程序的水泥混凝土路面結構接縫模擬技術開展橫向比較，通過具體算例，討論二者計算結果的差異及原因，有助于水泥混凝土路面結構分析工具的科學選用。

1 線性彈簧模型模擬接縫的基本原理

KENSLABS、FEAFAA均將接縫剛度與板和地基的剛度矩陣組合為路面結構的整體剛度矩陣，將外部作用的荷載轉換為節點力向量，即可通過求解方程(1)得到節點位移。

Kδ=F

(1)

式中：K為整體剛度矩陣；δ為節點位移；F為外部作用的節點力。

由上所述，在考慮利用有限元法模擬接縫時，核心工作在于求解接縫剛度。線性彈簧模型見圖2，相鄰板塊接縫兩側對應節點之間看作由線性彈簧相連。當受到外部荷載作用時，節點能夠承受豎向剪切力或彎矩作用。軟件通過確定接縫剛度的數值，使模型中節點彈簧常數與實際接縫剛度相同。

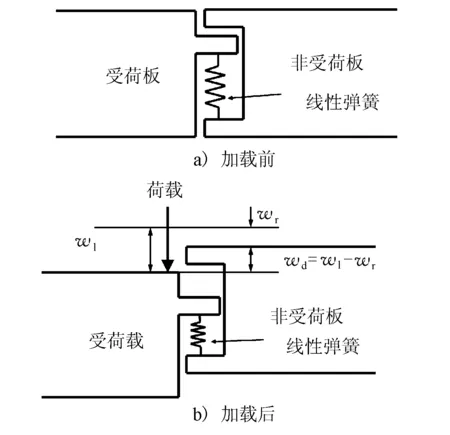
圖2 線性彈簧模型

其中KENSLABS在模擬集料嵌鎖型接縫時，接縫剛度由剪切彈簧常數和力矩彈簧常數表示；模擬傳力桿型接縫時由剪切彈簧常數表示[5]。而FEAFAA則默認為接縫僅傳遞豎向剪切力。剪切彈簧常數、彎矩彈簧常數的具體含義如下。

剪切彈簧常數Cw的計算式為

(2)

wd=wl-wr

(3)

式中：Fw為沿接縫處單位長度上的剪力；wd為接縫兩板之間的撓度差；wl為受荷板撓度值;wr為非受荷板撓度值。

彎矩彈簧常數Cθ的計算式為

(4)

式中：M為沿接縫處單位長度上的力矩；wθ為接縫兩板之間的轉角差。

計算接縫剛度的重點是確定沿接縫節點上彈簧常數的數值。接縫剛度受縫隙寬度、集料嚙合程度和斷面形狀等因素的影響，很多因素難以量化[6]。當縫隙寬度不大于3 mm時，多視為集料嵌鎖型接縫，此時彈簧常數由用戶自定義輸入，一般情況下在(0.5～4.0)×104MN/m3的范圍內取值。

而對于傳力桿型接縫剪切彈簧常數的確定，兩款軟件方法有所不同，下面分別詳細闡述。

1.1 KENSLABS接縫剛度計算

對于KENSLABS軟件，由于接縫中剪力作用導致兩板產生的撓度差wd由傳力桿自身的剪切變形ΔS和傳力桿作用下混凝土產生的變形y0共同組成，變形圖見圖3，可知它們之間的關系為

圖3 KENSLABS中傳力桿的剪切變形

wd=2y0+ΔS

(5)

接縫傳遞的剪切力Fw集中作用在沿接縫的節點上，L為沿接縫節點的平均間距，則可以得到

Fw=LCwwd

(6)

傳力桿的松動可通過傳力桿和混凝土之間的間隙wg予以考慮。若有間隙存在，則式(6)變為

Fw=LCw(wd-wg)

(7)

若傳力桿的平均間距為s, 則每個節點處傳力桿的數量為L/s，每根傳力桿上的剪力P為

(8)

傳力桿的剪切變形ΔS和傳力桿作用下混凝土的變形y0可以由式(9)和(12)計算得到。

(9)

(10)

(11)

(12)

式中：w為接縫寬度；G為傳力桿的剪切模量；γd為傳力桿的泊松比；A為傳力桿截面積；Ed、Id分別為傳力桿的彈性模量和截面慣性矩；β為混凝土與桿的相對剛度；K為混凝土對傳力桿的支承模量；d為傳力桿的直徑。

聯立以式(5)、(8)、(9)、(11)并與式(6)比較可得傳力桿接縫剪切彈簧常數Cw的計算公式為

(13)

1.2 FEAFAA接縫剛度計算

對于FEAFAA軟件，傳力桿接縫的傳荷作用由傳力桿截面的抗剪剛度和混凝土對傳力桿的承壓剛度組合而成。計算過程如下。

混凝土對傳力桿支承的剪切彈簧剛度DCI為

(14)

式中：β為混凝土與傳力桿的相對剛度，可由式(12)求出。

傳力桿自身的剪切彈簧剛度C為

(15)

(16)

式中：Az為傳力桿等效截面面積，取值為0.9A。

可得傳力桿組合剪切剛度為

(17)

式(17)分母第一項中的系數2表示同時考慮了受荷板和非受荷板對傳力桿的支承而產生的變形。

聯立式(14)～(17)得到單位長度上的剪切彈簧剛度的計算式為

(18)

2 兩款軟件模擬接縫實施技術

基于上述基本原理，下面詳細闡述這兩款軟件模擬接縫的具體實施技術。

2.1 面板分割

接縫傳荷效果在多塊板體系中方才涉及。KENSLABS最多可將面板結構劃分為9個板塊。通過“General”選項欄中的“NSLAB”設定板塊數量后，對板塊進行編號。每個板塊可有不同的尺寸，但相鄰的板寬度必須相同。劃分完成后對板塊單獨進行編號。

FEAFAA只能設置特定數量的板塊(1、2、4、6、9)，每個板塊具有相同的尺寸，無需進行編號。

2.2 接縫位置確定

KENSLABS通過“General”選項欄中的“NJOINT”中設定接縫數量，最多為12條。對每條接縫編號后，通過參數JONO(J,I)來確定接縫位置。其中第一個下標J(1,2,3,4)表示板的四邊(左、右、下和上)，第二個下標I表示板塊的編號。具體通過KENSLABS中“Slab”選項欄中點擊“Arrangement”，進行參數輸入。

FEAFAA通過勾選“Joint Modeling”欄中的“X-Direction Dowel Bar”或“Y-Direction Dowel Bar”選項，分別設置面板系統中的縱縫或橫縫。

2.3 接縫剛度確定

KENSLABS中每條接縫的剛度都可以在“Joint”項目欄中單獨設置。對于集料嵌鎖型接縫，輸入參數“SPCON1”和“SPCON2”，分別代表剪切彈簧常數Cw和彎矩彈簧常數Cθ，其余參數值為0。對于傳力桿型接縫，輸入參數“SCKV”“BD”“BS”“WJ”“GDC”“NNAJ”，分別表示混凝土對傳力桿的支承模量K、傳力桿的直徑d、平均間距s、接縫寬度w、傳力桿和混凝土之間的間隙wg、該接縫上的節點數N。若傳力桿等間距分布，“NNAJ”的值為0。否則輸入“NNAJ”確定接縫上節點數目后，雙擊數值框后輸入參數“BARNO”，代表沿該接縫每個節點上分布的傳力桿數目。傳力桿自身的材料性質，包括彈性模量Ed和泊松比γd分別在“Optional”選項欄“Dowel”中的“YMSB”和“PRSB”中設置，輸入界面見圖4。

圖4 KENSLABS中計算參數輸入界面

FEAFAA中每條接縫只能同時設置相同的接縫剛度。依次輸入傳力桿直徑d、間距s和接縫寬度w。輸入界面見圖5。

圖5 FEAFAA中計算參數輸入界面

混凝土對傳力桿的支承模量K有2個默認值，通過在“Method of Dowel Bar Placement(傳力桿的放置方式)”中進行選擇。勾選“Bar placed in fresh concrete(置于現澆混凝土中)”時，K=57 159.55 MPa(8 290 000 psi)；勾選“Bar placed in drilled holes(置于鉆孔中)”時，K=36 336.65 MPa(5 270 000 psi)。默認傳力桿的泊松比γd、彈性模量Ed分別為0.3、200 000 MPa(29 000 000 psi)。

2.4 模型計算求解

KENSLABS在運行過程中，根據總剛度矩陣維度是否小于70 000，分別采用高斯消去法、迭代法聯立求解方程式(1)。

FEAFAA首先調用INGRID程序劃分模型網格，生成輸入文件。之后調用計算引擎NIKE3D程序，使用迭代法和插值法計算出各個節點的位移和應力，以文本格式輸出。最后使用NIKEPLOT程序處理輸出數據，便于TecPlot軟件對其可視化。

2.5 接縫相關的計算結果后處理

KENSLABS中將計算結果輸出在.txt文件中。包括沿接縫上每個節點的剪力(FAJ1)和彎矩(FAJ2)、每根傳力桿上的剪力(FAJPD)、混凝土對傳力桿的支承應力(BEARS)和傳力桿的剪切應力(SHEARS)等，計算結果見圖6，可通過ORIGIN、SURFER等第三方軟件可視化。

圖6 KENSLABS接縫相關計算結果

FEAFAA將輸入數據和計算結果存放在n3dhsp文件中，計算結果見圖7。

圖7 FEAFAA接縫相關計算結果

然后調用NIKEPLOT程序，讀取n3dhsp文件并生成model_load.dat 和model_stress_1.dat。前者包含三維模型的幾何數據、荷載和邊界條件。后者包含單元節點坐標，以及外推到節點的6個應力分量、應力不變量和節點溫度。二者以特定的數據格式輸出，可通過TecPlot程序進行可視化。

3 算例分析與討論

3.1 問題描述

取設有橫縫的2塊板體系為研究對象。每塊板的長度、寬度和厚度分別為4，4，0.26 m。各結構層主要計算參數見表1。假設面層與水泥穩定基層之間光滑無摩阻，基層與地基之間為完全接觸。暫不考慮溫度翹曲和初始間隙的影響。

表1 各結構層主要計算參數

3.2 有限元模型建立

荷載系軸重100 kN的單軸雙輪組，輪胎接觸壓力為0.7 MPa[8]，作用范圍為18.9 cm×18.9 cm，兩側輪隙間距為190 cm。因板角破壞的情況最為常見，故將荷載作用在板角處[9]。接縫為寬度0.2 cm的脹縫，傳力桿直徑3.2 cm，等間距20 cm排布，傳力桿對混凝土的支承模量為57 172 MPa。假定傳力桿與混凝土之間無間隙。不考慮縱縫處拉桿的影響。

KENSLABS有限元模型見圖8。

圖8 KENSLABS路面結構有限元模型(單位：mm)

整個模型共劃分為88個單元、117個節點，滿足軟件的計算規模限制要求。單元最大長寬比為1 016/330=3.1<5，符合軟件精度要求。為了提高計算精度，荷載作用處網格劃分較密。

FEAFAA則采用非協調性八節點六面體磚單元進行建模，有限元模型見圖9。2個板塊、基層和地基的網格劃分均為35×35。地基使用無限單元進行模擬，劃分基層和地基網格時將每個單元邊長控制在12 in(304.8 mm)左右。

圖9 FEAFAA路面結構有限元模型(單位：mm)

3.3 計算結果分析

兩款軟件計算得到的板底應力分布結果比較見圖10。

圖10 面板底部主應力分布圖

由圖10可知，在荷載、路面結構參數相同的情況下，兩款軟件的計算結果宏觀規律保持一致。輪載下方板底受到壓應力，隨著與輪載中心距離的增大，面層底徑向應力由壓應力調整為拉應力。非受荷板中的最大拉應力大于受荷板中的最大拉應力。FEAFAA計算得到的板底最大壓應力較大，而最大拉應力較小。

路表彎沉的空間分布情況見圖11。圖11表明二者亦相似。采用以撓度比表征的傳荷系數LTE來評價接縫傳荷能力，計算結果見表2。KENSLABS和FEAFAA計算得到的傳荷系數分別為93.1%，97.2%。

圖11 路表彎沉的空間分布

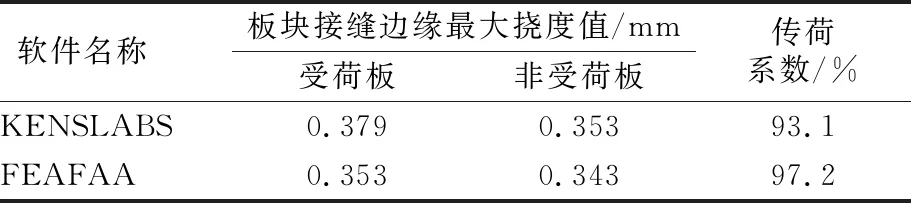
表2 板塊接縫邊緣最大撓度值及接縫傳荷系數

兩款軟件接縫模擬技術不同導致計算結果產生差異，體現在以下兩方面。

1) 對比式(13)、式(18)，KENSLABS未考慮傳力桿接縫間隙部分對抗彎剛度的貢獻，剪切彈簧剛度計算值小于FEAFAA。對于縫隙寬度較小的傳力桿接縫來說，該影響可忽略不計。

2) 網格劃分對計算結果的收斂性和精度影響甚大[10]。在板塊沿接縫兩側進行節點排布時，KENSLABS受半帶寬的限制，靠近荷載周圍節點緊密排布，遠離荷載區域則比較稀疏；FEAFAA則可以劃分大量等距離節點，適當提高了精確度。

4 結論

1) 模擬縫隙寬度較大的傳力桿型接縫，或為提高計算精度，網格劃分細密時，總剛度矩陣維度較大，使用FEAFAA將體現出一定的優越性。

2) 若不同位置接縫中傳力桿自身的彈性性能參數與常規數值不同或不等間距分布時，宜采用KENSLABS。

3) KENSLABS的結果數據量較少，易于用多種第三方軟件對結果進行可視化處理。FEAFAA的結果數據量較多，雖易被TecPlot讀取處理，但要求用戶熟悉TecPlot軟件，若要使用其他第三方軟件處理則要求用戶重新編排數據格式，稍為繁瑣。