針對WRF模式中行星邊界層參數化過程傾向項的擾動方法

武天杰 閔錦忠

摘要 針對WRF模式中行星邊界層參數化過程中的不確定性，發展了一種針對行星邊界層參數化過程的隨機物理擾動方案（SPPBLPT），該方案針對行星邊界層計算的溫度、風場、水汽傾向項進行擾動。使用該方案、多行星邊界層參數化方案、多參數擾動方案及針對WRF模式總傾向的隨機物理過程擾動（SPPT）方案對2014年7月進行對比實驗，發現使用較大格點方差的SPPBLPT方案能有效降低地面溫度與風場的誤差，也能降低降水的預報誤差，而其他方案對預報改善不明顯。針對地面溫度和風場的BS評分顯示，SPPBLPT方案通過降低可靠性評分（提高可靠性），顯著改善了集合預報對溫度與風場的可能性預報，同時該方案能顯著提高降水的GSS評分，在所有實驗中，較大格點方差的SPPBLPT方案表現最好。針對行星邊界層參數化過程的隨機物理擾動方案（SPPBLPT）能顯著提升集合預報系統性能，但是該方案的擾動參數的設置還需要進一步研究。

關鍵詞 行星邊界層;隨機物理過程擾動;集合預報;WRF模式

數值模式已被廣泛用于天氣系統的預報和科研當中，這些模式中，對于無法被完全解析的次網格過程，常常使用參數化過程來表征。行星邊界層方案（Planetary Boundary Layer，PBL）是這些參數化過程中的一種，用于表征行星邊界層及自由大氣中次網格的熱量、水汽、動量等物理量的垂直湍流輸送。Lamraoui et al.（2019）研究指出模式（Weather Research and Forecasting Model）中不同PBL參數化方案，會影響數值模式對鋒前云雨現象的模擬。代昕鷺等（2017）研究指出，PBL參數化方案在中尺度WARMS模式和WRF模式中，對降水都有較大的影響。Hariprasad et al.（2014）指出PBL通過對湍流混合的模擬影響模式的底層溫濕的模擬。Li and Pu（2008）指出WRF模式在模擬臺風Emily（2005）時，PBL參數化的選擇會顯著影響臺風的突然增強過程。

模式中PBL方案對中小尺度天氣系統有重要的影響，許多學者改進PBL方案、甚至提出新的PBL參數化方案，從而提高PBL參數化對天氣系統模擬的準確性（Chen and Dudhia，2001;Pleim，2007;Cohen et al.，2015）。但因為大氣的高度非線性及復雜性，繼續提高PBL方案的準確性存在一定的困難。提高模式分辨率也可以在一定程度上提高模式PBL參數化過程的性能，但一味提高分辨率不僅會遇到灰區（gray-zone）問題，同時也會大幅增加計算成本。在確定性預報中改進PBL參數化過程是極大的挑戰。

多項研究表明，集合預報是克服單一確定性預報的局限性的一種有效方法（吳增茂和張新玲，2000;杜鈞，2002;狄靖月等，2013;閔錦忠和房麗娟，2017;李曉莉等，2019;朱躍建，2020）。近年來，有限區域中尺度集合預報取得了巨大的進步（陳靜等，2005;Bowler and Mylne，2009;Wang et al.，2011;陳耀登等，2014;陳浩等，2017）。針對參數化過程對大氣描述的不準確給模式帶來的誤差，用的集合預報方案有多物理過程擾動法、多參數擾動法。在集合預報中使用多個PBL方案，或者針對某一特定的PBL方案，使用不同的參數值，可以提升集合預報系統的離散度。但是使用固定的PBL方案或參數組合是盲目的。現今比較流行的集合預報方案是隨機擾動參數化傾向方案（Stochastically Perturbed Parameterization Tendencies，SPPT）。該方法是針對模式中所有參數化的誤差總和進行估計和擾動的一種方法，理論依據是隨著模式分辨率的提高，參數化方案對次網格表達使用“平均”的方案不再適用，應使用“采樣”的方法。這種方法在氣候預測中可以一定程度上提高預報的效果。Berner et al.（2015）將該方法引入WRF模式，發現這種方法對中小尺度天氣系統也有一定的改良作用。Romine et al.（2014）、Berner et al.（2015）對在WRF模式中進行了一個月的模擬，發現該方法在一定程度上提高了集合離散度及技巧評分，同時對極端天氣的概率評分也有所提高。與傳統的多物理或多參數方法相比，SPPT克服了這些方法的主觀性，即對物理過程或參數選擇是人為主觀的，同時也克服了這些方法會導致每個成員平均氣候態不同的問題，優勢明顯。但該方法的缺點是并不考慮各種參數化之間的影響，忽略了不同參數化方案的相互作用（Christensen et al.，2015）。

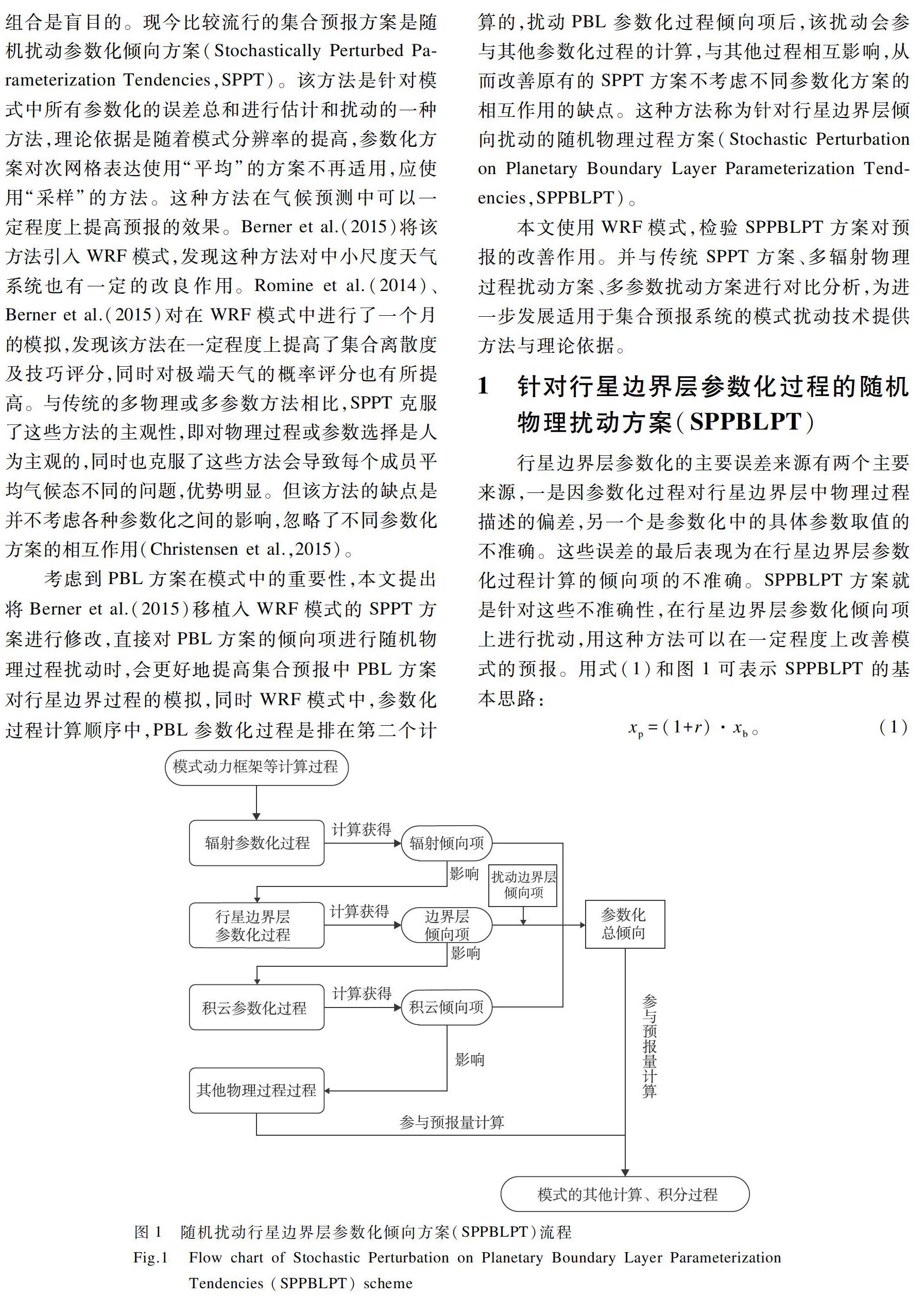
考慮到PBL方案在模式中的重要性，本文提出將Berner et al.（2015）移植入WRF模式的SPPT方案進行修改，直接對PBL方案的傾向項進行隨機物理過程擾動時，會更好地提高集合預報中PBL方案對行星邊界過程的模擬，同時WRF模式中，參數化過程計算順序中，PBL參數化過程是排在第二個計算的，擾動PBL參數化過程傾向項后，該擾動會參與其他參數化過程的計算，與其他過程相互影響，從而改善原有的SPPT方案不考慮不同參數化方案的相互作用的缺點。這種方法稱為針對行星邊界層傾向擾動的隨機物理過程方案（Stochastic Perturbation on Planetary Boundary Layer Parameterization Tendencies，SPPBLPT）。

本文使用WRF模式，檢驗SPPBLPT方案對預報的改善作用。并與傳統SPPT方案、多輻射物理過程擾動方案、多參數擾動方案進行對比分析，為進一步發展適用于集合預報系統的模式擾動技術提供方法與理論依據。

1 針對行星邊界層參數化過程的隨機物理擾動方案（SPPBLPT）

行星邊界層參數化的主要誤差來源有兩個主要來源，一是因參數化過程對行星邊界層中物理過程描述的偏差，另一個是參數化中的具體參數取值的不準確。這些誤差的最后表現為在行星邊界層參數化過程計算的傾向項的不準確。SPPBLPT方案就是針對這些不準確性，在行星邊界層參數化傾向項上進行擾動，用這種方法可以在一定程度上改善模式的預報。用式（1）和圖1可表示SPPBLPT的基本思路：

xp=（1+r）·xb。 ?（1）

式中：xb為WRF模式中行星邊界層參數化方案計算所得傾向項;r為擾動場;xp為擾動后的傾向項。

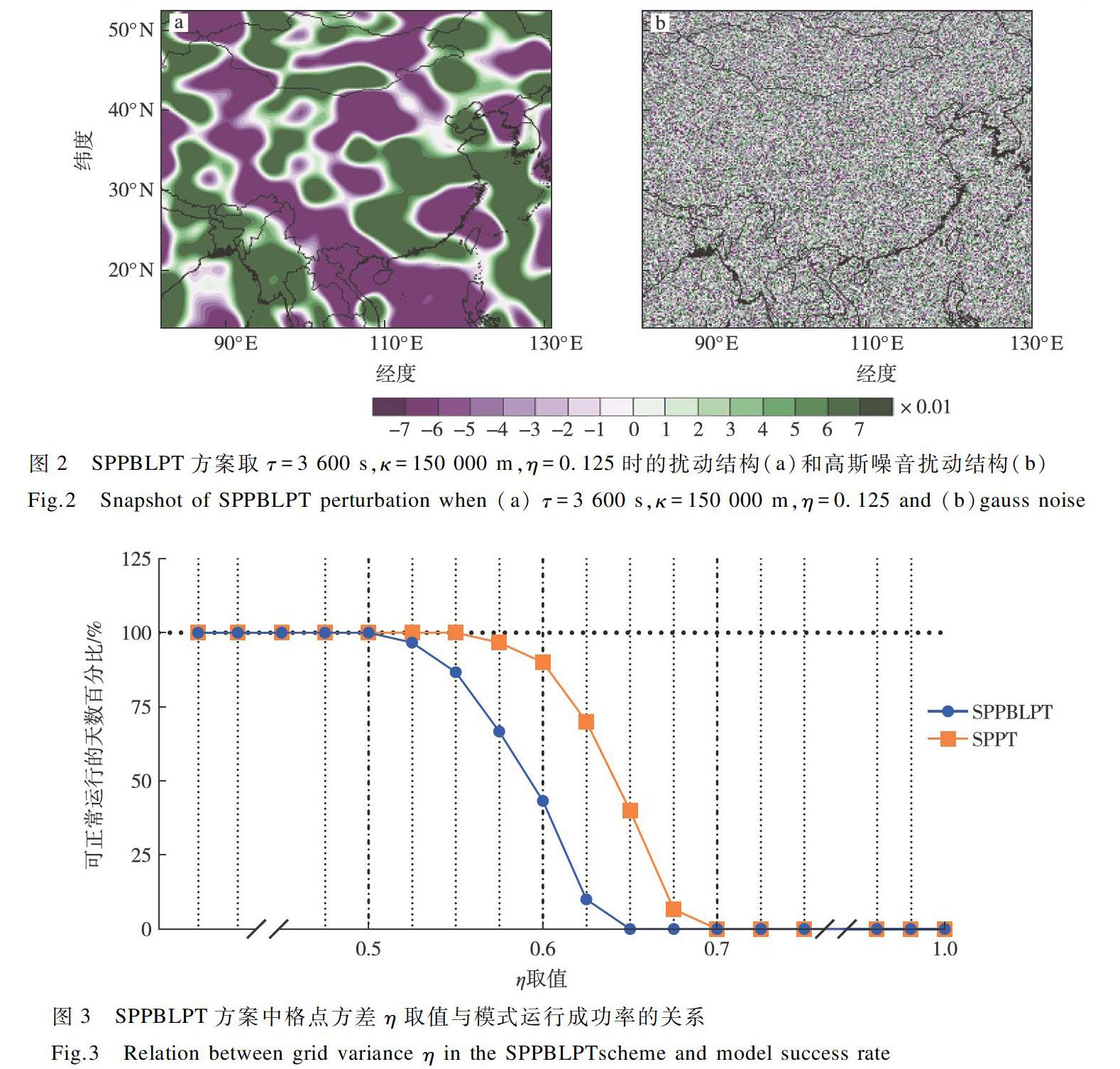
在WRF模式中，行星邊界層參數化方案會計算出溫度傾向、風場（U方向和V方向）傾向，水汽傾向，故SPPBLPT方案分別對這四種傾向進行擾動。為了防止非必要的重力波的產生，同時防止擾動后的變量不匹配，擾動四種不同傾向的擾動場r是相同的。同時從式（1）可以看出，如何合理的產生擾動場r是SPPBLPT方案的一個關鍵環節。參考Berner et al.（2015）提出的擾動方案生成擾動場r。這種擾動與高斯噪音不同，它具有一定的時空特征。圖2展示了這種擾動場的結構與高斯噪音的比對。生成擾動場的隨機數種子不同，便可生成每個成員不同的擾動場，以估計PBL方案可能的誤差。為了調整擾動場的時空特征，SPPBLPT方案有三個關鍵參數，分別是：去相關時間τ，去相關尺度κ和格點上的方差η（Berner et al.，2015）。其中參數τ與參數κ可以確定擾動場的時空特征，這種特征通常由模擬的天氣系統和季節所決定，故本文參考Romine et al.（2014），設置τ=3 600 s，κ=150 km。格點方差η的作用是確定擾動量的大小。根據Berner et al.（2015）研究結果，較大的η通常會導致模式有較大的離散度，但是會讓模式更容易崩潰。為了確定模式可接受的最大η值，故本文用不同的η值在研究時段使用SPPBLPT方案運行WRF模式，尋找最大可能的值，結果如圖3所示。故η取值為0.5。為了驗證這種取值是否合理，本文使用了Romine et al.（2014）文中取值η=0.125。

2 實驗設計

2.1 控制實驗

選取2014年7月1—30日作為研究對象，選取如圖4所示的范圍作為研究區域。在該研究區域和時段內，有多次暴雨過程、氣象干旱、臺風活動，也包含了晴天和不明顯的天氣過程。作為研究SPPBLPT方案對集合預報的改善作用比較合適。控制實驗的初始場使用NCEP1°×1°全球再分析資料，生成12組初始場形成12個集合預報成員。控制實驗從12時（世界時）啟動模式，向后積分36 h，相當于每個成員需要分30次積分過程。控制實驗中，模式使用的長、短波參數化方案為RRTMG方案，微物理參數化方案為WSM 6-class graupel方案，積云參數化方案為Kain-Fritsch方案，陸面參數化為Unified Noah land-surface方案，PBL方案采用YSU方案。

2.2 SPPBLPT實驗

針對PBL造成的不確定性，使用SPPBLPT方案進行集合預報。本文對WRF3.7.1模式進行修改，將SPPBLPT方案植入WRF模式中，由“namelist.input”輸入文件控制該方案的開關和設置項。SPPBLPT實驗的所有設置與控制實驗一致，但開啟了PBL傾向擾動功能。生成擾動噪音的參數均參考Romine et al.（2014）中的設置τ=3 600 s，η=150 km。為了驗證擾動方案中η取值的影響，按照Romine et al.（2014）文中設置的0.125與前文中測試得出的0.5分別進行實驗。其中η取0.125的實驗被稱為SPPBLPT實驗，η取0.5的實驗被稱為SPPBLPT5實驗。

2.3 對照實驗

為了研究SPPBLPT方案在集合預報中對模式性能的改善，以及其比一些常用集合預報方案的改進，引入了一批對比實驗與之對比。同時為了驗證對PBL參數化方案傾向項直接擾動比擾動模式的總傾向更有效，也引入原始的SPPT方案作為對照試驗。

2.3.1 多PBL參數化過程擾動實驗與多參數擾動實驗

作為較為成熟的WRF模式，包含了多種PBL方案用于預報或研究。這些方案對PBL過程有不同的描述。在集合預報系統中使用不同PBL參數化過程，是較為常用的估計PBL參數化方案的誤差并提高集合預報系統性能的一種方法。為了構建多PBL參數化過程擾動實驗，本文采用6中不同的PBL方案，該實驗在本文中被稱為MULTI實驗。該方案使用的PBL參數化過程列在表（1）中。

2.3.2 多參數擾動實驗

控制實驗中的YSU方案包含很多可調參數，這些參數的默認取值多是通過案例研究或理論推導的經驗值獲得。用經驗取得的參數是導致模式預報誤差的重要因素之一。各種參數的敏感性對集合預報系統影響不同。本文根據Di et al.（2015）的研究，選取一個YSU方案中較為敏感的參數，即用于計算動量擴散系數的廓線形狀指數pfac（profile shape exponent for calculating themomentum diffusivity coefficient），也選取了一個YSU方案中不太敏感的參數，即路面邊界層的臨界理查森數brcr_sb（Critical Richardson number for boundary layer of land）。pfac合理取值范圍為[1，3]，brcr_sb合理取值范圍為[0.125，0.5]，對照實驗在相應的取值范圍內，設置合適的參數值，形成不同成員，這些參數的取值和組合列在表（1）中。擾動pfac的實驗命名為PBL_pfac，擾動brcr_sb的實驗命名為PBL_brcrsb。

2.3.3 WRF自帶的SPPT擾動實驗

本文中SPPBLPT方案是基于WRF3.7.1版本中SPPT方案修改而來，認為單獨擾動邊界層參數化方案比擾動參數化總傾向要好，故使用原始的SPPT方案與新的SPPBLPT方案進行對比。SPPT方案的擾動參數設置與SPPBLPT方案一致，其中η取0.125的實驗被稱為MSPPT實驗，η取0.5的實驗被稱為MSPPT5實驗。

本文中所有的實驗列在表2中。

FSS評分中，N是鄰域的大小，根據潘留杰等（2015）的研究結果，該值的取值影響評分數值，但不影響評分的趨勢與對比。〈Pf〉s是預報中超過閾值鄰域的格點的比例，〈Po〉s是觀測中超過閾值鄰域的格點的比例。如果FSS評分為1，表明預報和觀測的事件完全重合，效果最好。

使用顯著性檢驗確定SPPBLPT對集合預報系統的預報結果是否有顯著的意義，但因為樣本數量較少，本文使用自助法（bootstrap;Hamill，1999）進行50次隨機抽樣。若對比的集合預報方案經過自助法隨機抽樣后，與控制實驗的差異通過置信度為95%的顯著檢驗，則認為結果與控制實驗相比具有顯著的區別。

4 結果檢驗與分析

4.1 地面溫度風場預報檢驗

PBL參數化過程對地面變量的預報有較大的影響。針對PBL參數化過程的集合預報方案對地面變量的預報結果是檢驗該方案優劣程度的重要指標。圖5是不同方案在研究時段內對2 m溫度和10 m風場預報的集合平均。其中圖中“CTRL”是控制實驗與觀測的偏差，其他圖為各個集合預報方案與控制實驗的偏差。從圖中可以看出，控制實驗對溫度的預報誤差，主要在陸面上表現出較大的暖偏差，大部分地區有1～2°的暖偏差，部分地區，特別是高原地區可以達到5°以上。這和他人研究WRF模式對夏季地面溫度的預報的結果類似。

首先，參數擾動的兩個實驗（PBL_brcrsb、PBL_pfac）對2 m溫度及10 m風場的預報無明顯改善作用，除了在高海拔地區有約0.01 ℃溫度變化外，其他地區幾乎沒有發生變化。而MULTI實驗。對2m溫度的預報改善作用主要在中國南部、緬甸、泰國等地，多物理方案可以降低上述地區0.2～0.3 ℃的暖偏差，雖然在中西部地區有0.1～0.2 ℃的增溫，但該方案讓整個區域平均降低0.017 ℃的暖偏差。同時該方案對風場的預報上，特別是在海上，有一定的改善作用。其次，傳統的SPPT方案，在格點方差η取較小值的MSPPT實驗，改善不明顯。但在提高了格點方差η的MSPPT5實驗中，該方案對整個模擬區域都有降溫作用，平均修正暖偏差約0.028 ℃，超過MULTI實驗。最后，針對PBL傾向的擾動方案，在取較大格點方差η的SPPBLPT5實驗中，展現了對暖偏差較大的修正作用。特別是模擬區域的南部，降溫作用高達0.5 ℃以上。雖然在青藏高原南部等部分地區，有0.1 ℃增溫，但該方案對模擬區域可以修正0.08 ℃的暖偏差，效果較好。同時該方案對風場，尤其是海上的10 m風場的改善作用也相當明顯。

為了驗證集合預報的效果，本文使用BS評分及其分解對2 m溫度和10 m風場的預報進行評估。如圖6所示。因為BS評分及可靠性評分（reliability）越小越好，可分辨性評分（resolution）越大越好，為了便于分析，圖6將BS及可靠性Y軸倒置。即靠上方的曲線預報效果比較好。從圖中可以發現，PBL_brcrsb、PBL_pfac實驗對溫度和風場的預報提高作用不顯著，但是相對的PBL_pfac實驗要比PBL_brcrsb略有提升。MSPPT5實驗表明傳統的SPPT方案可以改善集合預報系統對溫度和風場的概率預報性能，尤其是模式積分24～27 h對溫度，和模式積分時間21～36 h對風場的預報效果提升顯著。MULTI實驗在2 m溫度預報上有所提升，特別是模式積分的12、24和27 h有顯著提升。在風場預報上該方案在所有檢驗時段內，對比控制實驗均有顯著提高（評分顯著降低）。且隨著積分時間的增長，預報效果越好。MULTI實驗BS評分降低的主要原因是可靠性評分的降低，說明MULTI對溫度可能性的預報效果提升是該方案對集合預報系統性能提升的主要原因，而可分辨性并無明顯改變，說明多種PBL參數化方案對事件預報與觀測平均差異并不明顯。

但該方案的概率預報性能要略高于傳統SPPT方案。而SPPBLPT5實驗對2 m溫度和10 m風場的可能性預報提升明顯，除了模式積分時間15～21 h對溫度的預報性能提升不顯著以外，其他時段，以及所有時段對風場的概率預報，均有顯著的提升。從BS分解來看，該方案對可靠性的提升顯著，但對溫度預報的可分辨率在模式積分時間15～21 h的降低導致BS評分在該時段內，對集合預報系統性能提升并不顯著的主要原因。

從不同集合預報方案對地面溫度風場預報檢驗可以看出，SPPBLPT方案比傳統的SPPT方案可以更顯著的降低溫度預報的暖偏差，降低風場預報的誤差，提升集合預報系統對2 m溫度和10 m風場的預報性能。較大的格點方差η對預報改善作用更明顯。傳統的參數擾動對溫度與風場的預報提升性能有限，而多參數過程擾動雖然對預報有一定的改善，但并沒有SPPBLPT5實驗改善顯著。綜上所述，SPPBLPT5實驗對溫度與風場預報效果最好。

4.2 降水的預報檢驗

PBL方案對降水有較為顯著的影響。故本文考察不同集合預報方案對降水預報能力的提高，以檢驗SPPBLPT方案對集合預報系統中降水的改善作用。圖7是控制實驗對降水的預報RMSE，及其他集合預報方案的RMSE與控制實驗的差異。負值（紅色）代表該方案對降水預報有所提升，正值（綠色）代表該方案增加了降水預報的誤差。從控制實驗的RMSE可以看出，本文使用的WRF集合預報系統對研究時段的降水預報在海上及中國中南部等地誤差較大。

從圖中可以看出，對brcrsb參數的擾動對集合預報系統帶來的降水影響基本上可以忽略不計，對pfac參數進行擾動時，其對海面上降水的預報有所改變，但參數擾動的兩個實驗（PBL_brcrsb、PBL_pfac）對降水預報的影響都相對較小。MULTI實驗雖然對海上部分地區及越南地區對降水的預報有所改善，但總區域的降水改善甚微，總RMSE僅僅下降了0.002。SPPT方案對降水預報并沒有改善，MSPPT實驗與MSPPT5實驗表明，格點方差η越大，SPPT方案對降水預報效果越差。而SPPBLPT5實驗顯著地降低了降水預報的誤差，在沿海地區，該實驗對降水的RMSE改善能達到0.1～0.2。在海上，特別是沿臺風路徑和靠近模式邊界的海面上，該實驗能降低降水預報的RMSE高達0.5～1.0。該方案對整個區域的降水RMSE能改善0.05左右，在所有實驗中，SPPBLPT5實驗對降水的改善作用最為明顯。在降水改善較大的南部沿海地區，尤其是孟加拉灣地區，SPPBLPT5實驗顯著改善了風場的誤差，這也是導致降水預報RMSE降低的原因之一。

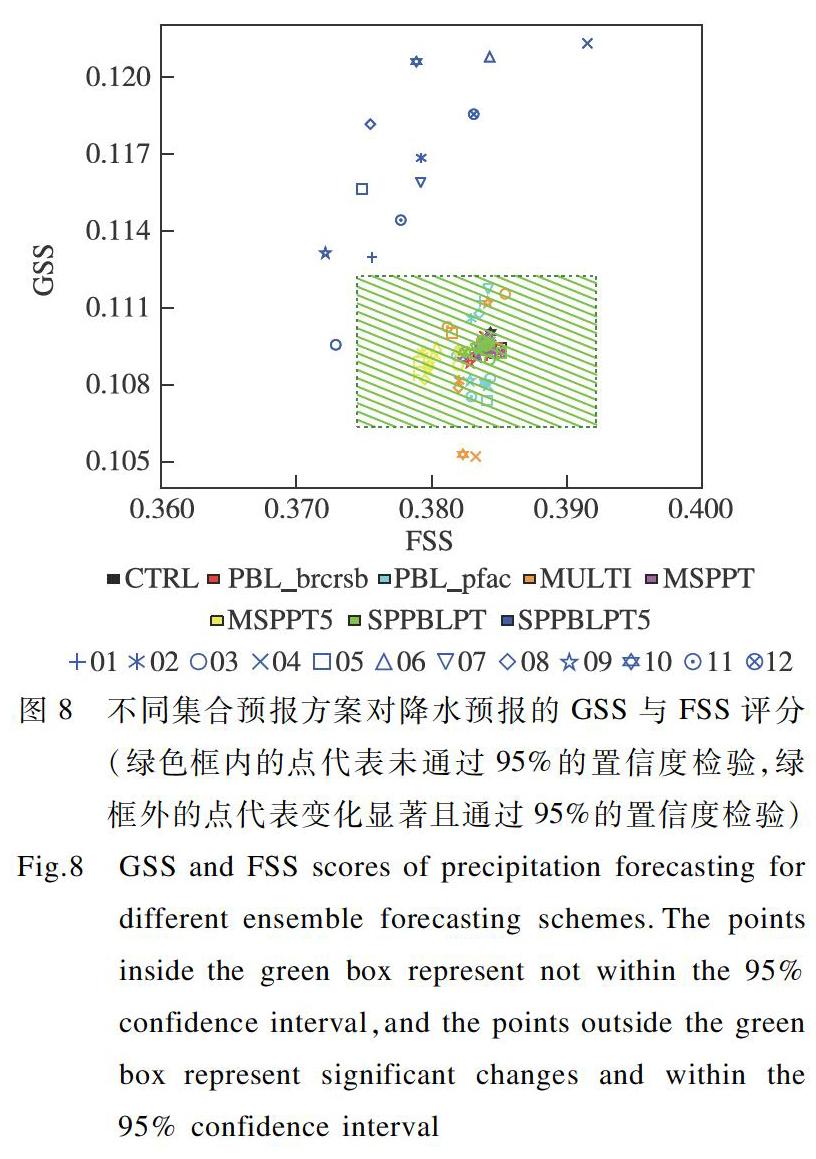
圖8為不同集合預報方案中每個成員對降水預報的GSS與FSS評分。圖中綠色陰影為變化不顯著區域，超出此區域的評分表明變化顯著。由圖可以看出，只有SPPBLPT5實驗對降水的GSS評分有顯著變化，除了3號成員的GSS評分沒有顯著變化外，其他11個成員對GSS評分都有顯著的提升。MULTI中4、10成員組GSS評分顯著降低，其他成員的變化并不顯著。其中3、9號成員組與5、11號成員組評分與控制實驗相比少許提升。但是在FSS評分上，各種集合預報方案都在不同程度上降低了該評分，SPPBLPT5僅僅有兩個成員顯著降低了FSS評分，其他成員對FSS的改變不明顯。FSS評分降低的現象與Li et al.（2020）的研究結果中出現的FSS降低現象類似。綜合來說，SPPBLPT5實驗對降水預報改善明顯。

5 結論

針對PBL參數化過程對集合預報系統帶來的誤差，在WRF模式中使用一種針對PBL參數化過程傾向的隨機物理過程擾動方案SPPBLPT，并利用該方案對2014年7月的地面溫度、風場、降水預報進行評估和對比，結論如下：

1）直接擾動PBL參數化過程傾向項比擾動所有參數化過程的總傾向項要有效，SPPBLPT方案與傳統的SPPT方案相比，對集合預報系統改善明顯。

2）SPPBLPT方案的性能受該方案中格點方差η參數的影響。較大的η值能顯著改善控制實驗中地面溫度的暖偏差，減少風場的預報偏差，降低降水預報的RMSE，提高預報系統的性能。

3）多PBL參數化過程擾動方案（MULTI實驗）可以在一定程度上降低溫度、風場、降水預報的誤差，但是受到具體PBL方案組合的影響很大，多參數化擾動方案（PBL_brcrsb、PBL_pfac實驗）說明擾動較敏感的參數，對預報的改變稍大，但總的來說，擾動PBL參數值的方法對預報效果的改變不顯著。這些方案都存在著選擇的主觀性，同時維護多種方案在業務上比較困難，相對而言，SPPBLPT方案有預報效果好、選擇客觀、維護簡便的優勢。

4）本文中，SPPBLPT方案的擾動參數相關時間τ，去相關尺度κ是使用前人的經驗取值，但這些參數對SPPBLPT性能的影響還需要進一步的探究。

參考文獻（References）

Berner J，Fossell K R，Ha S Y，et al.，2015.Increasing the skill of probabilistic forecasts：understanding performance improvements from model-error representations[J].Mon Wea Rev，143（4）：1295-1320.doi：10.1175/mwr-d-14-00091.1.

Bowler N E，Mylne K R，2009.Ensemble transform Kalman filter perturbations for a regional ensemble prediction system[J].Quart J Roy Meteor Soc，135（640）：757-766.doi：10.1002/qj.404.

Chen F，Dudhia J，2001.Coupling an advanced land surface-hydrology model with the Penn state-NCAR MM5 modeling system.part Ⅰ：model implementation and sensitivity[J].Mon Wea Rev，129（4）：569-585.doi：10.1175/1520-0493（2001）129<0569：caalsh>2.0.co;2.

陳浩，陳靜，汪矯陽，等，2017.觀測誤差對GRAPES區域集合預報影響的敏感性試驗[J].大氣科學學報，40（2）：193-201. Chen H，Chen J，Wang J Y，et al.，2017.Sensitivity tests of the influence of observation mean square error on GRAPES regional ensemble prediction[J].Trans Atmos Sci，40（2）：193-201.doi：10.13878/j.cnki.dqkxxb.20151102001.（in Chinese）.

陳靜，薛紀善，顏宏，2005.一種新型的中尺度暴雨集合預報初值擾動方法研究[J].大氣科學，29（5）：717-726. Chen J，Xue J S，Yan H，2005.A new initial perturbation method of ensemble mesoscale heavy rain prediction[J].Chin J Atmos Sci，29（5）：717-726.（in Chinese）.

陳耀登，王元兵，閔錦忠，等，2014.一種控制變量循環擾動和多參數化方案的混合同化方法[J].大氣科學學報，37（6）：732-739. Chen Y D，Wang Y B，Min J Z，et al.，2014.A hybrid assimilation method with control variable cycle perturbation and multi-physical parameterization[J].Trans Atmos Sci，37（6）：732-739.doi：10.13878/j.cnki.dqkxxb.20130923007.（in Chinese）.

Christensen H M，Moroz I M，Palmer T N，2015.Stochastic and perturbed parameter representations of model uncertainty in convection parameterization[J].J Atmos Sci，72（6）：2525-2544.doi：10.1175/jas-d-14-0250.1.

Cohen A E，Cavallo S M，Coniglio M C，et al.，2015.A review of planetary boundary layer parameterization schemes and their sensitivity in simulating southeastern US cold season severe weather environments[J].Wea Forecasting，30（3）：591-612.doi：10.1175/waf-d-14-00105.1.

代昕鷺，陳葆德，張旭，等，2017.WARMS 2.0中邊界層參數化方案對一次臺風外圍降水模擬預報的影響[J].成都信息工程大學學報，32（5）：513-523. Dai X L，Chen B D，Zhang X，et al.，2017.Impact of different boundary layer parameterization schemes on the numerical smiulation for a typhoon rain event in WARMS 2.0[J].J Chengdu Univ Inf Technol，32（5）：513-523.doi：10.16836/j.cnki.jcuit.2017.05.009.（in Chinese）.

狄靖月，趙琳娜，張國平，等，2013.降水集合預報集成方法研究[J].氣象，39（6）：691-698. Di J Y，Zhao L N，Zhang G P，et al.，2013.Study on precipitation multimodel super ensemble forecast technique[J].Meteor Mon，39（6）：691-698.doi：10.7519/j.issn.1000-0526.2013.06.004.（in Chinese）.

Di Z H，Duan Q Y，Gong W，et al.，2015.Assessing WRF model parameter sensitivity：a case study with 5 day summer precipitation forecasting in the Greater Beijing Area[J].Geophys Res Lett，42（2）：579-587.doi：10.1002/2014gl061623.

杜鈞，2002.集合預報的現狀和前景[J].應用氣象學報，13（1）：16-28. Du J，2002.Present situation and prospects of ensemble numerical prediction[J].J Appl Meteor Sci，13（1）：16-28.doi：10.3969/j.issn.1001-7313.2002.01.002.（in Chinese）.

Duc L，Saito K，Seko H，2013.Spatial-temporal fractions verification for high-resolution ensemble forecasts[J].Tellus A：Dyn Meteorol Oceanogr，65（1）：18171.doi：10.3402/tellusa.v65i0.18171.

Hamill T M，1999.Hypothesis tests for evaluating numerical precipitation forecasts[J].Wea Forecasting，14（2）：155-167.doi：10.1175/1520-0434（1999）014<0155：htfenp>2.0.co;2.

Hariprasad K B R R，Srinivas C V，Singh A B，et al.，2014.Numerical simulation and intercomparison of boundary layer structure with different PBL schemes in WRF using experimental observations at a tropical site[J].Atmos Res，145/146：27-44.doi：10.1016/j.atmosres.2014.03.023.

Lamraoui F，Booth J F，Naud C M，et al.，2019.The interaction between boundary layer and convection schemes in a WRF simulation of post cold frontal clouds over the ARM east north Atlantic site[J].J Geophys Res Atmos，124（8）：4699-4721.doi：10.1029/2018jd029370.

Li C H，Berner J，Hong J S，et al.，2020.The Taiwan WRF ensemble prediction system：scientific description，model-error representation and performance results[J].Asia-Pac J Atmos Sci，56（1）：1-15.doi：10.1007/s13143-019-00127-8.

Li X，He H R，Chen C H，et al.，2017.A convection-allowing ensemble forecast based on the breeding growth mode and associated optimization of precipitation forecast[J].J Meteor Res，31（5）：955-964.doi：10.1007/s13351-017-6695-0.

Li X L，Pu Z X，2008.Sensitivity of numerical simulation of early rapid intensification of hurricane emily （2005） to cloud microphysical and planetary boundary layer parameterizations[J].Mon Wea Rev，136（12）：4819-4838.doi：10.1175/2008mwr2366.1.

李曉莉，陳靜，劉永柱，等，2019.GRAPES全球集合預報初始條件及模式物理過程不確定性方法研究[J].大氣科學學報，42（3）：348-359. Li X L，Chen J，Liu Y Z，et al.，2019.Representations of initial uncertainty and model uncertainty of GRAPES global ensemble forecasting[J].Trans Atmos Sci，42（3）：348-359.doi：10.13878/j.cnki.dqkxxb.20190318001.（in Chinese）.

閔錦忠，房麗娟，2017.基于增長模繁殖法的暴雨集合預報[J].大氣科學學報，40（1）：1-12. Min J Z，Fang L J，2017.Storm ensemble forecast based on the BGM method[J].Trans Atmos Sci，40（1）：1-12.doi：10.13878/j.cnki.dqkxxb.20140404002.（in Chinese）.

潘留杰，張宏芳，陳小婷，等，2015.基于鄰域法的高分辨率模式降水的預報能力分析[J].熱帶氣象學報，31（5）：632-642. Pan L J，Zhang H F，Chen X T，et al.，2015.Neighborhood-based precipitation forecasting capability analysis of high-resolution models[J].J Trop Meteor，31（5）：632-642.doi：10.16032/j.issn.1004-4965.2015.05.006.（in Chinese）.

Pleim J E，2007.A combined local and nonlocal closure model for the atmospheric boundary layer.part I：model description and testing[J].J Appl Meteorol Climatol，46（9）：1383-1395.doi：10.1175/jam2539.1.

Romine G S，Schwartz C S，Berner J，et al.，2014.Representing forecast error in a convection-permitting ensemble system[J].Mon Wea Rev，142（12）：4519-4541.doi：10.1175/mwr-d-14-00100.1.

Wang Y，Bellus M，Wittmann C，et al.，2011.The Central European limited-area ensemble forecasting system：ALADIN-LAEF[J].Quart J Roy Meteor Soc，137（655）：483-502.doi：10.1002/qj.751.

吳增茂，張新玲，2000.大氣系統集合預報方法及應用研究的發展[J].氣象科技，28（1）：16-20，26. Wu Z M，Zhang X L，2000.The developmet of ensemble forecasting method and its application in atmospheric system[J].Meteror Sci Technol，28（1）：16-20，26.doi：10.19517/j.1671-6345.2000.01.002.（in Chinese）.

朱躍建，2020.基于最新全球集合預報系統的可預報性評估[J].大氣科學學報，43（1）：193-200. Zhu Y J，2020.An assessment of predictability through state-of-the-art global ensemble forecast system[J].Trans Atmos Sci，43（1）：193-200.doi：10.13878/j.cnki.dqkxxb.20191101013.（in Chinese）.

In this study，targeted at the uncertainty in the parameterization process of the planetary boundary layer in the WRF model，a Stochastic Perturbation on Planetary Boundary Layer Parameterization Tendency scheme （SPPBLPT） was developed.This scheme perturbs the temperature，wind and water vapor tendencies.A comparative experiment was conducted in July 2014 using the SPPBLPT scheme，multi-planet boundary layer parameterization scheme，multi-parameter perturbation scheme，and Stochastic Physical Process Perturbation （SPPT） scheme.It was observed that the SPPBLPT scheme with a large grid-point variance can effectively reduce the error of 2 m temperature and wind field，and it can also reduce precipitation error，while other schemes do not improve the forecast significantly.The BS scores for the 2 m temperature and wind field show that the SPPBLPT scheme significantly improves the possibility of ensemble forecasting for temperature and wind field，by reducing the reliability score，thereby increasing performance.At the same time，the scheme can significantly improve the GSS score of the precipitation.In all experiments，the SPPBLPT scheme with the larger grid-point variance had a superior performance.Although the SPPBLPT scheme reduced the FSS score，the reduction was not significant.It is thus shown that the SPPBLPT scheme can significantly improve the performance of ensemble forecasting systems，yet the setting of perturbation parameters for this scheme requires further investigation.

PBL;stochastic perturbation;ensemble forecast;WRF model

doi：10.13878/j.cnki.dqkxxb.20191223001

（責任編輯：袁東敏）