農業機械作業大數據清洗方法與試驗優化

苑嚴偉 徐 玲 冀福華 郭大方 安 颯 牛 康

(中國農業機械化科學研究院土壤植物機器系統技術國家重點實驗室， 北京 100083)

0 引言

農機大數據平臺建設是推進現代農業生產信息化、智能化、精準化的重要環節[1-7]。隨著北斗系統、5G通信、物聯網等技術迅速發展，大數據平臺不斷完善，入網農機數量猛增，數據規模不足問題得到緩解，但數據質量問題成為阻礙平臺發展的新瓶頸。據統計，大型數據集中的錯誤率約為5%[8]。數據清洗能夠減少“Garbage in, garbage out”現象，但所需時間很長，一般約占數據分析總時間的60%～80%[9-10]。準確高效的數據清洗方法能夠提高平臺分析決策的可靠性和時效性，是農機大數據平臺發展的重要基石。

國內外關于數據清洗的研究主要集中在異常數據檢測[11-17]方面，對異常數據修復的研究較少。處理異常數據的傳統方式有直接保留、刪除和人工填充等，其效果不夠理想。ETL(Extract transform load)工具雖然能夠實現數據抽取、轉換和加載，但是修復能力較弱，不能滿足應用需求。文獻[18]針對工業大數據中的高維時間序列數據，基于領域知識支持，開發了在線與離線相結合的數據清洗系統Cleanits。文獻[19]針對時間序列異常數據修復問題，提出將時間相關特性與最小變動原理相結合的IMR(Iterative minimum repairing)框架。文獻[20]針對平滑過濾方法嚴重更改原始數據、且已有算法不支持流數據計算的問題，提出利用數據浮動速度函數修復高度異常數據的方法。文獻[21-23]利用Spark分布式計算框架加快了大數據清洗流程。目前，已有數據清洗算法均未充分利用數據間的相互關系，對原始數據改動大，不適用于具有大規模、多源異構、高維度、強時空相關等特點的農機實時流數據。

為此，本文分析數據異常出現的主要場景及原因，根據農機作業數據的時間相關性和最小變動原則，提出一種數據清洗方法，依托Flink流計算平臺實現數據的實時分析，通過試驗驗證算法的有效性，并對算法進行試驗優化。

1 復雜作業條件下數據異常分析

由于應用領域存在差異，數據異常的概念缺乏統一定義。本文將數據異常定義為：在某一瞬時，服務器接收到的數據(或數據的某一部分)出現不完整、不準確、不合法等現象。

田間作業條件復雜，增加了數據異常發生的概率。在實際工作中，易發生數據異常的主要場景如下：

(1)田間環境影響傳感器檢測精度。例如，地塊周圍存在高大樹木或建筑物等，會遮擋一些傳感器(如衛星定位傳感器)的信號，導致數據出現跳變、離散或缺失。

(2)作業工況影響傳感器檢測精度。例如，作業過程中土壤或谷物產生的粉塵會干擾傳感器(如光學傳感器)的敏感元件；地面不平整或機器運轉產生的振動也會影響傳感器(如沖量式測產傳感器)的檢測精度，導致數據出現異常。該類型數據異常具體表現為數據出現零散、漂移或抖動。

(3)農機自身因素影響傳感器檢測精度。例如，機器的發動機或供電系統工作不穩定，引起電壓波動，導致傳感器(如電容式傳感器)的檢測性能隨電壓波動。該類型數據異常具體表現為數據出現漂移、丟失或抖動。

(4)田間環境影響信息上傳質量。例如，田間網絡信號差或存在電磁干擾，會影響數據傳送的時效性和準確性，導致數據出現延時或缺失。

本文所討論的數據異常不包括作業環境合理變化導致的數據波動。例如：在同一地塊中，由于土壤肥力不同導致農作物產量變化，盡管數據看起來比較反常，但是并不屬于異常數據。

2 基于滑動窗口的數據在線清洗算法

為實現數據在線清洗，提出基于滑動窗口實現的流數據異常識別和修復算法。針對農機作業數據以數值型為主的特點，基于方差約束原則識別異常數據；基于最小變動原則，對異常數據的原始值進行初步估算，生成候選數據；根據數據時間相關性，基于AR(Autoregressive model)、ARX(Autoregressive model with exogenous input)模型得到最優修復值。因此，算法分為識別異常數據、生成候選修正數據、數據迭代修正3個步驟，如圖1所示。

2.1 異常數據動態識別

在每個數據對應的窗口區間內，進行方差檢驗，評估其是否為異常。通過窗口的滑動，可以依次評估每個數據，實現數據流的動態異常識別。

假設原始數據集Γ內前w個數據可靠，對于Γ內第i(i=w,w+1,w+2,…)個數據γi，選取大小為w的窗口Di={di1,di2,…,diw}，其中dij=γi-w+j，則Di的方差為

(1)

式中dij—— 窗口Di中第j個數據

依據以往所采集的同類數據的方差v′，選取方差閾值v作為評判基準，v的取值應略大于v′，即v=λv′，其中λ為按經驗選取的大于1的常數。當δ(Di)≤v時，則γi為正常數據；當δ(Di)>v時，則γi為異常數據。

若γi為正常數據，則窗口向后滑動，對第i+1個數據γi+1進行評估。若γi為異常數據，則修復該數據后，再向后滑動窗口。

2.2 異常數據候選修正集生成

若確定γi為異常數據，則設其為x，并令δ(Di)=v，2個原始解x1和x2求解公式為

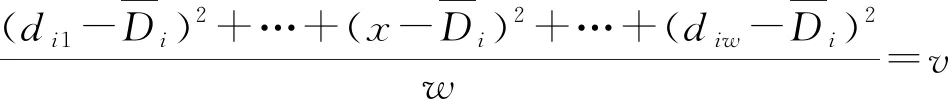
(2)

假設x1≤x2，對于異常數據γi，必然有γix2。當γix2時，γ′i取x2。候選數據γ′i，即

(3)

通過此方法，依次將所有異常數據替換為候選數據，生成候選數據集Γ′。

2.3 候選修正集迭代優化

由于生成候選數據集的方法較為粗放，因此引入AR和ARX模型，利用異常數據γi前面m個數據，對γi的候選值γ′i進行優化，保證數據修正準確可靠。

若m個數據均為正常數據，則使用AR模型更新候選數據γ′i，得到最終修復值為

(4)

C——常量m——階數

φk——AR、ARX模型參數

εi——白噪聲點

否則，使用ARX模型對第i-m個至第i-1個數據的原始值與候選值的差加權求和，更新候選數據γ′i，得到最終修復值為

(5)

其中φk、m可利用數學統計進行估算。樣本數據集Γ的協方差函數符合Yule-Walker方程，可以得到

(6)

式中β0、β1、…、βp——Γ的協方差函數

轉換為矩陣形式

Apφ(p)=Bp

(7)

由于矩陣Ap對稱且可逆，因此可得

(8)

此時，可以求出φk，其中φ(p)的第p個分量φpp，即為偏相關函數。

根據AR(m)的特性可知，其偏自相函數m步截尾(在大于某個常數后快速趨于0)，因此可以將點(p，φpp)在笛卡爾坐標系中標出。當存在某個p之后，φpp無限接近0，此時的p即為所求的階數m。執行迭代，直至前后2次迭代的γ′i小于閾值τ時，停止迭代。

數據異常清洗算法步驟如下：

(1)輸入Γ、v、w、τ

(2)處理γi

γi→Di

ifδ(Di)≤v

else

forlto …

δ(Di)=v→x1,x2(x1≤x2)

ifγi≤x1

γ′i,0=x1

else

γ′i,0=x2

end

ifγi-m,…,γi-1do not have abnomal data

else

break

end

end

end

end

(3)輸出Γ*

3 試驗與分析

3.1 試驗材料

在現有農機大數據平臺中，選取2016—2019年某省農機深松、保護性耕作等8種類型的作業數據，規模大于1×109條，代表性字段如表1所示。

表1 農機數據基本信息

為適應農機作業數據吞吐量大、并發度高的特點，將算法遷移至大數據流計算平臺Flink上，依托Flink集群的分布式特性，保證算法快速準確執行。傳感器通過TCP/IP協議將海量數據傳輸至Kafka集群進行分組管理。然后，Flink消費者集群接收數據并運行算法，實現流數據清洗。系統部署在阿里云服務器上，相關配置如表2所示。

表2 試驗環境

3.2 算法有效性驗證

3.2.1驗證方法

算法有效性包括異常數據識別有效性和修復有效性。使用精確率P1、召回率R和綜合性指標F1評價異常數據識別有效性。使用均方根誤差ERMSE評價數據修復有效性，計算式為

(9)

式中n——異常數據個數

算法有效性驗證方案流程如圖2所示。首先，選取一定規模的正常數據，并人工對其進行預處理，將一定比例的正常數據修改至異常，同時標記正常數據為1，異常數據為0。將預處理后的數據作為試驗集，使用算法完成數據清洗。進行多次清洗后，取各評價指標的平均值進行分析。

為更加具體地展現本算法的修復效果，采用基于平滑的清洗算法SWAB[24]和基于否定約束的全局清洗算法Holistic[25]與本算法進行橫向對比。

3.2.2驗證結果

(1)選取不同規模的試驗集，在數據預處理時將5%的數據修改至異常，取窗口大小為100，階數取值為4，閾值取值為0.1。在每一規模水平下進行3次試驗，分別對P1、R、F1和ERMSE取平均值。

如圖3所示，P1、F1隨數據量增加而增大。當數據規模達到1×105條，P1在0.94附近趨于穩定；R一直處于0.9～0.95區間內；F1大于0.92。說明算法在大規模數據集中具有較高的異常識別率。

均方根誤差隨數據規模的變化如圖4所示。隨著數據規模的增大，3種算法的均方根誤差均減小，且在數據達到一定規模后，均方根誤差的變化趨緩。SWAB算法均方根誤差始終較高。在數據規模小于1×105條時，Holistic與本文算法表現相近，但在數據規模大于等于1×105條時，后者的均方根誤差明顯更小，表明本文算法修復效果較好。

(2)選取規模為1×105條的試驗集，在窗口大小為100、階數為4、閾值為0.1時，選取不同數據異常率進行試驗。試驗結果如圖5所示，同一數據規模下，3種算法的均方根誤差均隨數據異常率的增大而增大，SWAB算法最高，Holistic算法次高，本文算法始終最低，說明所提出的算法在修復準確性方面有效，且數據異常率越低表現越好。

3.3 算法試驗優化

由前述分析，數據規模處于較高水平、錯誤率處于較低水平時，二者對均方根誤差的影響很小，并且實際情況中數據規模與錯誤率不可控。因此，對算法的優化主要考慮階數、閾值、窗口大小對均方根誤差ERMSE和算法運行時間T的影響。采用Box-Behnken原理設計試驗，各試驗因素編碼如表3所示，試驗設計與結果如表4所示，A、B、C為因素m、τ、w編碼值。

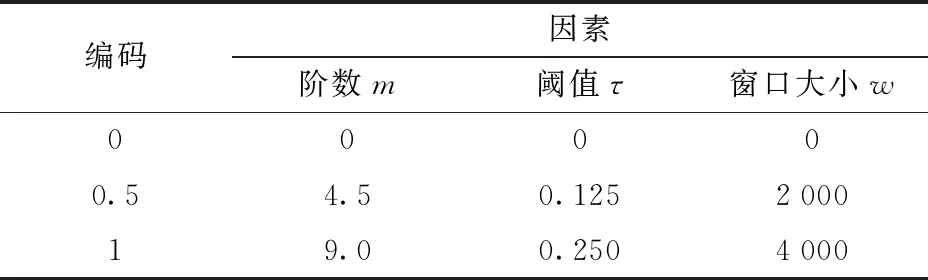
表3 因素編碼

對試驗結果進行分析，選擇回歸模型進行擬合。均方根誤差和算法運行時間的方差分析結果如表5、6所示，所建立的模型均顯著(P≤0.05)，且失擬項不顯著，證明模型所擬合的回歸方程與實際相符，能準確反映均方根誤差、時間與階數、閾值、窗口大小之間的關系。在保證模型可靠的前提下，為使回歸模型更好地對試驗結果進行預測，剔除不顯著項，對回歸模型做優化調整，分別得到ERMSE和T的回歸模型為

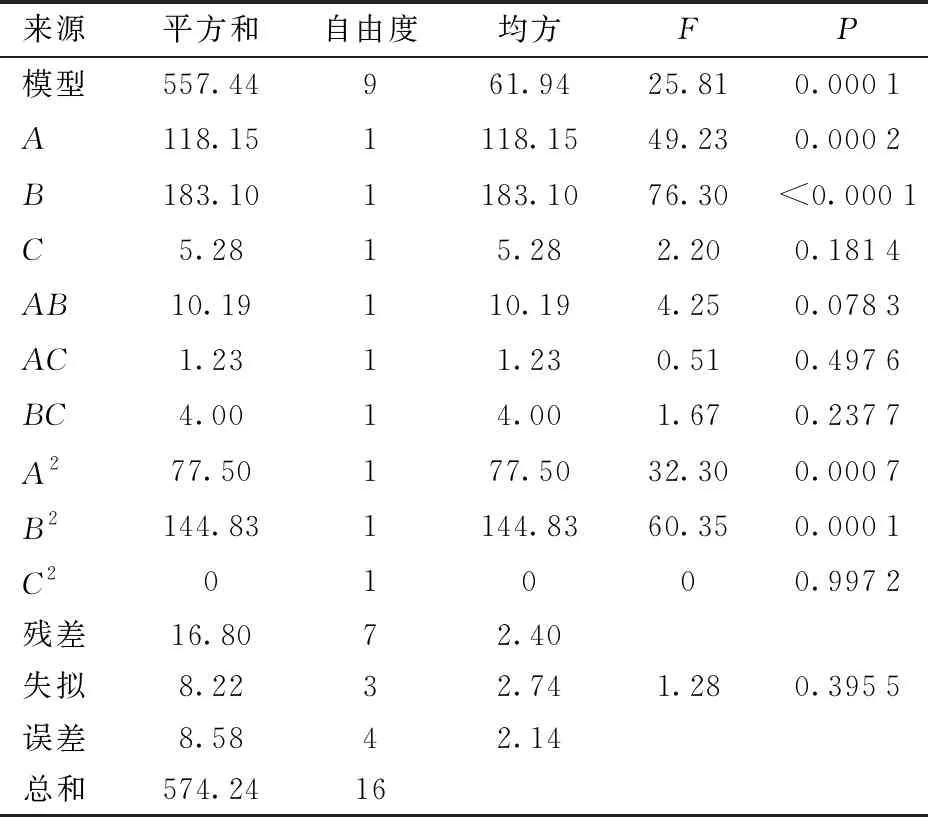
表5 均方根誤差ERMSE方差分析

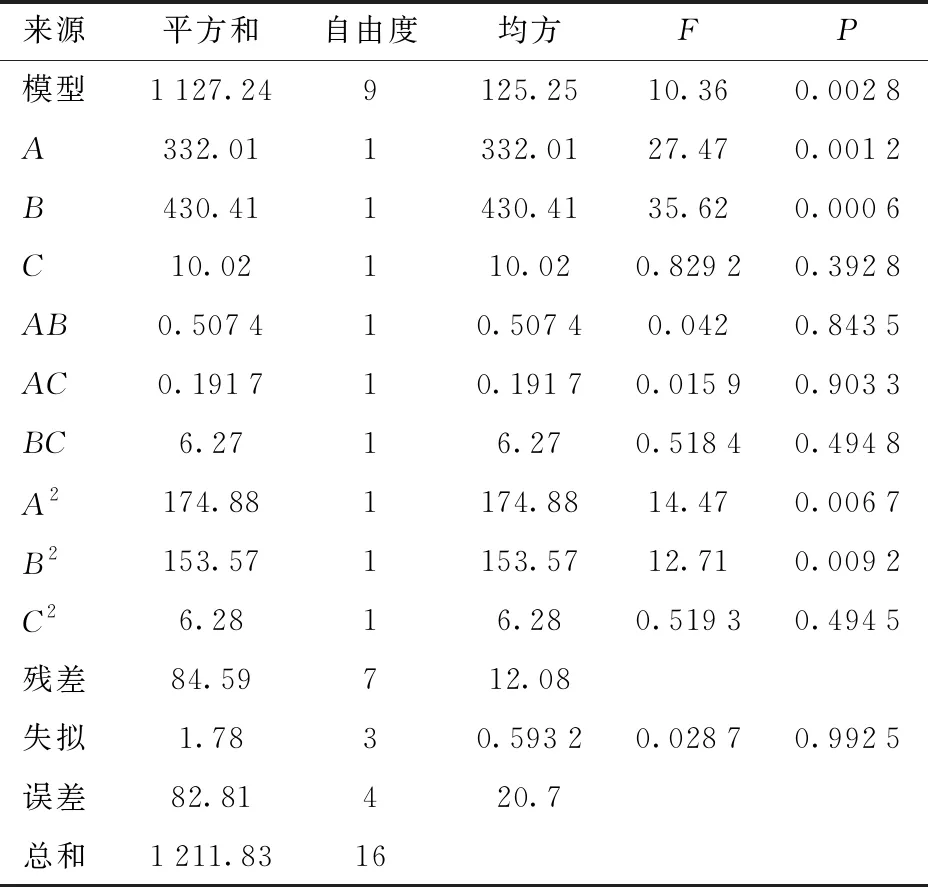
表6 算法運行時間T方差分析

ERMSE=11.28-24.85A-13.89B+17.16A2+23.46B2(A,B∈[0,1])

(10)

T=17.22-12.64A-38.57B+25.52A2+23.90B2(A,B∈[0,1])

(11)

將回歸模型映射回原空間可得

ERMSE=11.28-2.76m-55.56τ+0.21m2+375.36τ2(m∈[0,9],τ∈[0,0.25])

(12)

T=17.22-1.4m-154.28τ+0.32m2+382.4τ2(m∈[0,9],τ∈[0,0.25])

(13)

由圖6可以看出，當閾值τ一定時，隨著階數m的增大，均方根誤差先減少后增大。這說明過大的階數并不會持續增加算法的準確度。當階數一定時，均方根誤差隨閾值增大而增大，這說明選取較小的閾值能提高算法準確性。

由圖7可以看出，當階數一定時，隨著閾值逐漸變大，算法運行時間逐漸減少；當閾值較小時，需要較高的時間成本。當閾值一定時，算法運行時間隨階數增大而增大，結合階數對均方根誤差的影響，說明選取過大的階數導致算法準確性差且效率低。

云服務平臺使用目的不同，所要求的性能指標不同，有些注重數據準確性，有些更關注實時性。為此，本文采用二進制編碼的混合遺傳算法，分別對式(12)、(13)所示的模型進行優化求解，確定不同性能指標下的參數組合，優化過程如圖8、9所示。設定種群個體數目為15，交叉概率為0.8，變異概率為0.08。迭代求解得到，當階數為6.6，閾值為0.07時，均方根誤差最小為0.16；當階數為2，閾值為0.2，算法運行時間最小為0.13 s。

4 結論

(1)研究異常數據檢測及修正技術，提出一種基于滑動窗口機制的數據在線清洗算法，并依托Flink分布式計算平臺，加速數據的實時清洗，以適應農機大數據高并發、吞吐量大的特點。

(2)試驗表明，針對規模為1×105條、異常率為5%的數據集，算法窗口大小取100、階數取4、閾值取0.1時，精確率、召回率和綜合性指標均滿足數據清洗要求。與SWAB算法和Holistic算法修復后的均方根誤差的對比表明，本文算法的均方根誤差更小，從而證明了本文算法的有效性。本文算法的均方根誤差隨數據規模的增大而減小，隨數據異常率的增大而增大，說明該算法適用于異常率較低的大規模數據集。

(3)基于Box-Behnken原理設計試驗，分別建立均方根誤差、算法運行時間與階數、閾值、窗口大小之間的響應曲面回歸模型。利用基于二進制編碼的混合遺傳算法求出滿足各性能指標的多參數最優組合，當階數為6.6、閾值為0.07時，均方根誤差最小為0.16，當階數為2、閾值為0.2時，算法運行時間最短為0.13 s。