基于粒子群算法的增壓柴油機神經網絡模型

陳昊天，王玥，曹晶，張繼忠，鄧康耀，崔毅

(1.上海交通大學動力機械與工程教育部重點實驗室，上海 200240；2.上海核工程研究設計院有限公司，上海 200233；3.中國北方發動機研究所(天津)，天津 300400)

隨著計算機水平的提升，硬件在環技術(HIL)在發動機控制系統的開發中得到廣泛地應用。在HIL系統中，發動機仿真模型是一個重要的組成部分。為了能夠有效地實現HIL仿真，發動機仿真模型不僅需要滿足一定的精度，還需要滿足面向控制的要求，也就是要實現快速計算，滿足實時性約束[1-2]。

當前，應用于HIL系統的性能預測模型主要分為以下幾種：平均參數模型、曲軸轉角精度模型以及基于神經網絡的仿真模型[3]。Hendricks首次提出了平均值模型這一概念，不考慮參數在循環內的變化，只考慮循環間的變化，避免了十分復雜的工作過程[4]。雖然平均參數模型計算效率高，但是模型的精度不高，并且需要大量的數據進行標定[5]。曲軸轉角精度模型利用微分方程計算參數隨曲軸轉角的變化，因此精度較高[6]。雖然曲軸轉角模型預測能力較強，但是不能完全滿足計算速度的要求，尤其是對于高轉速的機型[7]。平均參數模型和曲軸轉角精度模型無論是基于Simulink建立或者是利用某種編程語言編寫，都需要較為復雜的前期開發工作。人工神經網絡在處理非線性問題上具有優勢，近年來在柴油機動力性、排放性以及性能模型建立等研究中得到廣泛的應用[8-10]。神經網絡模型是針對具體的發動機對象建立的，其通用性較差，但是在樣本滿足要求的情況下，神經網絡模型的建立和訓練較為簡單，使用方便。離線模型的計算速度很快，并且方便與Simulink中搭建的或者自主編程開發的控制系統耦合，在面向控制的模型建立問題上可以得到很好的應用。

BP神經網絡(Back-Propagation Neural Network)是一種按照誤差逆向傳播算法訓練的多層前饋神經網絡[11]，在柴油機研究中應用廣泛，但是其無法保證得到全局最優解，收斂速度和泛化能力較差，很難滿足精度上的需求[12]。因此，近年來對神經網絡開展了很多優化算法的研究，比如遺傳算法和群體智能算法等[13-14]。群體智能算法魯棒性較強，并且全局收斂能力好，與BP神經網絡結合，可以充分發揮雙方的優勢。

現有的發動機神經網絡模型主要用于分析穩態工況，對瞬態性能的預測精度、訓練速度以及泛化能力較差。因此，本研究選擇群體智能算法中的粒子群算法(PSO算法)，提出了預測柴油機全工況穩態及瞬態性能的通用神經網絡模型構建方法，并與傳統的BP神經網絡方法進行了全面的比較。

1 柴油機神經網絡模型的搭建

1.1 訓練樣本獲取

本研究所針對的柴油機為某型渦輪增壓中速柴油機，柴油機的具體參數如表1所示。

表1 柴油機主要參數

為了獲取神經網絡模型的訓練樣本，在該柴油機上開展了穩態和瞬態試驗。穩態試驗包括25%，50%，75%，90%，100%，110%六個穩態工況點的柴油機性能數據。瞬態試驗主要是變負荷試驗，當負荷變化時，轉速通過電子調速器進行PID調節。

由于穩態試驗下獲取的樣本數不足以對神經網絡模型進行充分的訓練，因此基于一維非定常流動計算方法，在發動機性能仿真軟件SPEED中建立柴油機計算模型(見圖1)，并利用試驗數據進行校核，結果見圖2。

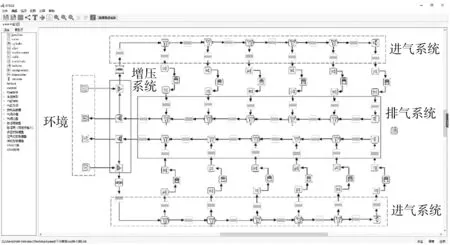
圖1 柴油機仿真模型

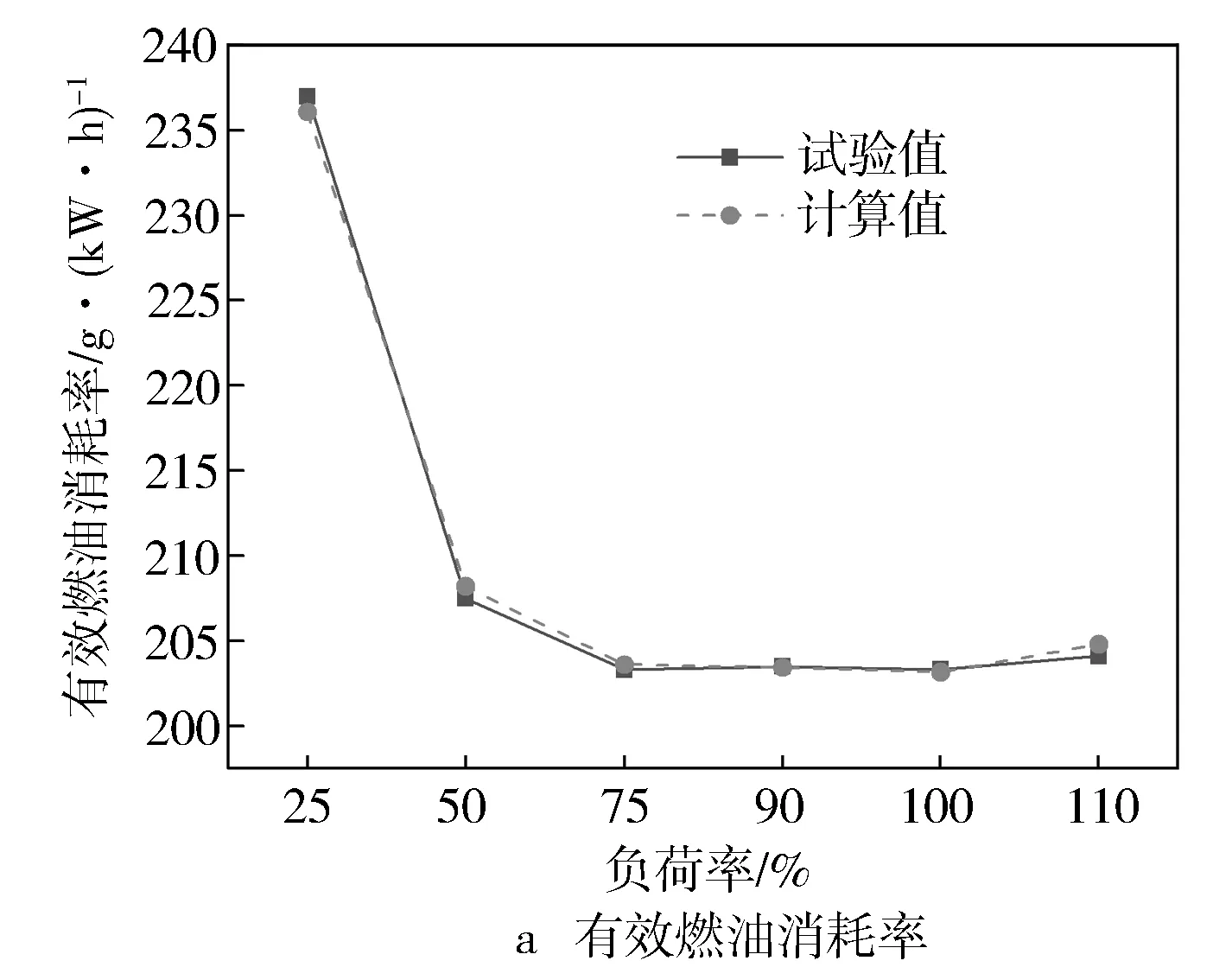
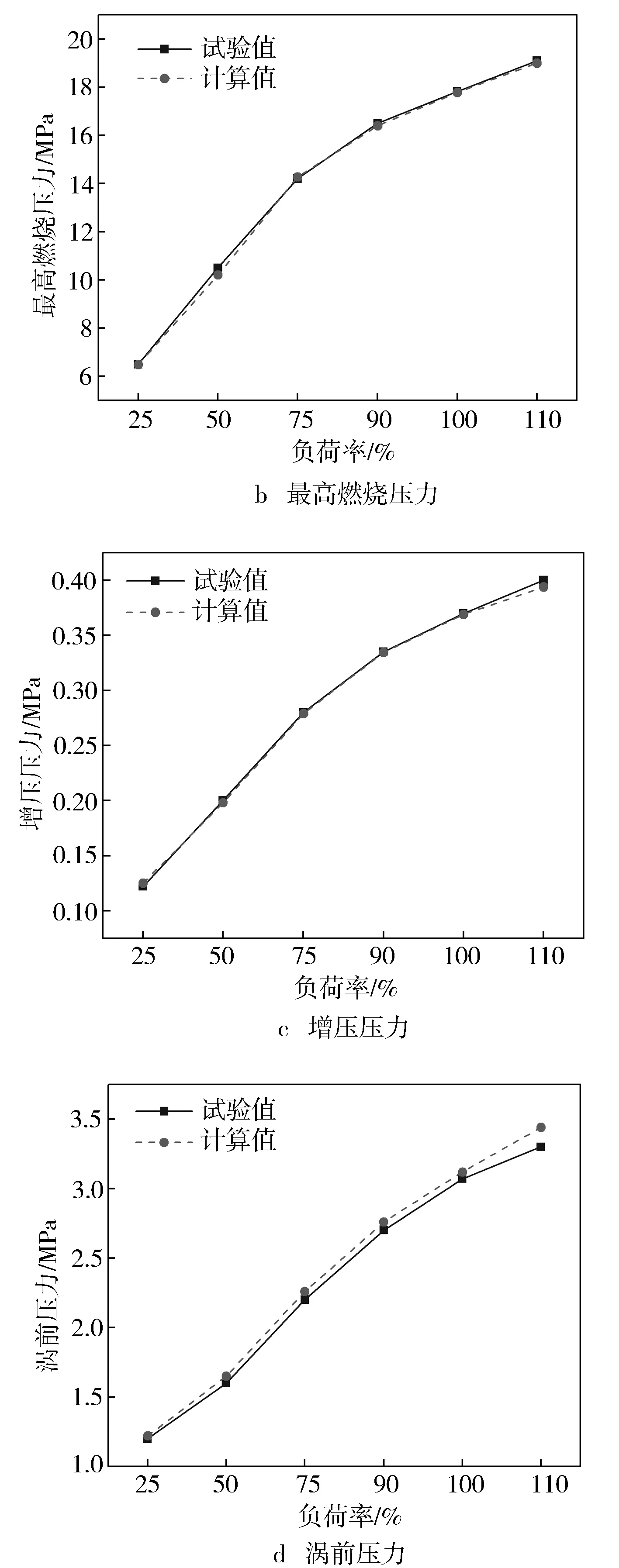
圖2 仿真模型精度校核結果

利用仿真模型進行不同轉速、負荷、噴油參數下的計算，變量范圍如表2所示，總共獲取穩態訓練樣本300組。瞬態訓練樣本主要包括定轉速下增減負荷導致的參數變動，考慮不同的負荷初值、負荷終值以及變化速率。為了盡可能使得訓練樣本覆蓋運行工況，本研究中瞬態樣本負荷變化范圍為10%～100%，選擇50%負荷作為起始值，變動時間范圍為2～30 s，如表3所示，總計42組樣本曲線。各個工況的計算時間均為75 s，負荷變化起始時刻均為30 s。

表2 穩態工況變量取值范圍

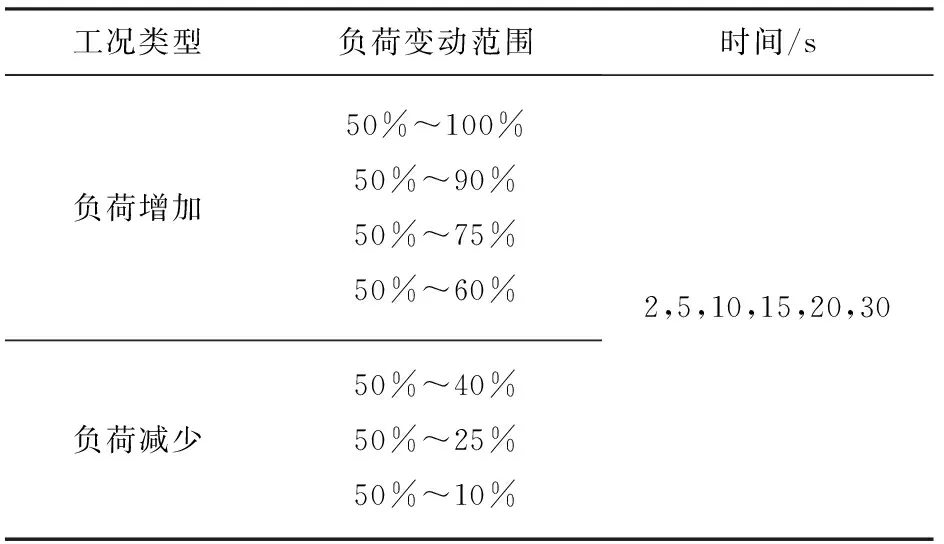
表3 瞬態工況負荷變化范圍

1.2 神經網絡結構

本研究建立的神經網絡模型輸入包括轉速、噴油量、噴油時刻、噴油量隨時間的變化率。前面三個輸入可以用于穩態性能模型的建立[14-16]，但是為了建立能夠對穩態和瞬態性能均可以有效預測的通用神經網絡模型，需要將噴油量變化率作為輸入，因為在瞬態工況下，負荷的變化加上調速器的PID調節導致噴油的變化，而噴油量變化率對輸出參數的變化趨勢有重要的影響。穩態工況的訓練不考慮噴油量隨時間的變化，因此樣本中噴油量的變化率為0。瞬態工況的訓練主要考慮定轉速變負荷，輸入參數中主要是噴油量及其變化率在起作用，樣本中轉速值設為標定轉速。

基于神經網絡的實時模型主要是面向控制的，輸出量主要考慮控制系統需要的主要性能參數，因此本研究選擇的模型輸出參數為增壓壓力、缸內最高燃燒壓力、排氣溫度和燃油消耗率。本研究所采用的神經網絡為BP神經網絡，網絡結構見圖3。

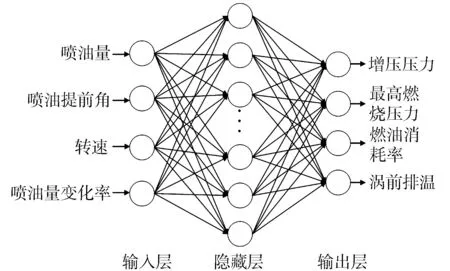
圖3 神經網絡結構

除了輸入層和輸出層外，該網絡還包含一層隱藏層，隱藏層的節點數對整個網絡的預測效果有十分重要的影響[17]。網絡的預測性能主要包括兩個指標，訓練樣本的學習效果以及測試樣本的泛化效果，這兩個指標是一對矛盾體。隱藏層節點數越多，學習效果越好，但是隱藏層節點過多，容易出現過擬合的現象，導致泛化效果較差[16]。因此，節點數的選取要適當。本研究采用試錯法來選擇隱藏層的節點數，通過均方誤差(MSE)來表征網絡的預測效果，不同個數的隱藏層節點下的MSE對比如圖4所示(取50次測試結果的平均值)。因此，本研究中選擇的模型隱藏層節點個數為10。

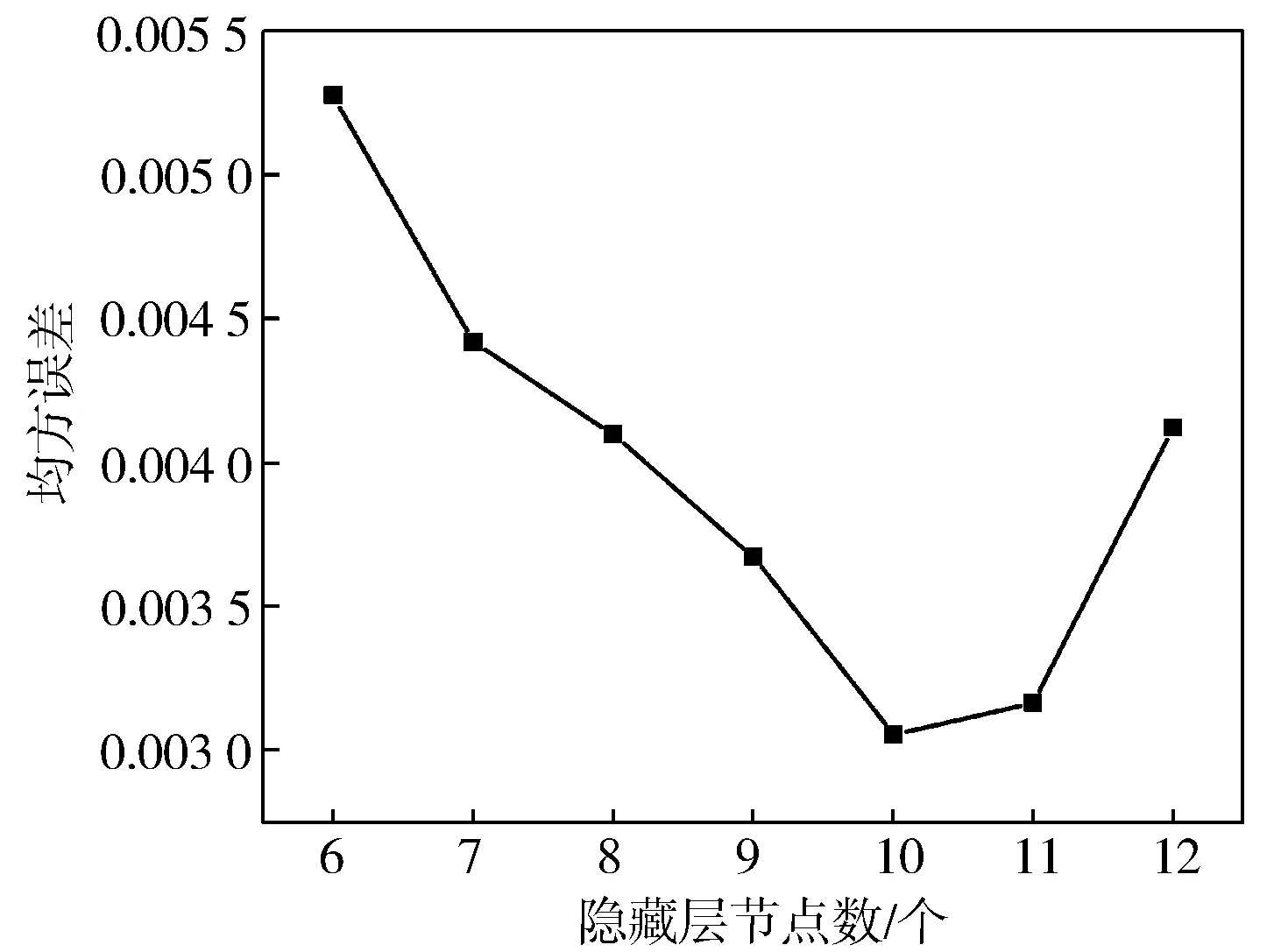
圖4 不同隱藏層節點下的均方誤差對比

1.3 網絡訓練

本研究使用Matlab中的神經網絡工具進行建模，由于輸入輸出數據在數量級上會有較大的差別，數量級較小的參數對網絡權值的影響有可能會被忽略，從而影響網絡的訓練和預測精度，因此要對樣本進行歸一化處理。

樣本主要分為兩部分，訓練集和測試集，訓練集用于網絡的學習，測試集用于驗證網絡的預測精度。在對本研究建好的網絡進行訓練時，為了盡可能使樣本充分覆蓋全工況范圍，因此隨機取240組穩態試驗樣本作為訓練集，剩下60組作為測試集。

由于瞬態工況關注參數隨時間的變化規律，因此網絡輸入輸出均應為連續變化的曲線，如圖5所示。在對網絡進行訓練時，取一定的時間間隔，然后對樣本曲線進行取點，輸入輸出要一一對應，對于每一種工況，輸入的排列是有序的，這樣可以將模型的輸入看作是一條一條的曲線，得到的輸出也是曲線。在本研究中，取42組瞬態試驗樣本作為訓練集，測試集選擇起點為40%負荷、終點為100%負荷、兩階段增加的瞬態工況樣本，如圖6所示，第一段經過10 s提升到75%負荷，第二段經過15 s提升到100%負荷。

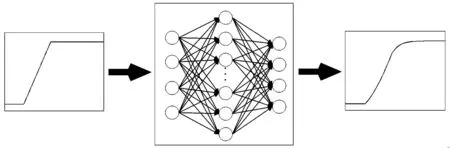
圖5 瞬態工況輸入和輸出形式

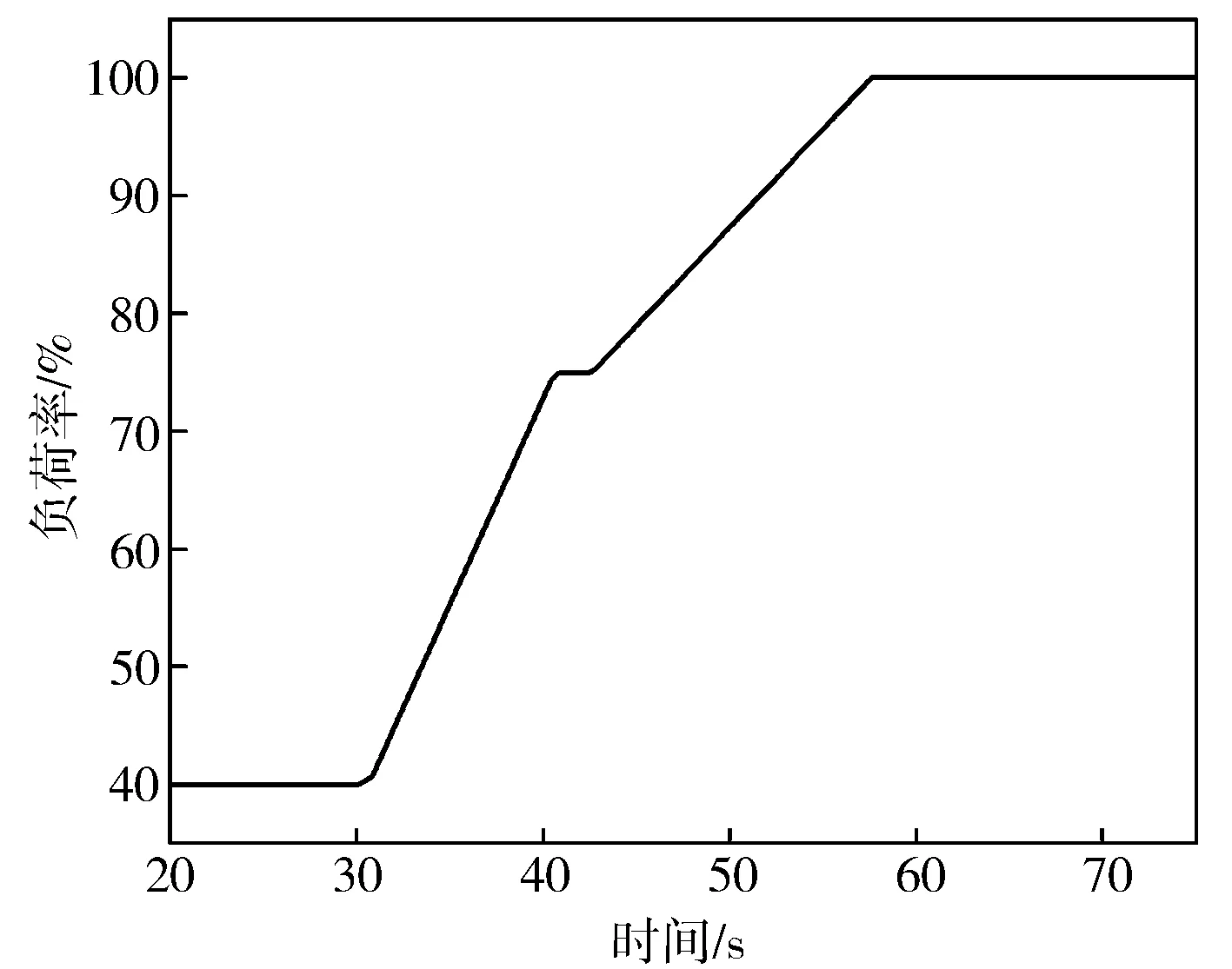
圖6 測試集負荷變動

1.4 普通BP網絡存在的問題

用上述結構的網絡先對訓練樣本進行學習，然后用測試樣本來驗證網絡的泛化效果。由于BP網絡初始權值具有隨機性，使得預測效果有所波動，因此取多次訓練的最優結果。瞬態和穩態的預測值和樣本值的誤差如圖7和圖8所示。在圖7中，增壓壓力瞬態訓練的最大誤差達到7.89%；在圖8中，缸內燃燒壓力穩態訓練的最大誤差達到7.62%。預測效果不佳可能是因為使用簡單的BP神經網絡會陷入局部最優，導致泛化效果比較差，無法滿足精度要求。因此，需要選擇合適的算法來對神經網絡進行優化。

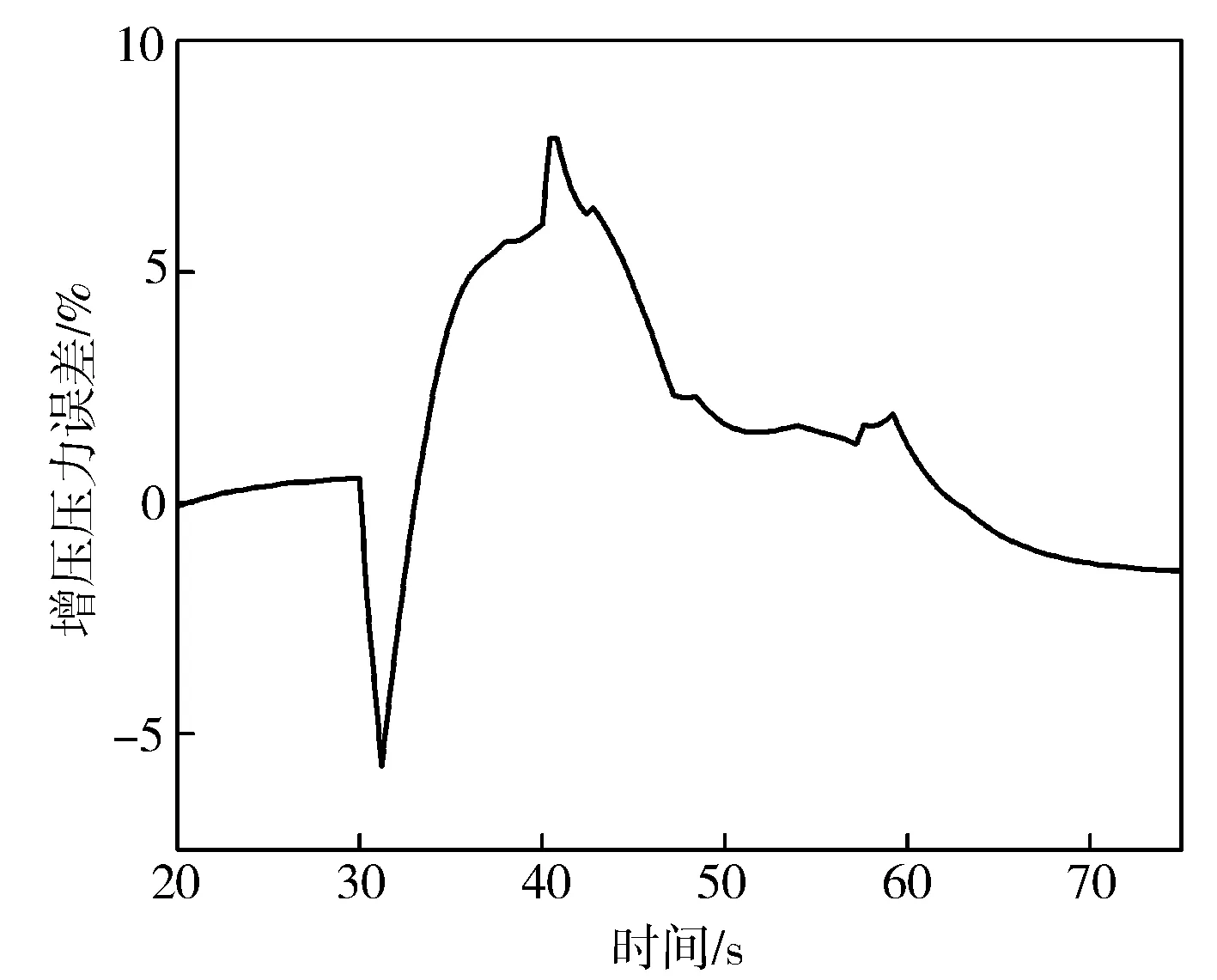
圖7 瞬態訓練結果對比

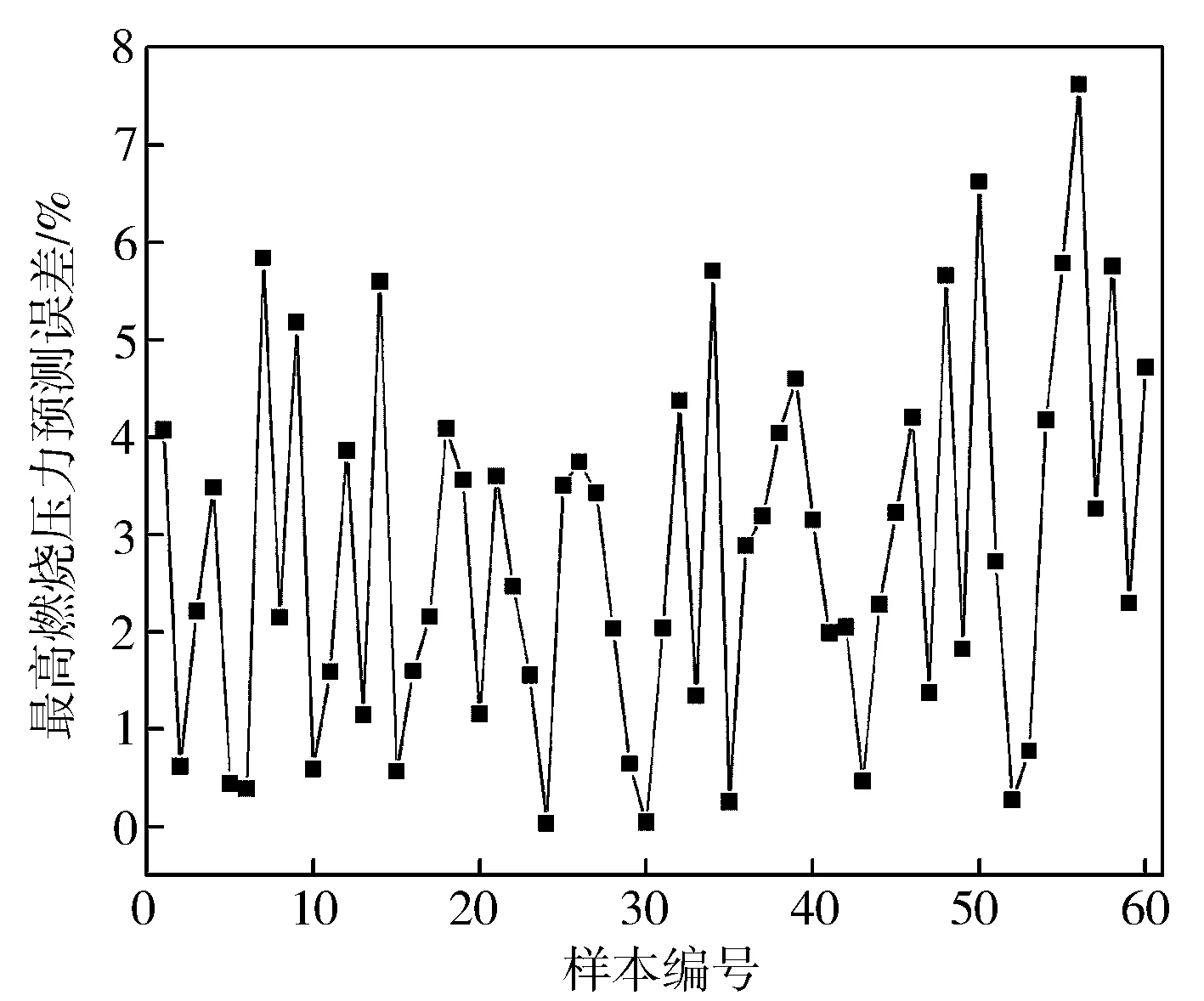
圖8 穩態訓練結果對比

2 粒子群算法

2.1 基本原理

粒子群算法是一種群智能優化算法，思想來源于對鳥類覓食行為的研究。鳥群在覓食過程中，初始狀態下每個個體的位置和方向是隨機的，但是在搜尋的過程中，通過個體之間信息的交互，大大提升搜尋的速度和效率[19]。基于此，粒子群算法的思想可以總結為粒子群體以一種隨機的初始狀態飛行，在每個時刻，每個粒子單獨搜尋的最優值稱為個體極值，個體極值中的最優值稱為全局最優值。通過總結迭代過程中群體的最優值來修正自身的飛行狀態，最終搜索到全局的最優解。

2.2 網絡優化過程

使用粒子群算法優化BP神經網絡(PSO-BP神經網絡)就要建立二者之間的關聯。優化的目的就在于尋找一組最優的網絡權值以及最佳的網絡結構，因此用粒子群中每個粒子的位置來表示當前的權值集合，粒子的維度與BP網絡的連接權值的數量相對應，通過反復的粒子搜索過程來確定最優權值。

粒子群算法優化BP神經網絡主要包括以下幾個步驟：

1) 構建粒子群，給各個粒子賦予隨機初始速度和位置。

2) 利用當前粒子群各個粒子的位置生成一組權值，構成網絡。在網絡的訓練空間中隨機抽取樣本作為訓練集，然后對網絡進行訓練。

3) 根據適應度函數計算各個粒子的適應度。適應度用來表征網絡的訓練誤差，然后根據適應度確定本次訓練的個體最優值和全局最優值。

4) 如果已經達到最大的訓練次數或者全局最優值滿足誤差界限，則將最優的權值賦予網絡，否則更新粒子的狀態然后繼續全局尋優，粒子狀態更新的表達式如下：

Vi(t+1)=ωVi(t)+C1r1(Pi(t)-Xi(t))+
C2r2(Pg(t)-Xi(t))，
Xi(t+1)=Xi(t)+Vi(t+1)，
r1=random(0,1)，
r2=random(0,1)。

式中：Vi為粒子的速度；Xi為粒子的位置；C1，C2為學習因子；ω為慣性權重；Pi為粒子個體極值；Pg為全局最優值。

優化算法的計算流程如圖9所示。

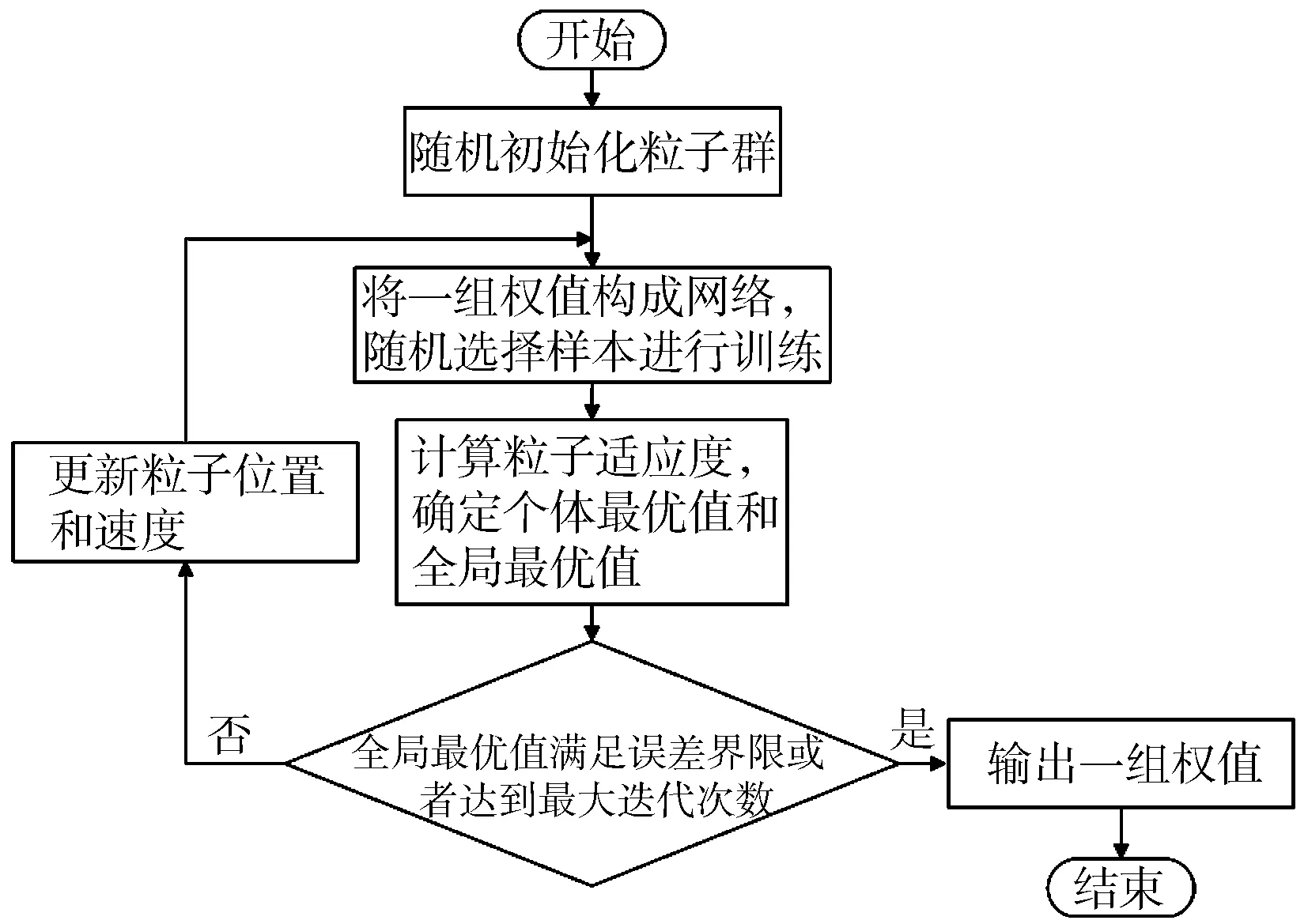
圖9 粒子群優化算法計算流程

2.3 PSO-BP神經網絡參數選擇

對于本研究所構建的PSO-BP神經網絡，網絡結構保持不變，輸入層節點個數為4，隱藏層節點個數為10，輸出層節點個數為4。隱藏層選擇Sigmoid函數，輸出層選擇線性函數，最大迭代次數為1 000。

對于粒子群的規模，即粒子群中粒子的個數，如果選取數值過大會導致學習效率降低，因此本研究中粒子群規模為50，粒子群算法的最大迭代次數選擇150，粒子的維數為94，學習因子C1，C2取1.5，慣性權重ω取1。

3 PSO-BP神經網絡與普通BP神經網絡對比

利用粒子群算法對本研究所構建的神經網絡模型進行優化，將穩態和瞬態訓練樣本輸入到網絡中進行學習，得到具有最優參數的網絡結構。用訓練好的網絡對穩態和瞬態測試樣本進行計算，驗證PSO-BP神經網絡是否能實現更好的預測效果。

本研究中選擇決定系數(R2)來表征預測值和試驗值之間的相關性[20]，從而體現模型的預測性能。決定系數的表達式如下：

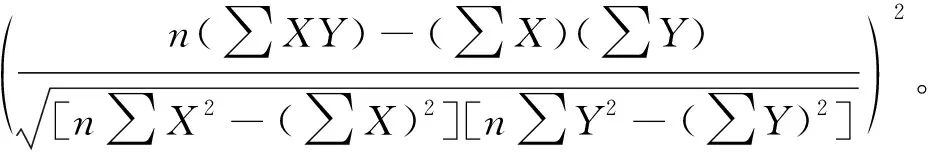
式中：X和Y分別對應預測值和訓練值。決定系數越大，表示預測值和試驗值之間的相關性越好，模型的預測性能越好。

用PSO-BP網絡對穩態測試樣本進行預測，分別計算增壓壓力、缸內最高燃燒壓力、渦前排溫、有效燃油消耗率的決定系數，得到普通BP神經網絡和PSO-BP神經網絡的預測效果對比，如圖10至圖13所示。

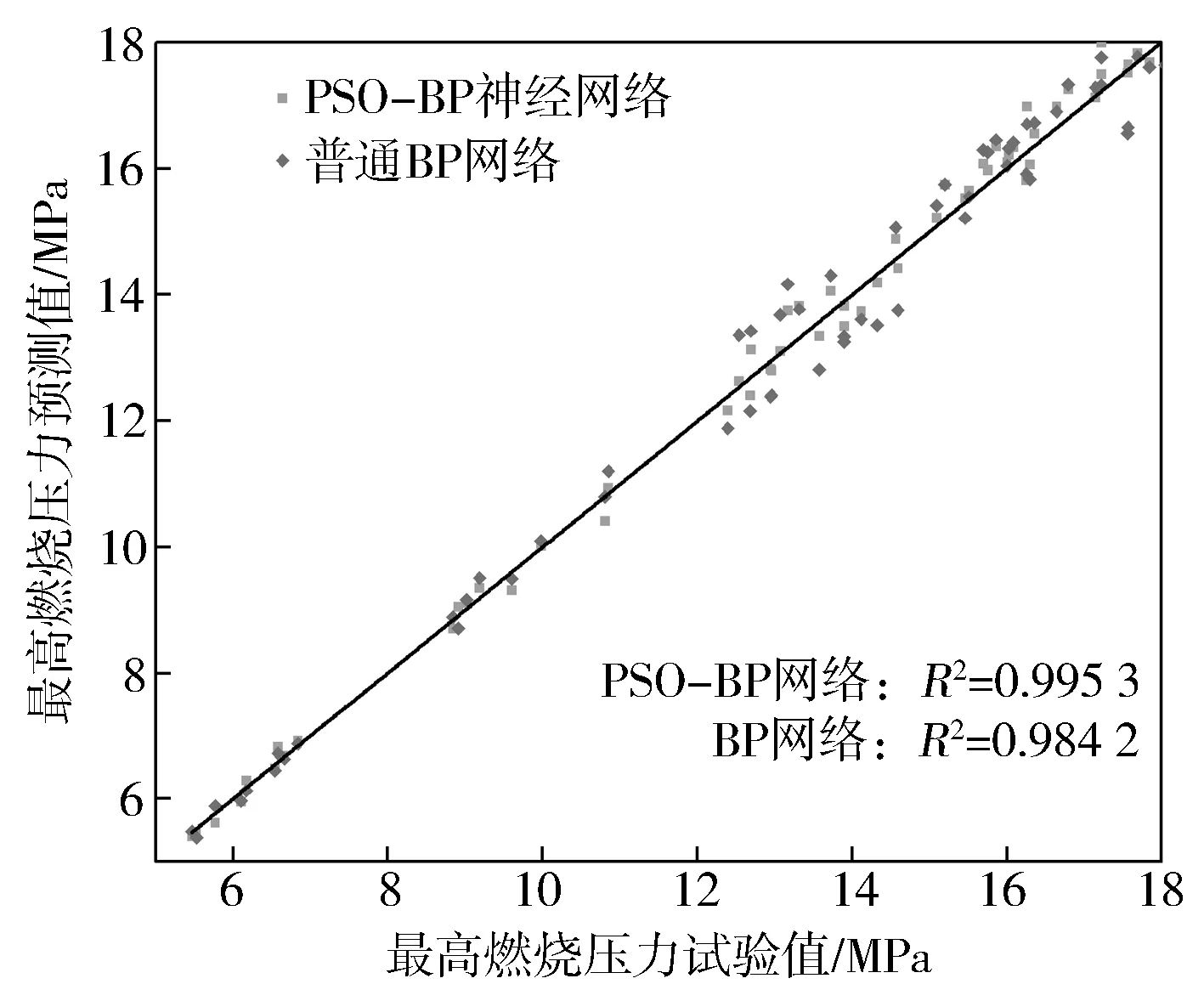
圖10 穩態最高燃燒壓力對比

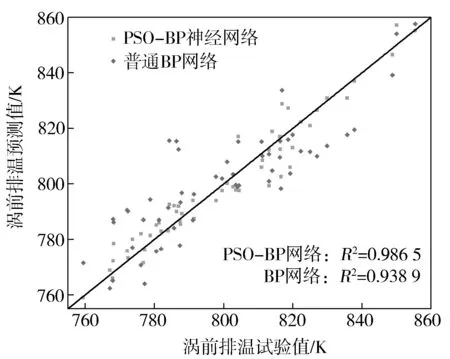
圖11 穩態渦前排溫對比

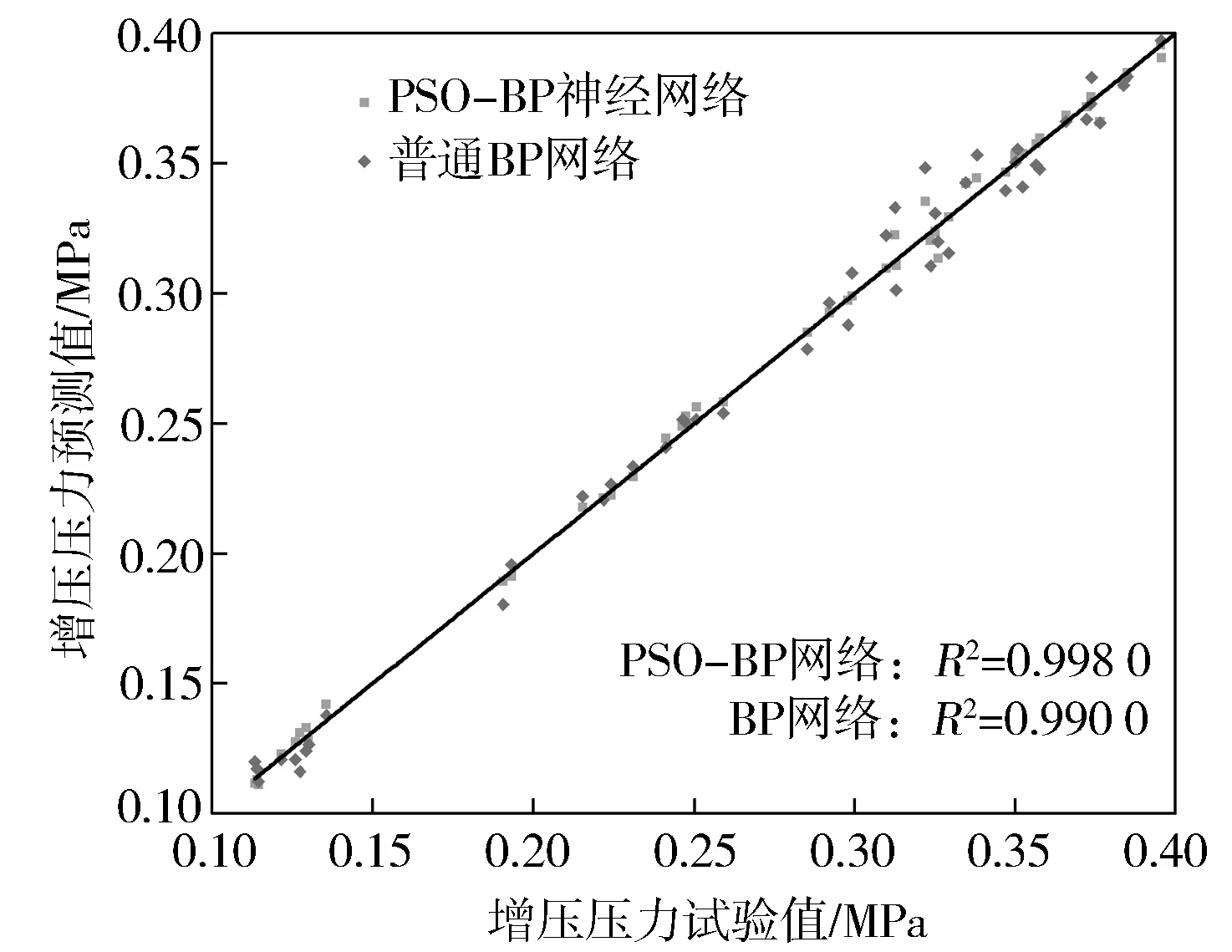
圖12 穩態增壓壓力對比

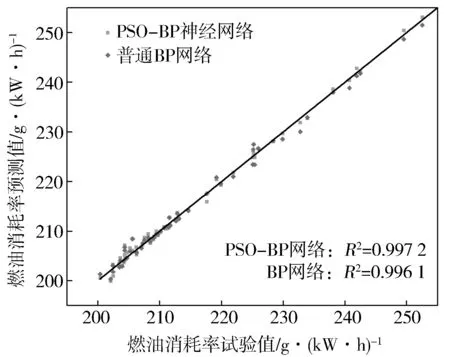
圖13 穩態燃油消耗率對比

對于穩態工況，PSO-BP神經網絡所有輸出變量的預測結果最大誤差為4.54%，而普通BP神經網絡所有輸出變量的預測結果最大誤差為8.78%。

對于瞬態工況的預測，輸出結果是參數隨時間變化的曲線，因此用每一時刻預測結果和訓練樣本的誤差曲線可以較為直觀地進行對比。瞬態工況下普通BP神經網絡和PSO-BP神經網絡的預測效果對比如圖14至圖17所示。

對于瞬態工況的預測，主要關注的是負荷變化階段的預測精度。從圖中可以看出，PSO-BP神經網絡和普通BP神經網絡在負荷穩定階段的預測精度基本相當，但是在負荷變化階段，普通BP神經網絡的預測誤差較大，尤其是在負荷變動的時間段，而PSO-BP神經網絡的預測精度有較為明顯的提升。

圖14 瞬態最高燃燒壓力對比

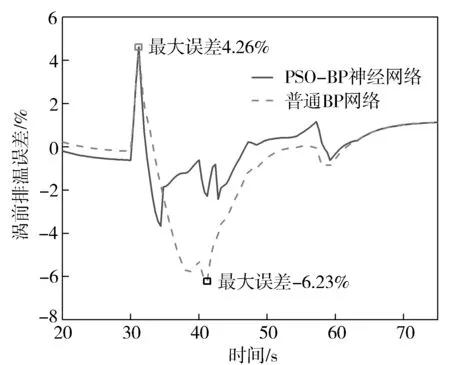
圖15 瞬態渦前排溫對比

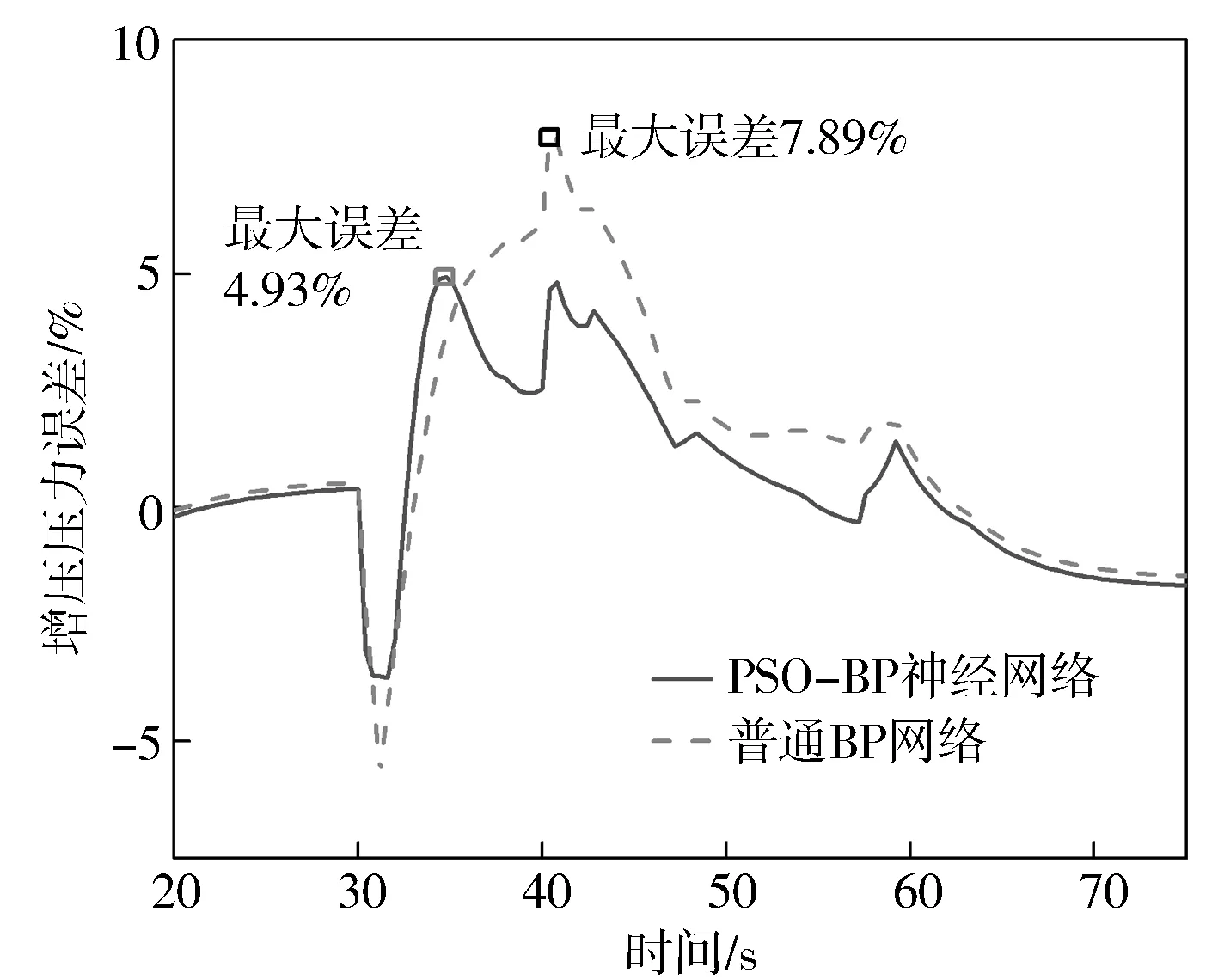
圖16 瞬態增壓壓力對比

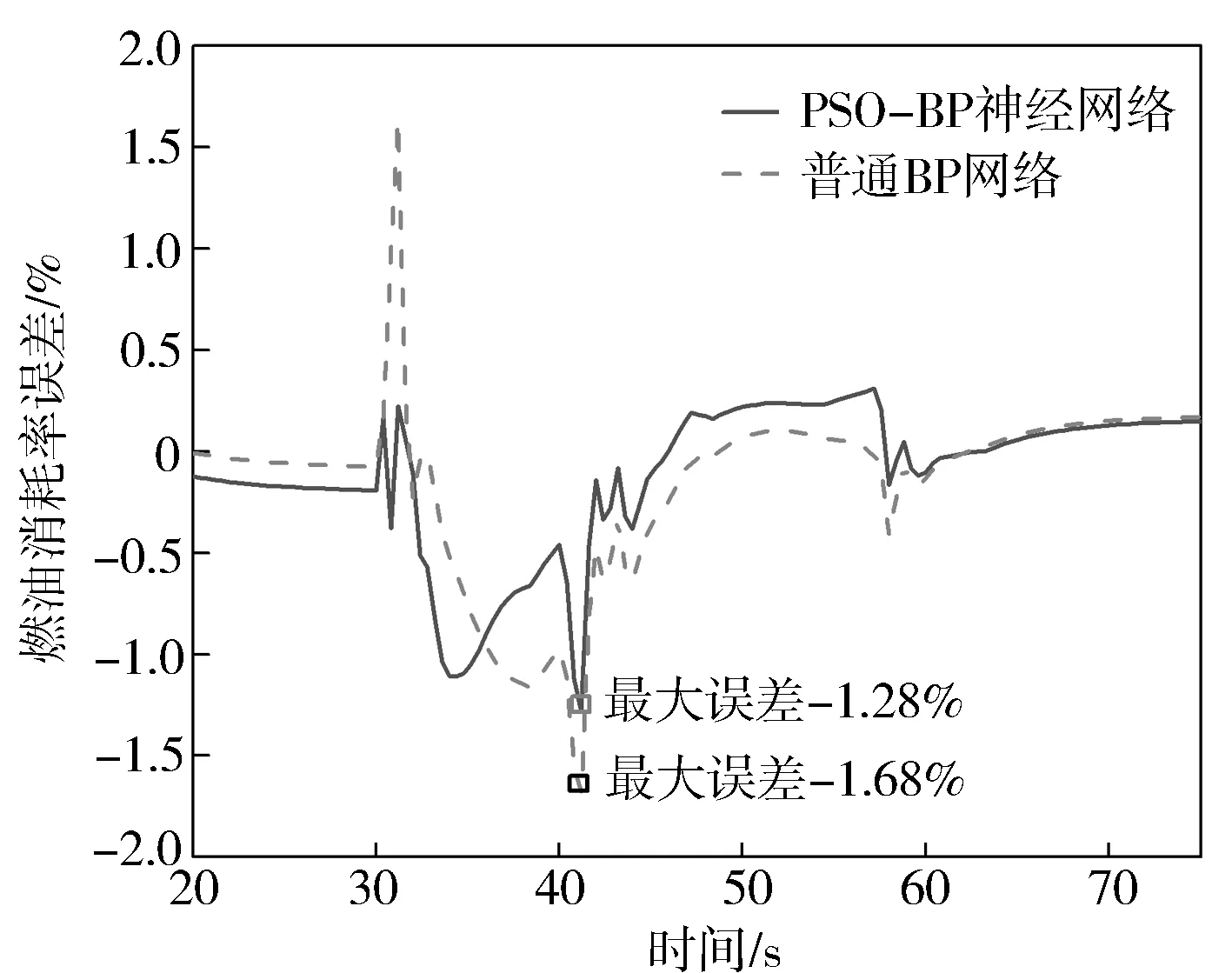
圖17 瞬態燃油消耗率對比

根據上面的分析可知，對于模型的輸出(最高燃燒壓力、渦前排溫、增壓壓力以及有效燃油消耗率)，在穩態工況和瞬態工況下，PSO-BP神經網絡模型均可以有效地進行預測，并且與試驗數據的相關性要明顯優于普通BP神經網絡，說明使用粒子群算法可以得到最優的權值和網絡結構，避免了局部陷阱。模型多次訓練的預測結果波動不明顯，說明PSO-BP網絡的預測穩定性更好，不需要進行多次訓練即可達到最優效果，訓練效率更好。

4 結束語

神經網絡是建立面向控制模型的一種有效的方法，可以應用在基于模型的控制系統標定工作中，后續可以將本研究的建模方法在實際控制系統的開發中應用。本研究所搭建的通用神經網絡結構不僅可以預測發動機的穩態性能，還可以有效預測發動機的瞬態性能，穩態工況最大誤差為4.54%，瞬態工況最大誤差為4.93%。普通BP神經網絡由于不能保證全局最優導致預測精度較差，利用粒子群算法對BP神經網絡進行優化，可以得到更優的網絡結構，模型的泛化能力可以得到提升，預測結果更加穩定，訓練效率更好；對于瞬態樣本的預測，PSO-BP神經網絡預測精度明顯優于普通BP網絡。