基于自適應高斯混合模型的軟件測試用例集約簡算法研究

楊永國

(中國人民解放軍91550部隊，遼寧 大連 116023)

0 引言

軟件規模越大，其邏輯復雜性越高，對這些軟件的可靠性要求也就越高。軟件的隱藏錯誤能夠造成其自身運行的失敗。也就是說軟件的隱藏錯誤是影響軟件可靠性的最關鍵因素之一[1]。對于小規模的軟件，工程實踐中大多采用人工設置斷點的方法來進行測試，以查找出錯誤。不過人工方法判斷錯誤位置較為復雜，且難度較大，不適用于大規模的軟件測試。因此，為了更加精準且高效地查找和消除軟件錯誤，專家學者們開展了廣泛的研究，提出了一些解決方法，并研發出對軟件進行單元、靜態和動態測試的工具軟件。這些方法和測試軟件，都要求測試用例集盡可能覆蓋全面，只有這樣才能精準地定位錯誤，提高測試的有效性[2-4]。但測試用例集包含的用例數量應該盡量約簡，以降低測試成本。

劉鋒等人提出基于向量相似度的測試用例集約簡方法[5]。張蕊等人提出一種基于搜索樹的用例約簡方法，求得約簡問題的全局最優解[6]。謝經緯在測試用例集約簡中引入需求分析，提出了兩階段用例集優化方法，分為需求切片和用例集優化兩個步驟[7]。張晨光等人提出一種在線測試用例集約簡方法，將測試集約簡嵌入測試生成流程內，測試生成過程為測試集約簡提供了測試序列與測試目標之間的滿足關系[8]。楊羊等人通過定義和合并基于ASM模型測試生成的等價遷移和等價狀態，減少了無效訪問狀態和無效遷移路徑的數量，實現了測試用例集空間的約簡[9]。蘇小紅等人采用面向錯誤定位需求的測試用例約簡方法，降低錯誤定位的復雜度，提高錯誤定位的精度[10]。

這些用來約簡測試用例集的方法還存在一些主要問題如下：1)如何建模測試用例集之間的關系，以提高查找軟件錯誤的準確度；2)如何實現參數設置的簡化，或者實現自適應的參數設置。為了解決這些問題，本文提出了一種基于自適應高斯混合模型的用例約簡算法。該算法引入高斯混合模型，尋找測試用例間的關系，抽取滿足測試需求的測試用例，實現用例集的約簡；同時通過自適應策略，簡化參數設置。

1 高斯混合模型

軟件測試用例集數據的概率分布通常很復雜，因此引入高斯混合模型來模擬逼近和約簡軟件測試用例集，以簡化問題[11-14]。高斯混合模型(GMM，gaussian mixture model)是M個高斯模型(聚類簇)的加權和，其對數據的M類概率密度分布進行高斯估計。每個高斯概率密度函數都與一個類對應。訓練時采用了期望最大(EM，expectation maximization)算法。

設每個樣本都對應于一個類，也就是對應于一個高斯概率密度函數，而整個樣本集對應M個高斯概率密度函數。但具體每個樣本xi對應于哪個高斯概率密度函數不確定，在GMM中，每個高斯概率密度函數所占的權重φj也不確定。式(1)所示為GMM:

(1)

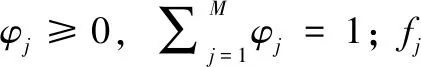
每一個高斯概率密度函數，也就是單高斯模型都有3個參數φj、μj、∑j。進行高斯混合模型建模時，就要確定3N個參數。

需要通過樣本集X={x1,xi,…,xN}來估計GMM的所有參數[15]Φ=(φ1,φj,…，φM)T，樣本xj的概率如式(2)所示:

(2)

其中:Cj為協方差矩陣。

對GMM參數進行估計，目前最多采用的是EM算法，其具體流程如下[15-19]：

2)后驗概率估計步驟。用式(3)估計φj的后驗概率:

(3)

3)最大化步驟。根據式(4)對權值φj進行更新:

(4)

根據式(5)對均值μj進行更新:

(5)

根據式(6)對方差矩陣Cj進行更新:

(6)

4)收斂條件。迭代計算步驟2)和步驟3)，權值φj、均值μj和方差矩陣Cj會不斷地更新，當p(X|Φ)-p(X|Φ)′<ε時停止進行迭代。p(X|Φ)′為更新權值φj、μj均值和方差矩陣Cj后根據式(3)計算的值，ε為閾值，一般ε=10-5。

2 基于自適應高斯混合模型

但采用的高斯混合模型聚類簇數目通常是經驗值，很容易造成聚類準確度的降低。具體到軟件測試用例集約簡的場景，經驗聚類簇數目對用例集多變的適應性較差，無法做到自適應。因此本文對高斯混合模型進行改進，使其可以自適應的確定聚類簇數目。

改進的思想為：使用K-means初始化EM，自適應地確定聚類簇數目，在此過程中能夠評判聚類結果，同時給出式高斯混合模型的所有參數，這些參數作為各個聚類簇進行新一輪迭代計算的參數，最終得到的結果更趨于最優解[15]。

針對軟件測試用例集約簡研究，為解決現有高斯混合模型聚類算法只能使用經驗聚類簇數目值的缺陷，根據上述改進思想，本文使用了自適應高斯混合模型算法，算法的具體實現步驟如下所述，實現流程如圖1所述。

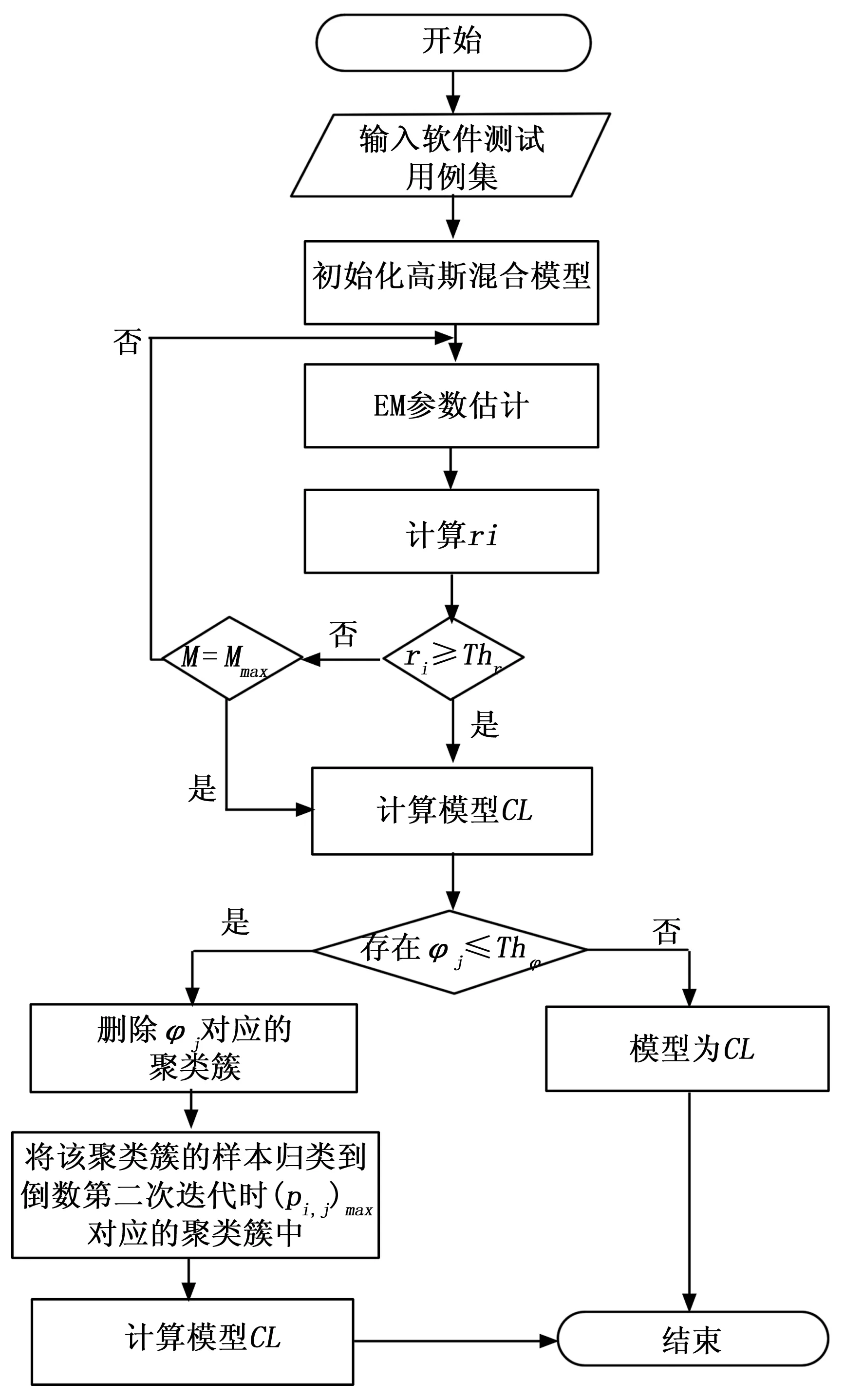
圖1 自適應高斯混合模型的實現流程

1)先按經驗設置M0個聚類簇，按照第1章節中的步驟(1)進行初始化協方差矩陣Cj、每個高斯概率密度函數所占的權重φj和均值μj，并用EM算法對模型進行優化，計算出初始化聚類結果。

2)在后續迭代計算的過程中，計算出第i個樣本xi屬于第j個聚類簇的概率pi,j。根據式(7)計算最大的(pi,j)max與排第二的(pi,jmax-1)的比值ri。第i個樣本xi聚類到某個聚類簇，要求(pi,j)max相對于(pi,j)max-1要有明顯的差別，即(pi,j)max應當比(pi,j)max-1大很多。也就是可以用ri來衡量聚類結果的優劣。ri越小，聚類結果越好；ri越大，聚類結果越差。

3)設定閾值Thr。通過給定Th的值，能夠衡量類聚類結果是否滿足要求。當ri≤Thr時，第i個樣本xi可以歸類為(pi,j)max對應的聚類簇；當ri>Thr時，第i個樣本xi不適合歸類為目前的所有聚類簇，需要增加聚類簇數目。聚類簇數目不能無限的增加下去，否則就失去了聚類的意義，需要設定一個最大聚類簇數目值Mmax。當聚類簇數目數目達到Mmax時，則第i個樣本可以歸類為(pi,j)max對應的聚類簇，而不再新增聚類簇的數目。

4)當聚類簇數目增加后，需要對新模型的參數進行初始化調整。迭代的重新執行步驟1)～3)，當聚類簇數目不再增加，或者達到最大時，完成模型訓練，得到模型參數。

5)當步驟4)得到的模型中，存在φj很小的聚類簇,即φj≤Thφ時，可將該聚類簇刪除，并將該聚類簇對應的樣本xj歸類到倒數第二次迭代時(pi,j)max對應的聚類簇中。因為聚類簇的φj≤Thφ時，可以認為該聚類簇的代表性不足。然后對模型進行計算，得到最終的模型CL，及模型參數。

3 實驗結果與分析

3.1 實驗數據集

本文采用使用廣泛并且便于比較的西門子軟件測試用例集[1,20]。該由Siemens Corporate Research的專家開發，含有7類程序代碼Print_tokens1、Print_tokens2、Schedule1、Schedule2、Replace、tacs和tot_info，每類程序代碼有1個無錯誤版本和一些含有錯誤的版本。軟件測試用例集中每類程序代碼的行數、初始測試用例數、程序中錯誤數、測試用例數如表1所示[1]。針對每類程序代碼，該軟件測試用例集使用了5種類型編程語言進行的代碼編寫，滿足常用編程語言需求的代碼需求。

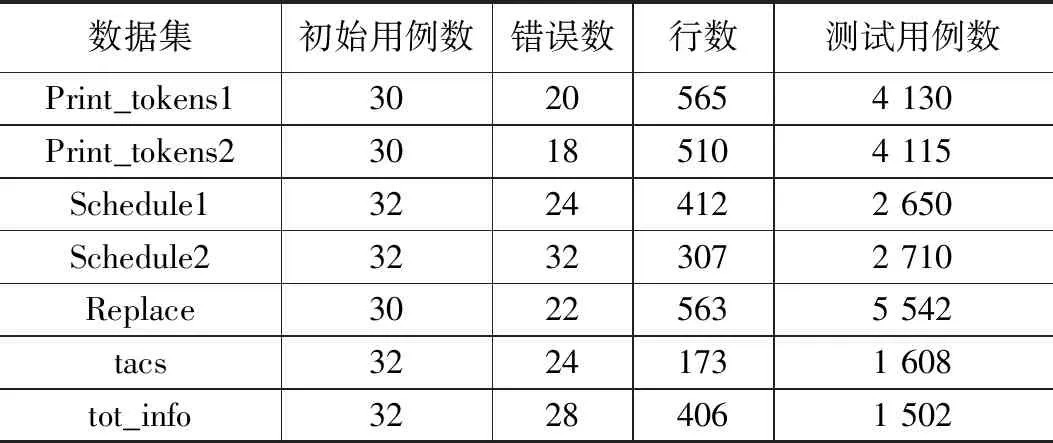
表1 軟件測試用例約簡用數據集

3.2 評價標準

實驗中，采用約簡率、錯誤檢測率和錯誤檢測丟失率這三個指標來評價實驗結果，以驗證算法的有效性、正確性和穩定性。

3.2.1 約簡率

約簡率計算如式(8)所示，為現有軟件測試用例集中的測試用例數目與約簡后軟件測試用例集中的測試用例數目的差值，比上現有軟件測試用例集中的測試用例數目，得到的比值[1]。

(8)

其中:RR為約簡率，|USN|表示現有軟件測試用例集中的測試用例數目；|USN′|表示約簡后軟件測試用例集中的測試用例數目。

3.2.2 錯誤檢測率

錯誤檢測率計算如式(9)所示，為約簡學習初始用例后，從測試用例中檢測到的程序代碼錯誤個數與測試用例中實際程序代碼錯誤個數的比值[1]。

(9)

其中：EDR為錯誤檢測率，EN表示現有軟件測試用例集的測試用例包含的程序代碼錯誤數；EN′表示使用約簡算法學習初始用例后，從軟件測試用例集的測試用例中檢測出的程序代碼錯誤數。

3.2.3 錯誤檢測丟失率

錯誤檢測丟失率計算如式(10)所示，為約簡學習初始用例后，從測試用例中檢測到的程序代碼錯誤個數與測試用例中實際程序代碼錯誤個數的差值，比上測試用例中實際程序代碼錯誤個數，得到的比值[1]。

(10)

其中:ELR為錯誤檢測丟失率。

由式(8)、式(9)和式(10)可以比較高斯混合模型、模糊K-Means聚類模型和本文提出算法的約簡率、錯誤檢測率和誤差檢測丟失率。

3.3 實驗結果分析

為了驗證本文提出的基于自適應高斯混合模型的軟件測試用例集簡約算法的性能，對比分析了本文提出算法、基于高斯混合模型的軟件測試用例集簡約算法和基于模糊K-Means聚類模型的軟件測試用例集簡約算法。

3.3.1 約簡率分析

使用3種算法約簡后，得到的軟件測試用例集中的測試用例數量如表2所示[1]。

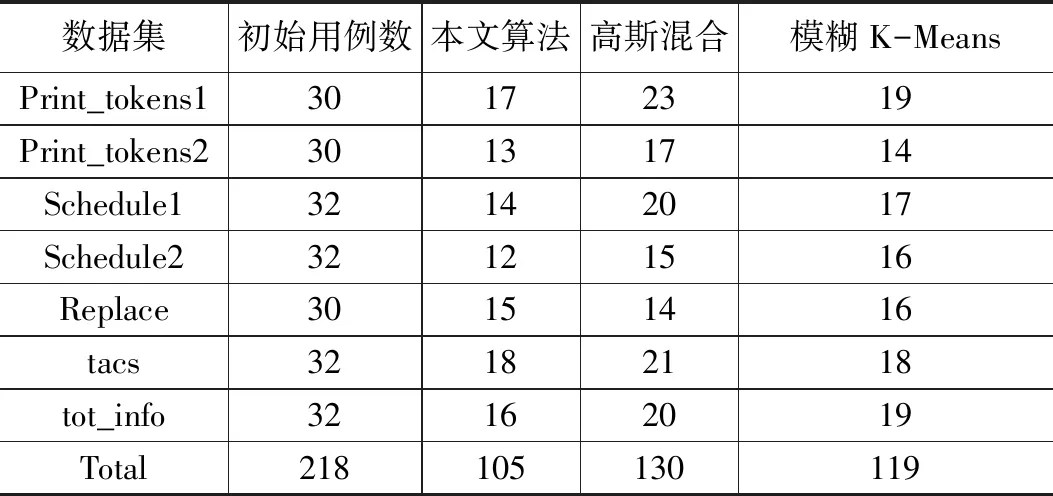
表2 約簡后的初始用例數

3種算法約簡率如表3所示[1]。通過分析，基于模糊K-Means聚類模型的軟件測試用例集簡約算法的約簡率優于基于高斯混合模型的軟件測試用例集簡約算法。本文提出算法的約簡率高于上述兩種算法，其總約簡率相對基于模糊K-Means聚類模型的軟件測試用例集簡約算法高11.46%，相對基于高斯混合模型的軟件測試用例集簡約算法高6.42%。約簡率的提升，可以在一定程度上降低軟件測試的復雜度，提高軟件測試的效率。

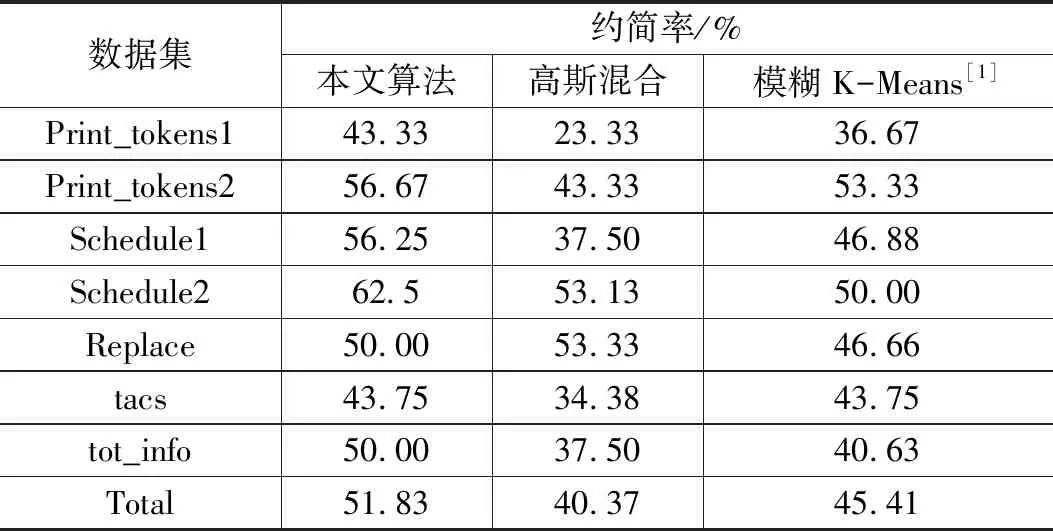
表3 3種算法的約簡率

3.3.2 錯誤檢測率分析

使用3種算法約簡后，從測試用例集中檢測出來的程序代碼錯誤數量如表4所示[1]。

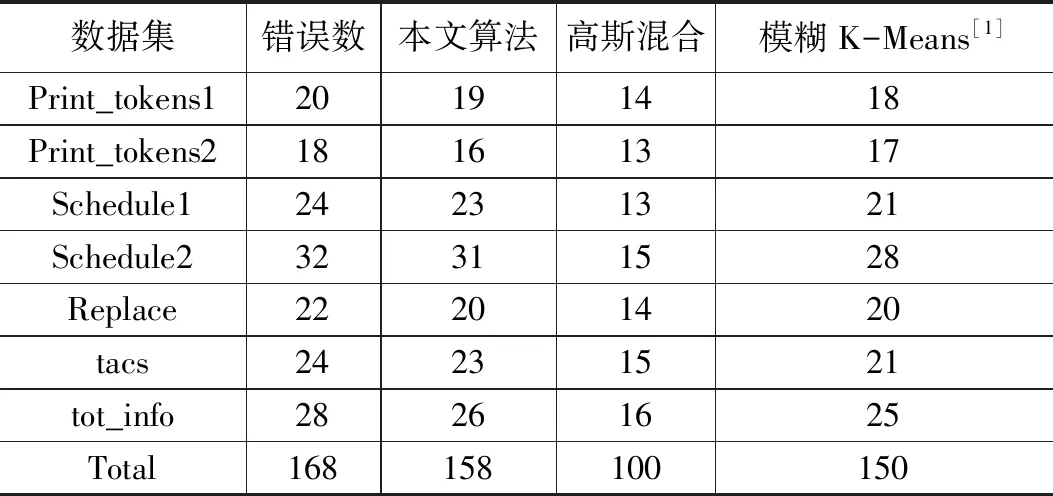
表4 約簡后的檢測出的錯誤數

3種算法的錯誤檢測率如表5所示。從表中數據可知，基于模糊K-Means聚類模型的軟件測試用例集簡約算法的錯誤檢測率優于基于高斯混合模型的軟件測試用例集簡約算法。本文提出算法的錯誤檢測率高于上述兩種算法，其總錯誤檢測率相對基于模糊K-Means聚類模型的軟件測試用例集簡約算法高34.53%，相對基于高斯混合模型的軟件測試用例集簡約算法高4.76%。使用本文提出算法能夠檢測出更多的錯誤數，可以提高軟件測試的可靠性，進而提高被測軟件的正確性。

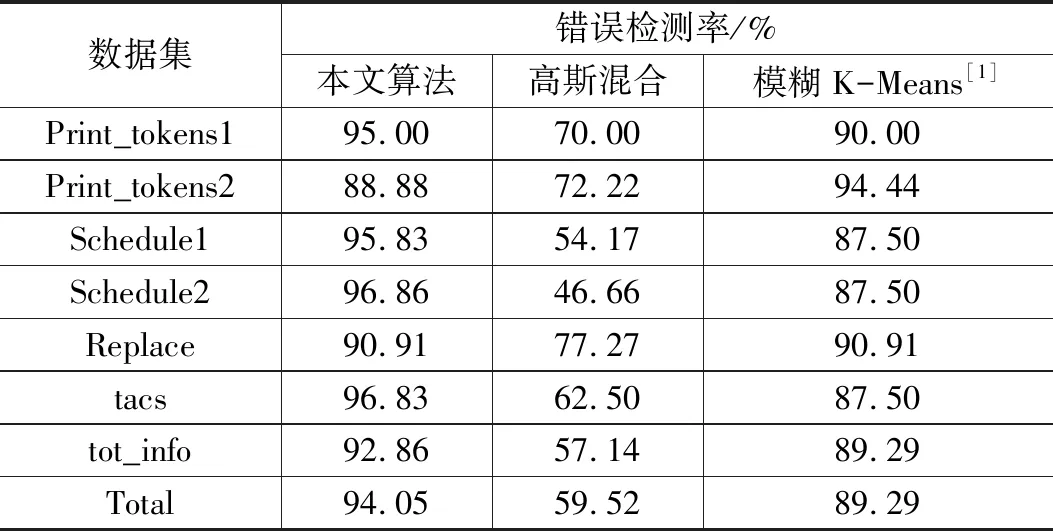
表5 3種算法的錯誤檢測率

3.3.3 錯誤檢測丟失率分析

3種算法的錯誤檢測丟失率如表6所示。

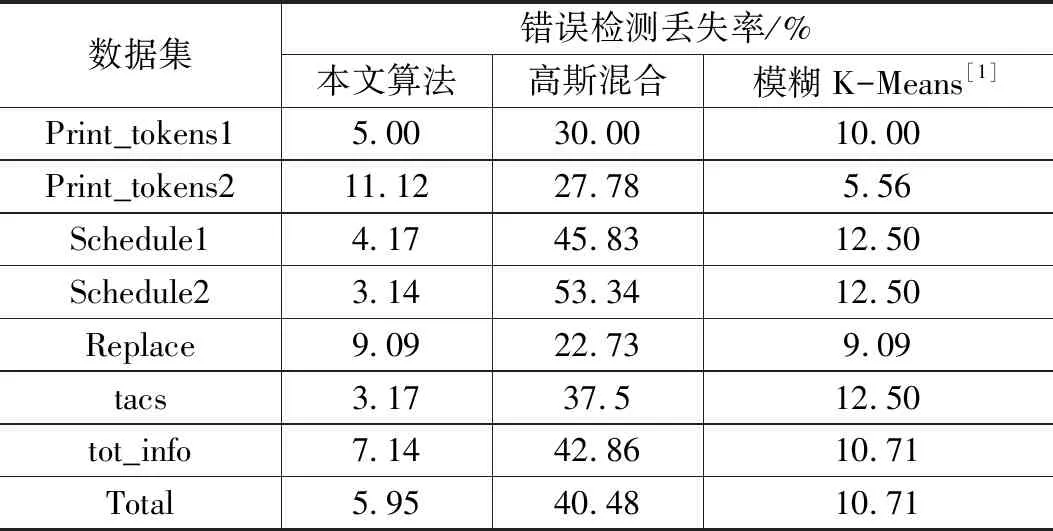
表6 3種算法的錯誤檢測丟失率

從表中數據可知，基于模糊K-Means聚類模型的軟件測試用例集簡約算法的錯誤檢測丟失率優于基于高斯混合模型的軟件測試用例集簡約算法。本文提出算法的錯誤檢測丟失率低于上述兩種算法。錯誤檢測丟失率低，代表漏檢的少錯誤數量，錯誤檢測丟失率越低越好。相對其它兩種算法，本文提出算法的錯誤檢測丟失率最低，這體現了提出算法約簡得到的測試用例集對程序代碼錯誤的覆蓋度較高。

4 結束語

軟件測試用例集聚類和約簡是一個時研時新且充滿挑戰的研究方向。當前軟件測試用例集聚類、約簡方法存在需要根據經驗給出聚類簇數目，導致自適應性不強的問題。本文提出了一種改進的高斯混合模型算法應用于軟件測試用例集約簡，以自適應的確定聚類簇的數目，并評估聚類效果的優劣。

提出的自適應高斯混合模型算法的優點是：算法在初始化和迭代過程中無需固定聚類簇數目，可以根據不同軟件測試用例集數據的特點自適應確定聚類簇數目，提升聚類的自適應性、準確性和泛化性，實現用例集最優約簡化。實驗結果表明，相對于高斯混合模型算法和模糊K-means聚類算法，提出算法的約簡率和錯誤檢測率更高。約簡后雖然軟件測試用例集規模精簡，但覆蓋率高。