糾正穩定和非穩定突發擦除錯誤的置換碼

何雅萍，賀玉成，2，周 林，2

(1.華僑大學 廈門市移動多媒體通信重點實驗室，福建 廈門 361021；2.西安電子科技大學 綜合業務網理論及關鍵技術國家重點實驗室，陜西 西安 710071)

閃存作為非易失性存儲方式的主流存儲器，具有低耗能、良好可靠性、高密度存儲等優勢，已被廣泛應用于便攜式電子設備、嵌入式設備等存儲部件。閃存數據通常受到電荷泄漏、單元間干擾、讀/寫干擾和數據保持噪聲等影響[1]，可能發生刪除、擦除、替換和移位等類型的錯誤，導致讀取數據與原始數據不一致[2-4]。近年來，面向閃存設備的糾錯編碼技術已成為差錯控制編碼領域的一個重要研究方向，其中基于置換理論的等級調制編碼技術可糾正閃存中的非對稱錯誤，是提高閃存設備可靠性的一個有效途徑[5-7]。

當某個閃存單元被破壞而無法讀出所存儲的電荷值時，在相應位置發生擦除或刪除錯誤。若錯誤位置已知，則發生擦除錯誤；若錯誤位置未知，則發生刪除錯誤。擦除或刪除錯誤進一步分為兩類：穩定錯誤和非穩定錯誤。在傳統的分組等級調制模型中，通常假設閃存單元組中各個單元可能發生的擦除錯誤或刪除錯誤相互獨立，不會影響到其他單元的等級描述，這類錯誤稱為“穩定錯誤”，要求不同等級對應的存儲電荷值之間具有足夠大的差值，同時要求各個單元的存儲電荷值保持高度穩定，從而具備足夠的抗干擾和抗噪聲的能力。隨著閃存容量不斷增大和封裝尺寸不斷減小的技術發展趨勢，為了降低實現成本，不同等級對應的存儲電荷值之間的差值越來越小；一個單元發生擦除錯誤或刪除錯誤，會影響到其他單元存儲電荷值的等級識別，這類錯誤稱為“非穩定錯誤”。進一步，由于閃存單元間寄生電容的耦合效應，使單元電荷向相鄰單元不斷滲透，從而導致連續多個閃存單元發生刪除或擦除錯誤，稱為突發刪除(Burst Deletion，BD)錯誤或突發擦除(Burst Erasure，BE)錯誤[8]，糾正非穩定的突發刪除或突發擦除錯誤更為困難。

近年來，LEVENSHTEIN首先提出一種可糾正單個刪除錯誤的置換碼[9]，奠定了置換碼的理論基礎。GABRYS等隨后提出了“穩定/非穩定”擦除(Stable/Unstable Erasure，SE/UE)、“穩定/非穩定”刪除(Stable/Unstable Deletion，SD/UD)等分類錯誤模型，并針對這些模型提出了相應的置換碼構造方法[10]。CHEE等先后提出了可糾正單個穩定和非穩定突發刪除錯誤的置換碼構造方法[8，11]。SALA等首先將多重置換碼應用于閃存差錯控制領域，提出糾正單個或多個非穩定刪除錯誤的多重置換碼構造方法[12]。HAN等提出可糾正穩定突發刪除錯誤的兩類置換碼和一類多重置換碼構造方法[13]，隨后MU與HAN等又提出兩類糾正單個非穩定的突發擦除錯誤的多重置換碼構造方法[14]。ZHAO等先后提出可糾正穩定和非穩定突發刪除錯誤的多重置換碼構造方法[15-16]。針對突發刪除錯誤的置換碼技術已逐步成熟，而針對突發擦除錯誤的置換碼還需進一步深入研究。

筆者主要研究等級調制下閃存單元的突發擦除錯誤，基于糾正單個刪除錯誤的LEVENSHTEIN置換碼[9]，提出一種置換碼的交織構造方法，可分別糾正穩定和非穩定的單突發擦除錯誤。給定交織深度為s，單突發長度≤2s的穩定擦除錯誤問題將分解為s個單突發長度≤ 2的穩定擦除錯誤問題，單突發長度≤s的非穩定擦除錯誤問題則分解為s個單非穩定擦除錯誤問題，分解后的子問題可直接采用LEVENSHTEIN置換碼的譯碼方法分別糾正。

1 基本概念

1.1 置換的基本概念

對于任意兩個整數m和n，若滿足m≤n，則可定義一個連續整數集合[m，n]={m，m+1，…，n}。當n為正整數時，可定義連續整數集[n]={1，2，…，n}，即[n]=[1，n]。集合[n]中所有元素的一個排列稱為一個置換，集合[n]上的所有置換構成置換群Sn，有|Sn|=n!。一般而言，任意有限集X上的所有置換可構成一個置換群，記為SX。若|X|=n，則SX和Sn同構。

定義1(逆置換) 令置換α=(α(1)，α(2)，…，α(n))∈Sn，其逆置換記為α-1=(α-1(1)，α-1(2)，…，α-1(n))∈Sn，若α(k)=i，則α-1(i)=k。

因此，α-1(i)表示元素i∈[n]在置換α中的位置值k，集合[n]表示置換α∈Sn中所有元素的位置集。

定義2(子置換) 令I?[n]表示一個位置子集，則置換α∈Sn中相應位置上的元素構成一個元素子集，記為α(I)={α(i)：i∈I}，這些元素保持原有次序可構成α的一個子置換，亦由α(I)表示。

定義3(等級映射) 設有限集X由n個任意不同的數值元素構成，每個元素x∈X按從小到大的次序，必在[n]中惟一對應一個元素k，記為φ(x)=k，則k稱為元素x的次序值或“相對等級”，φ稱為集合X到集合[n]的相對等級映射，對β=(β1，β2，…，βn)∈SX，令φ(β)=(φ(β1)，φ(β2)，…，φ(βn))，則φ(β)∈Sn稱為β的相對等級置換。

例1 設α=(5，3，6，1，4，2)∈S6，則α-1=(4，6，2，5，1，3)∈S6，α-1(1)=4表示α中元素“1”在第4個位置，α-1(2)=6表示α中元素“2”在第6個位置，以此類推。設I={1，4，5}，有α(I)={5，1，4}。

例2 設X={1，2，5，7，10，13}，|X|=6，則相對等級映射φ表示如下：

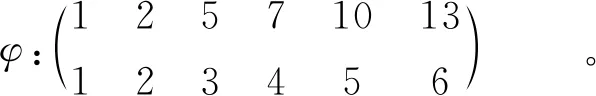
設β=(5，10，2，7，1，13)∈SX，則φ(β)=(3，5，2，4，1，6)∈S6。

1.2 等級調制下的擦除錯誤模型

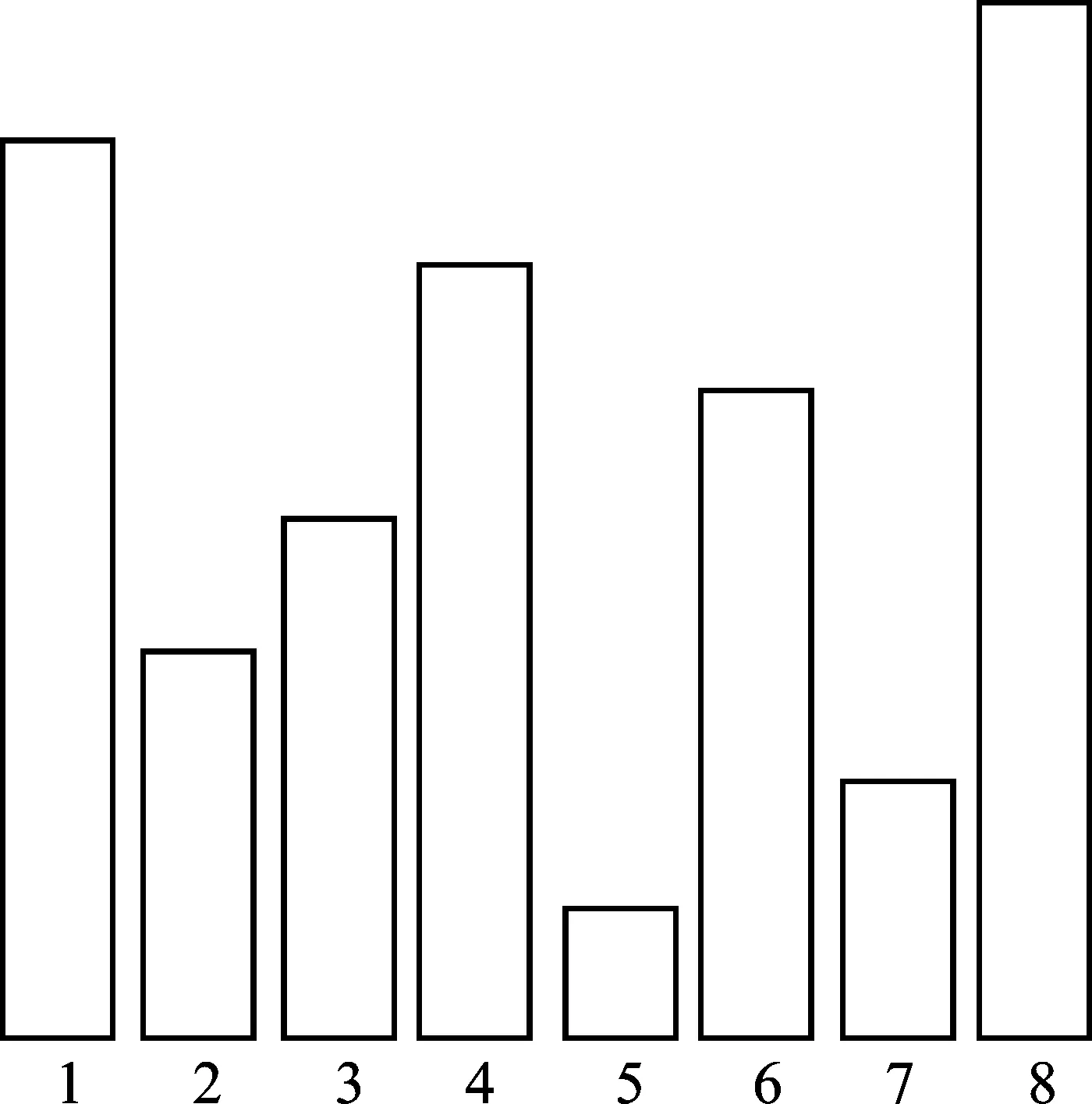
α=(7，3，4，6，1，5，2，8)圖1 閃存單元組等級調制的相對等級置換

采用等級調制方式的閃存設備對數據進行分組存儲，分組數據對應表示相同長度閃存單元組存儲電荷值的相對等級置換，即實數向量的相對等級置換。當采用置換碼時，閃存單元組中每個閃存單元的存儲電荷值不同[4]。當采用多重置換碼時，不同閃存單元的存儲電荷值可以相同[12]。圖1給出了分組長度為n=8的一個閃存單元組等級調制的置換表示，閃存單元的位置順序為1到8，閃存單元的存儲電荷值表示為直方圖，其中第5單元的電荷值最低，第8單元的電荷值最高，相對等級置換為α=(7，3，4，6，1，5，2，8)∈S8。

等級調制閃存的穩定擦除錯誤模型和非穩定擦除錯誤模型統一定義如下。

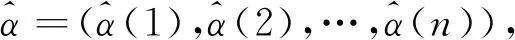
(1) 穩定擦除模型

(1)

(2) 非穩定擦除模型

(2)

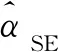
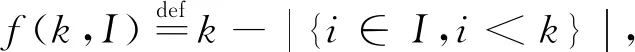
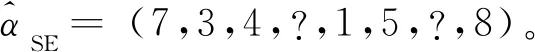
1.3 糾正單擦除錯誤的置換碼

LEVENSHTEIN碼是一類可糾正單個穩定刪除錯誤的置換碼，碼構造定義如下[9]。

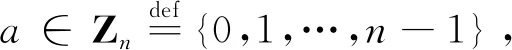
(3)

其中，當α(j)≤α(j+1)時，μ(α(j))=1；否則，μ(α(j))=0。則μ(α)=(μ(α(1))，μ(α(2))，…，μ(α(n)))，稱為置換α的簽名[9]。每個碼字的簽名是惟一的。

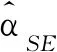
若碼字α在位置k∈[n]上發生單個非穩定擦除錯誤，則必存在i∈[n]，使得逆置換中α-1(i)=k，從而可確定被擦除的元素值為α(k)=i。因此，可利用LEVENSHTEIN碼字的逆置換來糾正單個非穩定擦除錯誤，具體定義如下。

定義6任意給定非負整數a∈Zn，可定義一個糾正單個非穩定擦除錯誤的置換碼為

(4)

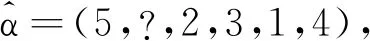
2 糾突發擦除錯誤的置換碼設計

針對等級調制下閃存的擦除錯誤，提出一種可糾正單個突發擦除錯誤的置換碼，給出了碼構造及相應的譯碼方法。

2.1 構造方法

定義7給定正整數s，令C?Sn為一個n長置換碼，如果碼C能糾正單個突發長度不超過s的穩定擦除錯誤，則稱為“≤s-SBE”置換碼。類似地，如果C能糾正單個突發長度不超過s的非穩定擦除錯誤，則稱為“≤s-UBE”置換碼。

給定s個置換碼Ci，i∈[s]，碼長遞減但相差不超過1，則根據定義8可構造一個交織碼為

C=C1°C2°…°Cs={β1°β2°…°βs：βi∈Ci，i∈[s]}。

(5)

應用上述的交織方法，結合定義5和定義6的糾錯碼構造方法，下面提出一種可糾正單個突發擦除錯誤的置換碼構造方法，可分別糾正單個突發長度≤2s的穩定擦除錯誤(≤2s-SBE)和單個突發長度≤s的非穩定擦除錯誤(≤s-UBE)。

構造：給定的正整數n，m，s，滿足n=sm，集合[n]劃分為s個互不相交的子集

Qi={j∈[n]：j≡i(mods)}，i∈[s]。

(6)

且|Qi|=m，令正整數ai，bi∈Zn，SQi為Qi上所有置換構成的置換群，結合定義5中糾正單個穩定刪除錯誤的置換碼和定義6中糾正單個非穩定擦除錯誤的置換碼

(7)

(8)

可構造一個置換碼

(9)

則碼CBE，n可分別糾正單個突發長度≤2s-SBE和單個突發長度≤s-UBE的兩種擦除錯誤。

2.2 譯碼方法

2.2.1 糾單個突發長度≤2 s的穩定擦除錯誤

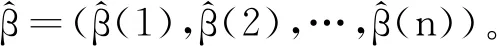
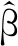
2.2.2 糾單個突發長度≤s的非穩定擦除錯誤

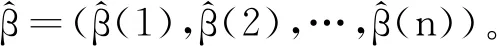
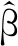
下面通過具體例子，來驗證單個≤2s-SBE錯誤和單個≤s-UBE錯誤的糾正。

例5 對于n=18，m=6，s=3，令CBE，n表示所得長度為n的置換碼。根據模s同余關系，將集合[n]劃分為3個子集：Q1={1，4，7，10，13，16}，Q2={2，5，8，11，14，17}，Q3={3，6，9，12，15，18}。任取3個置換β1∈Ca1

SD，6∩Cb1

UE，6，β2∈Ca2

SD，6，∩Cb2

UE，6，β3∈Ca3

SD，6∩Cb3

UE，6，經過交織生成一個碼字β1°β2°β3∈CBE，18。

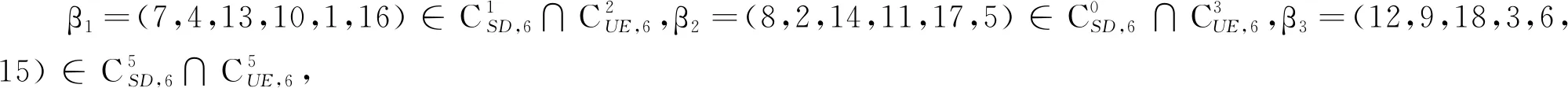
(1)假定發生5-SBE錯誤，錯誤位置集為I=[2，6]，讀取碼字為

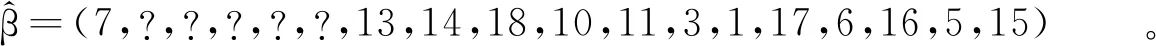
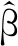
(2) 假定發生3-UBE錯誤，錯誤位置集為I=[5，7]，讀取碼字為

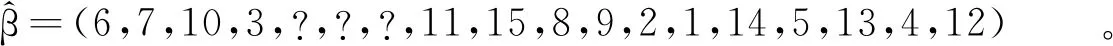
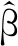
3 結束語

基于糾正單個刪除錯誤的LEVENSHTEIN置換碼構造方法，針對閃存單元等級調制下置換碼發生突發刪除錯誤的穩定性問題，結合置換交織技術，提出一種新的置換碼構造方法；可分別糾正單個突發長度≤2s的穩定擦除錯誤和單個突發長度≤s的非穩定擦除錯誤，并給出了相應的譯碼方法。最后通過實例驗證了所提出的構造和譯碼方法的有效性。