電容薄膜真空計用金屬膜片電容傳感器設計

侯少毅 胡強 衛紅 陳浩

開發設計

電容薄膜真空計用金屬膜片電容傳感器設計

侯少毅 胡強 衛紅 陳浩

（季華實驗室，廣東 佛山 528251）

金屬膜片電容傳感器是高精度電容薄膜真空計的關鍵部分。為滿足其國產化需求，以國內研發的某鎳基合金膜片材料為基礎，研究電容薄膜真空計用金屬膜片電容傳感器。首先，基于通用有限元分析軟件，建立金屬膜片電容傳感器中感應膜片的計算模型；然后，采用非線性大撓度理論對不同預應力下的感應膜片變形進行計算，并與理論計算結果進行對比，對比結果表明，該計算模型具有較高精度；最后，分析預應力與感應膜片非線性誤差關系，并對影響電容薄膜真空計測量特性的預應力、感應膜片與固定極板的初始極距等關鍵參數進行設計，以滿足高精度真空測量的要求。

電容薄膜真空計；感應膜片；預應力；初始極距

0 引言

電容薄膜真空計作為一種直接測量式、全壓型的真空計，具有靈敏度高、功耗低、穩定性好、精度高等特點[1]，且測量結果與氣體成分和種類無關，在真空行業應用廣泛，已成為半導體、航天、核工業等領域的重要儀表。由感應膜片、固定極板及電信號處理電路等組成的金屬膜片電容傳感器是電容薄膜真空計的核心部件。其中感應膜片的非線性誤差、感應膜片與固定極板的極距，直接關系到真空計測量的準確性和靈敏度等性能參數。

高精度電容薄膜真空計長期被國外壟斷，感應膜片關鍵材料主要依賴進口。為助其國產化，本文以國內研發的某鎳基合金膜片材料為基礎，根據金屬膜片電容傳感器感應膜片的厚度和直徑參數，采用通用有限元分析軟件對其變形及應力進行仿真計算，研究不同預應力下感應膜片的線性度誤差，設計感應膜片預應力；綜合分析該預應力下感應膜片的變形及應力強度，針對影響真空計測量特性的金屬膜片電容傳感器的感應膜片與固定極板的初始極距等關鍵參數進行優化設計，以滿足測量范圍為1.13 Pa ～1300 Pa的電容薄膜真空計需求。

1 電容薄膜真空計結構

電容薄膜真空計主要由接管、入口擋板、感應膜片（動電極）、腔體、固定極板以及電容信號處理電路等部分組成，如圖1所示。其中腔體被感應膜片分成2個密閉腔室，固定極板所在的腔室為參考腔室，通過吸氣泵長期維持在高真空狀態。固定極板與感應膜片組成一個可變的平行板式電容器。在測量真空度時，外部壓力作用在感應膜片上，引起感應膜片與固定極板的極距發生變化，進而引起電容值變化。因此，感應膜片由于壓力而產生的撓度被感知轉換成電容值變化，通過檢測電容值變化可獲得相應的壓力值。

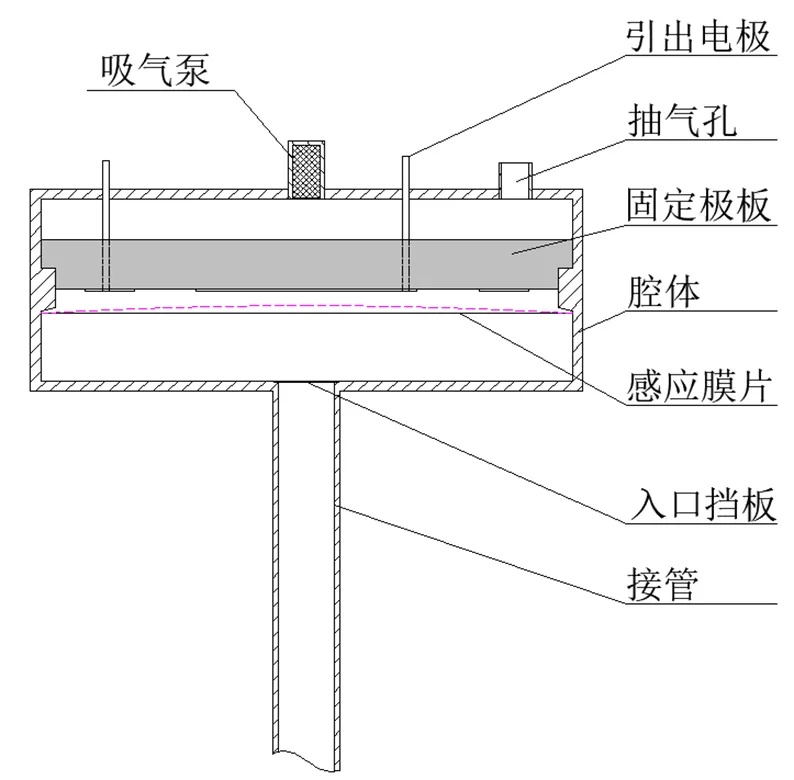
圖1 電容薄膜真空計結構示意圖

2 感應膜片有限元計算分析與設計

2.1 有限元建模與計算

以10Torr電容薄膜真空計（測量范圍1.13 Pa ～ 1300 Pa）為研究對象，選取感應膜片直徑為50 mm，厚度為0.025 mm，腔體和感應膜片的材料均采用國內研發的某鎳基合金材料，材料屬性如表1所示。

表1 國產某鎳基合金材料屬性

采用有限元分析軟件建立二維軸對稱模型，并利用該軟件的非線性計算能力，對感應膜片變形進行大撓度分析計算。為提高模擬精度，減少邊界效應的影響，建立包括感應膜片、腔體、接管等部件的完整模型。接管底部施加固定約束，感應膜片下側施加待測壓力，上側視為絕對真空，同時對感應膜片的預應力進行定義。由于整個腔體設計的剛度較大，分析時不考慮外部壓強的影響，并忽略腔體內壁小凸臺和抽氣孔、吸氣泵等結構的影響，以簡化模型。為提高計算精度，有限元模型采用四邊形軸對稱網格單元，并對其網格單元進行局部細化處理，在感應膜片厚度方向劃分為3層網格，有限元分析模型如圖2所示。

圖2 感應膜片有限元分析模型

感應膜片的預應力直接關系其變形特性，因此，需對預應力進行分析。本文對5種預應力（0 Mpa，10 Mpa，45 Mpa，100 Mpa和150 Mpa）感應膜片分別在1.33 Pa，100 Pa，300 Pa，500 Pa，700 Pa，900 Pa，1100 Pa和1300 Pa壓力作用下的應力及變形進行計算。為驗證模型的正確性，同時采用馮·卡門方程和Beams方程[2]分別對無預應力感應膜片和有預應力感應膜片的中心撓度進行計算，感應膜片中心位移如表2所示。

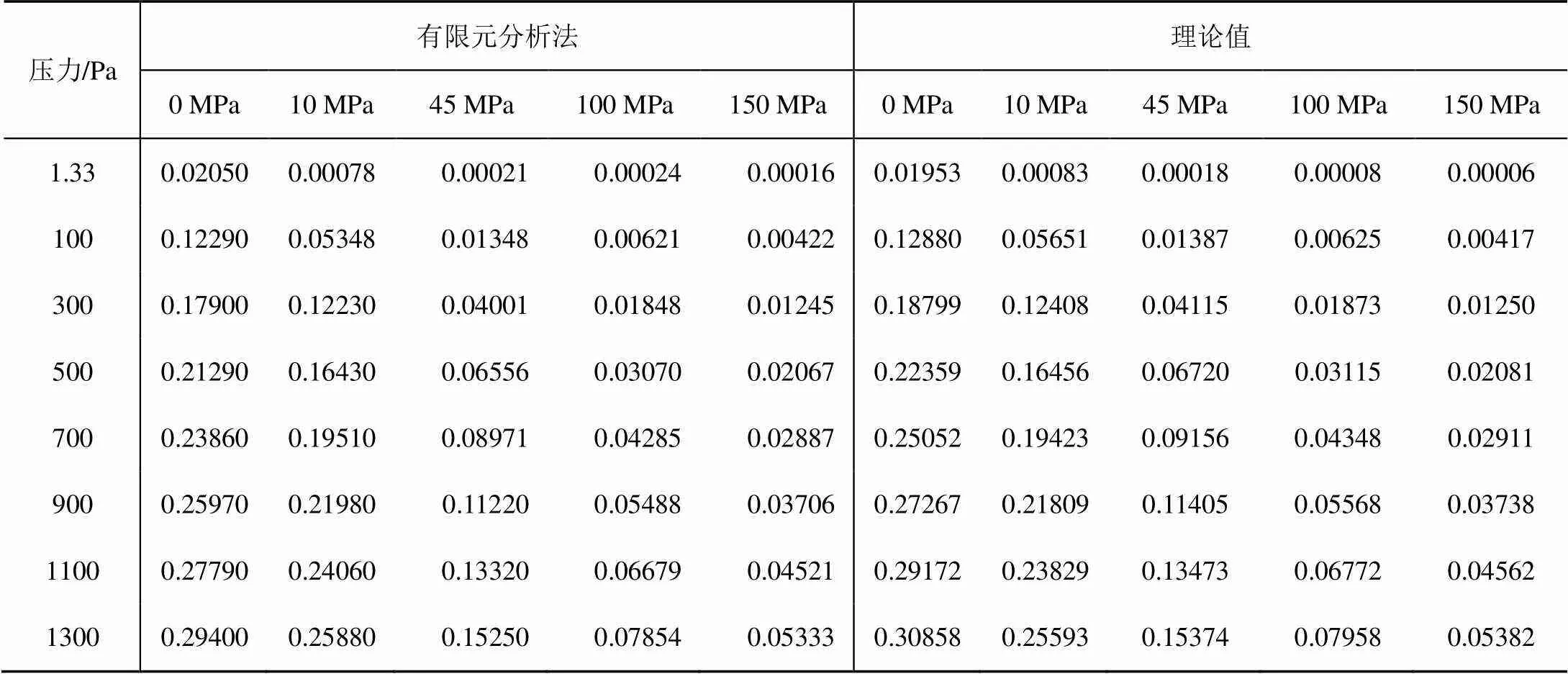
表2 不同預應力下感應膜片中心位移 （單位：mm）

由表2可見，有限元分析法計算結果與理論值接近，其最大偏差在6%以內（除受計算機精度、網格數量有限等帶來的誤差累積影響導致的小位移相對誤差較大外），表明有限元計算模型合理。

2.2 感應膜片變形線性分析

感應膜片壓力-撓度特性表現為近似線性[2]，減小非線性誤差對簡化數據處理、提高測量精度具有重要意義，因此，需對感應膜片的線性度進行分析。由表2的計算結果可得到感應膜片在不同預應力下的壓力-位移曲線，如圖3所示。由圖3可知，感應膜片的線性度隨預應力的增加而提高。

為對感應膜片變形的非線性度誤差進行定量分析，利用最小二乘法求出感應膜片在各預應力下壓力-位移的擬合直線，通過式(1)[3]可得到不同預應力下感應膜片變形的非線性誤差指標，結果如表3所示。

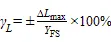
式中，為非線性誤差（線性度指標）；為最大非線性絕對誤差；為輸出滿量程。

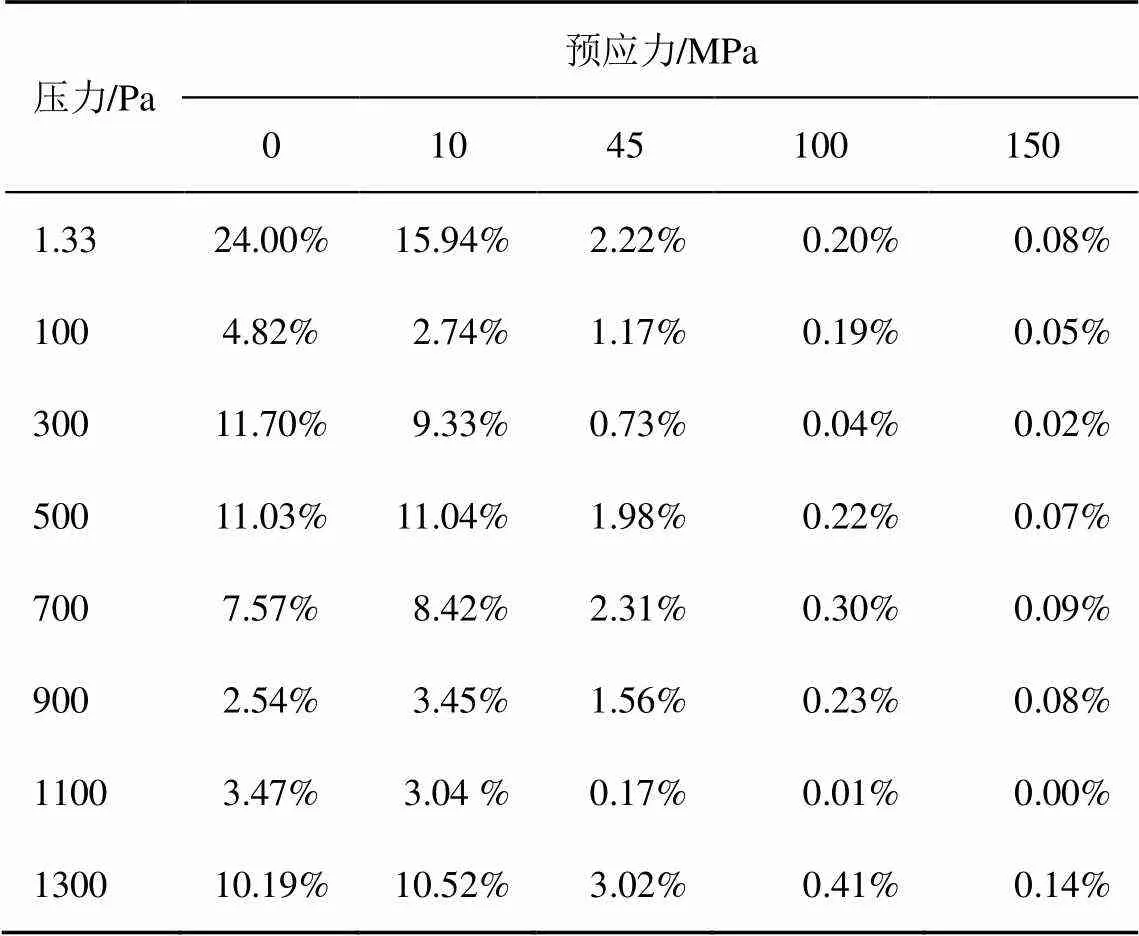
表3 感應膜片變形非線性誤差

由表3可知：在無預應力情況下，感應膜片中心位移在測量范圍內的非線性誤差達到24%，靈敏度為0.178 μm/Pa；當預應力為150 MPa時，測量范圍內非線性誤差減小到0.14%（優于文獻[4]膜片非線性度誤差0.3%的要求），靈敏度為0.041 μm/Pa（文獻[4]靈敏度0.0035 μm/Pa）。綜合考慮精度和靈敏度，本設計取感應膜片預應力為150 MPa。

3 感應膜片與固定極板初始極距設計

感應膜片與固定極板的初始極距需綜合考慮測量范圍、靈敏度、感應膜片強度等因素。根據無壓力時極距與電容值的關系：初始極距減小，基礎電容值增加，靈敏度提高[3]，但初始極距過小會減小測量范圍；初始極距過大將導致感應膜片承受過大的壓力，固定極板無法提供過載保護，導致感應膜片屈服失效。因此，為滿足電容傳感器測量范圍、靈敏度以及抗過載能力要求，需對感應膜片與固定極板的初始極距進行合理設計。

針對測量范圍為1.13 Pa～1300 Pa，感應膜片直徑為50 mm，厚度為0.025 mm，感應膜片預應力為150 MPa的電容薄膜真空計傳感器，采用前述有限元模型，分別對真空壓力大于量程的壓力載荷：1.3 kPa，4 kPa，8 kPa，12 kPa，16 kPa和20 kPa進行計算，其變形及應力分布分別如圖4、圖5所示。

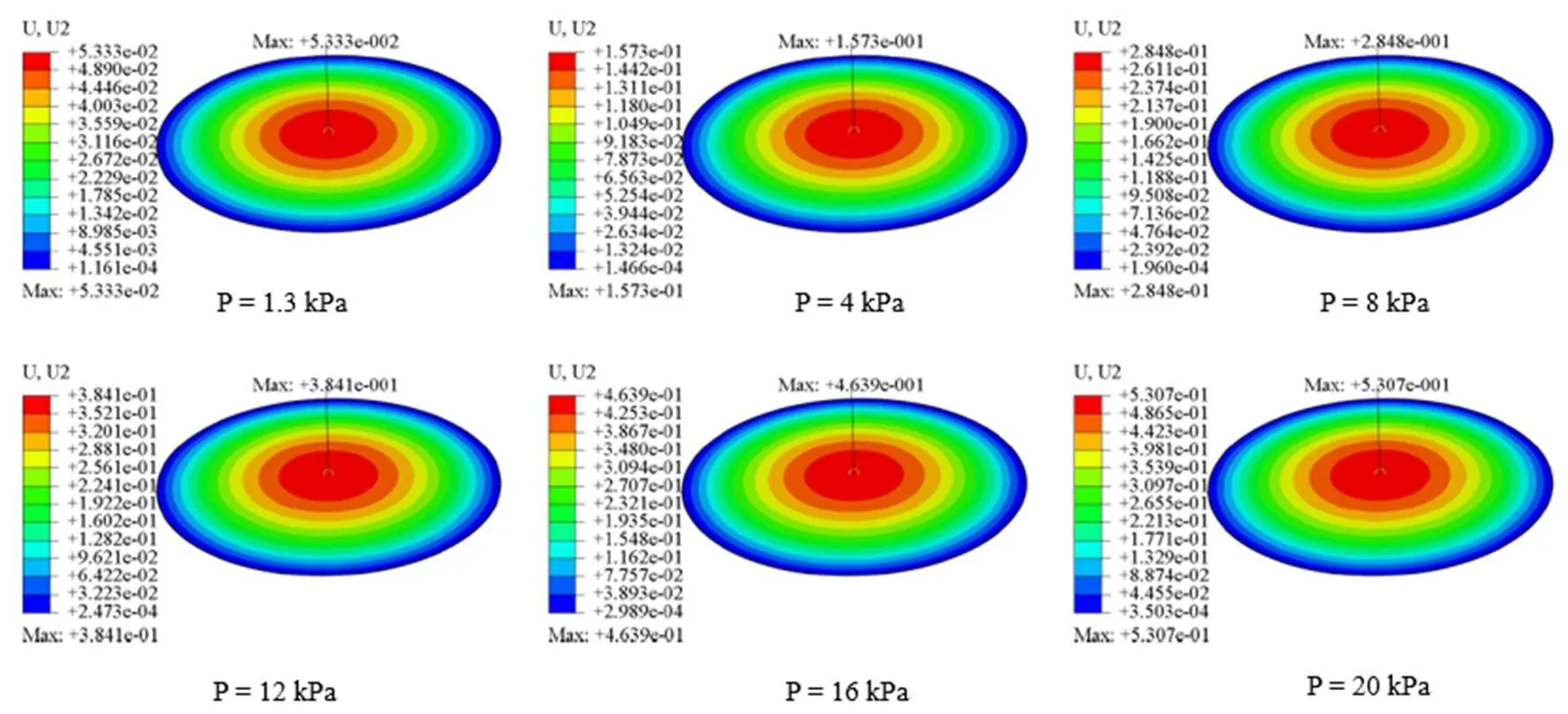
圖4 150 MPa預應力感應膜片在不同壓力下的變形

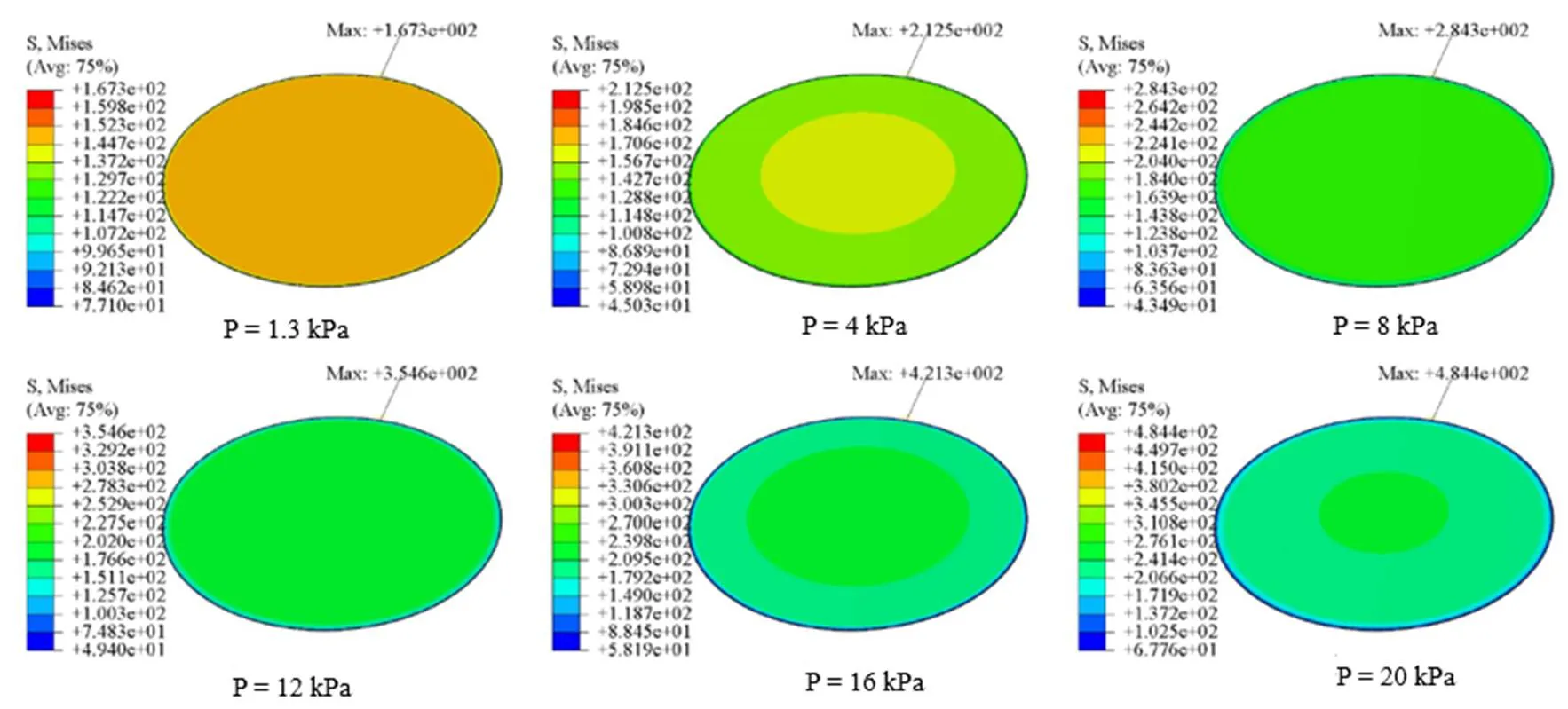
圖5 150 MPa預應力感應膜片在不同壓力下的Mises應力分布

由圖4和圖5可知：感應膜片在1.3 kPa壓力時，撓度為0.053 mm，感應膜片最大Mises為167.3 MPa，分布在邊緣，小于材料的許用強度350 MPa（安全系數取2），為滿足測量范圍要求，極距需大于0.06 mm；感應膜片在12 kPa壓力時，撓度為0.38 mm，感應膜片最大Mises為354.6 MPa，分布在邊緣，超過材料的許用強度350 MPa，為滿足感應膜片的抗過載能力，極距設計應小于0.38 mm。綜合考慮傳感器的測量范圍、靈敏度和抗過載能力要求，將感應膜片與固定極板的初始極距設計為0.1 mm。

4 結論

本文以國內研發的某鎳基合金材料為基礎，對測量范圍為1.13 Pa～1300 Pa，感應膜片直徑為50 mm，厚度為0.025 mm的電容薄膜真空計關鍵部件金屬膜片電容傳感器結構參數（預應力和初始極距）進行研究。

本文采用有限元通用分析軟件，對不同預應力下的感應膜片變形進行計算，研究預應力與感應膜片非線性誤差的關系。研究表明：隨著預應力的增加，感應膜片的非線性誤差逐漸減小，但過大的預應力會降低靈敏度。此外，分析感應膜片與固定極板的初始極距對測量范圍和過載能力的影響，初始極距過大會影響感應膜片的強度，過小則限制其測量范圍。最后，通過分析，確定感應膜片的預應力值為150 Mpa，初始極距為0.1 mm，可滿足電容薄膜真空計精度、靈敏度、抗過載能力等特性參數要求。

[1] Shahiri Tabarestania M, Azizollah Ganji B. Analytical Analysis of Capacitive Pressure Sensor with Clamped Diaphragm[J]. IJE TRANSACTIONS C: Aspects, 2013,26(3): 297-302.

[2] 孟岳,陳叔平,陳永軍,等.預加張力對電容薄膜真空計感壓膜片變形的影響[J].真空與低溫,2020,26(1):1-36.

[3] 胡向東,李銳,徐洋,等.傳感器技術與檢測技術[M].3版.北京: 機械工業出版社,2018.

[4] 張炳武.基于Havar合金膜片的電容式壓力傳感器研制[D].哈爾濱:哈爾濱工業大學,2016.

Design of Metal Diaphragm Capacitance Sensor for Capacitive Diaphragm Vacuum Gauge

Hou Shaoyi Hu Qiang Wei Hong Chen Hao

（Jihua Laboratory, Foshan 528251, China）

Metal diaphragm capacitance sensor is the key part of high precision capacitance diaphragm vacuum gauge. In order to meet the domestic demand, a metal diaphragm capacitive sensor for capacitive diaphragm vacuum gauge was studied based on a nickel based alloy diaphragm material developed in China. Firstly, based on the general finite element analysis software, the calculation model of the induction diaphragm in the metal diaphragm capacitance sensor is established; Then, the nonlinear large deflection theory is used to calculate the deformation of the induction diaphragm under different pre-stressing forces, and the comparison with the theoretical results shows that the calculation model has high accuracy; Finally, the nonlinear error relationship between pre-stress and induction diaphragm is analyzed, and the key parameters such as pre-stress, initial electrode distance between induction diaphragm and fixed plate which affect the measurement characteristics of capacitive diaphragm vacuum gauge are designed to meet the requirements of high-precision vacuum measurement.

capacitive diaphragm vacuum gauge; induction diaphragm; pre-stress; initial polar distance

侯少毅，男，1983年生，碩士研究生，工程師，主要研究方向：真空設備。E-mail: housy@jihualab.com

胡強，男，1979年生，博士研究生，研究員，主要研究方向：半導體裝備。E-mail: huqiang@jihualab.com

衛紅，男，1970年生，本科，高級工程師，主要研究方向：真空技術與設備。E-mail: weihong@jihualab.com

陳浩，男，1992年生，碩士研究生，工程師，主要研究方向：控制工程。E-mail: chenhao@jihualab.com

TB771

A

1674-2605(2021)03-0007-05

10.3969/j.issn.1674-2605.2021.03.007