Scratch三角函數與愛心畫法

前幾天在B站看到一個用Python結合函數繪制愛心的方法，我這樣一個充滿好奇心的人肯定也要試試看，而且還要把這種算法帶到Scratch中。

三角函數是基本初等函數之一，是以角度為自變量，角度對應任意終邊與單位圓交點坐標或其比值為因變量的函數。三角函數中常用的有正弦sin、余弦cos、正切tan三種。在Scratch中我們可以在運算模塊中調用這些函數（圖1）。

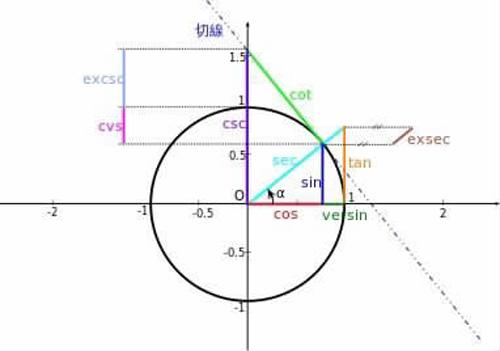
下面我們來繪制sin和cos函數，先將舞臺背景切換成坐標軸（Xy-grid），目的是為了清晰地了解繪制時的坐標情況。點擊擴展畫筆工具，將舞臺中的內容全部擦除，設置畫筆的粗細和顏色，并且添加一個變量“X的值”。很多同學會問，是不是需要再次添加一個變量“Y的值”呢？在只繪制三角函數時因為Y=sin（X）或Y=cos（X），Y直接用表達式寫出來就可以了（圖2）。

將畫筆移到最左邊，設X的值為-240，由于cos和sin在角度0-360之間的值是-1到1之間，為了讓曲線更明顯，我將sin（X）×100，擴大Y的變化值。同理將sin變為cos就可以繪制出cos曲線（圖3）。

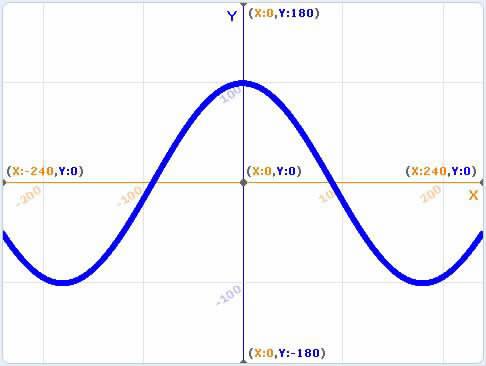
繪制完sin和cos三角函數曲線后我們可以開始繪制愛心圖形了。可以繪制出不同愛心的函數表達式有不少，最有名的笛卡爾曲線我們之前介紹過，搜索“matlab心形圖大全”，這里有多種平面和立體愛心的繪制公式。我挑選了一個較簡單不需要分段函數的愛心畫法（圖4）。

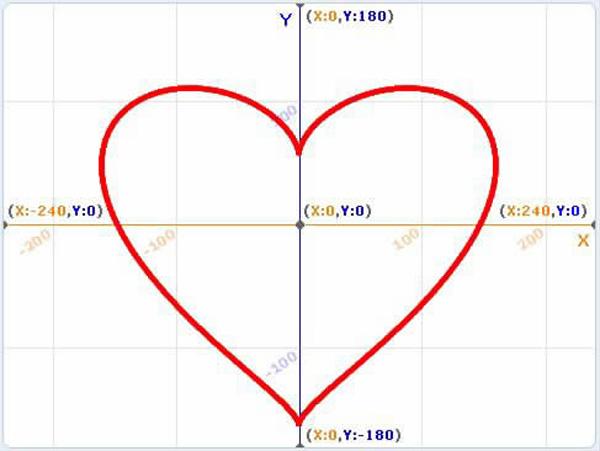
這個心形的坐標表達式如下：

X=16（sint）3

Y=13cos（t）-5cos（2t）-2cos（3t）-cos（4t）

根據公式我們需要三個變量T，X，Y。X的值和Y的值通過T的變化來控制，重復360次，每次將T的值增加1，X變量設置為16×（sint）3;Y變量設置為13×（cost）-5×cos（2×t）-2×cos（3×t）-cos（4×t），之后你就可以看到一個完美的愛心啦。之后可以展示給自己喜歡的人看（圖5）。

將公式轉化為代碼的難度并不大，大家還可以動一下腦筋，如何在此基礎上添加出一些不同的花樣呢？填充、漸變、特效……期待你的驚喜。