一種抗頻偏的定時同步方法及其性能分析 *

付博煒，李明齊

(1.中國科學院上海高等研究院，上海201210；2.上海科技大學 信息學院，上海 201210； 3.中國科學院大學，北京 100049)

0 引 言

在無線通信中，信號的同步至關重要。基于數據輔助的同步算法可以分為自相關定時同步算法和互相關定時同步算法兩大類[1]。

自相關定時同步算法的核心思想是在發送端發送特定的訓練序列(多段重復或共軛對稱的結構)，在接收端對接收數據做延時自相關運算。通過自相關結果對信號的起始位置和載波頻偏進行估計，實現簡單，在信噪比較高的情況下表現良好[2-3]。但由于自相關算法定時包絡不尖銳，而且相關的兩段輔助數據都會受到信道噪聲的干擾，自相關在低信噪比的情況下性能較差。

互相關定時同步算法的核心思想是在本地保存一份發送訓練序列，通過接收數據與本地序列做互相關運算。與自相關同步算法相比，互相關算法定時包絡尖銳，而且本地序列沒有受到噪聲和信道的影響，定時偏差小，適用于低信噪比的環境[4-7]。但互相關算法對載波頻偏敏感，隨著載波頻偏的增加性能會迅速下降。文獻[8]對互相關同步中載波頻偏的影響作了分析，通過限制訓練序列長度來減少載波頻偏的影響，但減少訓練序列長度同樣會降低定時同步的性能。文獻[9-10]通過粗頻偏估計的方法估計出載波頻偏，補償后進行細定時同步，該方法實現復雜度較高，需要額外的處理時延，而且同步性能受粗頻偏估計性能影響，只適用于短序列，信噪比較高的情況。文獻[11]提出了分段互相關的算法，將互相關運算分段進行以減少載波頻偏帶來的衰減，最后取絕對值相加得到同步判決度量。盡管該算法實現簡單并在實際系統中得到了應用，但分段絕對值的做法同時會放大噪聲的均值，增加接收機虛警的概率。

本文首先對載波頻偏的影響和傳統的分段互相關算法性能進行分析，在此基礎上提出了一種分段頻偏補償的算法，在傳統分段算法的基礎上，以頻偏補償代替絕對值操作。理論分析和仿真結果表明，在大頻偏的情況下，改進方法的同步性能要優于傳統分段算法。

1 互相關同步和載波頻偏影響

在加性高斯白噪聲(Additive White Gaussian Noise,AWGN)信道下，對于發送長度為N的訓練序列s(n),接收機接收到的信號為

r(n)=s(n)ej2πεn/N+w(n)。

(1)

定義ε=df/(fs/N)為歸一化載波頻偏，其中fs為采樣率，df為載波頻偏；w(n)為方差為σ2的加性高斯白噪聲。接收信號與本地序列的互相關結果為

(2)

得到歸一化定時同步判決度量為

(3)

不失一般性，假設發射信號和接收信號的功率為1。在同步時刻，同步判決度量為

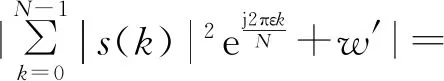
(4)

M(0)=|αN+w′|。

(5)

式中：α為頻偏衰減系數，

(6)

當ε<0.5時，通過二階泰勒展開可以近似為α=1-π2ε2/6，互相關峰值會隨著載波頻偏的增加而迅速變小，從而降低定時同步的性能。

接收信號的定時同步可以看作一個檢測判決問題：

(7)

式中：H1為正確同步假設，判決度量為互相關峰值與等效噪聲之和；H0為錯誤同步假設，判決度量為等效噪聲。當n=0時，M(n)服從萊斯分布，在互相關峰值αN遠大于噪聲功率σ2時，M(0)可以近似為均值為αN、方差為Nσ2/2的正態分布；當n≠0時，M(n)為方差為σ2復高斯噪聲的包絡，服從瑞利分布。

定義同步檢測概率為PD,虛警概率為PFA,根據奈曼-皮爾遜(Neyman-Pearson)引理，令判決門限為thr,則互相關同步算法的檢測概率為

(8)

虛警概率為

(9)

檢測概率和虛警概率的關系為

(10)

式中：Φ為標準正態分布的概率分布函數。從式(10)中可以看出，在虛警概率確定的情況下，互相關同步性能只與訓練序列長度、噪聲功率和載波頻偏有關，載波頻偏的增加會導致同步檢測概率的下降。

2 分段算法和性能分析

文獻[11]提出了一種分段算法，通過分段取絕對值的操作降低了載波頻偏的影響，將互相關運算分為L段，在n=0時，同步判決度量為

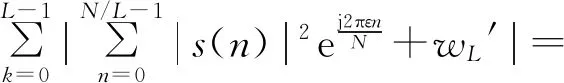
(11)

(12)

同步檢測概率可以近似為

(13)

3 改進的分段頻偏補償算法和性能分析

在互相關同步算法中，頻偏可以通過每段互相關的相位差求得：

(14)

式中：Pi(n)是每小段互相關的結果，

(15)

頻偏估計的結果可以近似為

(16)

頻偏估計誤差Δθ服從均值為0、方差為L2σ4/(4(L-1)3π2N2)的正態分布[12]。相比于定時同步，頻偏估計的結果受噪聲影響更小，結果更為準確。改進的頻偏補償算法的定時同步度量為

(17)

由于Δθ較小，若N>>σ2，在n=0時，Mpro(n)可以近似為均值為N(1-π2ε2/6L2)、方差為Nσ2/2的正態分布的隨機變量;當n≠0時，由于頻偏補償不改變同步結果的幅值，噪聲仍可以看作L段均值為0、方差為Nσ2/L的高斯噪聲wl的疊加：

(18)

式中：

(19)

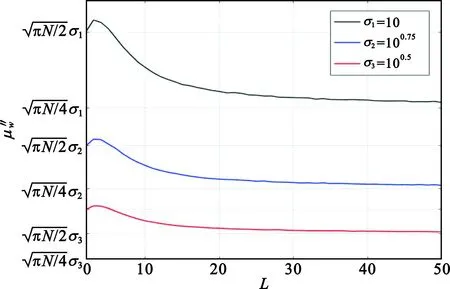
圖1 改進算法等效噪聲均值隨分段次數L的變化

圖2 改進算法等效噪聲方差隨分段次數L的變化

改進算法的虛警概率近似為

(21)

改進算法的同步檢測概率為

(22)

在低信噪比、大頻偏的場景中，改進算法的性能要優于傳統的分段算法。

4 實現復雜度分析

將長度為N、分段次數為L的傳統分段算法和改進分段算法的實現復雜度進行簡要分析，結果如表1所示。

表1 算法實現復雜度

在傳統分段算法中，頻偏估計在完成定時后進行，式(14)用于計算頻偏的三角函數模塊可以復用。而改進分段算法需要即時地計算出頻偏，并且對相關峰進行頻偏補償，頻偏估計中的三角函數模塊不能復用。但在序列長度N較大、分段次數L較小的情況下，改進分段算法增加的運算只占系統總運算量中很小的一部分，改進分段算法與傳統分段算法的實現復雜度相近。

相比于文獻[10]中的頻偏補償算法，改進算法不需要進行粗同步，頻偏估計結果可以在計算出互相關后即時得到，頻偏補償只需要對少量相關峰進行，無需額外的迭代運算，計算復雜度低，內存占用少，適合在實際工程中實現。

5 性能仿真與分析

為驗證理論分析結果，將分段互相關同步和本文提出的改進算法的定時同步性能進行仿真和對比。測試采用正交頻分復用(Orthogonal Frequency Division Multiplexing,OFDM)系統，載波頻率為fc=600 MHz,子載波間隔為3.75 kHz，同步訓練序列長度為N=4 096，以虛警概率PFA=10-3確定同步判決門限。在實際實現中，算法的實現復雜度會隨著分段次數L的增加而增加，當L=N時，算法的實現復雜度與文獻[10]中的頻偏補償算法相當。改進算法的分段次數不宜過大，在實現中可以根據接收信號的最大頻偏選擇合適的分段次數。

首先對理論分析結果進行驗證。圖3給出了改進算法式(22)中理論分析與實際仿真在不同頻偏下的AWGN信道下的定時同步性能。由于頻偏估計誤差和近似誤差的存在，算法實際性能略低于理論分析性能。從L=2到L=8，由于等效噪聲的方差有所增加，導致改進分段算法的同步檢測概率隨著分段次數L的增加而下降，但下降幅度較小。改進算法在分段次數較多的情況下仍然能夠保持較好的同步檢測性能。

圖3 AWGN信道下改進算法理論性能和實際性能的比較

圖4為相同虛警概率的情況下傳統分段算法和改進算法的定時同步性能。從仿真結果可以看出，一方面在沒有頻偏的情況下，不進行分段的互相關算法同步性能最好。無論是絕對值算法還是改進算法的同步性能都會隨著分段次數L的增加而有所下降。但相比于分段絕對值算法，改進算法由于分段造成的性能損失較小，在相同分段次數的情況下，改進算法的同步性能要優于絕對值算法。另一方面，隨著分段次數L的增加，系統的抗頻偏能力會得到增強，在大頻偏的情況下，分段帶來的抗頻偏增益要大于分段帶來的性能損失。改進算法可以通過增加更多的分段來獲得更強的抗頻偏能力。

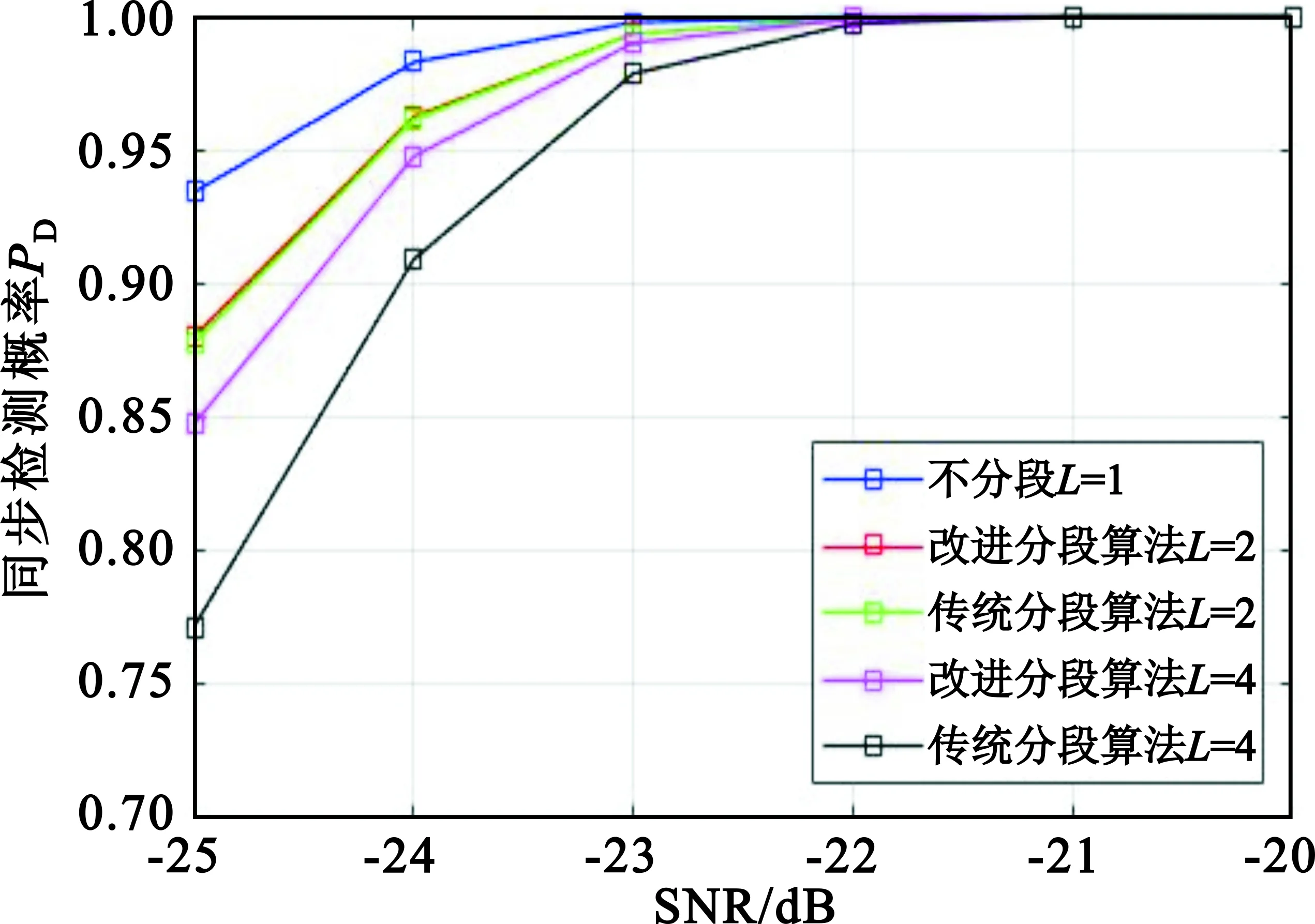
(a)歸一化頻偏ε=0

(b)歸一化頻偏ε=0.5圖4 AWGN信道下改進分段算法和傳統分段算法同步性能的比較

在多徑信道下，同步檢測算法主要是對最強徑(往往是第一徑)進行同步檢測和估計，AWGN信道下分析的改進算法可以推廣到多徑信道中。圖5為兩徑萊斯信道下改進算法和分段算法的仿真結果,信道第一徑和第二徑的增益分別為0 dB、-3 dB，萊斯因子為10，第二徑時延為2 μs。從仿真結果中可以看出，在多徑信道下，相同分段次數的改進算法的性能仍優于傳統的分段算法。

(a)歸一化頻偏ε=0

(b)歸一化頻偏ε=0.5圖5 多徑信道下改進分段算法和傳統分段算法同步性能的比較

6 結 論

本文對頻偏對互相關同步性能的影響以及傳統分段互相關同步的性能進行了分析。針對傳統分段互相關算法同步算法在低信噪比的情況下性能隨著分段次數增加而迅速下降的問題，提出了一種改進的分段頻偏補償互相關同步算法。理論分析和數值仿真表明，本文所提算法的同步性能要優于傳統分段互相關算法，適用于低信噪比、高頻偏的通信系統，具有很好的實用價值。