波輪式洗衣機懸掛結構力學特性研究

孫 震， 陳海衛*， 牟秋啟， 熊 明， 史亞成

(1.江南大學 機械工程學院， 江蘇 無錫 214122； 2.無錫小天鵝電器有限公司， 江蘇 無錫 214028)

懸掛結構是波輪式洗衣機的重要組成部件，而吊桿作為懸掛結構中的核心部件，其設計參數影響著洗衣機諸多特性。國內外學者對于懸掛系統的研究，主要集中在理論建模[1-3]和動態特性[4-5]等方面。陳海衛等[6-7]建立了波輪式洗衣機振動模型，分析了懸掛系統廣義力，并建立了懸掛系統的空氣動力學模型。劉志鵬[8]建立了懸掛系統在變質量大位移情況下的動力學方程。趙平等[9]研究了洗衣機懸掛系統在不同激振頻率與激振幅值下的動態響應特性，為懸掛系統設計提供了一些理論依據。張華等[10]建立了波輪洗衣機多體動力學平臺，闡述了吊桿的設計方法。但迄今為止，關于洗衣機吊桿懸掛點高度的選擇，尚無系統性的討論分析。課題組通過在MATLAB中建立波輪式洗衣機振動模型，研究了吊桿懸掛點高度對波輪式洗衣機靜力學與動力學特性的影響，明確了吊桿懸掛點高度與洗衣機部分關鍵特性的關系，為深入研究吊桿設計參數準則提供了參考。

1 波輪式洗衣機振動模型

1.1 坐標系的建立

課題組以小天鵝某款波輪式洗衣機為研究對象，該款洗衣機電機采用直驅方式。洗衣機中的液體平衡環會減小洗衣機穩態振幅，但也會增大洗衣機瞬態振幅，本研究主要分析洗衣機本身懸掛結構方面的靜力學與動力學特性，暫不考慮液體平衡環的影響。如圖1所示，波輪式洗衣機主要由外殼、懸掛模塊和工作模塊3部分組成。懸掛系統主要由4根吊桿組成，每根吊桿底部都裝有彈簧阻尼器。為建立波輪式洗衣機的振動模型，創建如圖1所示的2個坐標系：參考系Or-XrYrZr與動系Om-XmYmZm。參考系原點Or固結于大地，Zr軸為洗衣機靜止時盛水桶中心軸線；設吊桿下部與盛水桶的懸掛平面為平面A，則動系原點Om位于Zr軸與平面A的交點。動系相對于參考系的姿態用卡爾丹角[αβγ]T描述。

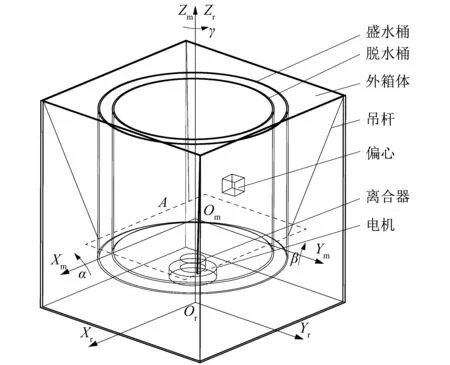
圖1 洗衣機結構及坐標系Figure 1 Structure and coordinate system of washing machine

1.2 盛水桶、電機定子與電機支座的動力學描述

盛水桶、電機定子、電機支座與動系Om-XmYmZm固結，以此類剛體質心建立局部坐標系Od-XdYdZd，為方便計算，以及增減剛體數量，可將所有此類剛體疊加為等效剛體1，則其總動能T1可描述為：

(1)

1.3 脫水桶、電機轉子與波輪的動力學描述

脫水桶、電機轉子與波輪通過旋轉軸與動態坐標系連接，可將該類部件疊加為等效剛體2，則其質心在動系下的位置矢量為：

r2=[0 0h2]T。

(2)

式中h2為等效剛體2質心高度。

則等效剛體2的總動能T2可描述為：

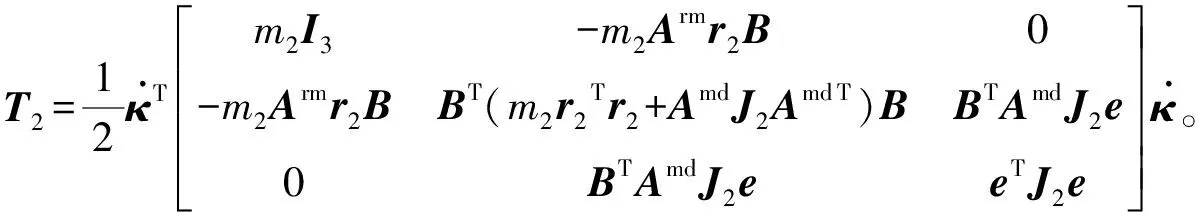
(3)

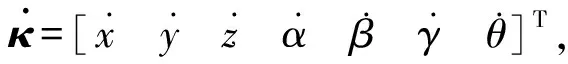
1.4 衣物偏心的動力學描述

忽略慣量，衣物偏心通過旋轉軸與動系連接，其質心在動態坐標系下的矢量位置為：

r3=[R3cosθR3sinθh3]T。

(4)

式中：R3為衣物偏心旋轉半徑；h3為偏心高度；θ為電機旋轉角。

則衣物偏心動能

(5)

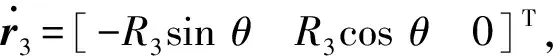
1.5 系統重力勢能的描述

將系統內所有部件的重力勢能相加，可得系統總的重力勢能：

(6)

1.6 廣義懸掛力的描述

波輪式洗衣機懸掛系統由4根吊桿組成。吊桿上下端通過球鉸分別與外箱體、盛水桶連接。根據文獻[11]4根吊桿產生的廣義懸掛力

(7)

式中：Qi，rdi，FDi，MDi分別為第i根吊桿的懸掛力、下懸掛點位置矢量、所受力與力偶。

如圖2所示，盛水桶近似于圓柱體，懸掛結構垂直于盛水桶外壁；L0為彈簧原長；L1為懸掛點下的套筒與底座長度之和；L2為吊桿下懸掛點距盛水桶外壁距離；H為吊桿下懸掛點距地面高度；φ為吊桿傾斜角；R0為吊桿底座半徑；則彈簧壓縮極限

(8)

式中μ為彈簧可壓縮量與彈簧原長的比值。

圖2 吊桿底端懸掛結構Figure 2 Suspension structure at bottom of suspender

1.7 系統整體振動模型

設洗衣機符合直線加速規律，則在洗衣機加速與穩態工作情況下，電機旋轉角θ隨時間的變化關系分別為：

(9)

式中：a為電機角加速度；τ為加速總時間，τ=Ω/a；Ω為洗衣機穩態轉速。

將式(1)，(3)，(5)，(6)和(7)代入第二類Lagrange方程，并去除θ自由度上的描述，得系統總振動方程：

(10)

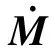
2 洗滌狀態下懸掛點高度對系統靜力學特性的影響

2.1 系統靜力學模型參數

(11)

式中：q*為系統靜平衡位置廣義坐標，其求解可采用Newton-Raphson迭代法：

(12)

式中：

(13)

式中：fg為系統重力勢能Vg對廣義坐標q偏導數。

基于上述理論，在MATLAB中建立仿真模型，模型各類基本參數設置如表1所示。

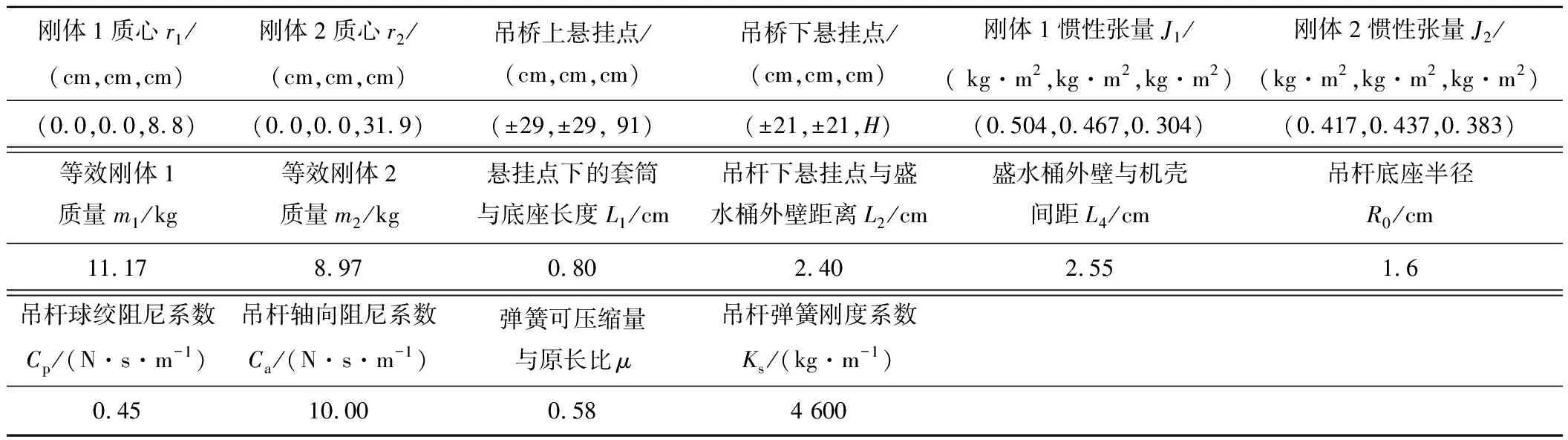
表1 模型基本參數設置

2.2 H對系統靜力學特性的影響

在波輪式洗衣機盛水桶下方，通常裝有電機、離合器、排水閥等部件，且這些部件需與地面保持一定的安全距離，以避免在工作過程中這些部件與地面相撞。本研究中洗衣機吊桿下懸掛點高度H起始最小值設為0.20 m。

洗衣機負載包括衣物與洗滌用水，為對比不同質量負載對洗衣機靜力學特性的影響，設負載總質量分別為0，10和20 kg，且忽略負載產生的偏心。如圖3(a)所示，吊桿傾斜角隨H的增大而快速增大，不同質量的負載會使吊桿傾斜角略微增大。如圖3(b)所示，吊桿彈簧伸縮量隨H的增大而增大，且不同質量的衣物負載對彈簧伸縮量的影響是非線性的。彈簧壓縮量的增大，對彈簧壽命也會造成不利影響，進而影響洗衣機懸掛系統的使用壽命。如圖3(c)所示，吊桿彈簧壓縮極限(公式(8))隨H的增大而快速下降，其與20 kg負載質量下的彈簧壓縮量在0.35 m處相交，如繼續增大H，彈簧壓縮量將超出彈簧壓縮極限。由此可得，在洗滌狀態下，吊桿下懸掛點距盛水桶外壁距離不變，且洗衣機最大負載質量為20 kg時，該款機型吊桿下懸掛點高度H最大值應小于0.35 m。

圖3 H對靜力學特性的影響Figure 3 Influence of H on static characteristics

3 脫水狀態下懸掛點高度對系統動力學特性的影響

3.1 系統動力學模型參數

洗衣機處于脫水狀態時，轉速高且負載質量輕，其動力學特性應是分析重點。設洗衣機穩態轉速Ω為600 r/min，角加速度a為5 rad/s2，衣物偏心質量m3為1 kg，偏心高度h3為0.12 m，旋轉半徑R3為0.21 m，其余模型基本參數參照表1設置。模型仿真過程中，穩態振幅是指洗衣機轉速達到穩態轉速后測得的振幅。

3.2 H對系統穩態振幅的影響

為直觀反映洗衣機盛水桶在脫水過程中的振動情況，故在洗衣機盛水桶外壁上選取了2個測量點：上方測點M與下方測點N。上、下方測量點均位于參考坐標系X軸與盛水桶外測交點，2點高低分布。如圖4(a)所示，為避免懸掛結構先與洗衣機機殼碰撞，結構尺寸應滿足：

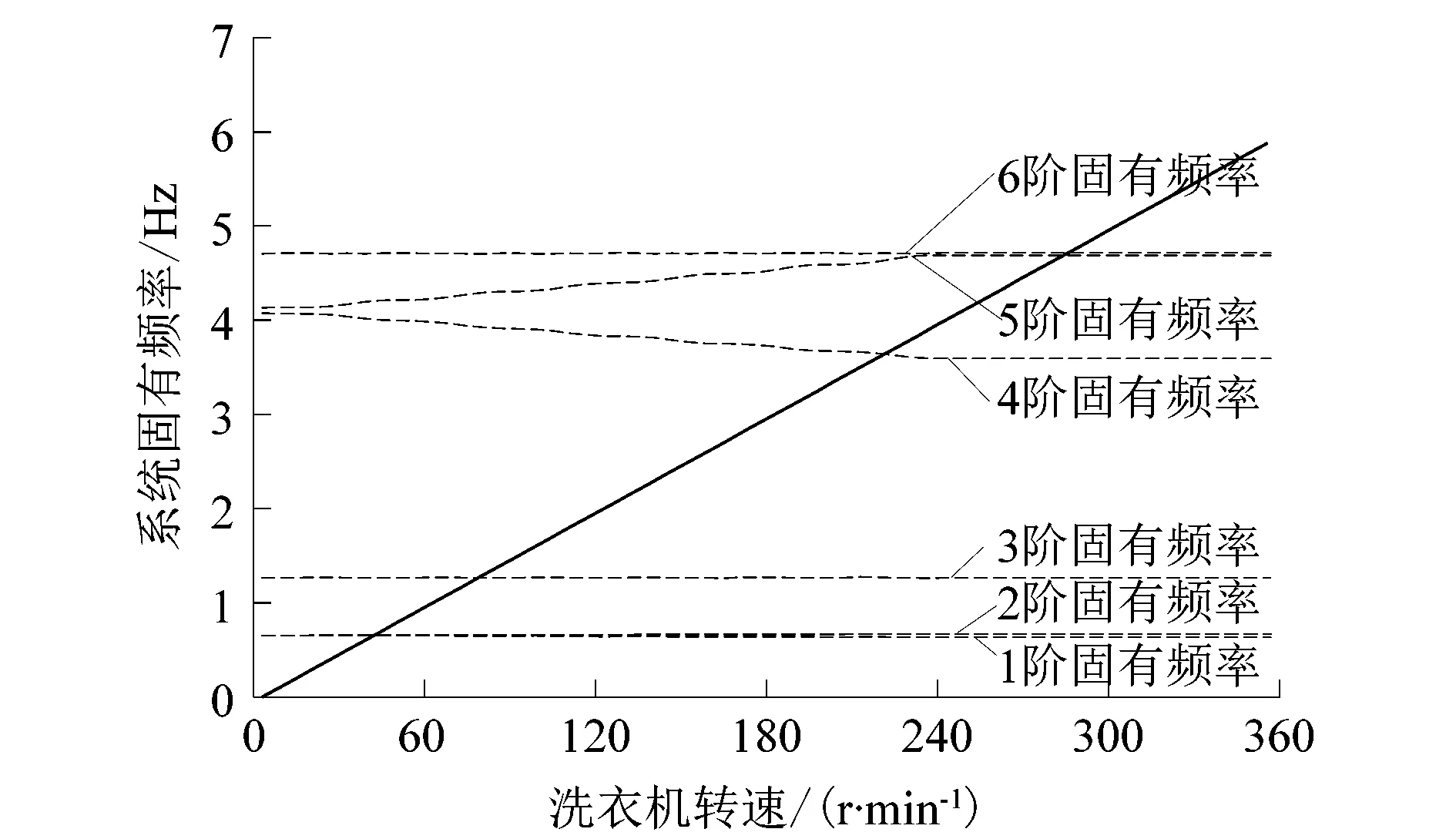
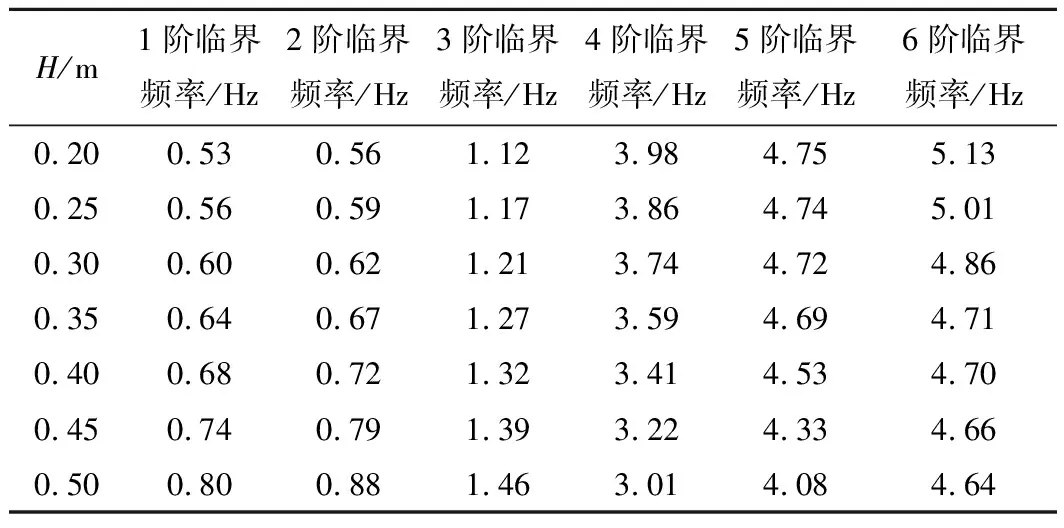
L3

(14)

式中：L3為懸掛結構距洗衣機中軸線的徑向尺寸；R1為盛水桶外壁半徑。

為保證洗衣機在穩態轉速下工作不撞桶，其結構尺寸應滿足：

Am

(15)

式中：Am為盛水桶在穩態轉速下的最大振幅；L4為盛水桶外側與機殼間距，即為盛水桶穩態振幅極限值。

如圖4(b)所示，盛水桶上方測點M與下方測點N的穩態振幅，隨下懸掛點高度H的升高緩慢下降。當高度H>0.28 m后，點M與N的穩態振幅均處于振幅極限值范圍內。由此可得，在脫水狀態下，最大偏心質量m3為1 kg，偏心高度h3為0.12 m，旋轉半徑R3為0.21 m，穩態轉速為600 r/min時，該款機型吊桿下懸掛點高度H最小值應大于0.28 m。

圖4 懸掛結構與H對系統穩態振幅的影響Figure 4 Suspension structure and influence of H on steady state amplitude of system

3.3 H對系統臨界頻率的影響

為了研究波輪式洗衣機吊桿下懸掛點高度H與洗衣機系統臨界頻率之間的關系，將式(10)整理化簡為：

(16)

式中：C為系統總阻尼矩陣；G為陀螺矩陣；K為系統剛度矩陣；f為系統廣義力；n為洗衣機實時轉速。

在吊桿下懸掛點高度H為0.35 m時，洗衣機系統自身的坎貝爾圖如圖5所示。圖5中虛線自下而上分別為系統在各轉速下的前6階固有頻率，過原點的實線為洗衣機轉速對應的固有頻率，實線與虛線的6個交點即為系統前6階臨界頻率。

圖5 H=0.35 m洗衣機系統坎貝爾圖Figure 5 Campbell diagram of washing machine system at H=0.35 m

表2所示為不同吊桿下懸掛點高度情況下，洗衣機系統的前6階臨界頻率。分析可以發現，洗衣機前3階臨界頻率隨高度H增大而逐漸增大，后3階臨界頻率隨高度H的增大而逐漸減小。洗衣機前6階臨界頻率總趨勢是隨高度H的增加而趨于集中。系統臨界頻率過于集中，更易造成共振現象，所以在僅考慮系統臨界頻率時，吊桿的下懸掛點高度H應取較小值。

表2 不同H下的系統臨界頻率

4 結論

課題組通過建立的波輪式洗衣機振動模型，分析了洗衣機吊桿下懸掛點高度H，對不同工作狀態下洗衣機力學特性的影響，得出以下結論：

1) 在洗滌狀態下，下懸掛點高度H增大將引起吊桿傾斜角、彈簧壓縮量的增大，同時降低彈簧壓縮極限。針對此狀態下的靜力學分析，可確定下懸掛點高度H的最大值。

2) 在脫水狀態下，下懸掛點高度H增大使得臨界頻率趨于集中，而洗衣機穩態振幅呈減小趨勢。針對此狀態下的動力學分析，可確定下懸掛點高度H的最小值。

3) 綜合考慮，下懸掛點高度H的選取是一項系統性工程：既要保證洗滌狀態下，吊桿彈簧壓縮量不超過彈簧壓縮極限，從而滿足靜力學要求；又要保證脫水狀態下，洗衣機穩態轉速下的最大振幅不超過振幅極限值，從而滿足動力學要求，并最終確定滿足設計要求的下懸掛點高度H。