軸支架雙槳船附體阻力尺度效應數值分析

韋紅剛 詹明珠 馮 毅 孟 陽 于 海

（1.上海市船舶工程重點實驗室 上海200011；2.中國船舶及海洋工程設計研究院 上海2000113.上海船舶研究設計院 上海201203）

引 言

安裝于水線以下船體表面的附屬體（如側推孔、舵、減搖鰭、軸包套、軸及軸支架等）統稱為船的附體，由于附體的存在而產生的阻力稱為附體阻力［1］。目前比較常見的計算方法是通過全附體與裸船體船模試驗所得到的總阻力的差值來確定附體阻力。但由于船模速度低、附體尺度小，故存在較嚴重的尺度效應［2］。水下附體阻力主要為黏壓阻力和摩擦阻力，雷諾數是其尺度效應的重要影響因素。此外，考慮船尾伴流場的尺度效應是非常必要的，歷屆ITTC會議均十分關注這個問題。第26屆ITTC 伴流場尺度效應專門委員會［3］還系統地總結了目前存在的幾種換算法。

CFD就是針對目標船型利用計算機進行數值計算，從而得到船舶阻力等的計算方法。CFD是船舶計算流體力學的一個分支，也是船舶流體力學最基本的應用［4］。目前理論上進行實尺度船舶附體數值計算已經成為可能，只是缺乏實船驗證數據［5］。

目前國內外已有眾多學者對船舶尺度效應開展了相關研究。張恒和詹成勝［6］計算了KCS（KRISO Coutainer Ship；其中： Korea Research Institute for Ships and Ocean Enginearing，KRISO）在不同雷諾數下的阻力值，證明通過改變介質的黏性系數使得不同尺度船舶滿足全相似是可行的。陳騫等［7］計算了靜水下實尺度船舶不同航速的總阻力，并通過水池試驗驗證了實尺度模擬、優化的可行性。王展智和熊鷹［8］計算了DTMB5415多種尺度的船舶黏性流場，詳細分析了該船軸向伴流場的尺度效應。Bart Schuiling［9］采用數值方法研究了伴流場的尺度效應。李亮和王超［10］開展了KCS考慮自由液面的實船自航試驗數值模擬。

本文采用CFD商用軟件NUMECAFineMarine數值模擬，基于RANS（Reynolds Average Navier-Stockes）方法，采用 VOF（Volume of Fluid）方法捕捉自由液面，通過采用動網格剛性變形結合加權變形來處理船舶直航引起的升沉和縱傾浮態變化［11］；開展了軸支架雙槳船附體尺度效應數值模擬并與模型試驗及其實船換算結果對比，分別分析了側推孔、軸包套、軸支架阻力性能及附體壓力分布的尺度效應；同時簡要分析了軸支架雙槳船的自由液面波形和軸向伴流尺度效應。

1 數學模型和數值方法

取尾垂線和基平面交點為原點，從船尾指向船首為x方向，船寬左舷方向為y方向，z方向垂直向上，形成右手坐標系，見圖1。

圖1 坐標系和計算模型

對于非定常、不可壓的黏性流體，采用流動的控制方程為RANS方程：

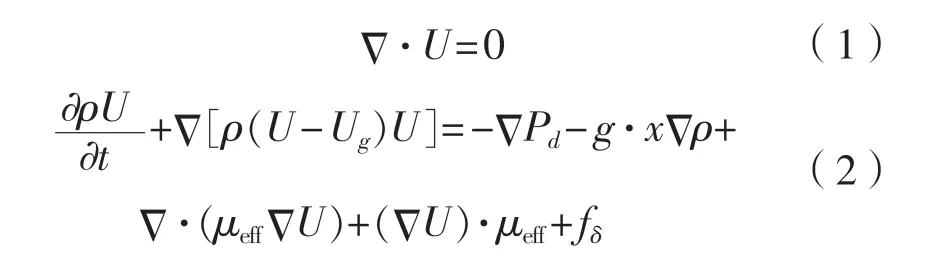
式中：U和Ug分別為流場速度和網格節點速度，m/s；Pd為流場動壓力，Pa；μeff為動力黏性系數；fδ為表面張力，N/m3。

2 模型尺度數值模擬及試驗驗證

本文以某型軸支架雙槳船為研究對象，采用計及姿態的阻力和伴流數值模擬方式，數值模擬并分析了軸支架雙槳船型阻力與伴流尺度效應分析。表1為某型軸支架雙槳船部分船模主尺度。

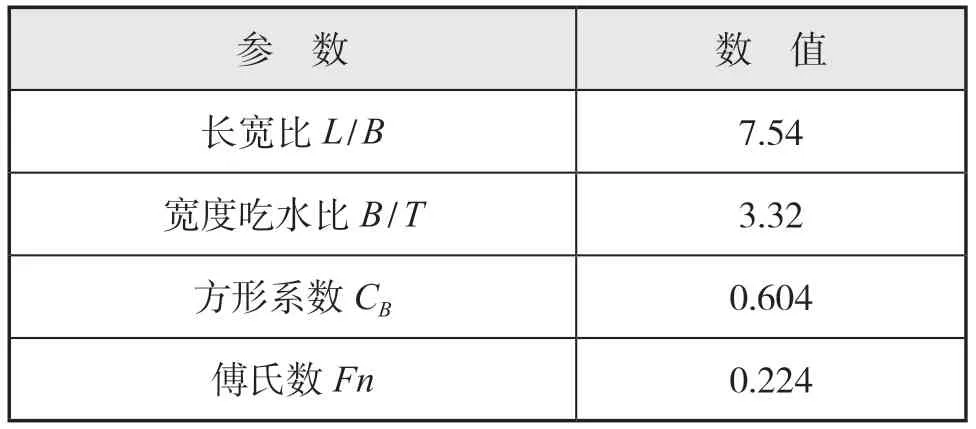
表1 船模A主尺度

針對阻力數值模擬，在HEXPRESS軟件中生成高質量六面體非結構化網格，整個計算域與船體表面網格如圖2所示。

圖2 計算域及船體表面網格

計算設置船體縱傾和沉降為自由變化，輸入船體浮心坐標（以浮心替代重心作為轉動中心）、重力、繞y軸的慣性矩［12］。

該計算域的長度為5倍船長，寬度為1.5倍船長，高度為1.5倍船長。

在側推孔、支架、舵等附體采用逐層細化的全六面體非結構網格生成技術，并在側推孔、支架、舵等附體表面采用拆分緊鄰物面一層網格單元的方法生成適當層數的邊界層網格［11］。

首先對該軸支架雙槳船進行靜水中的裸船體和全附體（包括側推孔、軸包套、支架、舵等附體）阻力數值模型模擬和試驗驗證，模型試驗照片見圖3。

圖3 模型試驗照片

模型尺度（雷諾數Re=1.1×107）阻力計算和模型試驗換算成實船的有效功率Pe對比結果見下頁圖4。

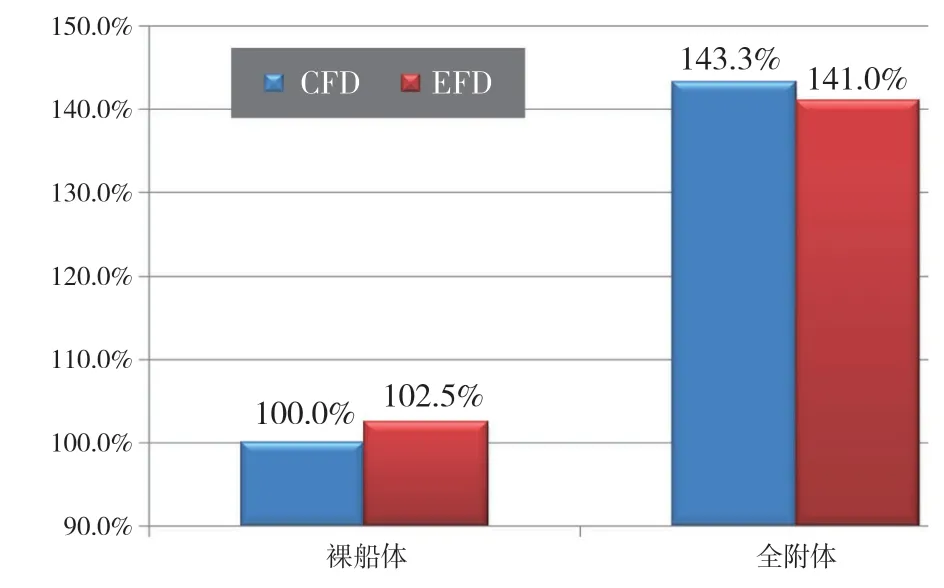
圖4 船模計算與試驗Pe對比

可見，無論是裸船體還是全附體計算，均與試驗結果吻合良好，故可以此計算方法為基礎，考慮尺度效應的數值模擬與分析。由于該軸支架雙槳船附體種類和數量多，因此其全附體阻力的增量偏大。本文中的阻力增量百分比均為與CFD計算中雷諾數為1.1×107時裸船體有效功率之比的增量。

在模型尺度裸船體和全附體數值模擬的基礎上，通過改變船模長度的方法，本文分別對“裸船體”、“裸船體+側推孔”、“裸船體+側推孔+軸包套”、“裸船體+側推孔+軸包套+支架”進行了不同雷諾數下的模型數值模擬，并進行附體阻力增量尺度效應分析。

3 阻力、附體壓力分布尺度效應分析

本文對不同尺度的阻力、伴流數值模擬生成不同厚度的邊界層。表2為不同雷諾數（Re）時的Y+，圖5為船體模型尺度流線圖。從圖5可見，船體表面流動順暢，無明顯的流動分離和匯聚現象，從而為不同附體阻力增量的尺度效應分析提供良好的基礎。

圖5 船體流線圖

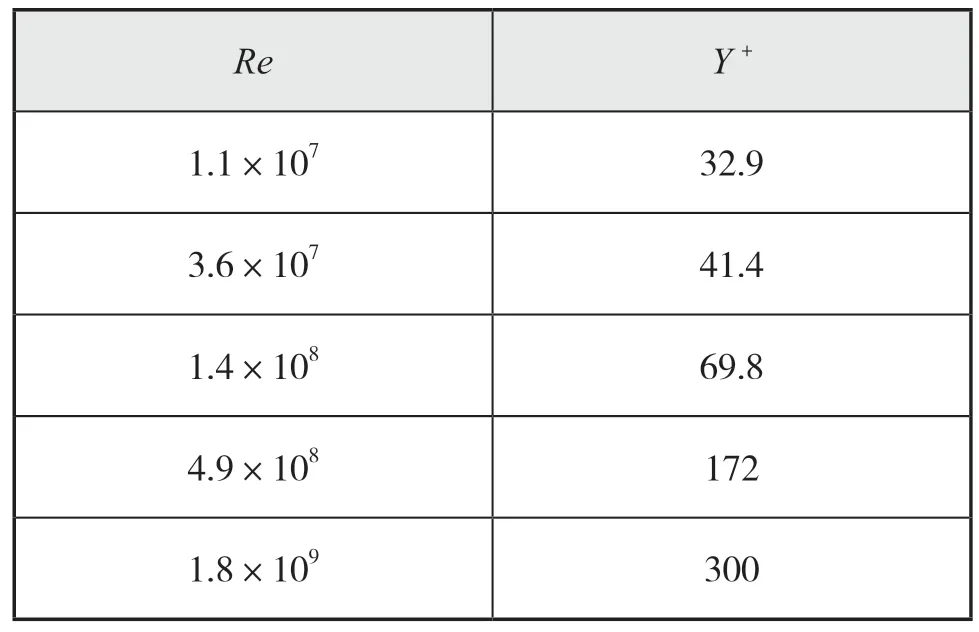
表2 不同Re下的網格Y +

圖6為不同Re阻力數值模擬結果對比；下頁圖7為不同Re下各附體Pe增量對比。不同尺度的數值模擬都采用淡水的密度和黏度，同時并沒有在數值模擬中考慮表面粗糙度的差異，而是在換算過程中統一標準補償此差異。

圖6 不同Re阻力數值模擬結果對比

從圖6和圖7中可見，無論是裸船體還是裸船體+附體阻力計算，Pe結果均隨Re的增加而增大。這一增量在Re為107量級上最快，隨后趨于平緩。3種附體的阻力增量均不隨Re的增加而單調變化，但在Re＞108以后基本趨于穩定。側推孔和軸包套隨Re增加，但阻力增量變化很小，均在1%以內；軸支架的阻力增量在Re為107～108時，與裸船體相同，增加均很快。

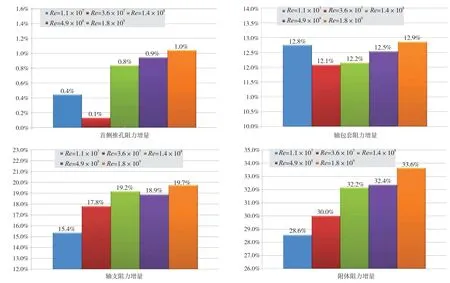
圖7 不同Re的附體Pe增量對比

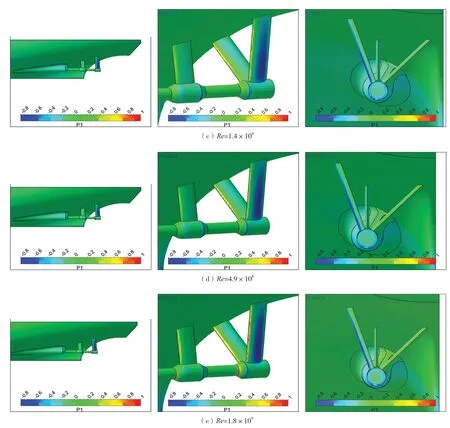
續圖8 不同附體壓力分布數值模擬結果

下頁圖8為軸包套和支架不同Re下的無量綱壓力分布。從圖中可見，軸包套折角處收縮較為劇烈，此處存在一個負壓較大的區域；且這一區域的面積和絕對數值均隨Re增加而明顯增大。雙臂外支架的外側處大片的負壓區域是支架阻力增量很大的原因，當Re為107～ 108時，負壓區域面積增加明顯。這與圖7中支架阻力增量隨Re變化關系相對應。

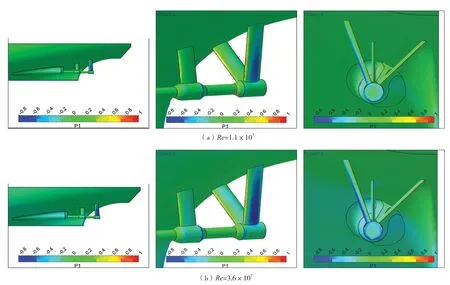
圖8 不同附體壓力分布數值模擬結果

4 興波、伴流尺度效應分析

在阻力尺度效應分析的基礎上，進一步開展軸支架雙槳船興波和伴流的尺度效應分析。下頁圖9為“裸船體+側推孔+軸包套+支架”在不同雷諾數無量綱自由液面的數值模擬結果。由圖9可見：不同雷諾數船體中前部分的興波差異很小，這同興波阻力與Re無關的假設相符，但在船尾后方波形存在一定的差異，這與船體傅氏數及尾封板浸水深度相關。

圖9 不同Re自由液面數值模擬結果

下頁圖10為不同Re槳盤面（0.35R～1.2R）伴流數值模擬結果（左舷）。由圖10可見，軸向伴流順時針30°區域存在一片伴流較高的區域，可能是后視圖中包套和內支架聯合影響的結果。高雷諾數數值模擬結果表明：高伴流區域的伴流峰值顯著降低，其他低伴流區域面積隨著Re的升高顯著增大。

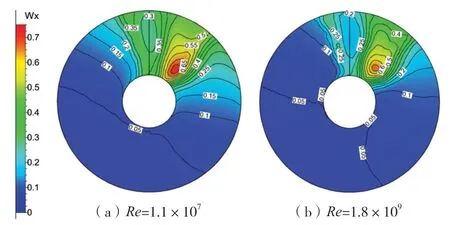
圖10 不同Re伴流數值模擬結果（左舷）

5 結 論

本文使用NUMECAFineMarine軟件研究軸支架雙槳船尺度效應，研究發現：

（1）由于附體區域的局部Re遠遠小于船體Re，當船體Re大于108之后，3個附體的阻力增量才基本穩定。為了減小尺度效應影響，軸支架雙槳船模型試驗的Re應盡可能大些。

（2）不同Re船體中前部分的興波差異很小，但在船尾后方波形存在一定差異。這與船體傅氏數及尾封板浸水深度相關。對于軸支架雙槳船，槳盤面軸向伴流均值和伴流峰值都隨Re增加而降低。