基于ABM 器件的SiC MOSFET 建模研究

王迪迪 ,寧平凡 ,劉 婕 ,張永剛

(1.天津工業大學 電氣工程與自動化學院,天津 300387;2.天津工業大學 電子與信息工程學院,天津 300387;3.大功率半導體照明應用系統教育部工程研究中心,天津 300387)

SiC MOSFET 以其耐高溫、工作頻率高和功率損耗低等優勢,具有廣泛的應用前景[1-3]。由于精確的器件模型是電路設計和系統開發的基礎,SiC MOSFET 的建模研究逐漸成為科研人員關注的熱點。國內外研究學者提出許多模型,其中薩支唐等提出的MOS 晶體管模型[4]和北卡羅來納州立大學王軍等提出的變溫參數模型[5]具有普遍的指導意義,隨后衍生出變溫參數改進模型、開關損耗模型和等效電路模型[6-9]等。然而大多都是在恒溫下基于Cadence 軟件對器件進行建模研究,對于模型在溫度變化方面的研究仍有不足,特別是溫度變化對閾值電壓和導通電阻的影響研究。

目前許多新型SiC MOSFET 器件并沒有可以直接使用的仿真模型,需要自行建模才能對其開展仿真研究[10-11]。PSpice 軟件具有功能強大、元件庫多和仿真接近真實等優點,成為研究器件模型的主要工具[7]。其自帶的Model Editor 可直接建立SiC MOSFET 模型,但該模型存在閾值電壓不隨溫度變化的問題,對變溫下器件的開關過程模擬不準確。

為了建立更為精確的模型,本文提出一種基于ABM 器件建立的SiC MOSFET 模型,該模型基于薩支唐方程進行改進[4,12],引入閾值電壓和跨導系數的溫度調節函數建立溝道電流模型,基于壓控電阻原理引入溫度和柵源電壓建立溫壓導通電阻模型,利用ABM器件的函數編輯功能,取代壓控開關器件建立無開關壓控柵漏電容模型[13-16]。通過對這三個部分的改進,建立了更為精確的SiC MOSFET 模型,對模擬高溫高頻下器件的開關過程有重要意義,并對建模具有一定的借鑒意義。

1 SiC MOSFET 模塊化建模

本文將整體模型分為溝道電流、內部電阻、極間電容和體二極管4 個部分分別建模,其結構如圖1 所示[3]。建模思路是對SiC MOSFET 模型的溝道電流、導通電阻、柵漏電容三個部分進行改進;通過Origin軟件處理數據表的曲線,得到相應的數字化數據;利用1STOPT 軟件對改進后的模型公式擬合編程,提取模型參數;使用PSpice 軟件中的ABM 器件完成模型的搭建[14],以打包子電路的方式建立模型。SiC MOSFET 模塊化建模思想及流程如圖2 所示。

圖1 整體模型結構圖[3]Fig.1 Overall model structure diagram[3]

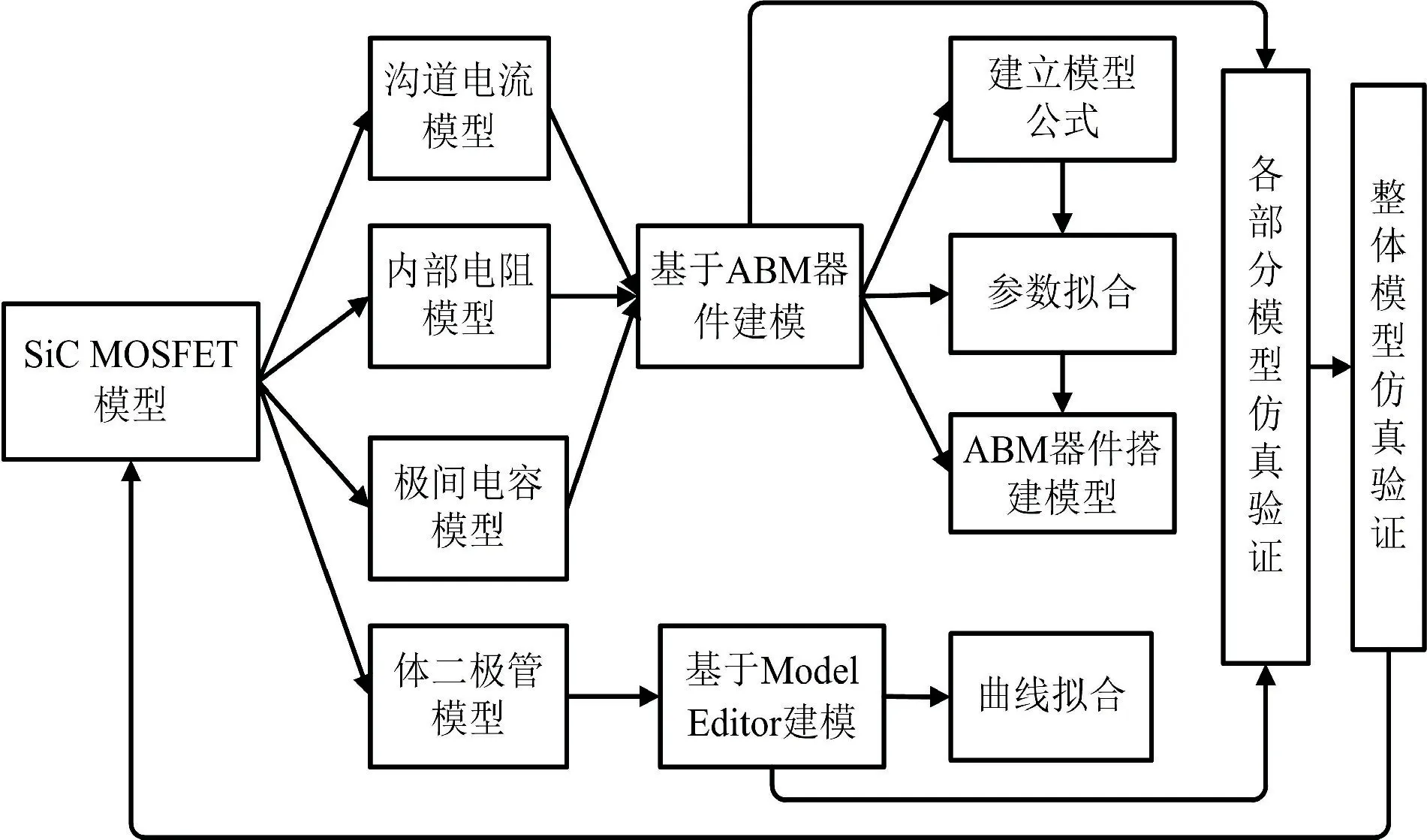
圖2 SiC MOSFET 模塊化建模思想及流程Fig.2 SiC MOSFET modular modeling ideas and processes

1.1 溝道電流模型改進

通過在薩支唐方程的基礎上進行改進后,采用電壓控制電流源模擬溝道電流的工作特性,建立溝道電流模型。薩支唐方程如式(1)所示,由于溝道長度L、溝道寬度W都是定值,改進后采用一個模型參量KPnom進行擬合[4,8];考慮到跨導系數的負溫度關系,引入溫度調節函數見式(2);依據數據表可知閾值電壓隨溫度的升高而減小,引入閾值電壓的溫度調節系數見式(3);最終建立改進后的溝道電流模型,如式(4)所示。

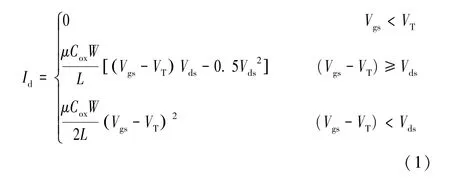
式中:μ為載流子的遷移率;Cox為單位柵電容大小;W和L分別為溝道寬度和長度;VT為閾值電壓。

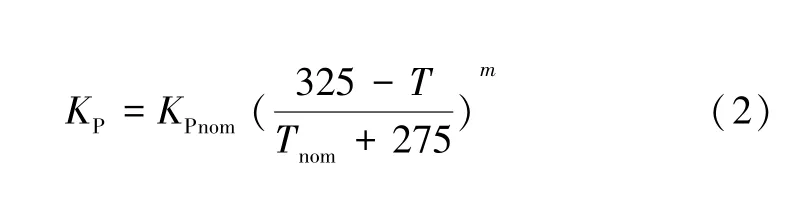
式中:KP為跨導增益變量;KPnom為室溫25 ℃下的跨導擬合參數;Tnom代表室溫;T為仿真溫度。

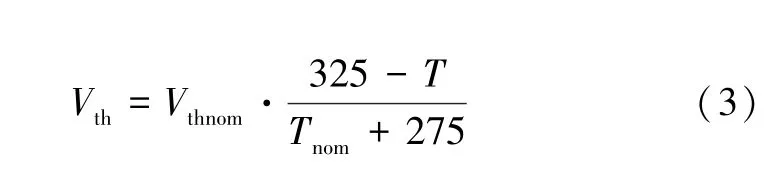
式中:Vth為閾值電壓;Vthnom為室溫下的閾值電壓擬合參數。

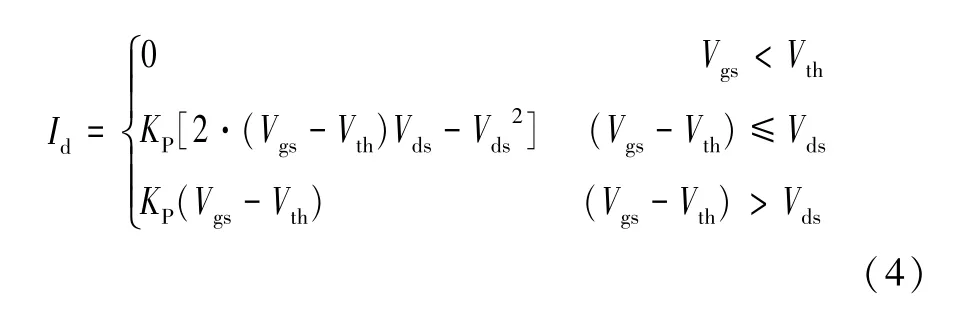
依據數據表中提供的靜態特性曲線,使用擬合軟件對模型公式進行編程,即可得到溝道電流模型的相關參數,模型參數擬合結果如表1 所示。與使用建模工具Model Editor 建立的模型相比,省去了大量的數據處理和參數(L、W、Cox等)提取過程,只需要依據數據表提取KPnom、Vthnom和m參數即可,參數少使得模型建立更加便捷簡單,同時優化了模型仿真的收斂性。更重要的是解決了閾值電壓不隨溫度變化的問題,使建立的模型更加精確。

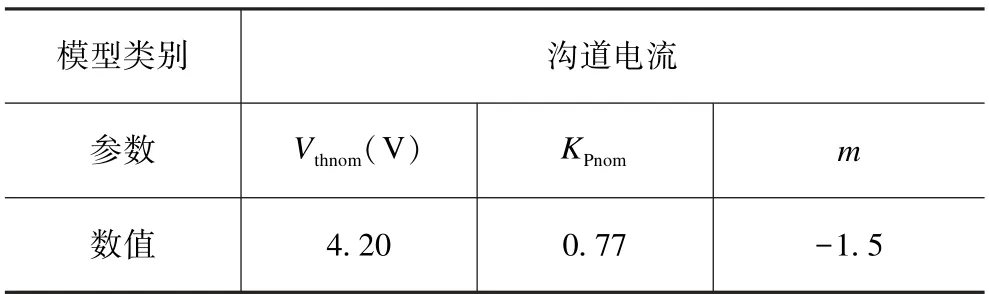
表1 溝道電流模型參數擬合結果Tab.1 Channel current model parameter fitting results

1.2 溝道電流模型改進

導通電阻模型通常直接使用定值電阻對其進行模擬,也有使用PSpice 軟件中的Rbreak 電阻(考慮了溫度參數)進行建模。由數據表可知Rds_on既與溫度有關,隨溫度的上升而增大,也與柵源電壓Vgs有關,隨Vgs的增大而減小。其不能精確地模擬導通電阻的真實情況,使得器件的開關損耗和靜態特性不準確。

為了建立更為精確的導通電阻模型,本文對壓控電阻模型[14,17-18]進行改進,引入溫度和柵源電壓參數建立溫壓導通電阻模型。根據數據表中提供的Rds_on-T曲線,建立R(T)的二階溫度函數,如式(5)所示;根據數據表中提供的Rds_on-Vgs曲線,建立R(V)的指數函數,如式(6)所示。聯合這兩個函數可得到導通電阻的模型公式,如式(7)所示。依據數據表提供的Rds_on-T和Rds_on-Vgs曲線數據,使用擬合軟件對模型公式進行編程,得到溫壓導通電阻模型的相關擬合參數,結果如表2 所示。

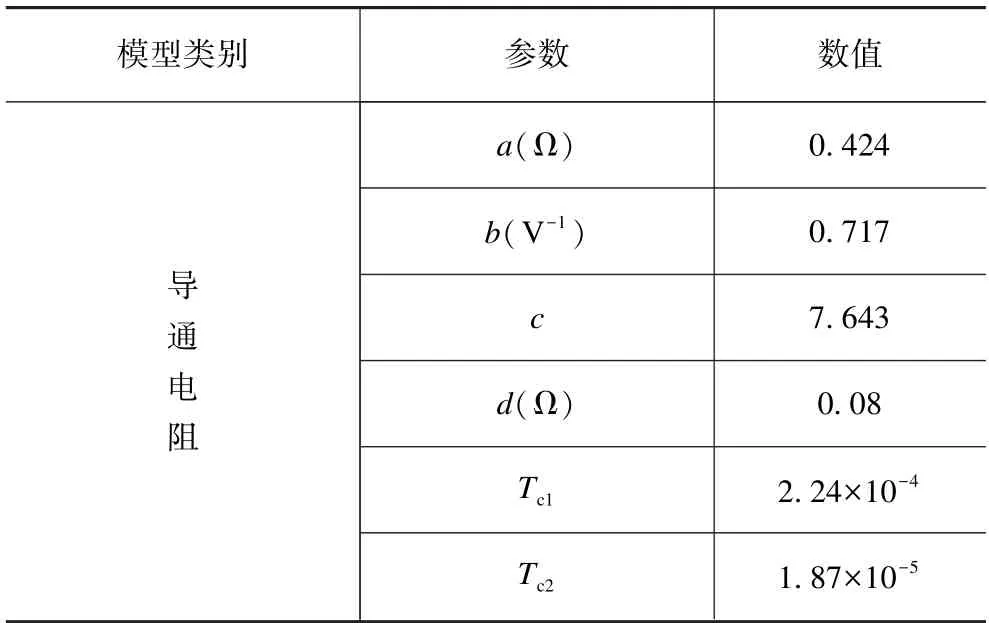
表2 導通電阻模型參數擬合結果Tab.2 On-resistance model parameter fitting result table

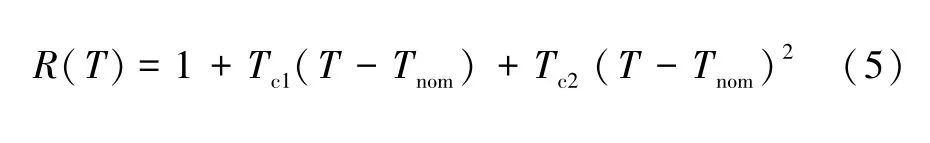
式中:T為工作溫度;Tc1和Tc2分別為一次和二次溫度系數。

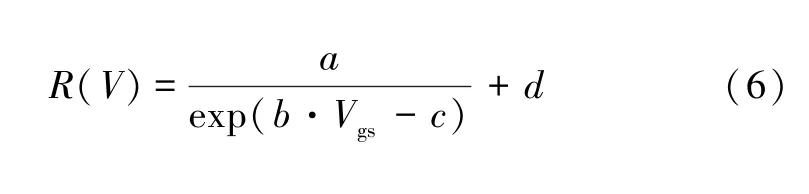
式中:a、b、c、d為壓控電阻的模型參數,只有數值含義。

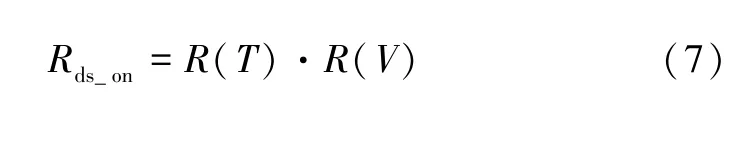
1.3 柵漏電容模型改進

模型的極間電容包括柵漏電容Cgd、漏源電容Cds和柵源電容Cgs,而柵源電容Cgs視為定值電容直接建模,為了避免Cds的重復建模,將其與體二極管Db的結電容聯合建模[18-19]。因此本節主要對柵漏電容進行改進建模。

SiC MOSFET 器件的Cgd模型主要有兩類,包括開關電容模型和組合電容模型[3,9]。其原理都是以柵漏電壓Vgd的正負為判斷依據,當Vgd>0 時,將Cgd作為一個定值電容來建模;當Vgd<0 時,Cgd的容值會隨著漏極電壓的增大而減小,是一個非線性的函數關系[18]。其區別是對兩條支路的電容選擇的方式不一樣,前者使用壓控開關器件實現不同電容的切換,后者利用PN結的通斷進行選擇。

本節對壓控開關電容模型進行改進,利用ABM器件優秀的函數編輯功能,直接使用函數語句選擇不同支路的電容,建立非線性無開關壓控柵漏電容模型,如式(8)所示。該模型巧妙地利用絕對值函數和IF 語句代替了開關器件,減少了開關器件和節點數量,在一定程度上解決了由節點過多帶來的仿真不收斂問題。

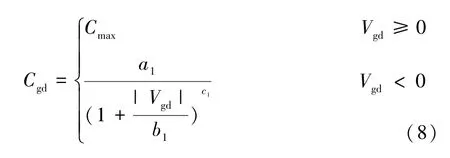
式中:a1、b1、c1為Cgd模型參數,只有數值大小。

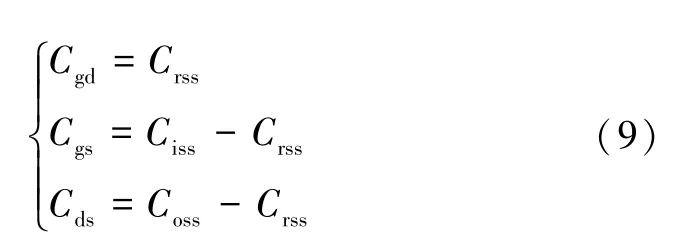
式中:Ciss為輸入電容;Coss為輸出電容;Crss為反向傳輸電容。

根據數據表中提供的輸入電容Ciss、輸出電容Coss和反向傳輸電容Crss的曲線信息,利用極間電容與其滿足式(9)的關系,得到柵漏電容與Vgd的曲線關系。經過對Crss曲線的數據擬合,得到的模型參數,如表3所示,其中參數a1與Cmax大小相等,說明分段處連續。

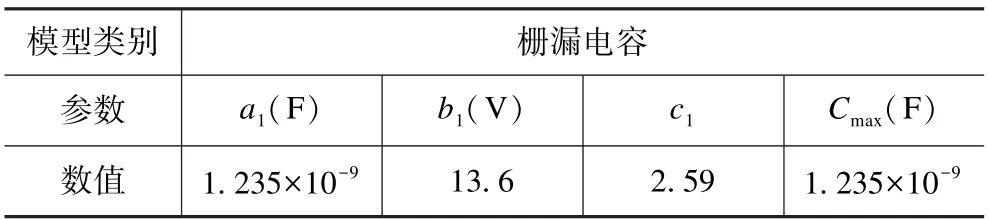
表3 柵漏電容模型參數擬合結果Tab.3 Fitting results of gate-drain capacitance model parameters

1.4 體二極管建模

由于SiC 二極管和Si 二極管的特性差異不是很大,本文使用軟件自帶的建模工具Model Editor,結合數據表提供的體二極管信息直接建立二極管模型。

2 模型搭建與仿真驗證

2.1 溝道電流模型搭建與驗證

依據改進后溝道電流模型公式,使用ABM 庫里的器件對模型公式進行編輯,采用電壓控制電流源EVALUE器件[16,20],實現溝道電流的功能,最后采用打包子電路的方式建立溝道電流模型,其模型如圖3 所示。

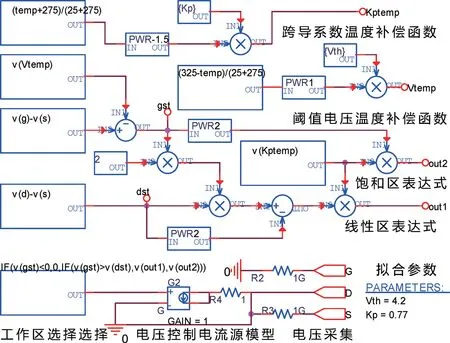
圖3 溝道電流模型Fig.3 Channel current model

搭建溝道電流模型的靜態仿真電路,驗證模型的靜態特性(轉移特性和輸出特性)。其中轉移特性仿真設置為:Vds為定值20 V,溫度分別為25 ℃和135 ℃,直流掃描Vgs在0～20 V 內變化,轉移特性仿真結果如圖4 所示;輸出特性仿真設置為:室溫25 ℃,在不同電壓Vgs(10～20 V)下,直流掃描Vds在0～20 V 內變化,輸出特性仿真結果如圖5 所示。

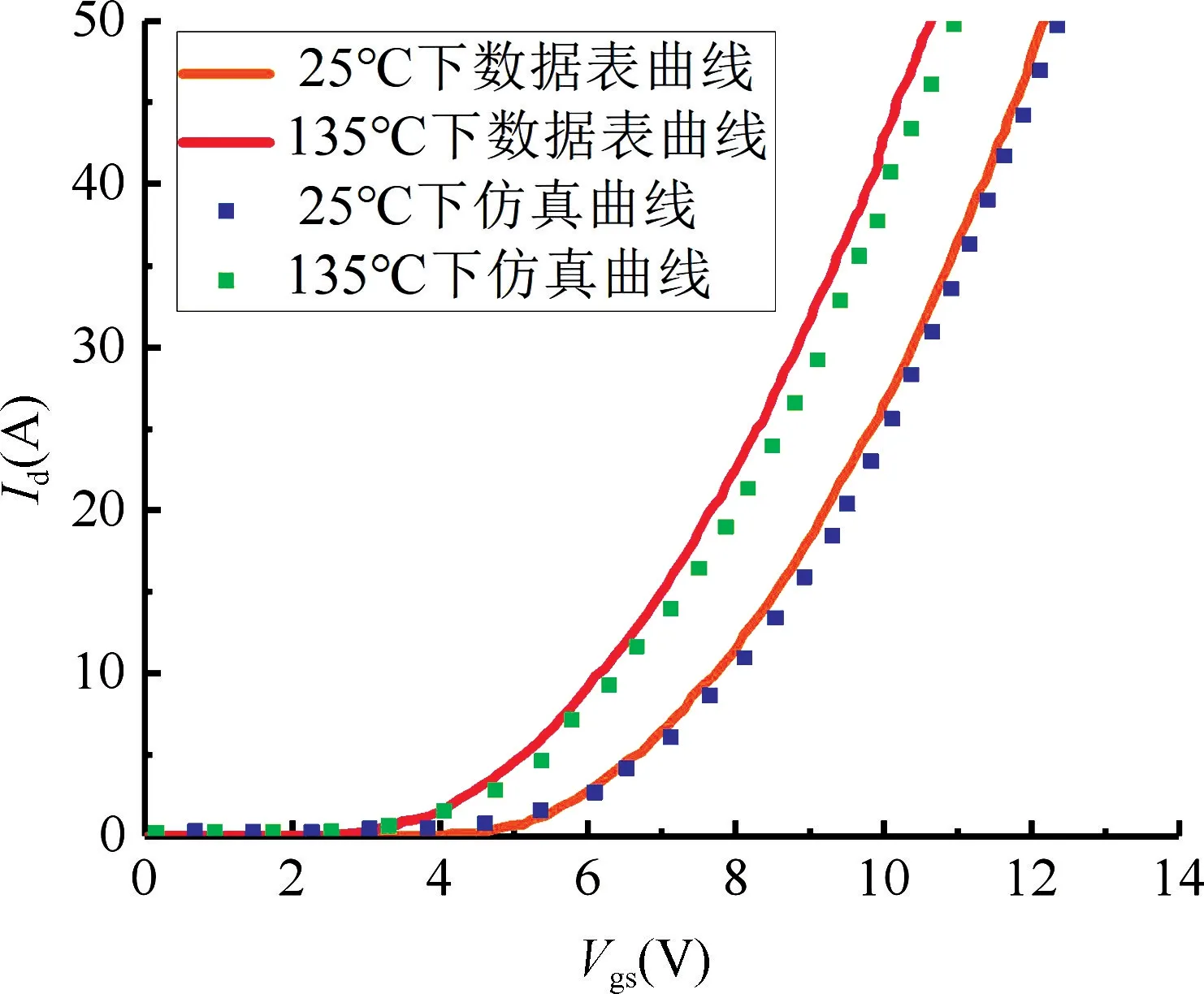
圖4 轉移特性仿真結果Fig.4 Simulation results of transfer characteristics

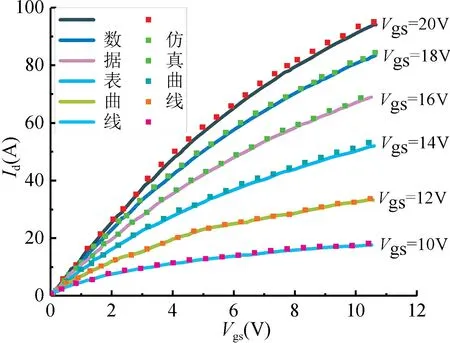
圖5 輸出特性仿真結果Fig.5 Output characteristic simulation results

通過將仿真結果與數據表對應曲線對比,顯示出一致性,表明該模型修正了溫度對跨導系數和閾值電壓的影響,驗證了溝道電流模型的準確性。

2.2 導通電阻模型搭建與驗證

導通電阻的模型使用壓控電阻模型進行建模。根據數據表中提供的Rds_on-T和Rds_on-Vgs曲線數據,利用ABM 庫里的器件將R(T)與R(V)表示出來,以電壓的形式輸出給壓控電阻的控制端,用于控制電阻值的大小,從而建立溫度與Vgs聯合控制的導通電阻模型,搭建結果如圖6 所示。

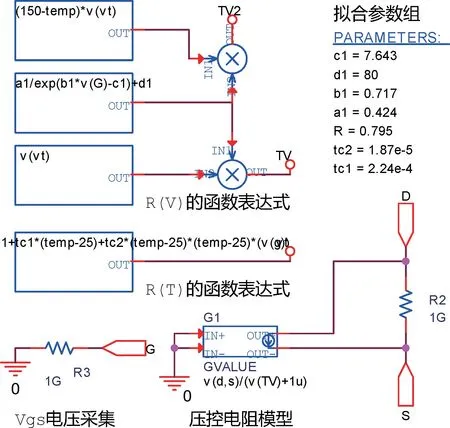
圖6 導通電阻模型Fig.6 On-resistance model circuit diagram

搭建導通電阻模型的仿真實驗電路,驗證模型是否滿足壓控以及溫控功能。在25 ℃下掃描柵源電壓Vgs建立仿真,得到不同Vgs下導通電阻仿真結果,如圖7 所示;在25 ℃和135 ℃下掃描Vgs建立仿真,得到不同溫度下的導通電阻仿真結果,如圖8 所示。仿真與數據表對比的結果表明:本文建立的壓控電阻模型能夠滿足溫度的關系,具有良好的溫控特性和壓控特性,可以很好地反映溫度變化對電阻的影響,驗證了導通電阻模型的準確性。

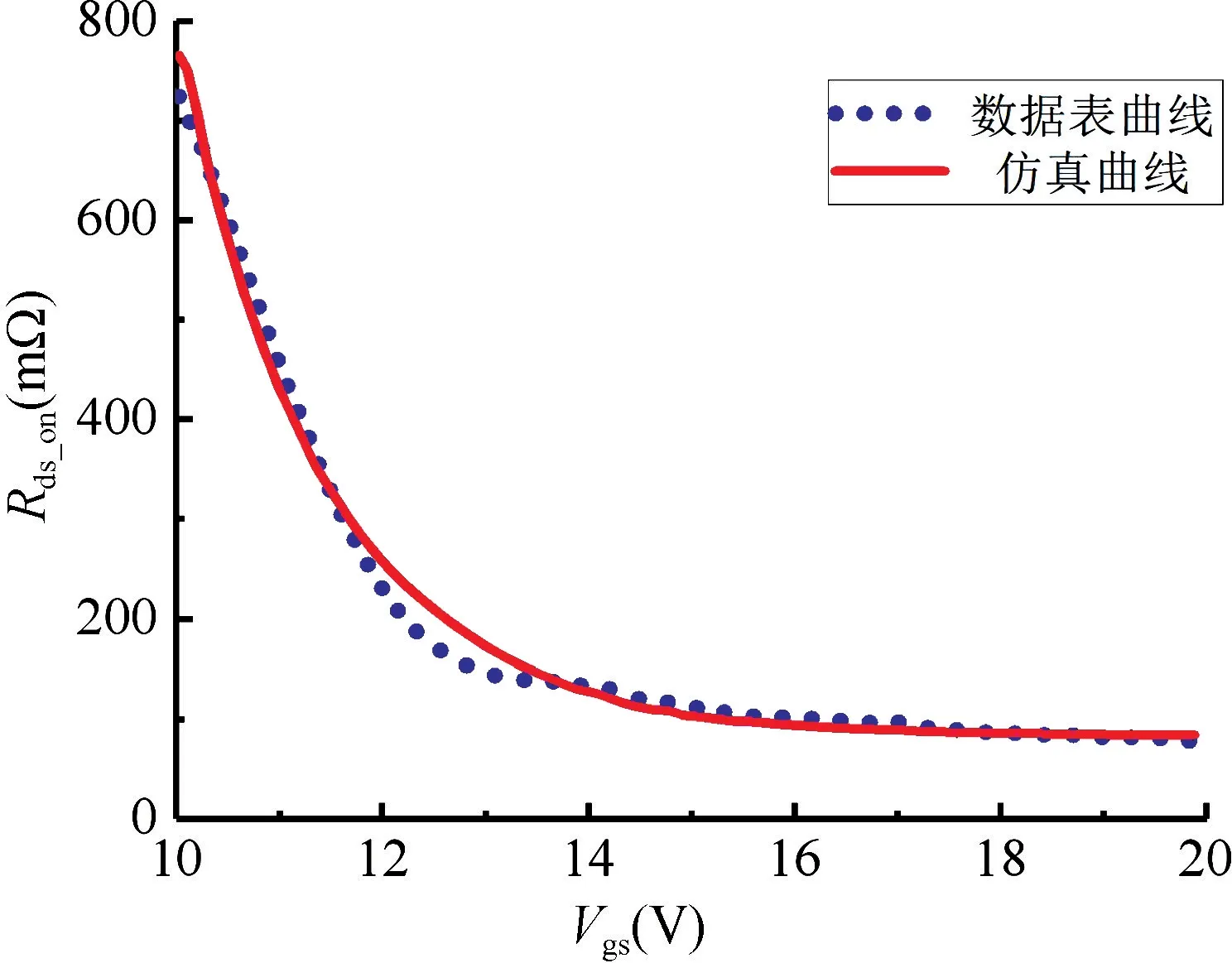
圖7 不同Vgs下導通電阻仿真結果Fig.7 Simulation results of different Vgs on-resistance

圖8 不同溫度下導通電阻仿真結果Fig.8 Simulation results of on-resistance at different temperatures

2.3 柵漏電容模型搭建與驗證

依據上述原理搭建Cgd模型,通過使用ABM 器件,結合函數語句控制模型的開關,實現開關電容Cgd的功能,建立如圖9 所示的柵漏電容模型。

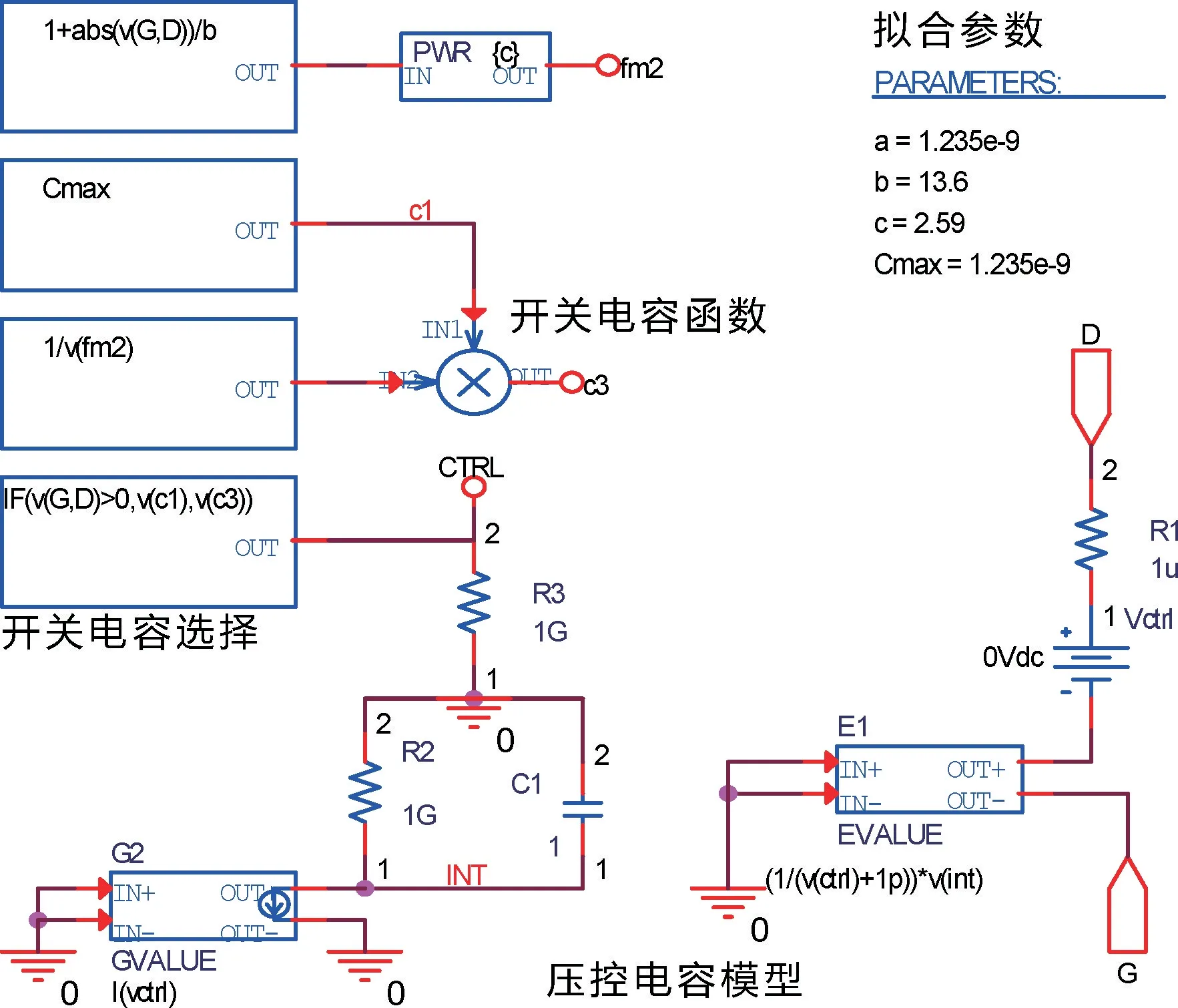
圖9 柵漏電容模型Fig.9 Gate-drain capacitor model

搭建Cgd模型的仿真測試電路,通過在柵極和漏極之間施加-200～40 V 電壓,測量節點CTRL(見圖9)處的電壓值,驗證Cgd模型的壓控功能,仿真結果如圖10 所示。

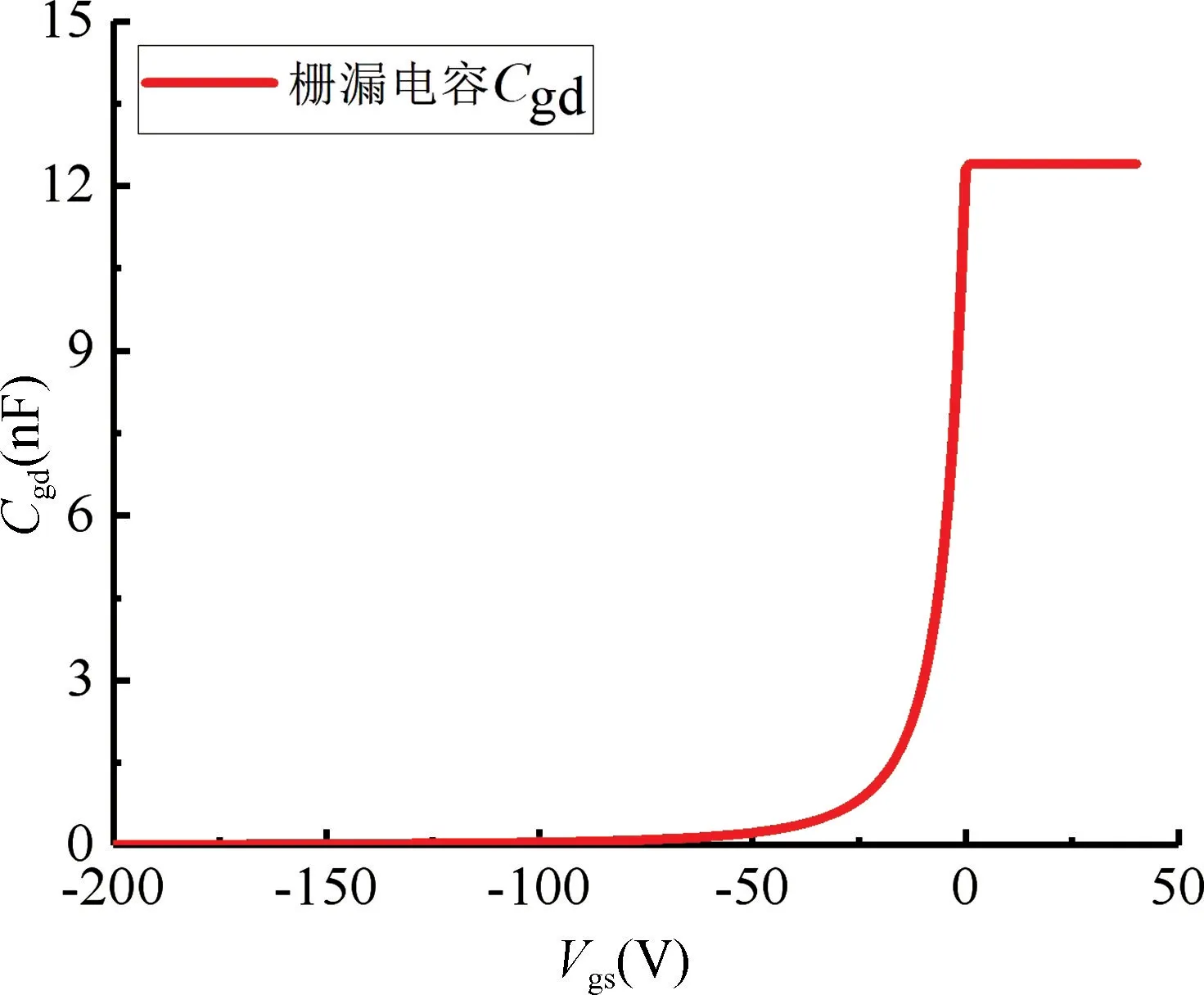
圖10 柵漏電容仿真結果Fig.10 Gate-drain capacitance simulation results

仿真結果表明:柵漏電容的模型,在Vgd>0 時,為一個恒定電容;在Vgd<0 時,容值隨Vgd的增大而非線性地減小,可以實現開關電容的功能,結果與原理分析一致,驗證了模型的準確性。

2.4 整體模型仿真驗證

將上面建立的各部分模型進行組合搭建SiC MOSFET 的整體模型,并搭建整體模型雙脈沖仿真電路[15](如圖11 所示),驗證整體模型的準確性。通過測量雙脈沖仿真電感電流IL1的仿真結果(如圖12 所示),驗證體二極管的續流特性;通過測量雙脈沖仿真體二極管電壓VDb的仿真結果(如圖13 所示),驗證整體模型的開關特性。

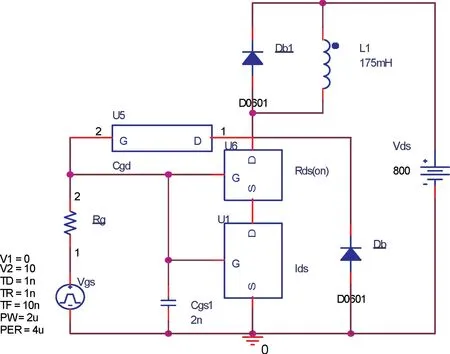
圖11 整體模型雙脈沖仿真電路圖Fig.11 Overall model double pulse simulation circuit diagram

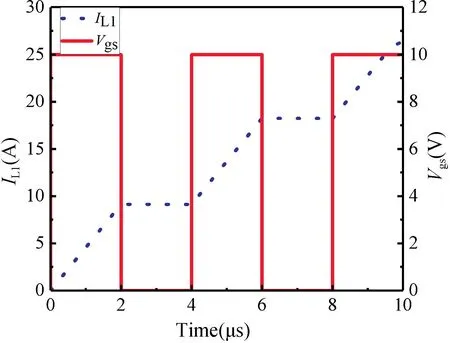
圖12 雙脈沖仿真IL1仿真結果Fig.12 IL1 simulation results of double pulse simulation

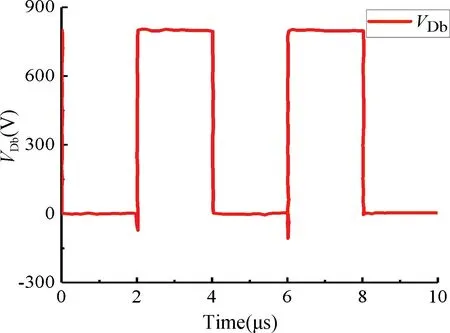
圖13 雙脈沖仿真VDb仿真結果Fig.13 VDb simulation results of double pulse simulation

仿真結果表明:SiC MOSFET 模型能夠準確地模擬器件開關,當器件第一次導通時,電感電流IL1逐漸增加;當其關斷時,由于體二級管Db 的續流作用,IL1的大小和方向維持不變;當其第二次導通時,IL1在第一次的基礎上繼續增大。理論與仿真結果對應,說明整體模型的準確性。

3 結論

本文基于ABM 器件建立了一種適應溫度變化的SiC MOSFET 模型。該模型從三個方面進行了改進,首先針對閾值電壓不隨溫度變化問題,引入閾值電壓與跨導系數的溫度調節函數建立溝道電流模型;然后針對傳統模型沒有考慮柵源電壓對導通電阻的影響問題,引入溫度和柵源電壓聯合參數建立導通電阻模型;最后利用ABM 器件的函數編輯功能,建立無開關柵漏電容模型。并且搭建各部分模型和整體模型的仿真電路,將仿真結果與數據表數據進行對比,驗證本文模型的準確性。該模型省去了壓控開關器件,減少了節點數量,在一定程度上解決了模型由于節點過多導致的仿真不收斂問題,并簡化了模型,對器件建模具有一定的借鑒意義。