高速鐵路軌道靜態幾何不平順弦測評價標準體系研究

楊飛 劉丙強 譚社會 馬文靜 時瑾 孫加林

1.中國鐵道科學研究院集團有限公司基礎設施檢測研究所，北京100081；2.中國國家鐵路集團有限公司工電部，北京100844；3.中國鐵路上海鐵路局集團有限公司，上海200071；4.中鐵工程設計咨詢集團有限公司，北京100070；5.北京交通大學土木建筑工程學院，北京100044

軌道幾何不平順是輪軌系統的激擾源，是引起機車車輛產生振動和輪軌動作用力的主要原因。高速鐵路要求軌道必須具有高平順性［1］。軌道幾何不平順的檢測主要有動態、靜態兩種方式。對于檢測項目中的軌距、水平、三角坑指標，動態和靜態檢測的原理及計算方法一致。但對于高低、軌向，動態和靜態檢測的計算方法有明顯不同，動態檢測主要采用慣性基準法測量空間曲線，而靜態檢測主要采用弦測法。弦測法物理意義明確，簡單易懂，因此我國高速鐵路普遍采用綜合檢測車采集軌道不平順各檢測項目幅值，然后利用軌道幾何狀態測量儀、0級軌道檢查儀、弦線、道尺等靜態手段檢查復核，最后用靜態檢查結果擬定維修方案，以保證高速鐵路線路的高平順性。

我國常用的弦測法主要包括矢距差法與中點弦測法［2-4］。矢距差法來自德國經驗，用于控制高速鐵路的線形，存在與車體加速度匹配性較差、含有里程相位差、基礎變形時幅值過大等缺點，且現有固定30 m、300 m基長的5 m、150 m矢距校核的矢距差評價測量并不能有效控制影響行車安全性和舒適性的全頻段。而中點弦測法物理意義更為明確，可避免上述缺點。因此，多數國家鐵路線路運營維護時采用中點弦測法評價軌道幾何不平順。

本文以弦測原理為基礎，結合動力學模型，建立弦測值與車輛響應的關聯，提出弦測標準體系，以期更好地指導養護維修作業。

1 弦測法波長的選擇

1.1 弦測法測量原理

弦測法以固定弦長為測量基準，采用等間隔采樣，得到各個采樣點弦測值，數學計算模型為

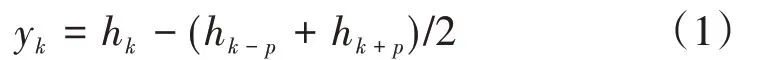
式中：k為采樣點里程，m；yk為里程k處弦測值；p為半弦長，m；hk、hk-p、hk+p分別為里程k、k-p、k+p處的軌道高程。

相應的傳遞函數H(ω)為

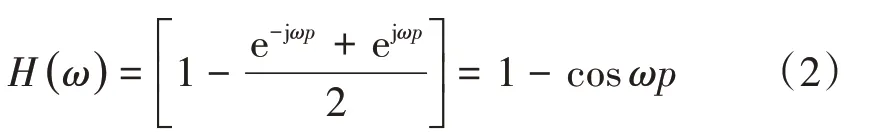
式中：ω為空間角頻率，rad·m-1，ω=2π/λ，λ為軌道不平順波長。

由式（2）可知，弦測法的傳遞函數隨著ω的變化在0～2區間變化。不同波長傳遞函數不同，導致部分波長段不平順幅值被放大，部分波長段不平順幅值被縮小，甚至在某些特征波長區段，傳遞函數為0，不平順幅值輸出結果為0。而不同弦長有效測量波長范圍不同，為確保檢測到需要的波長段，應當采用不同的檢測弦長。10 m弦和60 m弦中點弦測法的傳遞函數見圖1。

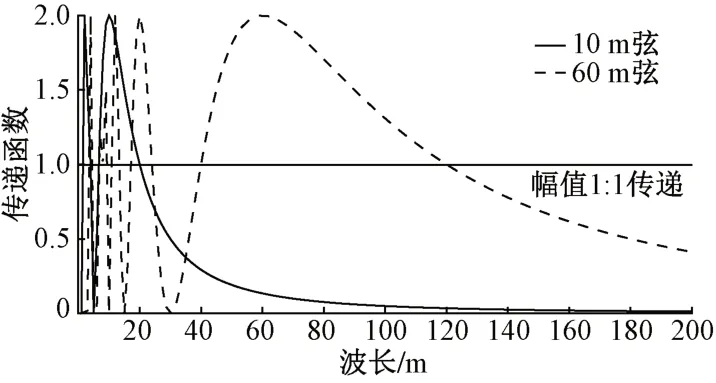
圖1 中點弦測法傳遞函數

1.2 波長的管理范圍

軌道不平順可視為由不同波長、不同幅值的正弦波疊加而成。不同波長的軌道不平順對列車運行安全性和乘坐舒適性的影響不同。其中，短波不平順（波長1 m以下）主要影響列車運行的高頻振動和噪聲；中波不平順（波長1～30 m）主要影響列車運行安全性和乘坐舒適性；長波不平順（波長30～120 m）主要影響乘坐舒適性；更長波長的不平順（波長120 m以上）對列車運行的影響較小，可以不予考慮。因此，為保證列車運行安全性和乘坐舒適性，應進行120 m及以下波長軌道不平順的檢測［5-6］。

1.3 弦長的有效測量范圍

采用中點弦測法時，最常用的測弦長度為10 m，有效測量波長為7～20 m。隨著列車速度的提高，影響乘坐舒適性的波長不斷增大，各國紛紛提出了更長弦長的測量方法。例如，日本增加40 m長弦，韓國增加30 m長弦，英國增加20 m長弦，美國增加20 m和40 m長弦。日本專家認為［7］，在相同的軌道狀態下，車輛振動隨列車速度的提高而增大，為了保證行車安全，在不延長弦長的情況下，建議提速到320 km/h時40 m弦長的維修管理值要適當減小。

由于影響高速列車乘坐舒適性的軌道不平順波長應控制到120 m，根據中點弦測原理，滿足有效測量的弦長應不小于60 m。為保證弦測結果與車體響應的相關性，測弦長度應不低于40 m。因此，弦測法長弦最大采用60 m。中點弦測法弦長和控制波長的關系見表1。

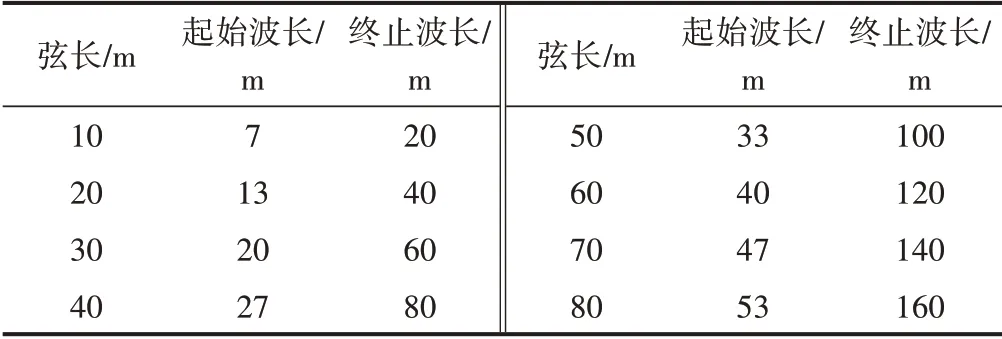
表1 不同弦長有效檢測波長范圍（傳遞函數≥1.0）

由表1可知，10 m弦和60 m弦中點弦測法并不能很好地檢測20～40 m波段不平順（按傳遞函數≥1.0計算），須對弦長控制標準進行補充。增加20 m弦中點弦測法，其有效測量波長范圍為13～40 m，結合已有的10 m弦和60 m弦中點弦測管理標準，就可以完全覆蓋影響車輛運行的所有波長軌道不平順。因此，采用10 m弦、20 m弦、60 m弦中點弦測法完全可以滿足200（不含）～350 km/h速度等級高速鐵路軌道靜態幾何不平順波長要求。

2 弦測法幅值管理值

2.1 10 m弦和60 m弦的幅值評判

10 m弦中點弦測法的控制標準主要通過動力學仿真、現場經驗和實車試驗得出。我國250（不含）～350 km/h速度等級靜態10 m弦幾何尺寸容許偏差管理值見表2［8-9］。其中限速為200 km/h。

表2 250（不含）～350 km·h-1線路軌道10 m弦靜態幾何尺寸容許偏差管理值 mm

60 m弦中點弦測法標準建議值可通過動力學仿真結合弦測值與車體加速度的關系統計分析得到［2］，幾何尺寸容許偏差管理值見表3。由于長波不平順主要影響行車舒適性，60 m弦管理值不考慮限速情況。

表3 250（不含）～350 km·h-1線路軌道60 m弦靜態幾何尺寸容許偏差管理值 mm

2.2 20 m弦的幅值評判

20 m弦有效測量波長為20～40 m，此波長區段軌道不平順同時影響列車運行的安全性和舒適性，因此須要建立動力學仿真模型，分析20 m弦測值與輪重減載率、脫軌系數及車體加速度的關系。

利用UM軟件建立CRH380B型動車組仿真模型（圖2）。車輛模型離散為1個車體、2個構架、8個軸箱和4個輪對，共計15個剛體。

圖2 CRH380B型動車組仿真模型

為減少人為構造不平順與實際不平順的差異，截取綜合檢測車實測數據作為軌道不平順輸入，幅值相同時，波長越小運行安全性越差，因此20～40 m波長區段中20 m波長最危險。此外，當軌道不平順波長為20 m時，采用20 m弦測傳遞函數為1.0。因此，選取20 m波長的周期性不平順區段。某一區段數據樣本及其功率譜密度如圖3所示。

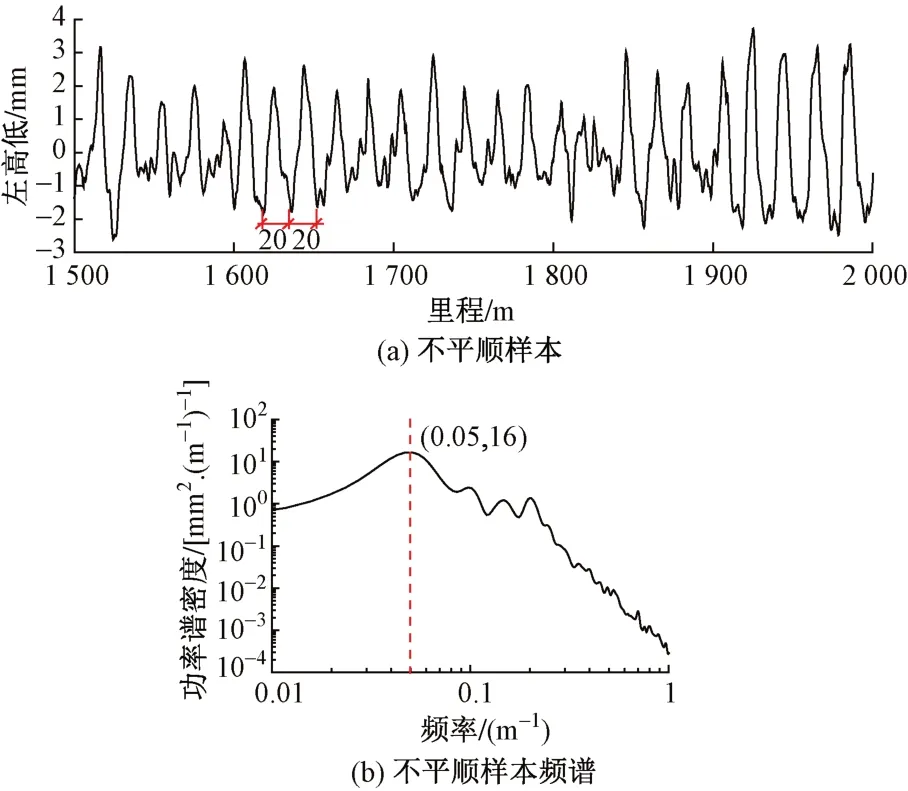
圖3 周期性不平順樣本示例

為了提高結果的可靠性，選擇10組高低不平順、10組軌向不平順共20組樣本進行計算，以計算結果的90%置信下限作為最終結果。動車組分別以300、350、400 km/h依次通過20組樣本線路，對軌道不平順中的左右高低、左右軌向分別乘以比例增大系數，模擬不平順幅值的演變發展情況。基于車輛運行安全性、舒適性的規范要求，以存在有周期性高低、軌向不平順的20個激勵作為基礎樣本，分析動車組以不同速度等級通過時不平順幅值與動力響應的關聯關系。

圖4為CRH380B型動車組以300 km/h通過某實測周期性高低不平順樣本時，輪重減載率與高低關聯性時程曲線。可以看出，輪重減載率峰值與高低不平順峰值出現位置幾乎完全一致，二者的關聯性非常好。仿真計算結果表明，隨著不平順幅值的增加，對于高低不平順，輪重減載率先達到了安全限值0.8，成為最重要的控制性指標；對于軌向不平順，脫軌系數率先達到了安全限值0.8，成為最重要的控制性指標。

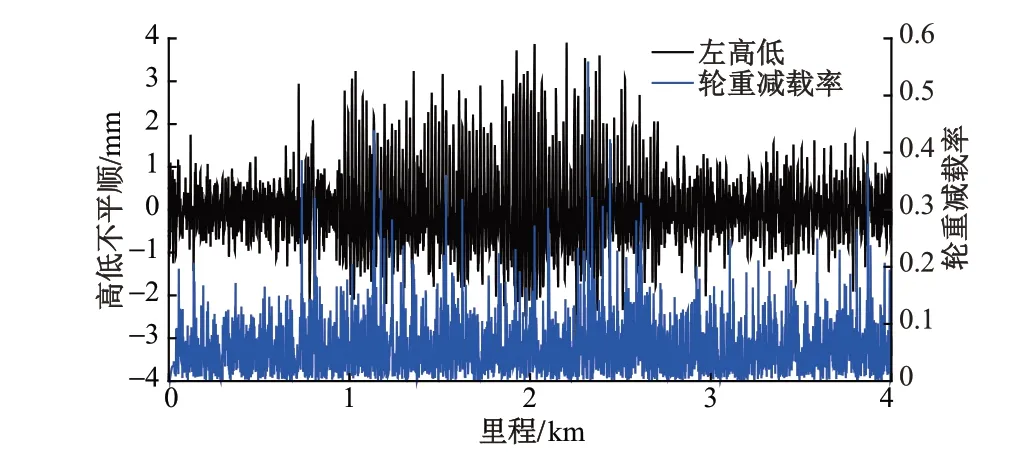
圖4 輪重減載率與軌道高低不平順關聯性時程曲線

2.2.1 高低不平順幅值

根據仿真計算結果，隨著高低不平順幅值的增加，輪重減載率先達到了安全限值0.8，車體垂向振動加速度最大值僅為0.55 m/s2，其他動力學指標處于更為安全的水平。輪重減載率到達0.8時，車速300、350、400 km/h對應的動態檢測及20 m弦靜態檢測（簡稱20 m弦測）的左右高低不平順峰值數據見圖5。

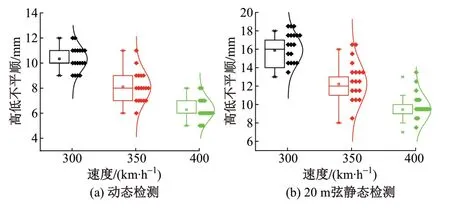
圖5 高低不平順峰值檢測數據

通過數理統計方法，對10個樣本的左高低、右高低峰值進行概率分布統計，結果見表4。

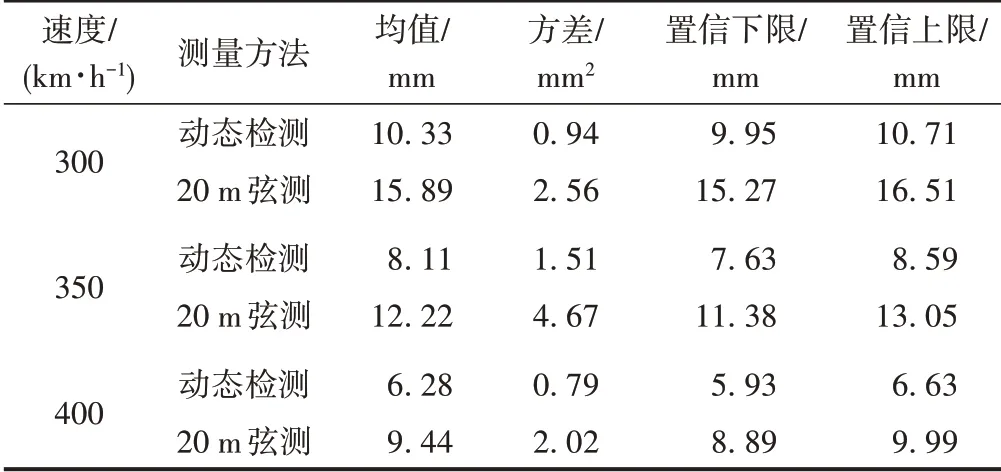
表4 10個高低不平順樣本峰值數據統計結果

考慮安全余量，統一選取置信區間下限作為垂向軌道不平順的管理限值，得到各行車速度等級所對應的高低不平順安全控制要求。在300～400 km/h速度區間內，20 m波長周期性高低不平順管理限值見表5。該限值滿足高置信度要求，而且具有普遍性。

表5 周期性高低不平順管理限值

2.2.2 軌向不平順幅值

根據數值模擬計算結果，隨著軌向不平順幅值的增加，脫軌系數率先達到了安全限值0.8，車體橫向振動加速度最大值為1.05 m/s2，其他動力學指標處于更低水平。脫軌系數到達0.8時，車速300、350、400 km/h對應的動態檢測及20 m弦測的左右軌向不平順峰值數據見圖6。

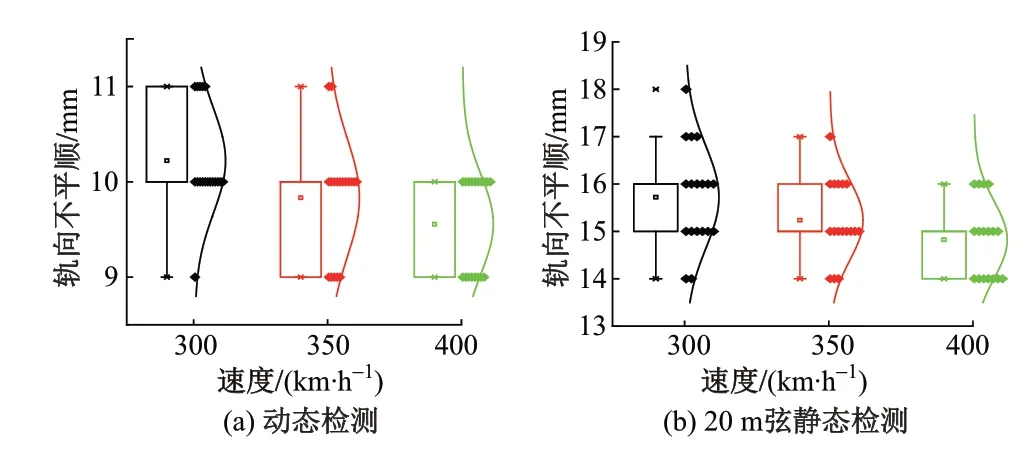
圖6 軌向不平順峰值檢測數據

通過數理統計方法，對10個樣本的左軌向、右軌向峰值進行概率分布統計，結果見表6。

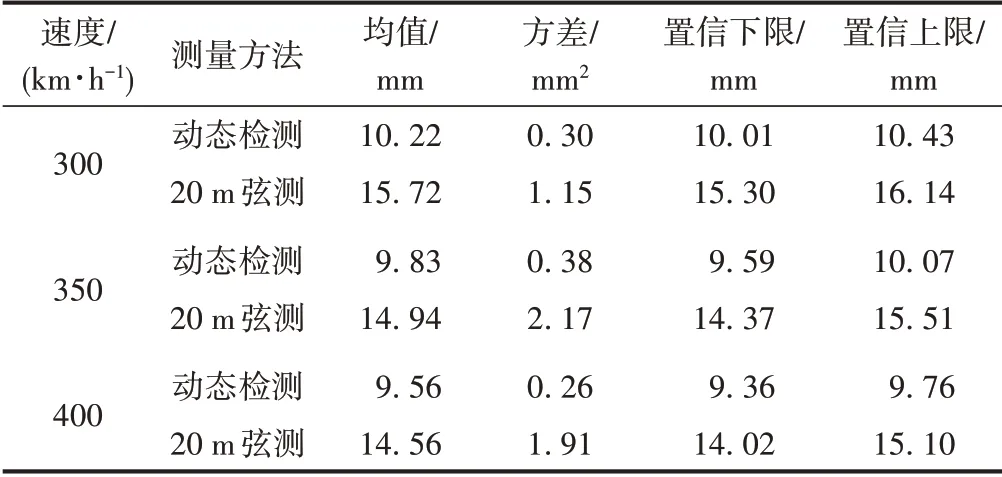
表6 10個軌向不平順樣本數據統計結果

考慮安全余量，統一選取置信區間下限作為橫向軌道不平順的管理限值，得到各行車速度等級所對應的軌向不平順安全控制要求。在300～400 km/h速度區間內，20 m波長周期性軌向不平順管理限值見表7。該限值滿足高置信度要求，且有普適性。

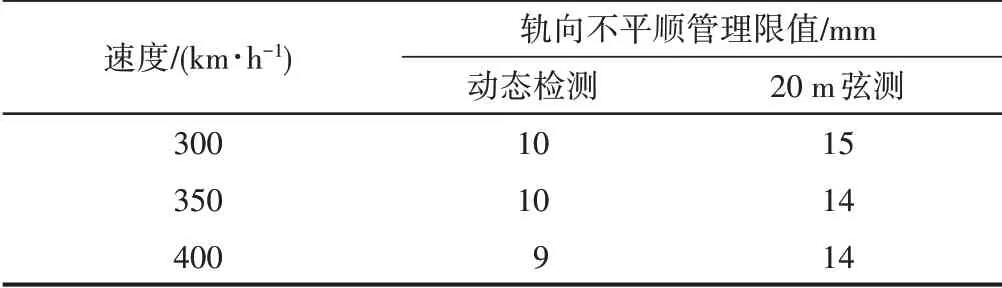
表7 周期性軌向不平順管理限值

對比表5和表7可知：運行速度為300 km/h時，高低不平順和軌向不平順管理限值差別很小；隨著運行速度的增加，高低不平順幅值變化比較顯著，從14 mm降到9 mm；軌向不平順受速度的影響較弱，在300～400 km/h速度區間內管理限值非常相近。

英國鐵路網（Network Rail）公司軌道幾何狀態標準中增加了20 m中點弦控制標準，并給出了警告值作為管理值標準［10］，見表8。美國《車輛軌道相互作用安全規則》［11］中規定高低和軌向不平順分別采用9.4 m弦、18.9 m弦、37.8 m弦來測量，給出了18.9 m的安全控制標準作為管理值。對于3波及以上連續不平順給出了更為嚴格的控制標準（安全值）［12］，見表9。此外，資料顯示，德國高低和軌向不平順20 m弦驗收標準為3 mm［13］。

表8 英國軌道不平順20 m弦中點弦測管理值

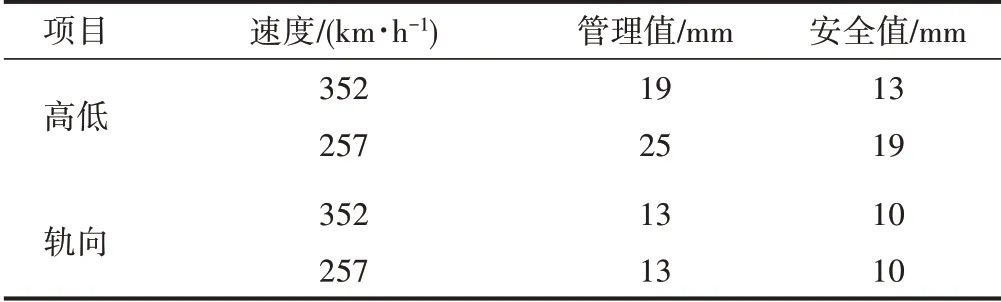
表9 美國軌道不平順18.9 m弦中點弦測管理值

結合動力學仿真結果，按照輪重減載率或脫軌系數0.4、0.6、0.8，劃分為計劃維修、臨時補修和限速（200 km/h）三擋。參考英國、美國和德國20 m弦管理值，結合我國現場經驗，再補充作業驗收管理值，最終提出20 m弦高低和軌向不平順的容許偏差管理值，見表10。

表10 250（不含）～350 km·h-1線路軌道20 m弦靜態幾何尺寸容許偏差管理值 mm

3 靜態弦測標準體系

3.1 弦測標準體系建立

根據上述研究成果，對于250（不含）～350 km/h速度等級的高速鐵路，為保證動車組運行安全和舒適性，須建立10 m弦、20 m弦、60 m弦中點弦測法評價管理體系。各弦長靜態弦測控制標準建議管理值見表11。

表11 250（不含）～350 km·h-1軌道靜態弦測容許偏差建議管理值

3.2 工程實例驗證

選取一設計速度為350 km/h的新建高速鐵路K85+000—K87+000區段，其靜態檢測和綜合檢測車檢測數據得出的高低標準差對比見圖7。其中高低標準差采用滑動步長10 m、區段200 m進行計算。

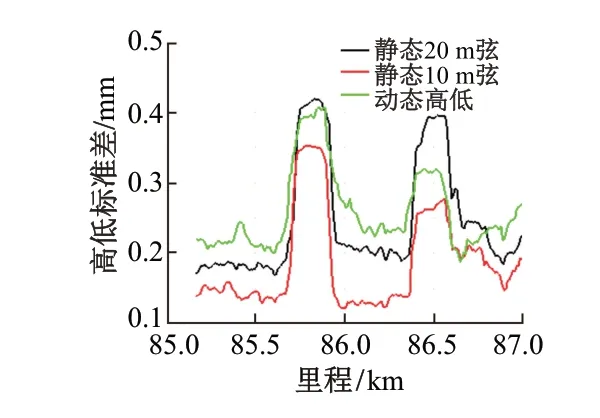
圖7 不同測量方法高低標準差對比

由圖7可知：①部分區段如K86+357—K86+599綜合檢測車標準差介于10 m弦和20 m弦高低標準差之間，說明本區段軌道不平順主要由較長波長成分組成，因此，為了滿足高速鐵路動態不平順要求，不僅需要10 m弦控制，還需要20 m弦控制。②對于平順性較好區段，如K85+169—K85+640，由于動車荷載作用，綜合檢測車標準差要大于靜態測量值。

選擇一設計速度為300 km/h的運營高速鐵路日常維修數據進行分析，某區段60 m弦靜態檢查結果見圖8。

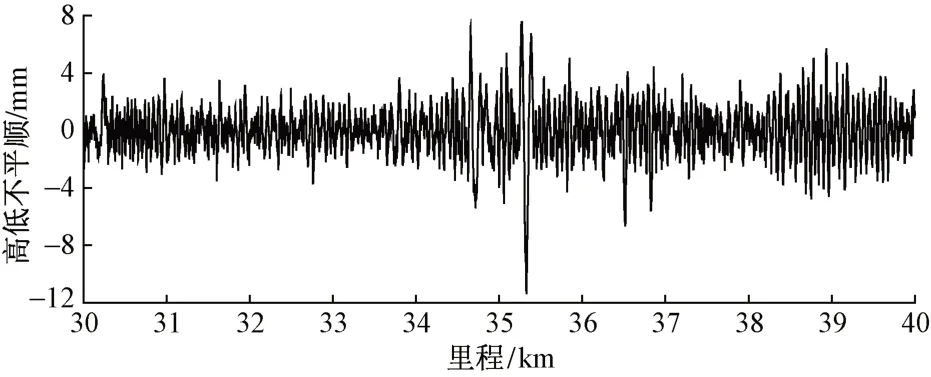
圖8 某線路區間60 m弦檢測高低不平順波形

由圖8可知，里程K35+320處60 m弦測值達到11.35 mm，超過維修標準。現場對該區段進行整修，整修后綜合檢測動車組長波不平順由幅值6.9 mm降為2.5 mm，垂向加速度由0.10g降為0.04g，改善效果較為明顯。

4 結論

為了完善軌道幾何不平順檢測中靜態弦測標準體系，本文以弦測原理為基礎，結合靜態弦測值與車輛響應的關聯關系，提出了新的靜態弦測標準體系。主要結論如下：

1）中點弦測法測量結果與車體加速度關聯性較好，與檢測位置無關，測量結果與實際結果不存在相位差。因此，采用中點弦測法可較好地評價軌道幾何狀態不平順。

2）根據影響列車運行的安全性和舒適性波長范圍以及中點弦測法不同弦長的傳遞函數，明確了對于高速鐵路，弦長應取10、20、60 m。

3）建立動車組仿真模型，從實際線路中選擇典型的周期性波長區段進行仿真計算，并參考國外管理值，建立了10 m弦、20 m弦、60 m弦軌道幾何不平順靜態弦測標準體系。

4）在某新建高速鐵路和運營高速鐵路區段試用的結果表明，該標準體系能夠準確地評價軌道幾何不平順，并將動靜態評價標準進行了關聯，可以更好地指導養護維修作業。