基于多柔體動力學理論的接觸網找形方法

邱江洋，梅桂明，王江文，羅 群

(西南交通大學牽引動力國家重點實驗室，成都 610031)

列車在高速運行時穩定的受流質量是高速列車設計的一個重要因素，而直接影響受流質量的就是受電弓與接觸網之間的接觸關系[1?2]。研究弓網系統之間的接觸關系則需要進行弓網系統的動力學建模[3]。

在進行動力學計算之前，動力學模型的初始條件及其重要，它直接影響著動力學模型的計算結果[4?5]。對于弓網系統也是一樣，接觸網的初始條件表征了接觸網系統在重力場、預張力和約束條件下的平衡構型。國內外眾多學者對接觸網系統的平衡構型進行了計算，利用懸鏈線方程[6?7]，將接觸網系統離散為懸鏈線單元，忽略結構的抗彎剛度，對接觸網的平衡構型進行計算；類似的采用拋物線單元[8]，對簡單鏈型懸掛接觸網進行離散，然后進行平衡構型的計算；意大利學者Bruni等[9]總結了全球10家致力于研究弓網關系的團隊針對一個標準的弓網模型進行的動力學計算，里面也包含了每個單位對于接觸網的找形方法。不難看出，從現有的接觸網建模技術來看[10?19]，針對接觸網找形問題，國內外學者都是針對接觸網的有限元模型，對其平衡狀態下的系統廣義坐標(或者還包括單元初始長度)進行計算，而計算精度大多都依賴于接觸網離散模型的自由度，這也是傳統有限單元基于小變形假設所帶來得一個不可避免的問題。

多柔體動力學理論在經過幾十年的發展后，在工程領域取得廣泛應用。其中由Shabana[20]提出的絕對節點坐標法(ANCF)，由于系統的廣義坐標直接采用節點的絕對位置矢量和絕對梯度矢量，由于將節點廣義坐標中的梯度矢量替換了傳統有限單元的小轉動矢量，所以沒有轉動幅度的限制，因此在描述鐵路接觸網系統、電梯升降繩以及流體建模等[19,21?23]眾多柔性大變形問題具有很多優勢。而基于連續介質力學[20]的ANCF在描述其有限單元時，其單元的二階連續性能夠使系統有限元模型的維度大大降低，因此能更好地進行有限元模型的動力學計算。

本文采用基于ANCF描述的多柔體動力學理論建立接觸網的有限元模型，接觸網由兩節點的ANCF索單元進行離散，模型考慮了接觸網中的彎曲變形和軸向變形，考慮到接觸網中幾乎不存在扭轉變形，所以忽略了接觸網中的扭轉變形。由于接觸網系統是一種張緊的工程結構，在找形分析中使單元的初始長度變化來滿足接觸網中的張力要求。并根據拉式方程推導了在索單元長度未知情況下的動力學模型，針對平衡構型的計算問題，對動力學模型進行退化處理。在引入未知單元長度的模型后，需要根據接觸網中的張力條件進行補充方程，得到的接觸網平衡構型的計算模型整體計算維度非常小，僅與每跨中的吊弦數量相關。最后通過3個數值算例，分別從單元穩態構型的計算、簡單接觸網穩態構型的計算以及工程應用中的接觸網穩態構型的計算上驗證了本文找形方法的可行性。

1 ANCF基本動力學理論

1.1 單元長度未知的ANCF索單元理論

兩節點的ANCF索單元如圖1所示，其中心線上任意點P的絕對位置矢量可表示為：

圖1 兩節點索單元變形前后示意圖Fig.1 Deformed and un-deformed two-nodes cable element

式中：L為單元初始長度；l為任意點P在中心線上的弧長坐標，滿足：

單元初始長度L為時變的未知量，定義單元初始長度L為：

單元的動能可表示為[24]：

單元勢能由應變能和重力勢能組成：

1.2 索單元動力學方程

在引入約束條件下，由帶約束乘子的第一類拉格朗日方程建立索單元動力學方程：

由式(15)可推導得變長度索動力學模型的另一種表達形式：

1.3 動力學方程求解方法

式(16)是一組典型的微分-代數方程(DAEs)，本文采用經典的增廣法[26]進行求解，為了使解趨于穩定，引入閉環系統：

對于多單元系統，采用傳統有限元共用節點組裝的方法，根據式(20)，即可求出系統的廣義坐標q、廣義速度q˙和廣義加速度q¨。

2 動力學模型退化的找形方法

2.1 平衡狀態下的動力學模型

第1節推導了單元長度未知情況下的索單元動力學模型，而平衡狀態就是動力學模型中一個特殊情況。對應的條件是與時間相關的一階、二階導數均為0，即：

而式(23)在找形問題中需要求解的變量只有單元的廣義坐標，所以可以根據式(23)得到：

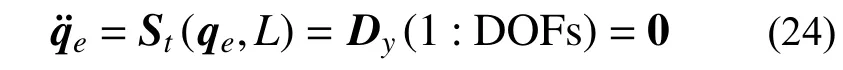
式中：DOFs為單元自由度，對于本模型的ANCF索單元，單元自由度為12；另外定義：

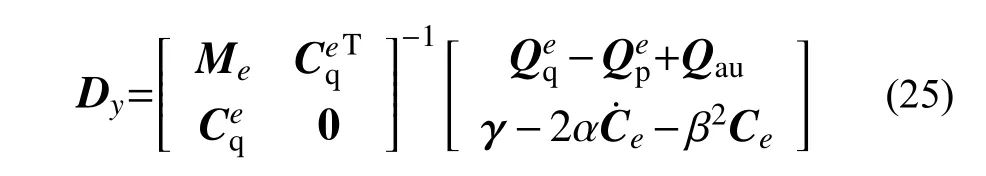
值得注意的是，在式(25)中，未知的只有由動能附加項引起的廣義力附加項，動能附加項表達式為：

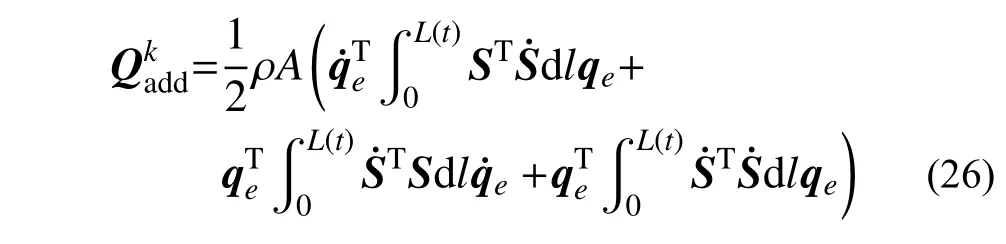
而在應用拉式方程建立索單元動力學模型時，動能附加項參與計算時，會引起兩項廣義力附加項：

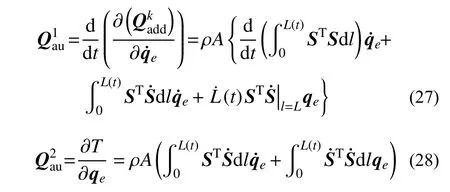
但當單元處于平衡狀態時，由于式(28)和式(29)中均含有與時間相關的導數項，根據式(22)可知：

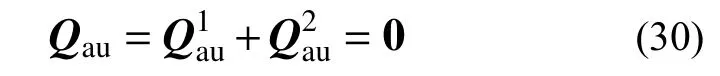
由此可知，由動能附加項引起的廣義力附加項：

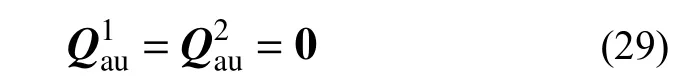
所以，式(25)可改寫為：

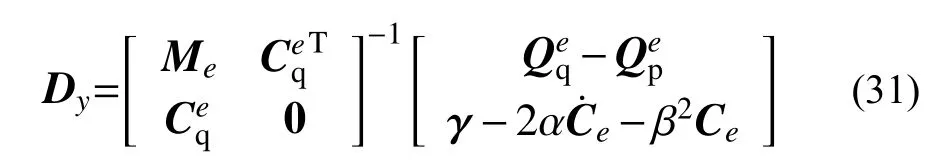
2.2 引入張力條件的找形方法

根據式(24)可知，由動力學模型退化得到一組獨立的非線性方程組的維度只是單元自由度數，但還需要求解的還有單元初始長度，所以需要再添加一個獨立的方程，對于張緊的單元，可根據張力條件補充方程：

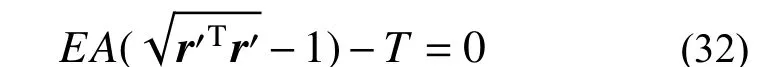
式中，T為給定的張力條件。聯立式(24)和式(32)可得到一組非線性方程組：

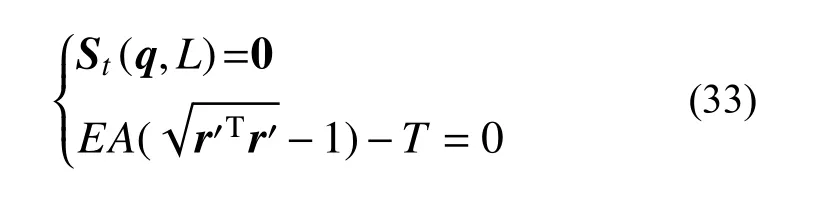
3 接觸網找形問題

3.1 接觸網有限元模型

簡單鏈型懸掛接觸網如圖2所示，以3跨簡單鏈型懸掛接觸網為例，吊弦作為連接承力索和接觸線的結構，使得接觸網成為一個彈性均勻分布的系統，同時，定位裝置將接觸線和承力索并不是沿軌道呈直線分布，而是呈“之”形分布，如圖2中俯視圖所示，從而使受電弓滑板能夠均勻磨耗。另外，接觸線和承力索的下錨處安裝了棘輪補償裝置，使得接觸線和承力索一直處于張緊狀態，在圖中用Tcw、Tmw表示。

兩個吊弦之間的接觸線/承力索、接觸線/承力索與定位裝置之間，還有定位器均采用一個變長度索單元。接觸網系統離散為N個變長度ANCF索單元：

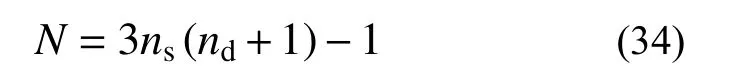
式中：ns為跨數；nd為一跨內的吊弦數量。

3.2 接觸網中的約束處理

為了簡化接觸網中的約束，在接觸網有限元模型中的連接方式均采用球鉸約束[19]，在絕對坐標系下的3單元球鉸連接如圖3所示。其數學模型表示為：{

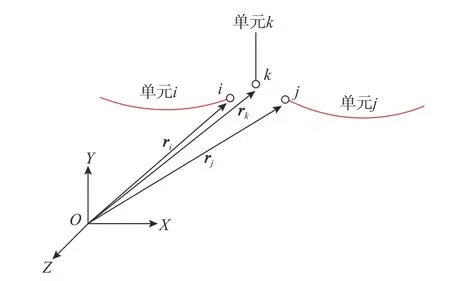
圖3 3個單元球鉸連接示意圖Fig.3 Schematic diagram of spherical hinge connection of 3 elements

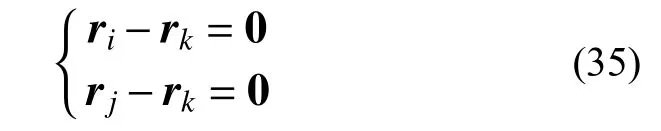
在接觸網中，吊弦與接觸線單元、吊弦與承力索單元均采用這種約束。

另外，接觸網系統的邊界條件也可簡化為接觸網系統的邊界單元鉸接在固定點：

式中：rb表示邊界處的位置矢量，即包含承力索和接觸線的兩端點的位置矢量；rfix表示邊界點約束的位置矢量。

3.3 接觸網的平衡構型

接觸網的找形問題就是確定接觸網有限元模型在平衡狀態下系統的廣義坐標，由于接觸網采用變長度索單元進行有限元劃分，平衡構型還需要確定的是單元的初始長度，用x表示為平衡構型：

針對接觸網的找形問題，不僅只是確定接觸網系統在邊界條件下的平衡構型，吊弦還有預分配的約束條件：

式中：rd為吊弦下端的位置矢量；rdesign為吊弦下端點的預設條件。

3.4 接觸網找形應用

根據吊弦預配要求，那么接觸線就可從接觸網系統中分離出來單獨求解，再根據接觸網的離散方式，那么每個接觸線單元就可處理為兩端鉸接在已知點的張緊懸鏈線模型

3.4.1接觸線找形分析

將接觸線的每個單元處理為兩端懸掛在已知點的懸鏈線模型，而對于接觸網中的張力主要分量是水平分量，所以這里簡化處理為：

式中：Tcw為接觸線的張力條件：上標“x”為張力的水平分量。

利用水平張力作為張力補充條件，那么應用式(33)對每個接觸線單元進行找形分析時，則需要改寫為：

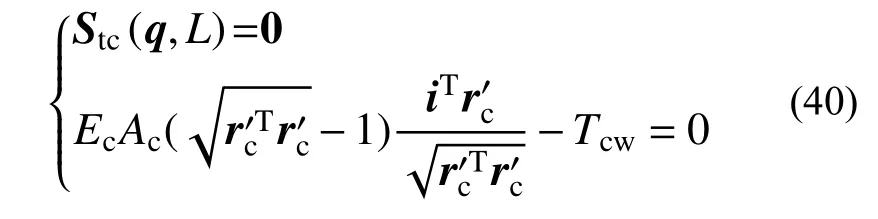
式中，Ec、Ac分別為接觸線的彈性模量和截面積。

完成接觸線的平衡構型求解之后，根據相應接觸線單元的穩態構型，提取在定位點處的合力作為定位器單元的張力補充條件，可以得到定位器穩態構型的求解方程：

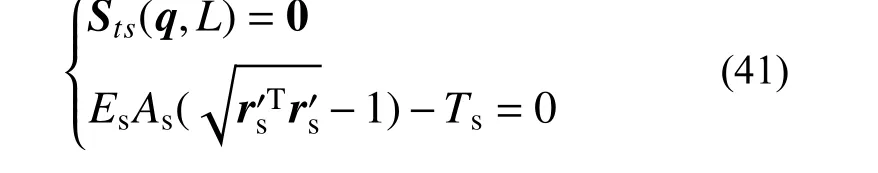
式中：i=[0,1,0]T；EcAc分別為定位器的彈性模量和截面積；Ts為反求得到的定位器所受張力。

3.4.2吊弦承力索系統的找形應用

在確定了接觸線的平衡構型后，與定位器類似的，每根吊弦單元的下端張力也可由相應的接觸線單元的平衡構型條件反求出：

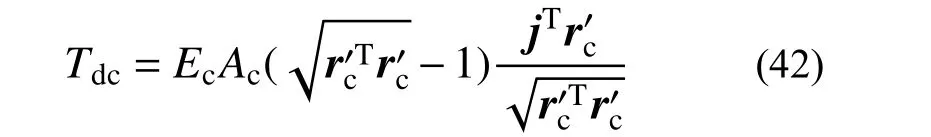
式中，j=[0,1,0]T，補充了吊弦的張力方程，對于承力索，張力補充方程與接觸線的張力處理方式一致：式中：Tmw為承力索的張力條件；上標“x”表示承力索張力的水平分量。

則對于承力索與吊弦組成的系統，其動力學方程由經典的有限元填裝方法可得到，相應的，對于由多單元組成的承力索吊弦系統，需要補充相應單元數的張力條件。利用式(42)可補充吊弦單元的張力條件，再由承力索的水平張力條件，那么可以得到吊弦承力索系統的平衡構型求解方程：

式中：n=nd+1；Em、Am、Ed、Ad分別為承力索和吊弦的彈性模量和截面積。張力補充方程的前n=nd+1個方程由各個承力索單元提供，而最后nd個方程由吊弦補充方程提供；對應了每個單元的補充方程。

3.4.3小結

總結前兩部分的找形應用過程，可以看出本文的方法是基于分模法[27]的思路，先將接觸網進行分模處理，將接觸線的平衡構型求出后，利用其平衡構型求出相應吊弦點處的吊弦力，以此補充相應缺失的張力控制方程，最后完成整個接觸網的找形分析；整個流程如圖4所示。

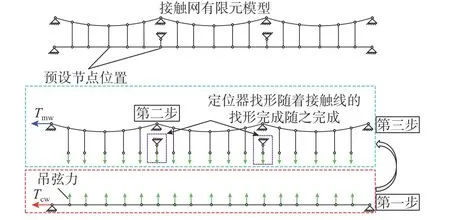
圖4 接觸網找形流程示意圖Fig.4 Schematic diagram of form-finding steps of the railway catenary

4 算例驗證

本節用3個算例對本文提出的找形方法進行驗證，包括懸鏈線模型、兩吊弦簡單接觸網模型和EN50318中的簡單鏈型懸掛接觸網模型。本文在針對接觸網進行找形分析時，針對接觸線的找形時是將每個接觸線單元視作一個懸鏈線模型(包含等高與不等高懸鏈線模型)，所以引入了懸鏈線模型進行初步驗證本文提出方法的可行性。

4.1 懸鏈線模型

懸鏈線示意圖如圖5所示，兩端鉸接在固定點處，同時端部還滿足張力控制要求。懸鏈線的密度為ρ=7800 kg/m3，截面直徑D=0.01 m，彈性模量為E=2.01 GPa，端部張力控制為T=15 kN。

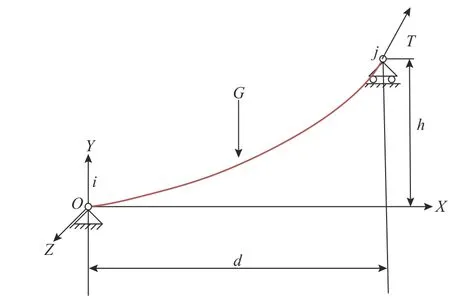
圖5 懸鏈線示意圖Fig.5 Schematic diagram of catenary

對該模型進行找形分析，跨距d=20 m，懸掛高度差分別取h=0 m、0.1 m、0.2 m、0.3 m、0.4 m、0.5 m。找形結果如下圖6所示。

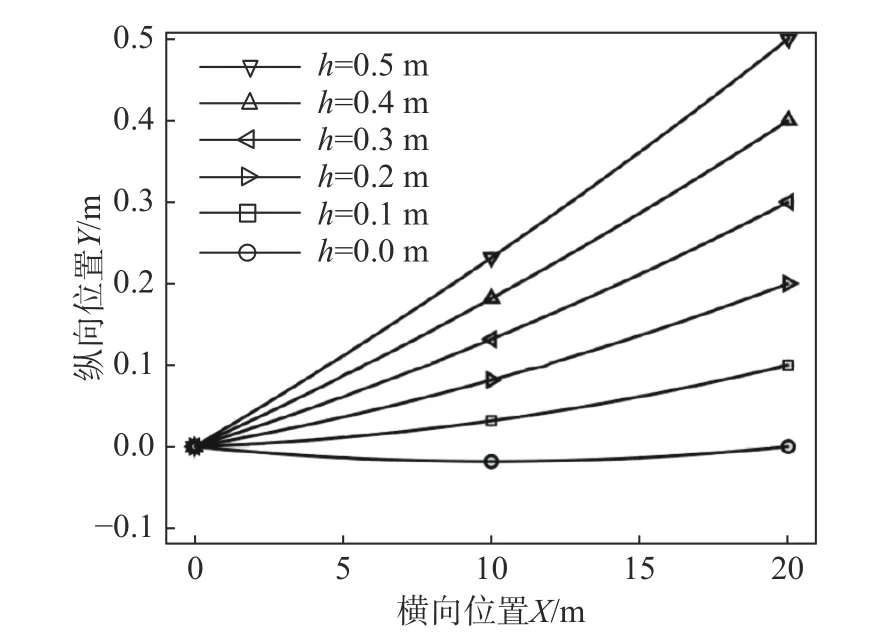
圖6 不同懸掛高度的懸鏈線找形結果Fig.6 Form-finding resultsof catenary at different suspension height

隨著懸掛高度的增大，懸鏈線穩態構型的最大靜撓度逐漸變小，穩態懸鏈線構型也逐漸逼近其對應懸掛點之間的連線。通過提取施加張力段的豎直張力分量分別為54.88 N、129.88 N、204.87 N、279.85 N、354.81 N、429.75 N，而張力的主要分力是水平分量，所以在端部或者懸鏈線中任意點偏置水平位置角度是逐漸增大的。

為了驗證找形結果的正確性，建立相應的動力學模型，再代入找形結果進行動力學仿真，不進行重復性的工作，只做圖6中高度為h=0 m,0.3 m的驗證，提取端部張力控制時程曲線如圖7所示。由張力的時程曲線可以看出，在使用本文中的方法進行找形的結果在代入到動力學模型中時，懸鏈線的端部張力的幾乎是不變的，盡管圖7(b)不等高懸鏈線的端部張力最后的穩態值與目標張力在數值上有一點差異(20 N)，但是其相對誤差僅為0.13%，這完全可以認為模型是穩定的。

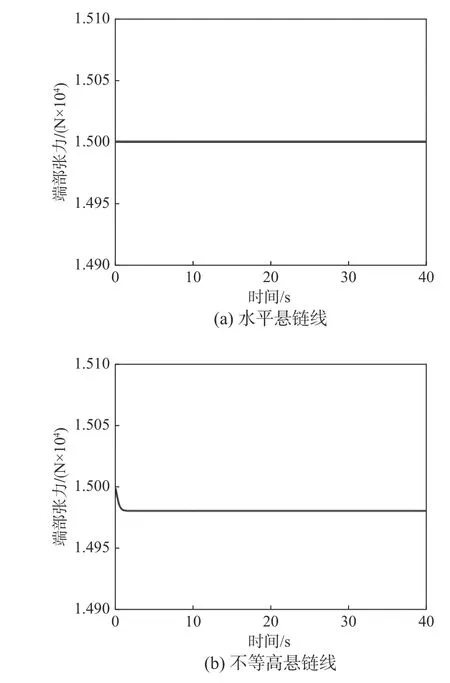
圖7 懸鏈線端部張力時程曲線Fig.7 Time history of tension at the tip of catenary

4.2 兩吊弦簡單接觸網模型

文獻[28]提出的兩吊弦單跨簡單接觸網如圖8所示，用于驗證弓網接觸的動力學響應。材料參數由表1給出，幾何參數由表2給出。作為一個經典的標準模型(benchmark catenary)，文獻[6,29]也對該模型進行了找形分析，也不乏基于絕對節點坐標法的找形方法[29]。

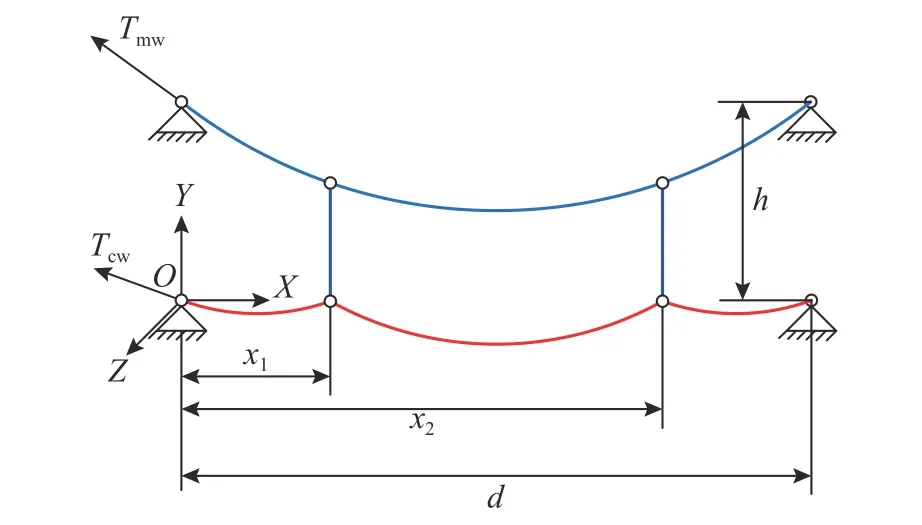
圖8 兩吊弦接觸網示意圖Fig.8 Schematic diagram of two dropperscatenary

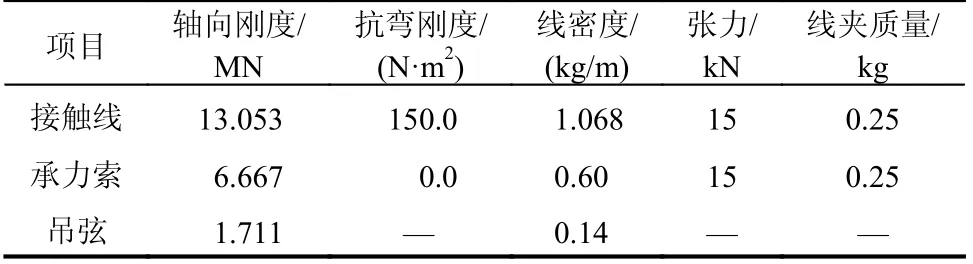
表1接觸網材料參數Table 1 Material parameters for the benchmark catenary

應用動力學退化方法進行找形分析，得到接觸網的穩態構型如圖9所示。

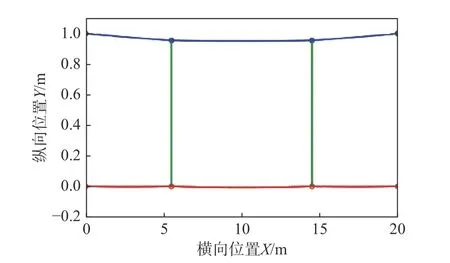
圖9 兩吊弦接觸網找形結果Fig.9 Form-finding result of the benchmark catenary

提取吊弦點處的吊弦力均為75.69 N，吊弦長度均為0.9552 m；從仿真結果也體現出了結構的對稱性；另外對于吊弦長度的計算結果來看，與文獻中給出的計算結果分別為：0.9579 m[6]、0.95 m[28]及0.9540 m[29]非常接近，相對誤差分別為0.55%、0.13%、0.28%。而在文獻[6]的模型中，接觸網的穩態構型是通過懸鏈線方程推導得到的解析形式，并沒有考慮接觸網的彎曲和軸向變形，但其他兩個模型以及本文中的模型均是將接觸網離散為有限單元模型，同時考慮了單元的軸向剛度和抗彎剛度，這說明針對該模型的軸向和彎曲變形在找形分析中是可以忽略的。另外值得注意的是，本文中接觸網的有限元模型僅采用8個ANCF索單元，但應用本文的找形方法得到的結果精度卻沒有降低，這是由于ANCF單元的插值函數是基于三次多項式插值推導得到的，具有二階連續性。

表2接觸網幾何參數Table 2 Geometrical parameters for the benchmark catenary

同樣的，將求解到的平衡構型代入到相應的動力學模型中進行驗證，提取控制端張力時程曲線如下：

由端部張力時程曲線圖10(a)接觸線端部和圖10(b)承力索端部，可以看出，由本文提出的找形方法得到的平衡構型代入到動力學模型中，動力學模型幾乎是不震蕩的，端部的張力的穩態值與設計張力的相對誤差分別為：接觸線0.0023%，承力索0.067%。可以看出，對于該模型，本文提出的找形方法能夠精確的求解到其平衡構型。

圖10 接觸網端部張力時程曲線Fig.10 Time history of tension of the benchmark catenary

4.3 鐵路接觸網系統

在工程應用上，本文采用歐洲標準EN50318[30]中的簡單鏈型懸掛接觸網為例，分別進行單跨和多跨接觸網找形分析。單跨接觸網如圖11所示。

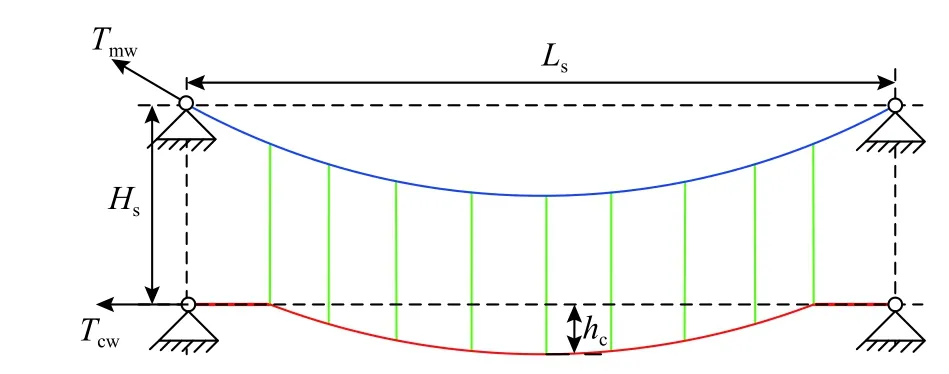
圖11 簡單鏈型懸掛接觸網示意圖Fig.11 Schematic diagram of a samplecatenary in EN50318

這個模型也在文獻[9]中作為一個標準模型進行研究，有全球10個致力于弓網研究的團隊針對本模型進行找形分析和弓網動力學性能評估。這種簡單鏈型懸掛結構應用在法國的LN2和意大利的C270接觸網系統中。接觸網的材料參數如表3所示，幾何參數如表4所示；另外由于存在吊弦的預分配條件，吊弦的預分配位置如表5所示。

表5 吊弦預配參數Table 5 Pre-allocated parametersfor droppers

應用本文的動力學方程退化方法進行找形分析，得到單跨接觸網的平衡構型如圖12所示。

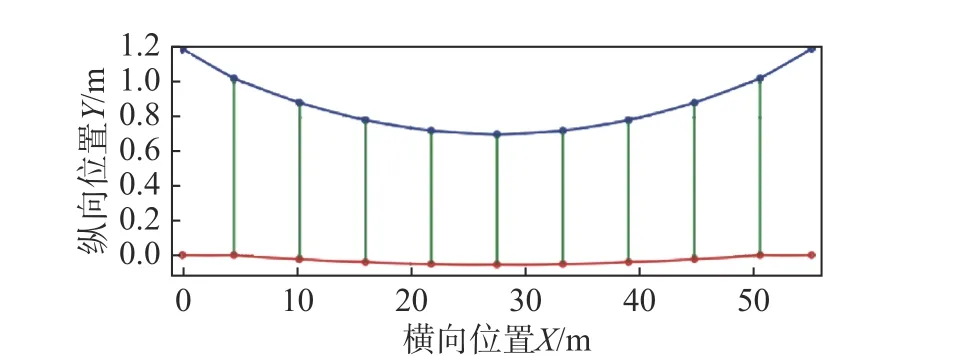
圖12 簡單鏈型懸掛接觸網平衡構型Fig.12 Equilibrium configuration of thesample catenary

10家單位都做過該模型的找形研究，由于方法的不同和模型約束考慮的不同，每家單位得到的結果都有差異，但大體上近似[9]。這里采用西班牙的一家單位PACDIN[19]的結果進行對比，提取接觸線的平衡構型對比如圖13所示。

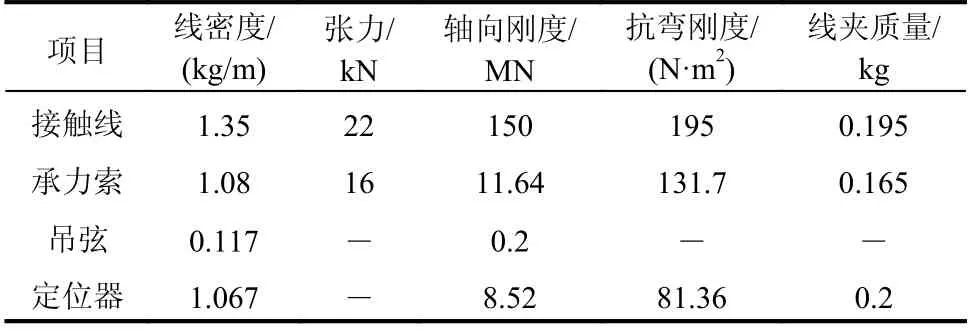
表3接觸網材料參數Table 3 Material parameters for the EN50318 catenary

表4接觸網幾何參數Table 4 Geometrical parametersfor the EN50318 catenary

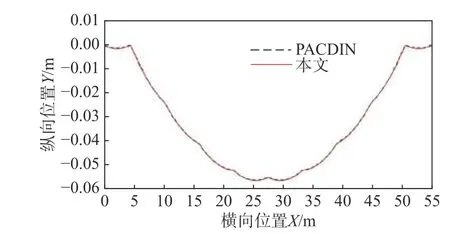
圖13 接觸線平衡構型的對比結果Fig.13 Comparison of equilibrium configuration of contact wire

吊弦是接觸網的重要部件，對于吊弦長度和吊弦力的計算，也與參考文獻進行對比，如表6所示。

從表6可以看出，在量化之后的找形結果對比中，對于吊弦長度的計算，兩種方法得到的結果相對誤差不大于1%，雖然吊弦力的計算上相對

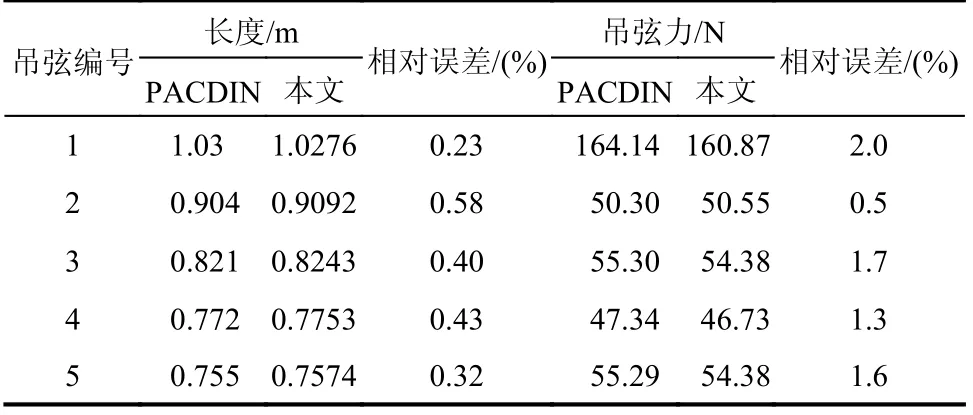
表6 吊弦長度與吊弦力計算結果對比Table 6 Comparison of the dropper's length and force by different methods

誤差較大，但也沒有超過2%。這也說明了本文找形方法的正確性，但本文中接觸網有限元模型的自由度卻非常小，相比于文獻[9]中10家單位的接觸網模型的自由度具有極大的優勢。

除此之外，從動力學的角度進行驗證，將得到的平衡構型代入到動力學模型中，驗證模型是否震蕩，提取得到的接觸線和承力索的端部張力如圖14所示。

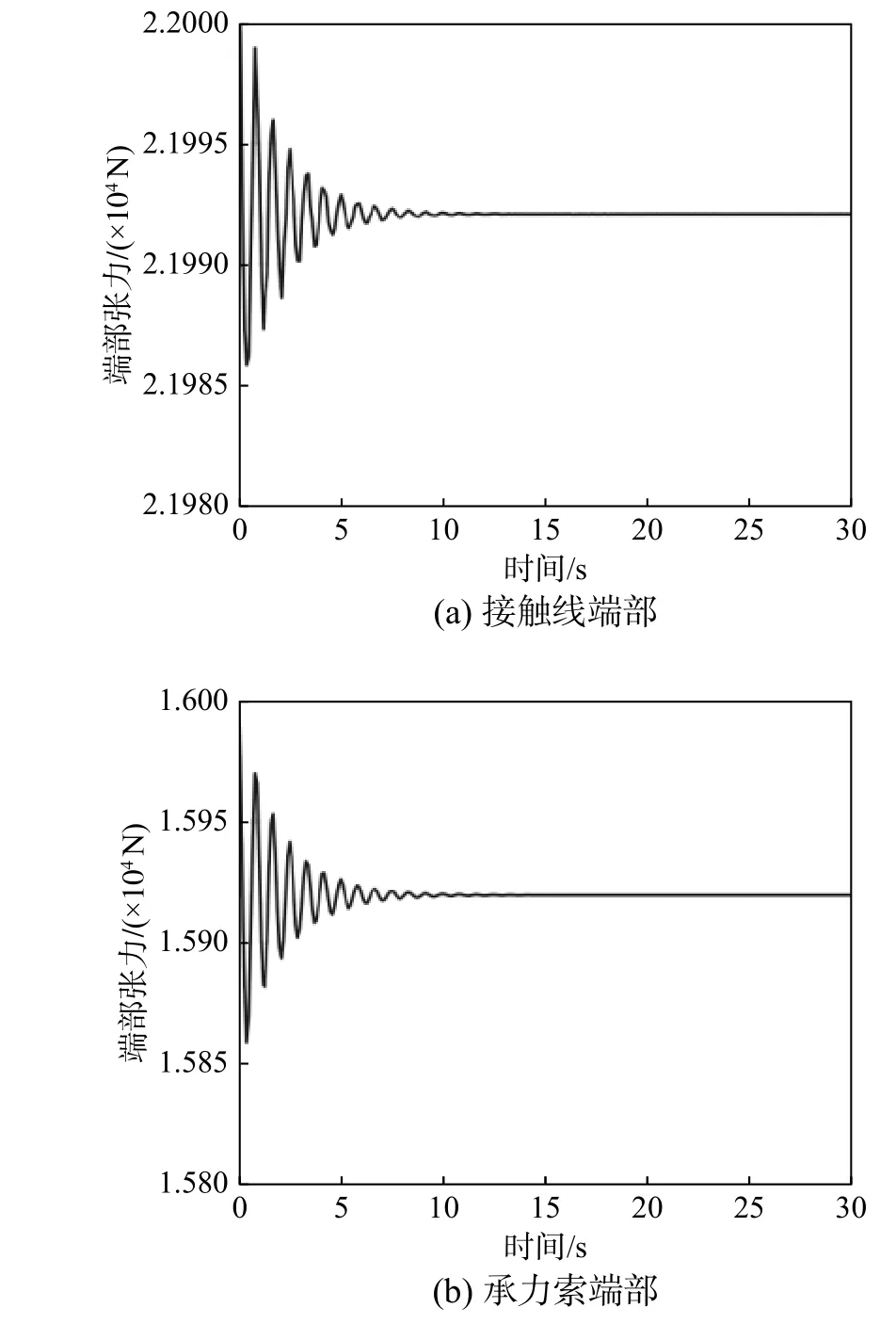
圖14 簡單鏈型懸掛接觸網端部張力時程曲線Fig.14 Time history of tension at thesample catenary’s tips

通過提取接觸線張力時程圖14(a)和承力索端部張力時程圖14(b)曲線可以看出，動力學模型在該初始條件下是基本處于穩態的，雖然一開始會有輕微的震蕩，但是可以看出張力的振幅并不是很大(20 N左右)，并且最終趨于穩定，穩定的端部張力數值與控制張力的相對誤差均小于1%。通過驗證動力學模型是否震蕩，更加直接地證明了平衡構型的正確性，進一步證明了本文提出的找形方法的可行性。

最后，對于該模型，進行多跨建模，需要考慮定位器的影響，得到找形結果如圖15所示。

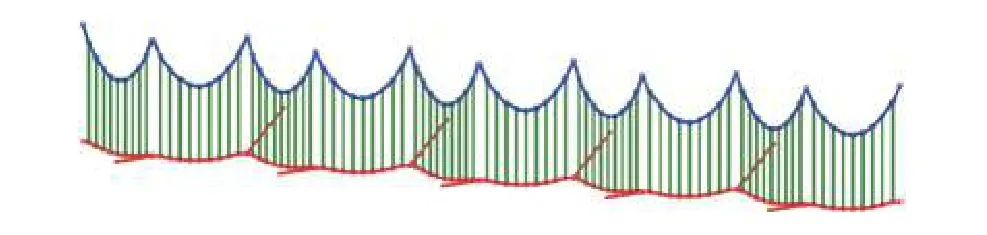
圖15 10跨簡單鏈型懸掛接觸網平衡構型Fig.15 Equilibrium configuration of the sample catenary with ten spans

同樣的，建立多跨接觸網動力學模型，將找形結果代入動力學模型中作為仿真初始條件，提取接觸線和承力索的端部張力時程曲線如圖16所示。

與單跨接觸網的驗證結果一致，根據接觸線張力時程圖16(a)和承力索的端部張力時程圖16(b)曲線可以說明系統是基本處于穩定的，開始震蕩的賦值相比也設計張力來說非常小,最后收斂的張力數值與設計張力的相對誤差不超過1%。

5 結論

本文提出了一種基于動力學退化模型的接觸網找形方法，根據平衡條件將未知單元長度的索單元動力學模型退化，再補充求解單元的初始長度的張力控制方程，推導了張緊索單元的找形方程。基于分模法的思想，將接觸線的平衡構型預先求出，進而得到吊弦單元的張力補充方程，再根據有限元填裝技術，推導了承力索吊弦系統平衡構型的計算方程，最后根據三個算例驗證，可以得到以下結論：

(1)基于ANCF理論和未知單元初始長度條件，根據平衡條件對動力學模型進行退化處理，推導了張緊單元的靜態構型的計算模型；該模型適用于長大張緊結構的靜態構型的計算，如鐵路接觸網，輸電線等。

(2)應用該模型進行EN50318中的簡單鏈型懸掛接觸網的找形分析，對比Benchmark中的某單位的計算結果，得到的接觸線的靜態構型幾乎一致，并且在吊弦長度的計算上，相對誤差均小于1%，吊弦力的計算上，相對誤差小于2%。滿足工程應用的要求。并且通過動力學模型的驗證，得到的張力控制的相對誤差小于1‰，驗證了本文方法的準確性。

(3)由于模型中能夠考慮穩態構型下的吊弦預分配條件，所以該模型適用于所有簡單鏈型懸掛接觸網的找形計算，能夠指導接觸網的設計和施工。

(4)由于該找形方法是基于動力學模型推導得到的，所以找形結果可應用于接觸網系統的動力學計算，動力學模型能夠快速地趨于穩定。