基于LV的SD模型反饋關系判定

汪 勇 徐 韜 龐天澤

(上海市城市建設設計研究總院(集團)有限公司1) 上海 2001254) (重慶市市政設計研究院2) 重慶 400020) (西安建筑科技大學土木工程學院3) 西安 710055)

0 引 言

系統動力學(SD)方法是一種以系統內部信息反饋控制理論為基礎，結合系統論、反饋控制論及決策論的系統仿真方法，它強調系統的行為模式主要取決于其內部的動態結構和反饋機制，通過變量間的反饋關系建立量化模型，利用計算機仿真模擬預測結果[1-2].

SD模型在構造過程中存在反饋關系不明顯或處于動態變化的狀態的反饋環，此時就無法直接構造反饋回路.需要將這些變量的反饋關系通過多種手段做出合理的量化.Peter[3]提出了系統動態反饋復雜性(system dynamic feedback complexity)的概念；Wolstenholme等[4-5]通過定義正負兩對的反饋環來構造雙循環基模，得出的模型更具有普遍性；國賈仁安等[6-7]提出了動態反饋復雜性層次分析的概念，利用流率基本入樹建模法、枝向量矩陣反饋環計算方法、基模生成集法對反饋基模進行了深入了研究，創建了更貼合實際的系統運行全部反饋環分析法.這一系列方法為我國SD模型的研究提供了規范化的框架.

本文在上述研究的基礎上，提出一種基于Lotka-Volterra判定理論(LV理論)的系統動力學(SD)模型反饋環節點研究的方法.LV理論是生態學中用以研究物種變化關系的重要理論，它的最大特點在于具有時變性質，能將不斷變化的變量關系量化[8-9]，這為SD模型中動態反饋關系研究提供了思路.文中通過經濟-人口-運輸的系統背景，闡述運輸子系統下運輸方式關系變化對GDP的影響.

1 LV理論改進SD模型

1.1 經濟-人口-運輸系統關系

經濟-人口-運輸系統中存在多個反饋循環，可通過人口與運輸兩個子系統來預測經濟水平子系統.人口子系統中研究的成果比較豐富，相關數據便于查詢，但運輸子系統是一個動態非線性的復雜系統，不僅受影響的因素多，而且系統內部各變量也在相互影響.以系統動力學的視角剖析整個經濟-人口-運輸系統，通過LV理論判定運輸系統變量之間的動態變化節點，對LV判定環中關系不明確的反饋暫時用虛線標注.構建SD模型下的經濟-人口-運輸系統關系圖，見圖1.

圖1 經濟-人口-運輸系統關系圖

運輸系統關系圖中大致分為三個循環：①經濟水平→人口數量→運輸需求→運輸價格→運輸收益，此循環為負反饋；②經濟水平→人口數量→運輸需求→運輸投資→運輸運量→運輸供給→運輸收益，此循環為正反饋；③運輸方式A→運輸方式B→運輸方式C，此循環無法直接判斷，運輸投資的增加會增大總體的運量，但該循環中各變量(即各種運輸方式)間存在相互影響的關系，可表現為促進、競爭、單向影響或無關聯的Logistic發展模式，即子系統中的單體變量的發展情況則需要通過LV理論分析界定.

經濟水平直接促進運輸需求的增長，同時運輸需求增長可通過增加運輸價格或增加運輸投資兩種方式實現，但由前面分析看出循環①是個負反饋過程，從系統角度來看，循環②增加運輸投資才是促進經濟發展長久之計.在循環②中存在更子一級別的循環③，循環③中各變量(即各種運輸方式)的關系相互影響，并處于動態變化當中，為研究循環②下的運輸經濟效益，需對循環③中變量關系進行LV判定，建立時變情況下的LV-SD模型.

1.2 構造LV-SD系統

將反饋圖中經濟、人口、運輸三個子系統作為整個系統的邊界條件.運輸子系統中存在運輸方式關系模糊的反饋環，為建立完整的系統動力學方程，需對該反饋環進行LV判定，求得相應的作用系數f，構造Lotka Volterra-System Dynamic模型(簡稱：LV-SD模型)在圖1反饋關系的基礎上，結合經濟、人口，以及綜合運輸的特點，給出經濟-人口-運輸系統流圖，見圖2.

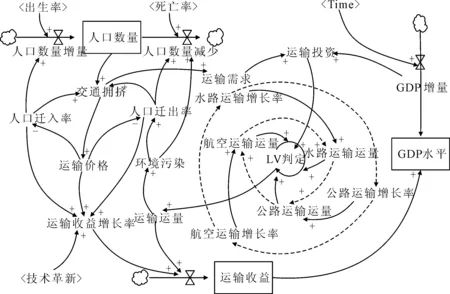
圖2 經濟-人口-運輸系統流圖

系統中包含的變量方程較多，篇幅所限，不一一列舉，可參見文獻[10-12].現將主要參數(見表1)及LV判定環中的方程列舉如下.

表1 主要參數

LV判定環方程：

Rs=Ry×fy+Rg×fg+RGDP×fgdp

Ry=R1+R2+R3+Rr×fr

R1=Rt×ft1+R2×f21+R3×f31

R2=Rt×ft2+R1×f12+R3×f32

R3=Rt×ft3+R1×f13+R2×f23

(1)

運輸系統中各種運輸方式間的作用系數需通過LV理論判定，這里對LV理論進行交通化改造，以運輸方式環中三種運輸方式來闡述系統的LV判定過程(即公路運輸、水路運輸及航空運輸)，令：x1，x2，x3為公路、水路及航空交通運輸方式的現有運輸需求量；k1，k2，k3為對應運輸方式在現有環境下的飽和容量指標，大于零為未飽和，小于零為過飽和；r1，r2，r3為三種交通運輸方式的單位增長率.

根據Lotka-Volterra理論，不同物種間的作用系數f，由物種間的影響比例與環境容納量決定，即f=α/k，公式重新定義如下：

αij為單位投資下運輸方式i對運輸方式j的影響比例(i、j=1、2、3,i≠j)；fij為運輸方式i對運輸方式j的作用系數，且fij=αij/kj，作用系數f的正負決定著反饋關系，其中正號為抑制作用，負號為促進作用.三種運輸方式隨時間的演化情況存在下列關系[13-15].

在這樣的合作競爭過程中，三種運輸方式的發展方向會隨著環境容納量ki、影響比例α的變化而變化.將式(2)進行簡化，令：

a1=r1，b1=r1/k1，c1=r1α12/k1，d1=r1α21/k1；a2=r2，b2=r2/k2，c2=r2α12/k2，d1=r2α32/k2；a3=r3，b3=r3/k3，c3=r3α13/k3，d3=r3α23/k3.得到式(3).

(3)

按照灰色模型的直接建模法，以xi(t+1)-xi(t)、[xi(t+1)+xi(t)]/2作為dxi/dt的白化值、背景值(i=1、2、3)，將式(3)進行離散化得式(4).

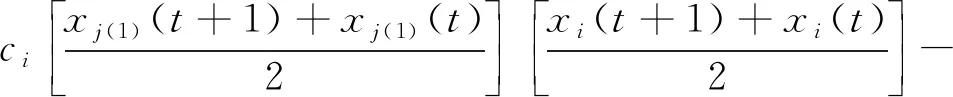
(i=1、2、3,j(1)=2、1、1,j(2)=3、3、2)

(4)

將t=1，2，…，n-1時的數據依次代入式(4)中得式(5).

? ? ? ? ?

(i=1、2、3,j(1)=2、1、1,j(2)=3、3、2)

(5)

(i=1,2,3;j(1)=2,1,1;j(2)=3,3,2)

(6)

比較式(5)和式(6)，可得：

運輸方式的增長率：ri=αi；

現有環境下的飽和容納量：ki=αi/bi；

影響比例：

α12=c2/b2，α13=c3/b3；α21=c1/b1，α23=d3/b3；α31=d1/b1，α32=d2/b2；

作用系數：

f12=c2/a2，f13=c3/a3；f21=c1/a1，f23=d3/a3；f31=d1/a1，f32=d2/a2.

2 案例分析

2.1 模型參數計算

利用Vensim軟件對LV-SD模型進行仿真，模擬重慶市綜合交通運輸系統中三種運輸方式的作用關系變化對GDP的影響，建立三維LV判定下的SD運輸系統，見表2.考慮到公路運輸的客運量占比過大，故選擇鐵路、水路及航空運輸進行分析.

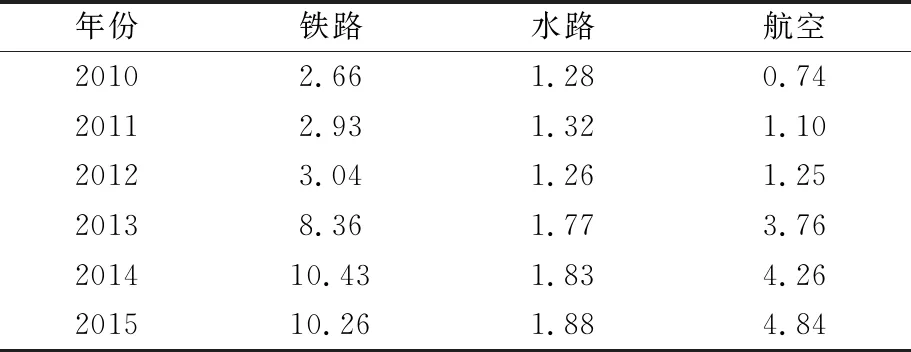
表2 模型參數值 單位：千萬人

鐵路客運量白化值為x1(t+1)-x1(t)，背景值為[x1(t+1)+x1(t)]/2；水路客運量白化值為x2(t+1)-x2(t)，背景值為[x2(t+1)+x2(t)]/2；航空客運量白化值為x3(t+1)-x3(t)，背景值為[x3(t+1)+x3(t)]/2.

將xi(t+1)-xi(t)、[xi(t+1)+xi(t)]/2代入矩陣中，經計算得出數據如下.

根據以上運算數據，現將運算結果整理如下.

鐵路運輸需求增長率ft1=r1=a1=1.678 212 962，鐵路運輸對水路運輸的作用系數f12=1.005 614 518，鐵路運輸對航空運輸的作用系數f13= 0.951 632 425.

水路運輸需求增長率ft2=r2=a2=-1.716 599 739，水路運輸對鐵路運輸的作用系數f21=2.034 201 16，水路運輸對航空運輸的作用系數f23=-0.379 563 8.

航空運輸需求增長率ft3=r3=a3=-2.055 530 424，航空運輸對鐵路運輸的作用系數f31=1.382 347 463；航空運輸對水路運輸的作用系數f32=-0.413 235 732.

將LV判定環中計算出的作用系數帶入系統動力學方程中，以2010年為基準年，參照文獻[13]中部分給出的方程數據，應用SPASS統計分析，獲取或標定上述動力學方程中的各個參數，見表3.其中關于GDP年增長率、人口出生死亡率及技術革新率等的作用系數，利用SPASS分析反復調試檢驗，再依據歷史經驗并結合專家建議獲得的綜合數值結果.

表3 2010年模型初始參數值

將系統中的常量數據代入方程，圖3為LV理論判定前后模型運輸方式子系統的關系變化.

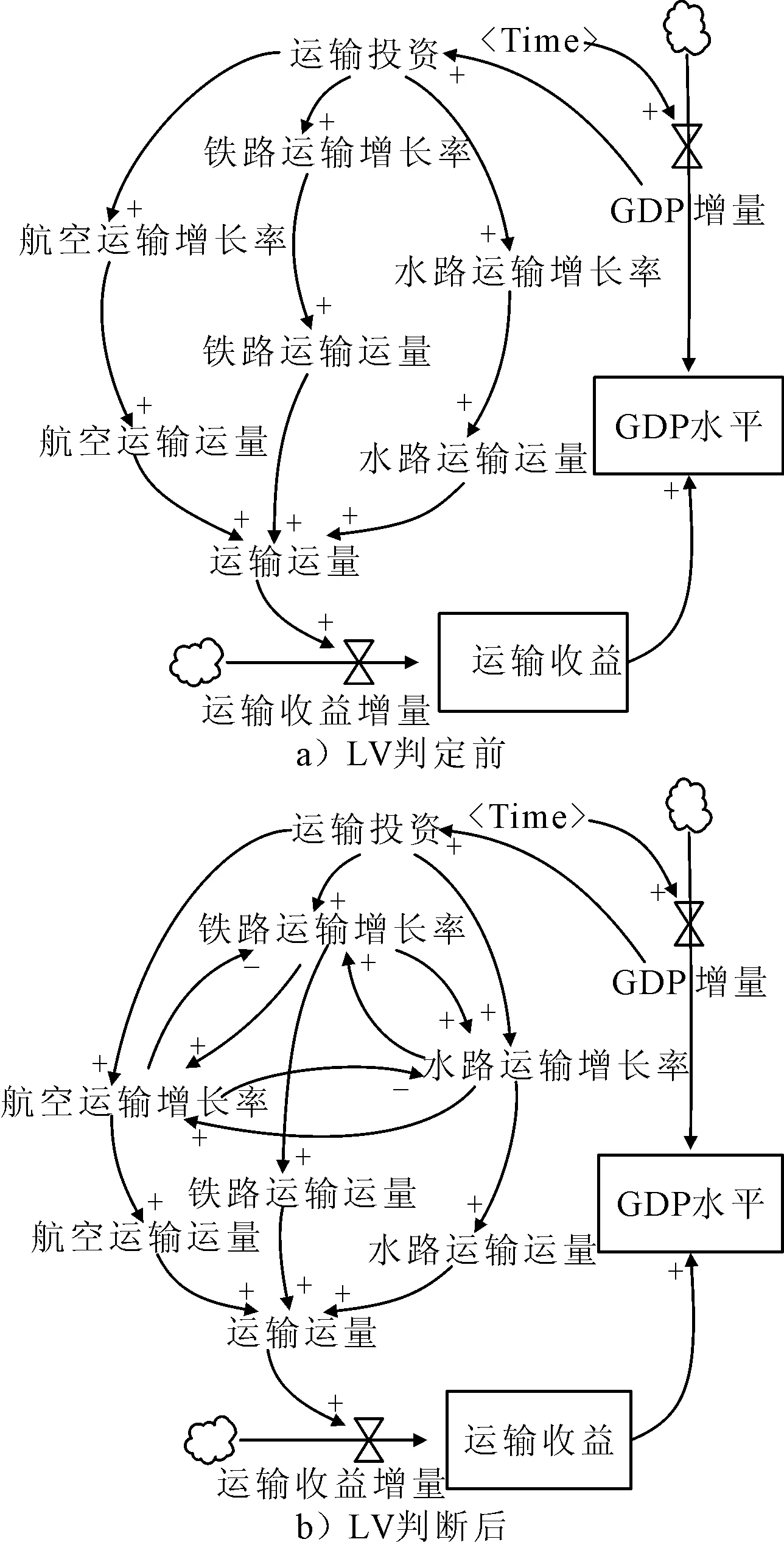
圖3 LV判斷前后運輸方式關系流圖

2.2 模擬結果與檢驗

通過LV-SD模型運行仿真，仿真結果對比SD模型以及歷史數據見表4.

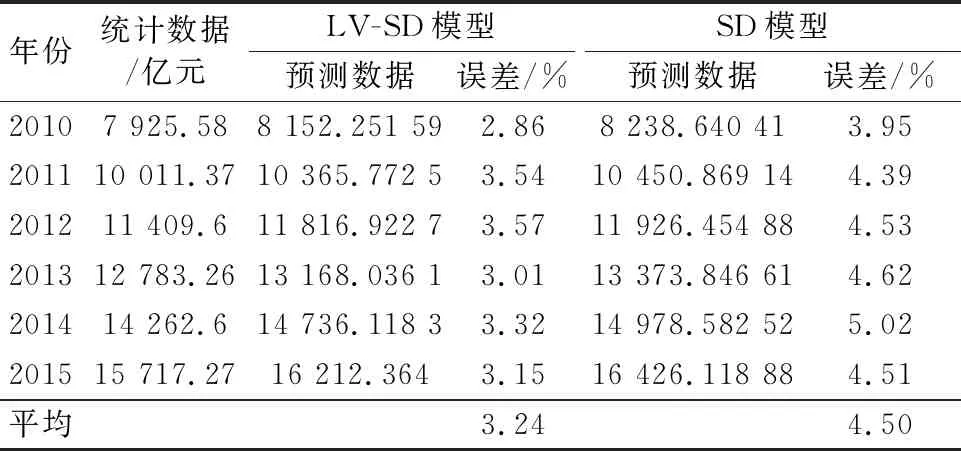
表4 GDP預測結果對比

由表4可知，觀察2010—2015年內GDP預測量與實際統計數據的誤差，LV-SD模型預測的歷年平均誤差為3.24%，SD模型預測的歷年平均誤差為4.50%，兩者較歷史數據而言，LV-SD模型預測精度提高了約1.26%，可見LV-SD模型較原有的SD預測模型預測精度有了近28%的提高.

3 結 論

1) 系統動力學模型中存在反饋關系不固定且隨著時間或空間維度處于不斷微變的反饋環.

2) Lotka-Volterra理論的引入證明了系統動力學模型反饋關系中存在隨時間細微變化的節點，節點的位置決定著反饋關系的正負與大小.Lotka-Volterra理論利用歷史累積數據，可以量化系統關系微變的節點，將復雜系統變量關系分割成模塊化的循環變化關系.

3) 短期預測中，系統反饋環中的關系不會出現大的變化，反饋關系可通過一次LV判定求得，而反饋節點需進行多次LV判定來確定節點區間位置；在長期預測中，為保證系統動力學模型的精度，需系統反饋環多次進行LV判定來保證變量關系的即時更新，因此判定次數倍數增長，過程復雜，體現不出具體的優勢，需對LV-SD模型做更深入的優化研究.

4) 基于專業領域的限制，LV判定下的SD模型節點研究僅以運輸系統為例，而未對其他領域進行驗證.需不同領域學者專家對LV-SD模型進行改進驗證.