面向多尺度決策形式背景的粒結構模型

陳應生，李進金，2，林榮德 ，陳東曉

1(華僑大學 數學科學學院 計算科學福建省高校重點實驗室，福建 泉州 362021)2(閩南師范大學 數學與統計學院，福建 漳州 363000)

1 引 言

在分析大量復雜信息時，基于有限的認識能力，人們通常會將龐大復雜的信息按照各自特點劃分為若干較為簡單的塊.被分出的每個塊就可以當作一個信息粒，以信息粒為單位，來分析處理復雜信息，這種方法稱為粒計算.自Zadeh[1，2]提出信息粒化的概念以來，粒計算得到了廣泛的關注[3-5]，隨著人工智能及大數據分析研究的不斷深入，粒計算理論得到不斷的完善和發展，并且在數據處理、機器學習、人工智能、圖像處理、模式識別等領域中具有廣泛的應用[6-13].

粗糙集是粒計算的經典模型，Yao在文獻[9]提出的利用等價關系構造信息粒的方法被廣泛的應用，由于人們處理信息的不同深度導致信息認識的不同粒度，Wu-Leung 在文獻[14]首次提出了多尺度決策信息系統，通過粒度轉換函數，給出了不同尺度間信息粒之間的轉化方法，并討論系統的知識獲取和最優尺度的選擇方法.隨后，文獻[15]提出不同屬性擁有不同尺度的推廣模型.文獻[16]提出了多尺度多決策的信息系統模型，并詳細討論決策屬性不同尺度間的粒度轉化，以及基于決策優先的最優尺度選擇.文獻[17-19]系統研究了不完備的多尺度決策信息系統模型，結合證據理論方法，討論了該系統的信息粒度、粗糙近似、知識提取和最優尺度組合的選擇方法.

利用分區進行信息造粒，這種方法過于嚴格，為了拓寬其應用，很多學者提出了推廣的模型，主要有覆蓋粗糙集模型[20]、模糊粗糙集[21]、形式背景[22-29]等等，其中形式背景是一個典型的推廣.文獻[22]指出形式概念分析是由對象集、屬性集以及它們之間的二元關系組成的完備格，通過二元關系定義算子，從而形成概念格.文獻[23-26]研究了形式背景概念格的生成方法、屬性約簡以及決策形式背景的協調性和屬性約簡.文獻[27]提出了粒協調的概念，討論決策形式背景的粒協調性質.文獻[28]系統比較決策形式背景的各種協調的關系.文獻[29]討論了概念格與覆蓋粗糙集的關系.指出形式背景和覆蓋粗糙集可以互相轉化.

在復雜信息和龐大數據中，形式背景產生的概念格十分復雜，因此，簡化概念，獲得適當規模大小的概念格是形式背景分析的重要問題之一，本文把多尺度信息系統的粒度轉化函數推廣到形式背景上來，引入多尺度形式背景，研究該系統的性質，以此為基礎，建立多尺度決策形式背景的理論框架，并研究它的協調性以及最優尺度選擇.

本文后面的安排如下.第2節介紹形式背景與決策形式背景的基本知識、各種協調性、以及它們的區別與聯系；第3節引入多尺度決策形式背景，并討論其粒結構和不同粒度間的粒度轉化關系、粗糙近似、不同尺度對應形式背景的各種協調關系；第4節引入多尺度決策形式背景，并研究各種協調的傳遞性，以及最優尺度選擇，并給出具體的算例；最后，我們總結這篇文章.

2 相關工作與基礎知識

針對多尺度形式背景問題，文獻[30]研究了多標記形式背景下的粒規則，其中要求每個對象在第i個標記Li下的取值是唯一的，這樣一個標記下的形式背景對應于論域的一個劃分，標記的每個取值以及取該值的對象全體匹配構成一個粒標記概念，即對任意的y∈Li，(f-1(y)，y)是一個概念(這里f-1(y)表示取值為y的對象全體)，由于它滿足f(f-1(y))=y.但對于集值信息系統或覆蓋信息系統，對象的標記取值可能不唯一，這時任意的y∈Li，不一定滿足f(f-1(y))=y，從而(f-1(y)，y)未必是一個概念.

Wu-Leung在文獻[14]中首次建立多尺度標記信息系統的粒計算模型，引入一個粒轉換函數來刻畫不同尺度間的信息粒關系，但在具體的應用中，屬性往往構成覆蓋而不是劃分，形式背景是對論域覆蓋的深入研究，文獻[29]中詳細討論覆蓋與形式背景的聯系.

為了使多尺度理論更適用于大數據和復雜信息的應用，本文把信息系統的粒度轉換函數推廣到形式背景上來，建立多尺度形式背景的粒計算模型.文獻[30]中的多標記形式背景模型為本文的特殊情況.

為了簡化表達，在本文中，我們把形式背景記為FC，決策形式背景記為FDC，多尺度形式背景記為MCFC，多尺度決策形式背景記為MCFDC.

本節我們介紹形式背景與決策形式背景的基本概念、性質和協調性.

2.1 形式背景

定義1[23].設(U，A，I)為一個形式背景(記為FC)，其中U={x1，x2，…，xn}為有限非空對象集，我們稱之為論域，A={a1，a2，…，am}為有限非空屬性集，I為U和A之間的一個二元關系，如果(x，a)∈I，則稱x具有屬性a，否則，稱x不具有屬性a.

如果把(x，a)∈I表示為1，把(x，a)?I表示為0，則形式背景就可以表示為一個布爾矩陣，記之為MI=(cij)n×m，其中：

設X?U，B?A，定義如下運算規則：

X*={a∈A|?x∈X，(x，a)∈I}，B*={x∈U|?a∈B，(x，a)∈I}.容易得到：

X*={a∈A|X?a*}=∩x∈Xx*，B*={x∈U|B?x*}=∩a∈Ba*.

如果，?x∈U，x*≠?，x*≠A且?a∈A，a*≠?，a*≠U，則稱(U，A，I)是正則的，下面我們所討論的FC都是正則的.

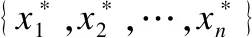
若X*=B，B*=X，則稱(X，B)是一個概念，(U，A，I)的所有概念記之為L(U，A，I).

LU(U，A，I)表示L(U，A，I)的概念外延構成的一個格，LA(U，A，I)表示由L(U，A，I)的概念內涵構成的一個格.

顯然，任意的X?U，(X**，X*)，是概念，同理任意的B?A，(B*，B**)也是概念，并且：

(X，B)=∪x∈X(x**，x*)，(X，B)=∩a∈B(a*，a**)

所以由對象粒概念(x**，x*)和屬性粒概念(a*，a**)通過并交運算可以生成FC的全體概念格.

對于(X1，B1)，(X2，B2)∈L(U，A，I)，定義運算:

(X1，B1)∧(X2，B2)=((X1∩X2)，(B1∪B2)**)

(X1，B1)∨(X2，B2)=((X1∪X2)**，B1∩B2)

在文獻[24，25]中，類似于粗糙集中的上下近似概念，對于任意的X?U，B?A，定義如下近似算子:X□={a∈A|a*?X}，X?={a∈A|a*∩X≠?}；B□={x∈U|x*?B}，B?={x∈U|x*∩B≠?}.

2.2 決策形式背景

定義2[25].設S=(U，A，I，D，J)為FDC，其中(U，A，I)與(U，D，J)是兩個FC.

如果(X，B)∈L(U，A，I)，(Y，C)∈L(U，D，J)，X?Y，且Y≠U、?，稱“B→C”是一個命題.

本文*A，**A表示(U，A，I)下的運算，同理*D，**D表示(U，D，J)下的運算.

決策形式背景由于系統復雜，對于它的協調性討論也是一個重要課題，下面介紹3種常用的協調性，并討論他們之間的關系.

定義3.設S=(U，A，I，D，J)是一個FDC:

1)[25].?(Y，C)∈L(U，D，J)，若存在(X，B)∈L(U，A，I)，滿足X=Y，則稱S是強協調的，記為L(U，A，I)≤L(U，D，J).

2)[25].?(Yi，Ci)∈L(U，D，J)，若存在(Xi，Bi)∈L(U，A，I)，使Xi?Yi，且Yi≠Yj時，有Xi≠Xj，則稱S是弱協調的，記為L(U，A，I)?L(U，D，J).

3)[27].x∈U，若有x**A?x**D成立，則稱S關于對象x是局部粒協調的，若S對所有對象都是局部粒協調的，則稱S是粒協調的.

文獻[28]詳細討論3種協調性之間的聯系，

1)強協調可以推出弱協調，但反之不成立；

2)由粒協調不能推出弱協調，反之也不成立；

3)強協調可以推出粒協調，反之不成立.

針對弱協調的判斷方法，文獻[25]給出了弱協調的等價定義.

推論1.L(U，A，I)?L(U，D，J)?存在單射f：LU(U，D，J)→LU(U，A，I)，滿足對?Y∈LU(U，D，J)，有f(Y)?Y.

特別地，如果LU(U，D，J)構成論域的一個劃分時，則粒協調就可以推出弱協調.

定理1.設S=(U，A，I，D，J)是粒協調的FDC，且{d*D|d∈D}

構成論域U的一個劃分，則有L(U，A，I)?L(U，D，J).

證明：我們利用定義3的推論1來證明.

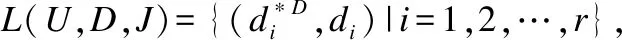
3 多尺度形式背景

3.1 多尺度形式背景

多尺度信息系統理論由Wu-Leung于文獻[14]中首次提出，文獻[15]提出了推廣的模型.根據文獻[14，15]的定義，對任意的屬性a∈A，a的m個尺度記為a1，a2，…，am，其中ak：U→Vk，Vk為a在第k個尺度下的值域，并且對于1≤k≤m-1，存在一個滿射gk，k+1：Vk→Vk+1，使得ak+1=gk，k+1°ak，即對任意的x∈U，有ak+1(x)=gk，k+1(ak(x))，稱gk，k+1為屬性ak到ak+1的粒度轉換函數.

上述定義要求ak：U→Vk是單值滿射的，但在具體的應用中，ak：U→Vk往往是多值的，即ak：U→P(Vk)，其中P(Vk)是Vk非空子集的全體，同樣的，我們要求對于1≤k≤m-1，也存在一個滿射gk，k+1：Vk→Vk+1，使得ak+1=gk，k+1°ak.

由此，我們提出如下多尺度形式背景的定義.

定義4.設(U，A，I)={(U，Ak，Ik)|k=1，2，…，m}為多尺度形式背景(記為MCFC)，其中A有m個尺度A1，A2，…，Am，相應地I也有m個尺度I1，I2，…，Im，并且每個(U，Ak，Ik)(k=1，2，…，m)都是一個FC，而且對任意的1≤k≤m-1，存在滿射映射gk，k+1：Ak→Ak+1，使得對任意的?x∈U，有x*Ak+1=gk，k+1(x*Ak)，gk，k+1稱為屬性集Ak到Ak+1的粒度轉換函數.

定理2.設(U，A，I)為一個MCFC，則對任意的x∈U，k∈{1，2，…，m-1}，有x**Ak?x**Ak+1.

證明：由于x**Ak={y∈U|x*Ak?y*Ak}，對任意的y∈x**Ak，有x*Ak?y*Ak，故而x*Ak+1=gk，k+1(x*Ak)?gk，k+1(y*Ak)=y*Ak+1，由x**Ak+1={y∈U|x*Ak+1?y*Ak+1}，所以y∈x**Ak+1，因此x**Ak?x**Ak+1.

注：由于任一概念(X，Bk)∈L(U，Ak，Ik)，有(X，Bk)=∪x∈X(x**Ak，x*Ak)，所以(x**Ak，x*Ak)是(U，Ak，Ik)中最細的信息粒.

定理2表明，在MCFC中，對應于較小尺度的最細信息粒較為精細.

并且，由于x**Ak?x**Ak+1，所以“x*Ak→x*Ak+1”是一個命題，說明，在較大尺度下最精細的命題可以由較小尺度下的命題推出.

特別地，當多尺度形式背景每個尺度對應的背景構成論域的一個劃分時，上述命題就是文獻[30]定義的粒標記規則.

定理3.設(U，A，I)為MCFC，則以下結論成立.

1)|Ak|≤|Ak+1|，其中|Ak|表示Ak中屬性的個數；

2)a∈Ak，b∈Ak+1若gk，k+1(a)=b，則a*Ak?b*Ak+1；

3)?b∈Ak+1，x∈b*Ak+1，存在a∈Ak，使得x∈a*Ak?b*Ak+1；

4)?b∈Ak+1，若(gk，k+1(b))-1=Bk，則b*Ak+1=∪a∈Bka*Ak.

證明：

1)直接由粒度轉換函數gk，k+1的定義可得.

2)?x∈a*Ak，有a∈x*Ak，由于gk，k+1(x*Ak)=x*Ak+1，所以b=gk，k+1(a)∈x*Ak+1，故而x∈b*Ak+1，因此a*Ak?b*Ak+1.

3)?b∈Ak+1，有b∈x*Ak+1，由gk，k+1(x*Ak)=x*Ak+1，所以存在a∈x*Ak，使得gk，k+1(a)=b，由(2)得a*Ak?b*Ak+1，所以x∈a*Ak?b*Ak+1.

4)對任意的a∈Bk，有gk，k+1(a)=b，所以a*Ak?b*Ak+1，故而∪a∈Bka*Ak?b*Ak+1，另一方面，對?x∈b*Ak+1，有b∈x*Ak+1，由于(gk，k+1(b))-1=Bk，存在a∈Bk，使得gk，k+1(a)=b，由b∈x*Ak+1和gk，k+1(x*Ak)=x*Ak+1，所以a∈x*Ak從而x∈a*Ak，所以x∈∪a∈Bka*Ak，故而b*Ak+1?∪a∈Bka*Ak，所以b*Ak+1=∪a∈Bka*Ak.

注：定理3說明

1)MCFC對應尺度k的形式背景(U，Ak，Ik)，任意的a∈Ak，(a*Ak，a**Ak)是一個概念，當Ak構成論域的一個劃分時，有a**Ak=a，此時(a*Ak，a)就是文獻[30]所提的標記概念.

2)若(gk，k+1)-1=Bk，則有b*Ak+1=∪a∈Bka*Ak，

所以，當每個尺度的屬性集都構成論域的劃分時，定義4就是文獻[30]所提的多標記背景定義.

3)如果gk，k+1(a)=b，則 “a**Ak→b**Ak+1”是一個命題，當每個尺度的形式背景都構成論域 的劃分時，有a**Ak=a，b**Ak+1=b，所以命題“a**Ak→b**Ak+1”簡化為“a→b”就是文獻[30]中所提的對象如果在屬性a下的值相等，則在屬性b下的值也是相等的.

定理4.設(U，A，I)為MCFC，則有以下結論成立.

1)任意(Y，C)∈L(U，Ak+1，Ik+1)，一定存在(X，B)∈L(U，Ak，Ik)，使得X?Y，即“B→C”是一個命題；

2)任意(X，B)∈L(U，Ak，Ik)，一定存在(Y，C)∈L(U，Ak+1，Ik+1)，使得X?Y，即“B→C”是一個命題.

證明：

1)任意的(Y，C)∈L(U，Ak+1，Ik+1)，滿足Y*Ak+1=C，并且C*Ak+1=Y，對任意的b∈C，存在a∈A，使得a*Ak?b*Ak+1，所以Y=C*Ak+1=∩b∈Cb*Ak+1?∩a∈Ba*Ak=B*Ak，取(B*Ak，B**Ak)∈L(U，Ak，Ik)，X=B*Ak，即可.

2)任意的(X，B)∈L(U，Ak，Ik)，滿足X*Ak=B，并且B*Ak=X，對任意的a∈A，存在b∈C，使得a*Ak?b*Ak+1，所以B*Ak=∩a∈Ba*Ak?∩b∈Cb*Ak+1=C*Ak+1，取(C*Ak，C**Ak)∈L(U，Ak+1，Ik+1)，Y=C*Ak+1即可.

定理4說明，在MCFC中，較大尺度規模下的一個結論，總可以由較小尺度下的條件推得.

3.2 多尺度形式背景的粗糙近似算子

MCFC對應尺度k的FC為(U，Ak，Ik)，?X?U，Bk?Ak，根據近似算子的定義，有:

X□k={a∈Ak|a*Ak?X}，X?k={a∈Ak|a*Ak∩X≠?}；

B□k={x∈U|x*Ak?Bk}，B?k={x∈U|x*Ak∩Bk≠?}.

定理5.設(U，A，I)為MCFC，則以下結論成立:

1)gk，k+1(X□k)?X□k+1；

2)gk，k+1(X?k)?X?k+1；

3)如果gk，k+1(Bk)=Bk+1，則有B□k?B□k+1；

4)如果gk，k+1(Bk)=Bk+1，則有B?k?B?k+1.

證明：

1).對任意的b∈X□k+1，則有b*Ak+1?X，?a∈(gk，k+1b)-1，則gk，k+1(a)=b，由定理3(2)，a*Ak?b*Ak+1，故而a*Ak?X，故而(gk，k+1(X□k+1))-1?X□k，因此gk，k+1(X□k)?X□k+1.

2)?a∈X?k，有a*Ak∩X≠?，設b=gk，k+1(a)，由定理3(2)，a*Ak?b*Ak+1，故b*Ak+1∩X≠?，因此gk，k+1(X?k)?X?k+1.

3)?x∈B□k+1，有x*Ak+1?Bk+1，根據gk，k+1(x*Ak)=x*Ak+1以及gk，k+1(Bk)=Bk+1，故而x*Ak?Bk，所以x∈B□k，因此B□k?B□k+1；

4)?x∈B?k，有x*Ak∩Bk≠?，由gk，k+1(x*Ak)=x*Ak+1及gk，k+1(Bk)=Bk+1，所以x*Ak+1∩Bk+1≠?，故而x∈B?k+1，從而B?k?B?k+1.

3.3 多尺度形式背景尺度間的協調關系

如果把(U，Ak，Ik，AK+1，Ik+1)當作一個FDC，由定理2有x**Ak?x**Ak+1，根據定義3粒協調的定義，有如下結論成立.

定理6.設S=(U，A，I)為MCFC，則(U，Ak，Ik，Ak+1，Ik+1)是粒協調的.

例1.(U，Ak，Ik，Ak+1，Ik+1)未必是弱協調的，如表1所示的MCFC(U，A，I)=(U，{A1，A2}，{I1，I2})，其中:

A1={a，b，c，d，e}，A2={g，h，k}

粒度轉換函數g12：A1→A2為:

形式背景的布爾矩陣表如表1所示.

表1 多尺度決策形式背景1Table 1 Multi-scale formal context 1

經計算，L(U，A2，I2)={(U，?)，(12，h)，(13，g)，(24，k)，(1，gh)，(2，hk)，(?，A)}；L(U，A1，I1)={(U，?)，(2，be)，(13，a)，(4，d)，(1，ac)，(?，D)}，由于不存在單射f：LU(U，D，J)→LU(U，A，I)，滿足對任意的Y∈LU(U，D，J)，有f(Y)?Y，所以，(U，A1，I1，A2，I2)不是弱協調的.

定理6及例1這表明多尺度形式背景較小尺度對于較大尺度，只能滿足粒協調，不能滿足弱協調，更不能保證強協調.

4 多尺度決策形式背景

定義5.設S=(U，A，I，D，J)為一個多尺度決策形式背景(記為MCFDC)，這里(U，A，I)={(U，Ak，Ik)|k=1，2，…，m}為一個MCFC，D≠Ai(i=1，2，…，m)，且(U，D，J)是一個FC.

由定義5可得，一個MCFDC包含m個FDC，把對應第k(k=1，2，…，m)尺度的FDC記為Sk=(U，Ak，Ik，D，J).

定理7.設S=(U，A，I，D，J)為MCFDC，(Y，C)∈L(U，D，J)，若(Xl，Bl)∈L(U，Al，Il)，使得Bl→C是一個命題，則對任意的k≤l，存在(Xk，Bk)∈L(U，Ak，Ik)，使得Bk→C也是一個命題.

證明：由定理4直接可得.

定理7表明，如果較粗的尺度規模下能夠成立的，則在較細的尺度規模下也一定成立.

4.1 多尺度決策形式背景的協調性

設S=(U，A，I，D，J)為MCFDC，第k尺度的FDC記為Sk=(U，Ak，Ik，D，J)，首先我們討論粒協調，由定理2及定理6，易得如下定理.

定理8.設S=(U，A，I，D，J)是MCFDC，則有以下結論成立.

1)Sk關于x∈U是局部粒協調的充要條件是x**Ak?x**D，Sk是粒協調的充要條件是對任意的對象都是局部粒協調的；

2)如果Sk關于x是局部協調的，則對任意的l≤k，Sl關于x也是局部協調的；

3)如果Sk是粒協調的，則對任意的l≤k，Sl也是粒協調的.

由定理8可得，MCFDC的粒協調滿足傳遞性，例2說明MCFDC的強協調與弱協調并不一定滿足傳遞性，例2.弱協調不一定具有傳遞性.

如表2所示的MCFDCS=(U，A，I，D，J)，其中(U，A，I)為例1中表1對應的MCFC，決策屬性集為D={X，Y，Z}，系統對應的布爾矩陣為表2.

表2 多尺度決策形式背景2Table 2 Multi-scale formal decision context 2

由例1的結論，得(U，A1，I1，A2，I2)不是弱協調的，即L(U，A1，I1)?L(U，A2，I2)不成立，由于L(U，A2，I2)=L(U，D，J)，所以L(U，A1，I1)?L(U，D，J)不成立.

由例2說明，弱協調不一定具有傳遞性，同理可以得到強協調也不一定具有傳遞性.

特別地，當決策背景形成一個劃分時，下面定理說明，弱協調也具有傳遞性.

定理9.設S=(U，A，I，D，J)是MCFDC，并且{d*D|d∈D}構成U的一個劃分，如果L(U，Ak+1，Ik+1)?L(U，D，J)，則有L(U，Ak，Ik)?L(U，D，J).

證明：利用定義3的推論1來證明.

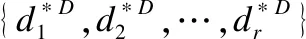
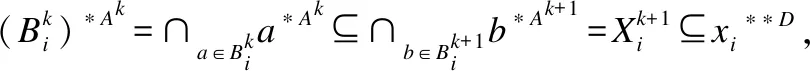
4.2 多尺度決策形式背景的最優尺度選擇

設S=(U，A，I，D，J)是一個MCFDC，較小尺度對應的FDC所表達的知識的精度較高，但卻需要花費較多時間和精力去了解知識，而較大的尺度雖然表達的知識比較粗糙，但卻可以花費較少的時間和精力去了解知識，在具體的應用過程中，我們希望利用較少信息得到理想的決策，由此，提出MCFDC的最優尺度選擇.

由于在多尺度決策形式背景中，強協調不具有傳遞性，粒協調具有傳遞性，在決策是劃分的情況下，弱協調也具有傳遞性，所以本節只討論保粒協調的最優尺度選擇和保弱協調的最優尺度選擇.

4.2.1 粒協調下的最優尺度選擇

定義6.設S=(U，A，I，D，J)為一個MCFDC，若S1是粒協調的，則稱S是粒協調的，若存在k∈{1，2，…，m}，使得Sk是粒協調的，但Sk+1不是粒協調的，則稱k是粒協調最優尺度.

定義7.設S=(U，A，I，D，J)為一個MCFDC，x∈U，若存在k∈{1，2，…，m}，使得Sk關于x是局部粒協調的，但Sk+1關于x不是局部粒協調的，則稱k是關于x局部粒協調最優尺度.

例3.求表3所示的MCFDC的保持粒協調得最優尺度.

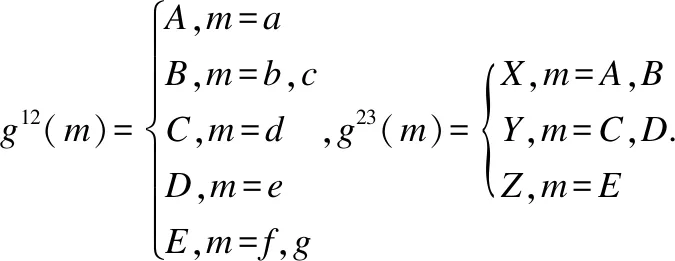
形式背景的布爾矩陣表如表3所示.

表3 多尺度決策形式背景3Table 3 Multi-scale formal decision context 3

經計算，可得：

1)1**D={1}，2**D=4**D={2，4}，3**D={3}；

2)1**A3={1，3}，2**A3=4**A3={2，4}，3**A3={3}；

3)1**A3={1}，2**A3=4**A3={2，4}，3**A3={3}.

所以尺度2是粒協調的最優尺度選擇，并且該系統是粒協調的.對于局部粒協調，對象2，3，4局部粒協調的最優尺度是3，而對象1局部粒協調的最優尺度是2.

4.2.2 弱協調下的最優尺度選擇

在MCFDC中，對于弱協調，通常是不保持傳遞性的，由定理9，當決策是劃分時，弱協調也具有傳遞性，所以我們可以只討論決策是劃分時的保弱協調的最優尺度選擇.

定義8.設S=(U，A，I，D，J)為一個MCFDC，并且L(U，D，J)構成論域的一個劃分，若S1是弱協調的，則稱系統S是弱協調的，更進一步，如果L(U，Ak，Ik)?L(U，D，J)，但L(U，Ak+1，Ik+1)?L(U，D，J)不成立，則稱k是S的保弱協調的最優尺度.

例4.求表3所示的MCFDC的保弱協調的最優尺度.

經計算得:

L(U，D，J)={(?，D)，(1M)，(24，P)，(3，Q)，(U，?)}；L(U，A3，I3)={(?，A3)，(13，Y)，(124，X)，(3，XY)，(24，XZ)，(U，?)}.L(U，A2，I2)={(?，A2)，(1，CD)，(13，D)，(234，B)，(3，ABD)，(24，BE)，(?，A)}(U，?)}.經計算，L(U，A3，I3)?L(U，D，J)不成立，L(U，A2，I2)?L(U，D，J)，所以第2尺度是保弱協調的最優尺度.

定理10.設S=(U，A，I，D，J)是一個MCFDC，當L(U，D，J)構成論域的一個劃分時，并且系統S是粒協調的，如果k是粒協調的最優尺度，l是弱協調的最優尺度，則k≤l.

證明：由于決策構成一個劃分，由定理1得，該多尺度決策形式背景也是弱協調的，所以存在弱協調的最優尺度，Sk是粒協調的，所以Sk也是廣義協調的，所以k≤l.

5 總 結

多尺度信息系統的粒度轉換函數刻畫了多粒度信息從粗到細的特點，本文將這個粒度轉換函數推廣引入到FC中，建立了MCFC粒計算模型，以此來描述MCFC不同尺度之間的概念信息粒關系，不同尺度間粗糙近似算子的關系，以及不同尺度對應形式背景的協調性.在此基礎上，引入MCFDC，并討論它的協調傳遞性，通過分析，強協調和弱協調都不一定滿足傳遞性，粒協調滿足傳遞性，特別地，當決策是劃分時，弱協調也滿足傳遞性.最后，我們分別研究了MCFDC保持粒協調和弱協調的最優尺度選擇，并給出具體的算例.本文建立了MCFDC的理論框架，推廣了多尺度決策信息系統和多粒度形式背景的粒計算模型，未來，我們將研究MCFDC的規則提取和引入多尺度多決策的形式背景.