大跨越輸電塔線體系斷線響應分析

張健琦，張德凱，鄧洪洲

（同濟大學，上海 200092）

0 引言

強風、雷電、覆冰、電線的疲勞均可以導致線路發生斷線事故，造成供電中斷、斷線倒塔等事件［1］。輸電線路工程是電力系統建設的重要環節［2］，自立式輸電塔屬于柔性結構［3］，即便斷線事故并不是一個大概率事件，但是一旦發生，不僅會造成電氣設備的損壞，嚴重時甚至會造成輸電塔連續倒塌。對于大跨度的輸電塔線體系來說，這種破壞會造成整個輸電塔線體系的癱瘓和巨大的經濟損失。

斷線事故發生時會產生極大的不平衡張力，對輸電塔線體系產生巨大的沖擊作用，使輸電塔產生較大的內力和位移響應，對于大跨度輸電塔線體系來說，這種沖擊作用帶來的危害更加明顯。但我國目前的架空輸電線路設計規范和標準［4］還未考慮斷線的動力沖擊作用，這是存在安全隱患的。

國內外學者在斷線方面的研究始于20 世紀70年代，Mozer 等［5］通過簡化物理模型提出了分析輸電塔線體系不平衡張力的具體步驟；John 編制了計算程序，用于分析一根或多根導（地）線斷裂時對輸電塔線體系的動力沖擊［6］；夏正春等［7］采用等效彈簧替代輸電塔用以獲得輸電塔線體系的動態響應；李黎等［8］借助了ANSYS/LS-DYNA，采用非線性動力有限元的方法，研究了輸電塔線體系單根導線斷線響應和初張力、檔距、絕緣子等參數的關系。上述研究運用了非線性動力有限元分析了斷線工況下輸電塔線體系的動態響應，但對于耐張段的長短影響，導線、地線不同斷線工況的差異，以及斷線工況下對于輸電塔構件內力影響缺少研究，且未與靜力計算的規范結果進行比較。

借助有限元程序ANSYS，采用非線性隱式動力分析有限元的方法，研究大跨越輸電塔線體系單根導（地）線斷線對輸電塔線體系的沖擊響應，研究耐張段的長短影響，導線、地線不同斷線工況，斷線工況下對于輸電塔構件內力影響，將動力分析的結果與靜力計算的規范結果進行比較，以便為今后線路設計提供參考。

1 理論分析與假定

1.1 基本假定

研究大跨越輸電塔線體系在斷線下的響應，有限元模型有如下假定：

1）考慮幾何非線性，材料符合胡克定律；

2）導（地）線采用多段只能受拉不能受壓的兩節點直線桿單元模擬，地線夾具、絕緣子串采用兩節點的直線桿單元模擬；

3）導（地）線單元之間、導線與絕緣子串、地線與地線夾具之間均采用理想鉸接；

4）斷線點處于絕緣子與導線或地線夾具與地線連接處；

5）按照等面積等剛度原則，將分裂導線等效為一根整體導線，斷裂時認為子導線同時斷裂。

1.2 理論分析

1）輸電塔線體系在重力作用下處于平衡狀態，此時導（地）線存在張力，采用非線性靜力分析，基本方程為

式中：d為節點位移向量，會隨著時間t的變化而變化；K為結構剛度矩陣，由于幾何大變形呈非線性，剛度矩陣隨著節點位移向量d的變化而變化；W為自重等效節點荷載向量，由于斷裂的導（地）線在重力的作用下跌落，存在幾何大變形，會隨著時間t的變化而變化。

2）在初始平衡的條件下，導（地）線斷線內力瞬間移除，導（地）線釋放應變勢能，對體系產生激勵，使體系在此激勵下做阻尼自由振動，采用非線性動力分析，基本方程為

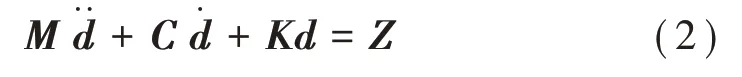
3）隨后，斷裂的導（地）線在重力的作用下跌落，使體系在重力的作用下做有阻尼的受迫振動，采用非線性動力分析，基本方程為：

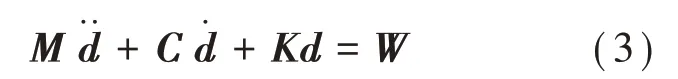
2 輸電塔線體系的有限元建模

該大跨越輸電塔跨越塔高266 m，呼高244 m，塔體形狀為“干”字型，基底根開為51.64 m，跨越塔為雙回路三角排列；錨塔高度66 m，呼高34 m，單回路垂直排列。塔線體系的有限元模型如圖1 所示，定義X向為塔線體系垂直導線方向，Y向為塔線體系順導線方向，Z向為輸電塔豎直方向。輸電塔主跨越段跨度為2 500 m，弧垂為214 m，兩耐張段的跨距為790 m 和557 m，弧垂分別為22.7 m 和11.9 m。地線夾具與導線絕緣子串長度分別為1.0 m 和7.8 m，導線為三分裂JLHA4/G5A-500/230 鋼芯鋁合金絞線，地線為光纜OPGW-308，48 芯。導線及地線物理力學參數如表1所示。

表1 導線及地線參數

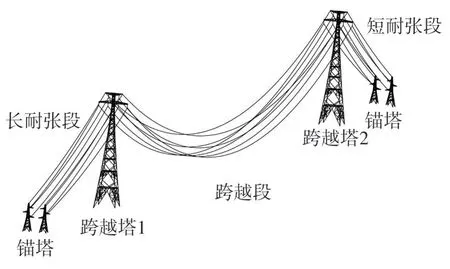
圖1 輸電塔線體系的有限元模型

建立輸電塔線體系的有限元模型，模型包括4個錨塔、2 個跨越塔、導線和地線、絕緣子等，為簡化計算，將爬梯、節點板、間隔棒、阻尼線等簡化成附加質量作用在輸電塔線體系上；塔下的基礎剛度很大，在建模時將4 個塔腳的自由度全部約束；導（地）線所受到的重力荷載沿導（地）線的弧長均勻分布，此時導（地）線的形狀為懸鏈線［9］，當垂度小于1/9 時，懸鏈線和拋物線差別很小，二者誤差可為工程所接受，故導（地）線的形狀模型采用拋物線。

3 導（地）線斷線的有限元模擬

輸電塔線體系的斷線模擬采用如下的步驟：

1）輸電塔線體系在重力的作用下保持平衡，并使各個構件產生內力；

2）突然斷線采用有限元中的生死單元法來模擬，導（地）線的斷裂是突然發生的，斷線在極短的時間內發生，斷線時間認為是10-8s，斷線后認為斷線處的導（地）線張力瞬間線性移除；

3）在斷線時程分析中，荷載步步長為0.01 s，采用自動時間步長，最小子步長為10-8s，時間長度取20 s；

4）輸電塔線體系采用瑞利阻尼，阻尼比取0.02［10］，瑞利阻尼矩陣計算公式為

式中：ɑ為Alpha 阻尼，也稱阻尼質量系數；β為Beta阻尼，也稱剛度阻尼系數［11］。

4 輸電塔線體系的斷線響應分析

研究在斷一根導（地）線的情況下輸電塔線體系的斷線響應特性，斷線點處于跨越段邊緣時，最為不利［8，12-13］，限于篇幅，只研究斷線點處于跨越段邊緣的工況。由于該體系順導線方向對稱，且兩個耐張段的距離不等，故共有8 種工況，為方便敘述，將各種工況進行編號。先對跨越塔進行編號，沿Y 軸正方向，將跨越塔分為跨越塔1 和跨越塔2，導線與地線位置及編號如圖2 所示。以編號“導線2-3”為例，“導線”表示斷線為導線，2 表示斷點在跨越塔2 處，3表示斷點在導線3 上，故若僅斷一根線，共有“導線1-1”“導線1-2”“導線1-3”“地線1”“導線2-1”“導線2-2”“導線2-3”“地線2”8種工況。對絕緣子及地線夾具進行編號，與斷線工況類似，以“絕緣子2-1”為例，2 表示在跨越塔2 上的絕緣子，1 表示與導線1 連接的絕緣子。斷線位置如圖3所示。

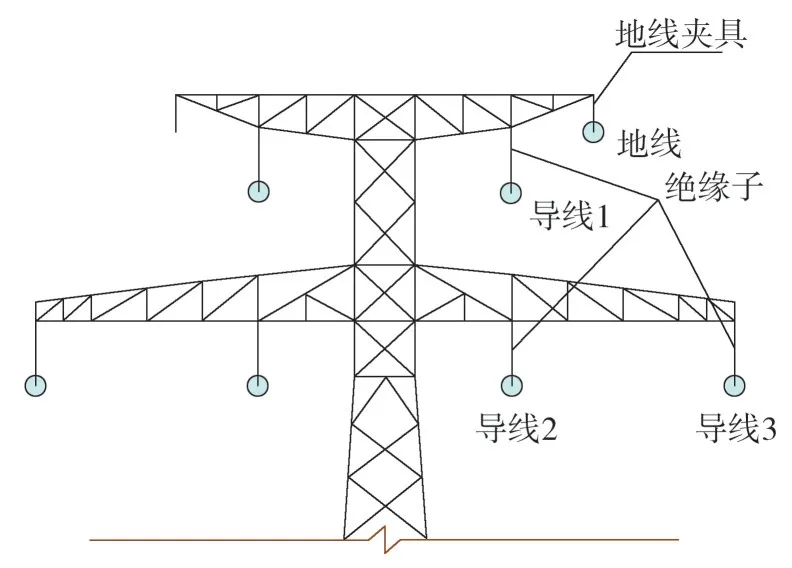
圖2 導線與地線位置和編號

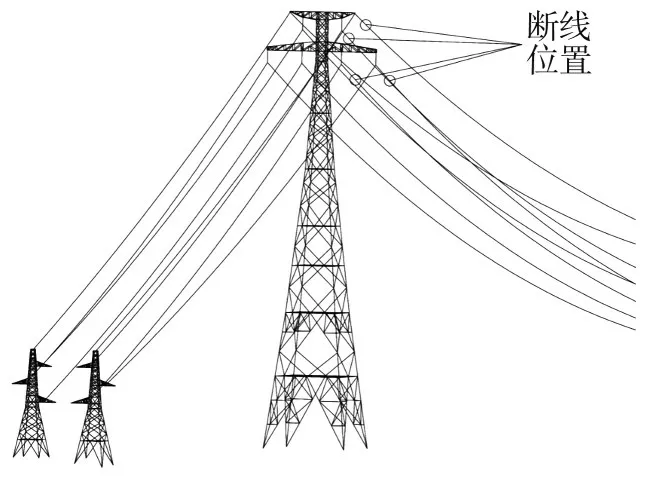
圖3 輸電塔線體系局部視圖

4.1 位移響應分析

由于不同工況下的位移響應類似，限于篇幅，僅列舉出導線1-1、導線2-1 和地線1、地線2 這4 種工況下絕緣子（地線夾具）下端與導線（地線）相連接點的三向位移圖，如圖4 所示。在導線跌落的過程中，與斷線相連的跨越塔的絕緣子發生了大幅擺動，由初始時刻的豎直位置變成了接近水平的傾斜位置，而后在一個固定值附近擺動。

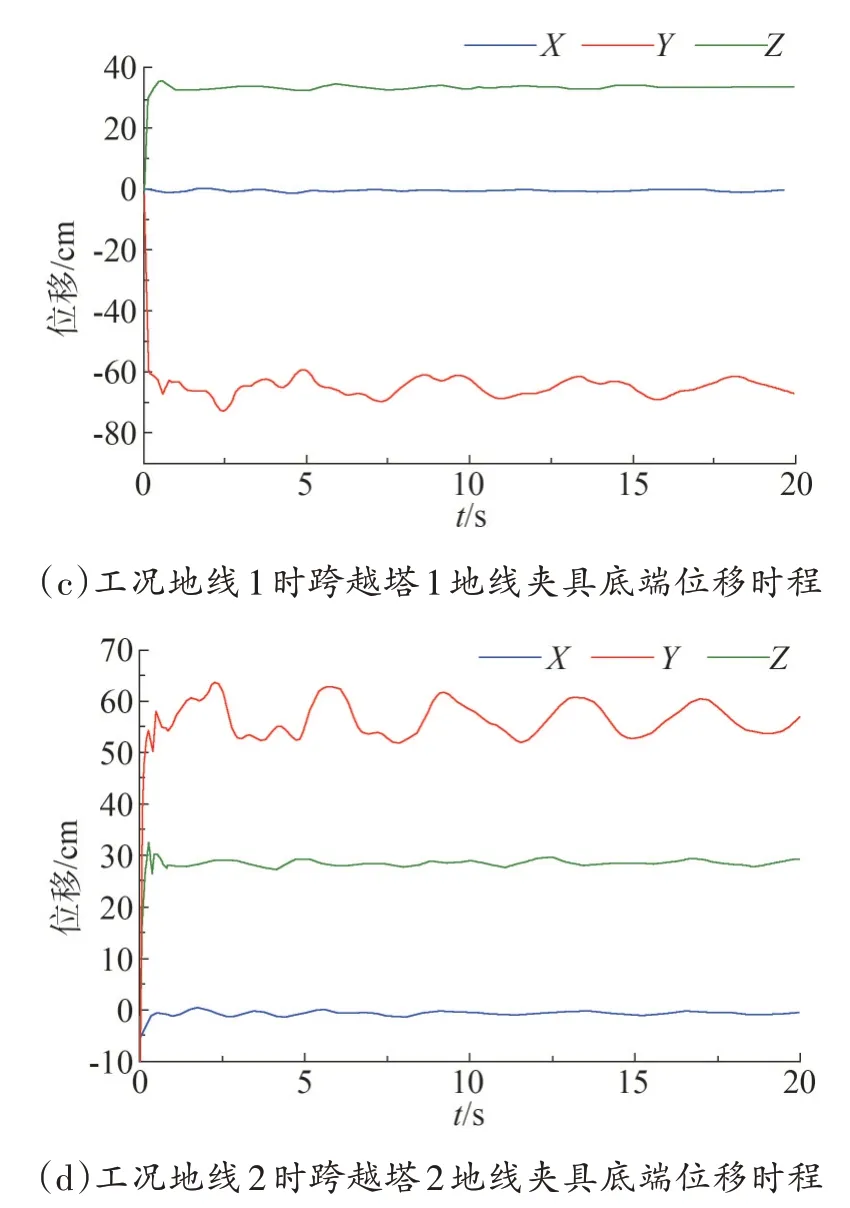
圖4 不同工況下絕緣子及地線夾具底端三向位移時程

當斷線點在跨越塔1 上的導線上時，絕緣子在高度方向（Z方向）向上擺動，最大擺幅約為5.6 m，在順導線方向（Y方向）做遠離跨越塔的運動，最大擺幅約為7.8 m，Y方向和Z方向的最大擺幅幾乎同時出現，出現時間大概為1.2 s，在大概4 s 后，絕緣子的擺動變得緩慢。

當斷線點在跨越塔1 的地線上時（即工況地線1），由于地線夾具的長度較小，3 個方向的位移尺度都遠小于絕緣子，地線夾具在高度方向（Z方向）上向上擺動，最大擺幅約為37 cm，在達到最大擺幅后，Z方向的位移達到穩定，在順導線方向（Y方向）做遠離跨越塔的運動，最大擺幅約為76 cm，Y方向的最大擺幅時間為2.5 s，略微滯后于Z方向的最大擺幅時間0.3 s；當斷線點在跨越塔2 的地線上時（即工況地線2），上述規律依然成立，且發生最大擺幅的時間一致，但數值上略小于地線1 工況，Y方向的最大擺幅為64 cm，Z方向的最大擺幅為33 cm。

綜上，可以發現，斷線對靠近長耐張段的位移響應較大。雖然輸電塔線體系不存在沿X方向（垂直導線方向）的擾動，但斷線處與絕緣子點還是在X方向存在著微小的振動，這是由于斷線使跨越塔的受力不平衡，使跨越塔產生了繞Z方向的扭轉。

4.2 軸力響應分析

4.2.1 絕緣子軸力響應分析

在跨越段的每根導線左右兩端連接著2 個絕緣子，在一側發生斷線時，對連接該導線兩端的絕緣子都存在著沖擊作用，由于各種工況下的時程圖相類似，僅給出工況導線1-1、導線2-1 下2 個絕緣子的軸力時程，如圖5所示。

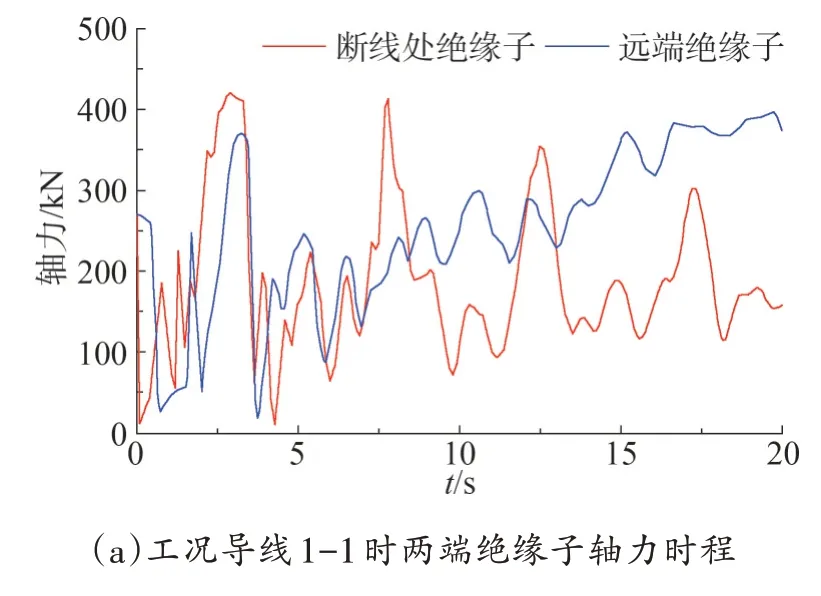
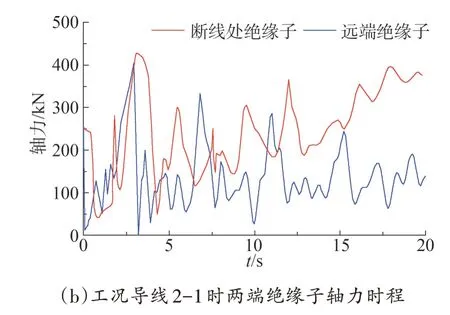
圖5 不同工況下絕緣子軸力時程

由圖5 可觀察到，兩個軸力時程曲線有明顯的波動狀態，且在計算的工況下，斷線處的絕緣子在斷線后的0.1 s時間內軸力先迅速減小，而后逐漸變大，在接近t=2.5 s 的時候達到極大值，時間滯后于Y、Z方向位移的峰值，而后隨著時間的變化峰值逐漸衰減；斷線遠端的絕緣子在斷線后的前0.3 s 軸力保持不變，后迅速減小到t=1 s 時刻，之后逐漸增大到第一個峰值后逐漸減小，在t=4.3 s到達低點，而后呈周期性地逐漸增大，甚至會超過第一個峰值。斷線處的絕緣子隨著時間的變化峰值逐漸衰減是由于阻尼的作用；斷線遠端的絕緣子在斷線后的前0.3 s 軸力保持不變是由于斷線的沖擊作用傳遞到遠端的輸電塔需要一定的時間，而斷線遠端的絕緣子后期呈周期性逐漸增大是由于導線的掉落落重力牽拉以及阻尼的共同作用。

引入動力系數η［14-15］

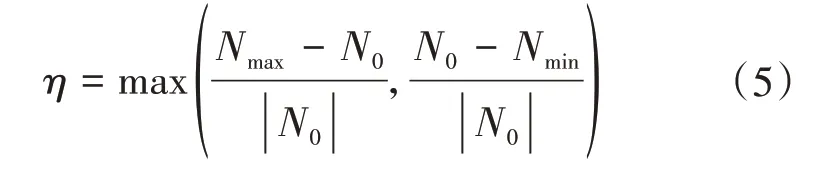
式中：N0為只受重力作用下桿件的軸力值；Nmax為桿件在斷線工況下的軸力最大值；Nmin為桿件在斷線工況下的軸力最小值。

不同工況下絕緣子的動力系數η如表2 所示。可以發現，在相同工況下，靠近長耐張段的絕緣子最大力要略大于靠近短耐張段的絕緣子；相同工況下，斷線處的絕緣子動力系數要略大于遠端絕緣子的動力系數；對于同一絕緣子，在靠近該絕緣子處斷線的動力系數較大。

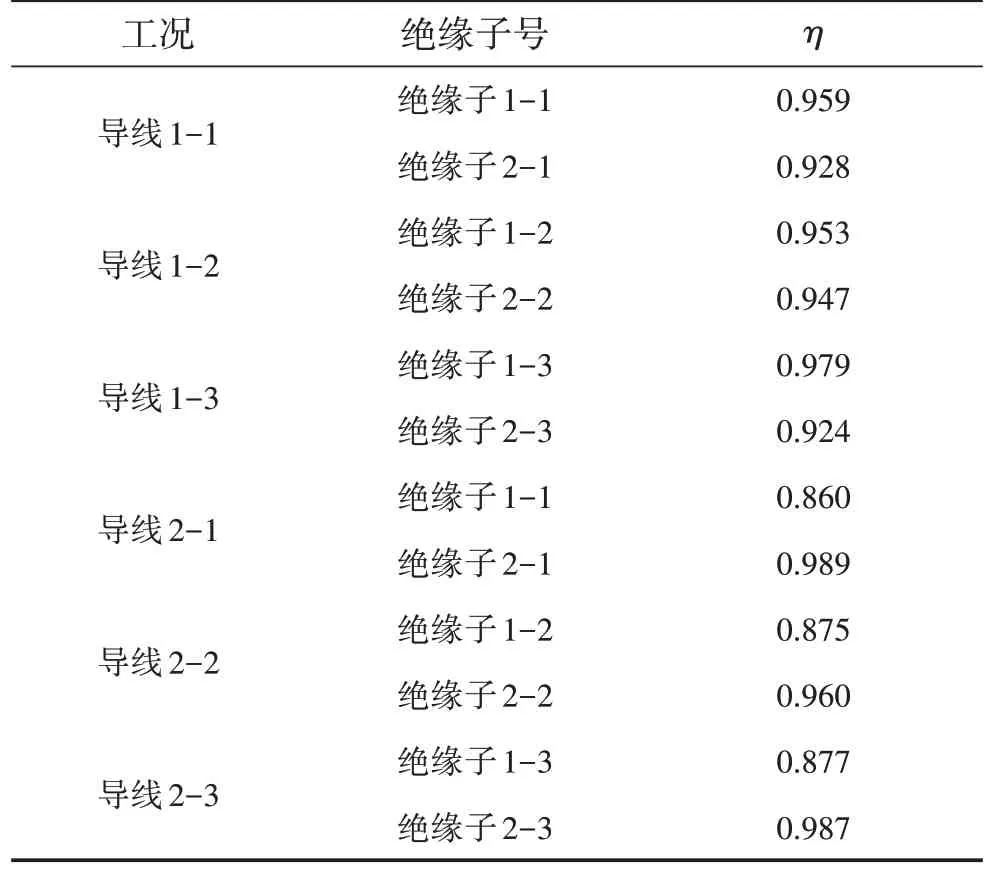
表2 不同工況下絕緣子的動力沖擊系數η

4.2.2 地線夾具軸力響應分析

由于地線1 和地線2 兩種工況時地線夾具的軸力時程相類似，以工況地線1 為例，給出地線夾具的軸力時程如圖6 所示。可觀察到地線夾具軸力時程規律與絕緣子相類似；同時可以發現，重力對遠端的地線夾具作用相當大，會超出第一個峰值。

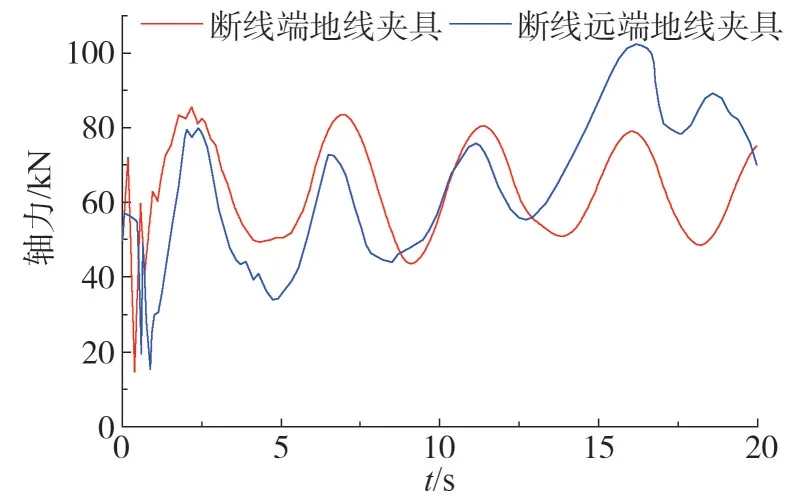
圖6 地線夾具軸力時程

不同工況下地線夾具的動力系數η如表3所示。可以觀察到地線夾具的動力系數會小于絕緣子的動力系數，且與絕緣子不同，斷線遠端的地線夾具的動力沖擊要大于斷線處的地線夾具，對于同一地線夾具在遠離該處斷線受到的沖擊作用越大。

表3 不同工況下地線夾具的動力沖擊系數η

4.2.3 跨越塔構件軸力響應分析

對于大跨越輸電塔線體系，桿件的軸力起主要的控制作用。因跨越塔桿件數量過多，限于篇幅，僅對工況導線1-1 下的部分桿件進行分析。各主要桿件單元位置如圖7 所示，其中2、5、123、124、263、264、553、562 號單元為遠離跨越段的主材單元，8、11、125、126、265、266、569、578號單元為靠近跨越段的主材單元。塔身主材的動力沖擊系數η如表4 所示，由此可知，斷線對輸電塔的沖擊系數隨著塔高的升高逐漸變大，且對于塔身主材而言，遠離跨越段的主材受到斷線的動力沖擊更明顯。以橫隔材287 號和斜材329 號為例，其中橫隔材287 號位于跨越塔1標高136.7 m 的橫隔面處，如圖8 所示。二者的軸力時程如圖9和圖10所示。

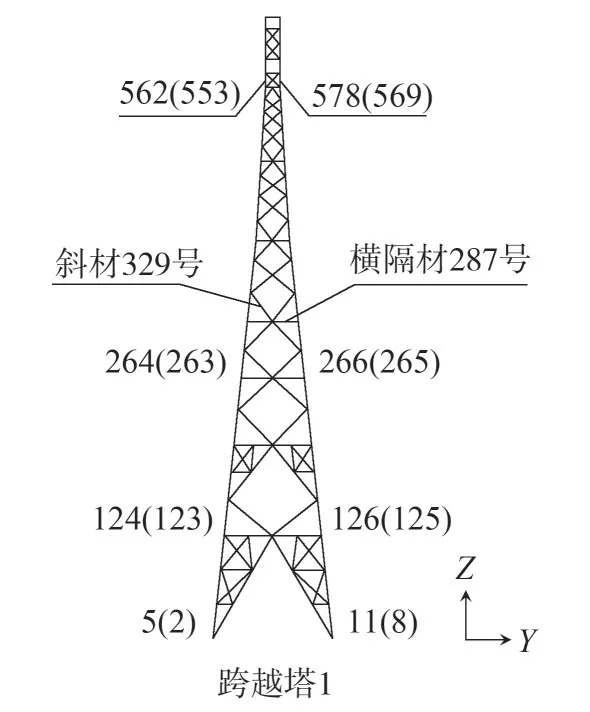
圖7 主要桿件單元位置

圖8 橫隔材287號位置

圖9 橫隔材287號軸力時程

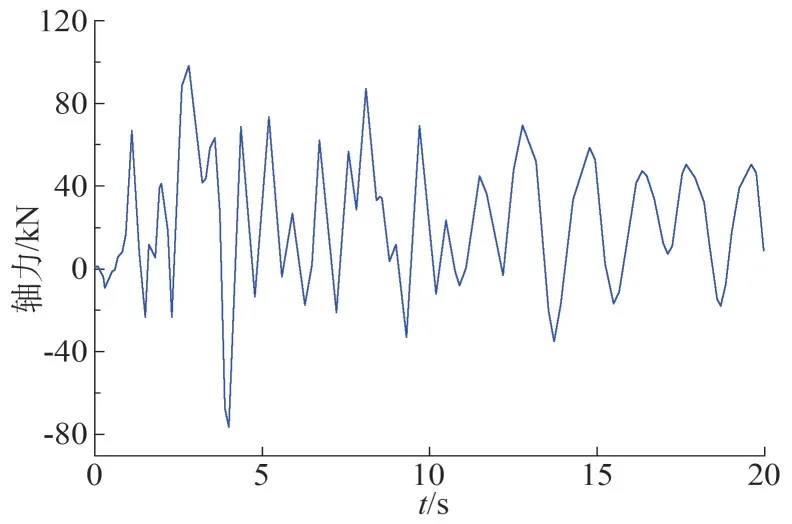
圖10 斜材329號軸力時程

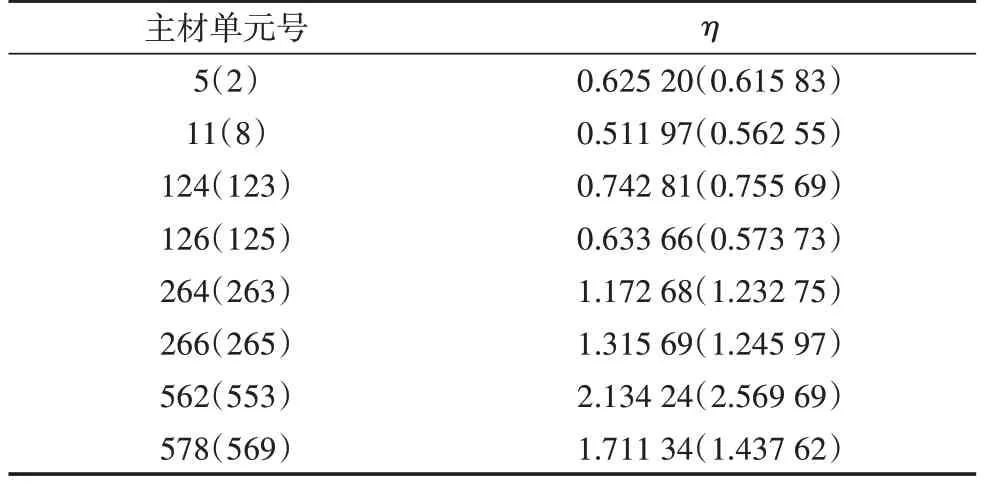
表4 塔身主材的動力沖擊系數η

可以看出橫隔材和斜材在重力荷載下基本不受力，但是在斷線下，會受到較大的沖擊作用，且會存在較大的壓力，會使斜材及橫隔材出現受壓失穩，在設計時應予以考慮，避免出現受壓失穩破壞。

5 斷線張力結果與規范方法比較

輸電線由于斷線，在斷線檔的相鄰檔輸電線具有的水平張力，即為輸電線的斷線張力［16］。經動力分析計算，可以得出最大的導線斷線張力為386 kN，最大的地線張力為79.7 kN。

根據DL/T 5485—2013《110 kV～750 kV 架空輸電線路大跨越設計技術規程》的要求，各類桿塔在斷線情況下的斷線張力的不平衡張力應按照靜態荷載考慮［17］。導線斷線張力（或分裂導線縱向不平衡張力）的取值為最大使用張力的60%，即導線的斷線張力為373 kN，地線斷線張力的取值為最大使用張力的100%，即地線的斷線張力為95.76 kN，計算可知，導線斷線動力分析計算結果要比規范的靜力計算結果大3.5%，地線斷線計算結果比規范小。

6 結語

建立大跨度輸電塔線體系的非線性有限元模型，模擬分析了導線和地線突然斷裂對輸電塔線體系的動力響應，分析表明：

1）通過斷線動力分析可以發現，若斷線根數為一根，斷線點處于跨越段的邊緣最為不利；斷線點位置靠近長耐張段的斷線響應要大于斷線點靠近短耐張段；靠近長耐張段的跨越塔（跨越塔1）響應要大于靠近段耐張段的跨越塔（跨越塔2）。

2）若斷線根數為一根，對于每個絕緣子而言，在靠近該絕緣子處斷線對該絕緣子的動力沖擊作用最大，且斷線處的絕緣子受到的動力沖擊要大于遠端的絕緣子；對于地線夾具而言，在靠近該地線夾具處斷線對該夾具的動力沖擊作用最大，且斷線處的地線夾具受到的動力沖擊要小于遠端的地線夾具。

3）大跨度輸電塔線體系的主跨過大，斷線遠端的絕緣子（地線夾具）受到掉落的導（地）線的牽拉，會使斷線遠端的絕緣子（地線夾具）軸力隨著時間逐漸變大。

4）在大跨越輸電塔線體系中，桿件的軸力起主要的控制作用，斷線對輸電塔的沖擊系數隨著塔高的升高逐漸變大。在發生斷線時，會使本身受力很小的橫隔材和斜材受到較大的壓力作用，在設計時應避免該類桿件出現受壓破壞。

5）應用動力有限元的計算結果比DL/T 5485—2013的靜力計算方法得到的導線斷線張力大3.5%，即考慮斷線的動力沖擊作用時，原設計方法會存在不安全的隱患。