合成孔徑光場成像抗混疊渲染研究

楊凱

（四川大學計算機學院，成都 610065）

0 引言

近年來，雖然微型相機（如智能手機相機）越來越受到人們的喜愛，但是對于專業攝影師而言，依然青睞于數碼單反相機生成的美學照片。由于采用了大光圈鏡頭和大型圖像傳感器，數碼單反相機能拍攝出淺景深和高信噪比的照片。然而大光圈數碼單反相機在價格昂貴制造工藝難度高，可以通過合成孔徑光場成像[1]，利用相機陣列來模擬大光圈光學設備拍攝圖像。隨著硬件設備的發展，光場成像作為計算機視覺的一個重要分支，近年來也越來越受到研究人員的關注。早在1936 年，Gershun 等人[2]就提出“光場”（Light Field）這一概念，表征光線在現實空間中的性質。到1991 年，E.Adelson 和J.Bergen[3]提出全光函數這一概念，用一個7 維函數p(x,y,z,θ,φ,λ,t)來表示空間中的幾何光線分布，其中，x，y，z表示光線的三維空間中的坐標，θ,φ表示光線的傳播方向，λ表示光的波長，t表示時間。該七維函數可以表示任意時間任意光線的傳播特性，但是難以捕獲。1996 年，Levoy[4]和Gortler[5]等人提出雙平面模型，如圖1 所示，來簡化七維全光函數，用于記錄光線在空間中的角度信息和位置信息，u，v表示相機平面，s，t表示成像平面。

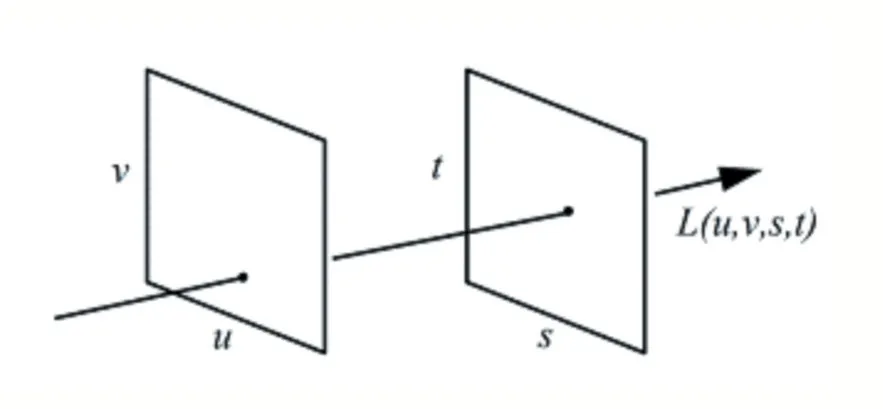
圖1 雙平面模型

在此模型的基礎上，斯坦福大學研究人員設計了光場顯微鏡[6-7]、微透鏡光場相機[8-9]、光場相機陣列[10-11]；Ng 設計研發出第一款商用級光場相機Lytro[12]，即Plenoptic1.0，利用傅立葉變換實現在頻域中快速重聚焦，能夠實現先拍照后聚焦。但是考慮到角度分辨率和空間分辨率的折中，光場相機的分辨率往往不高，一般采用超分辨技術處理最后的重聚焦圖片，例如在Lytro 相機中，CCD 的像素為11M，但實際有效分辨率只有0.7M，但最后得到的圖片分辨率為3M 左右[13]。

1 光場渲染

1.1 合成孔徑成像分析

對于傳統相機，光線通過主透鏡后匯聚在傳感器上，對于焦平面上的點將聚焦于一個像素點上，而不在焦平面上的點將形成混淆圓，相鄰像素間互相干擾，形成不清晰的像。而對于合成孔徑成像而言，通過多個相機設備模擬一個大孔徑光學設備，如圖2，各個小的相機將記錄不同角度的光線，通過計算成像，我們可以利用多個小的相機來模擬大孔徑光學設備的聚焦模糊成像效果，這個過程既是重聚焦過程。透鏡成像模型與相機陣列成像模型如圖2 所示。

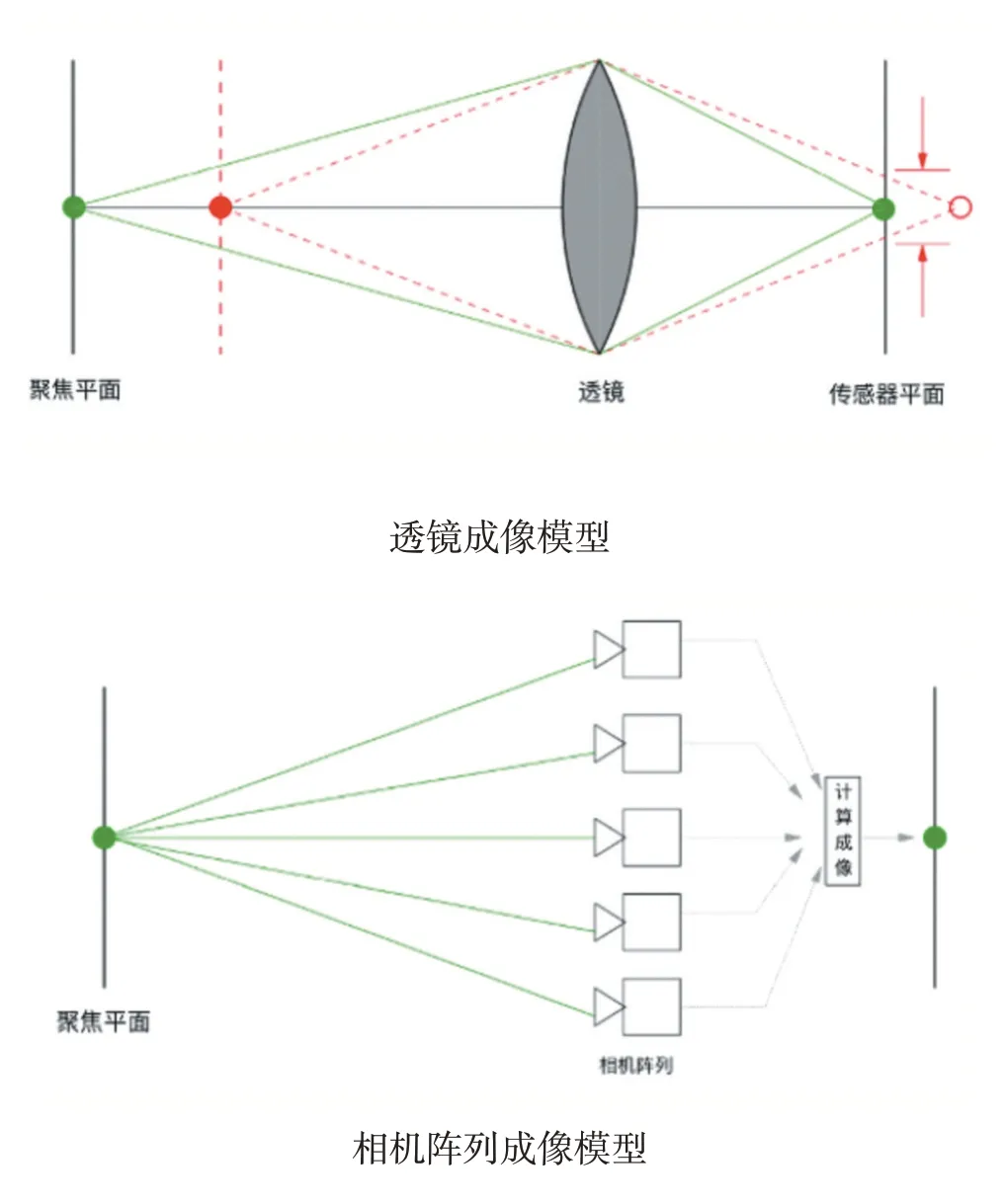
圖2

1.2 合成孔徑重聚焦理論分析

通過計算成像，我們將利用相機陣列來模擬一個大孔徑光學設備，當我們指定一個聚焦平面時，在該聚焦平面的物點將清晰成像，而不在該平面的物點將模糊。具體的做法是將每個相機得到的圖像通過反投影到聚焦平面，然后再求平均。這種反投影其實就是單應變換[14]，如圖3 所示。Π0表示指定的聚焦平面，為了得到合成孔徑光場照片，需要將相機拍攝得到的照片反投影到Π0。在Π0上的點通過反投影投后會在同一位置成像（如點P），而原本不在該平面上的點通過反投影后，將會在不同位置成像（如點Q）。

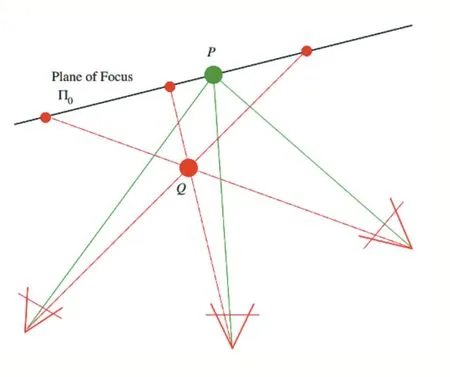
圖3 單應變換

對于給定的相機陣列有N+1 個相機，記為C0,C1,…,CN，假定C0是中心相機；Ii表示相機Ci拍攝得到的圖像，Hi表示將圖像Ii投影到聚焦平面的單應變換，得到重聚焦合成孔徑圖像公示（1）如下：

其中ISA表示重聚焦的合成孔徑圖像，表示將Ii投影到聚焦平面。圖4 表顯示了由兩個相機拍攝得到圖像，通過單應變換得到的合成孔徑圖像，聚焦平面為棋盤格所在平面。可以看出，棋盤格所在平面的物點清晰城成像，而不在聚焦平面上的點出現模糊。

圖4 通過單應實現重聚焦。頂部兩張照片是由兩個相機從不同角度拍攝而得；中間兩張對應著頂部照片的單應變換后的視圖；下左為中間兩張照片累加求平均得到，可以看出非聚焦區域出現明顯的邊緣信息重復出現；下右是通過88 個相機反投影后求平均得到，可以看出聚焦平面（棋盤格平面）清晰成像，而其他區域已經完全模糊。

圖4

2 混疊分析

上文中已經提到，合成孔徑重聚焦的過程就是各個相機圖像投影再求平均的過程，對于不在指定聚焦平面上的點，投影后將會在聚焦平面上不同位置重復出現，如圖3 中的點Q。通過相機陣列來模擬大孔徑光學設備，可以考慮為各個相機在不同的角度域上的采樣，相機陣列系統捕獲的光場信號是離散的，這種情況是由于角度欠采樣所致[15]。

如圖5 所示，V 表示相機平面，V0表示參考相機，主光軸為相機陣列虛擬合成孔徑的主光軸（即圖5 中的A）。Vx均勻分布在V0和Va間組成相機整列。T 表示圖像平面，考慮光學無窮遠處的像點P 成像在焦平面，f 表示焦距。若P 處無實際物體，則由P 后任意距離△Z的區域Dregion表面光線匯集而成。Sx表示采樣率，Sx=1/△Z，△Z表示采樣相機間距。

在該雙平面模型中，Dregion由Va和決定，當目標平面符合朗伯體假設時，對于任意相機Vx，點P 對應的成像點tx將在間采樣得到。當采樣相機個數大于間像素個數時，將不存在由角度采樣率而導致的混疊[16]，如圖5 右上所示。

3 抗混疊渲染

對于圖5 中，可以將相機陣列中的各個相機考慮為不同角度域上的采樣，稀疏排列的相機必然導致角度欠采樣，這也是合成孔徑成像重聚焦出現混疊的原因。但是現實中，出于成本和設計上的考慮，致密的相機陣列是不可取的，對于未能捕獲的光線，可以考慮采用插值計算來求得，以增加角度采樣率。如圖6 所示，對于合成的每條光線，利用附近的16 條光線插值計算求出[17]。

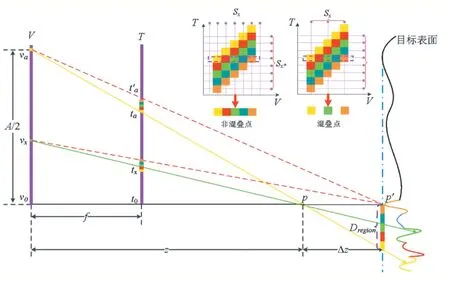
圖5 雙平面模型混疊分析

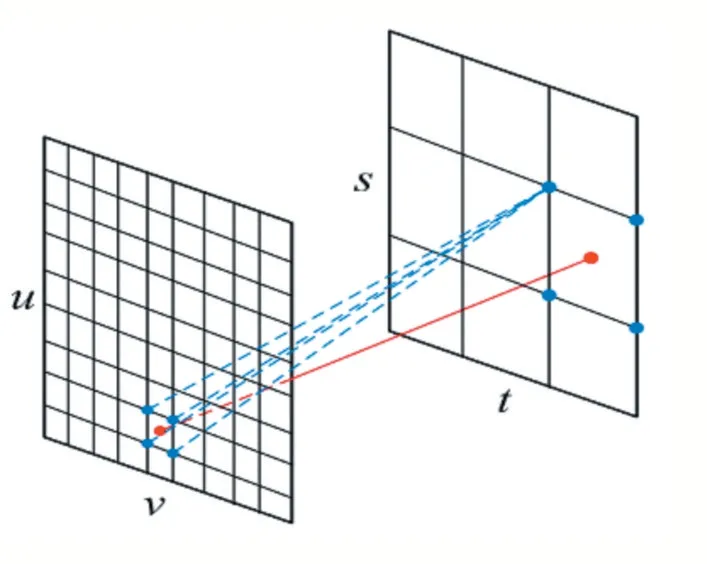
圖6 插值計算合成虛擬光線

通過插值計算合成新的視圖[18-20]，以增加角度分辨率。但是這種方法需要考慮合成新視圖所帶來的計算開銷。Chai 等人[15]和Lin 等人[21]對角度采樣率大小進行了研究，總結出相鄰視圖的最大視差必須小于一個像素，渲染出的圖像才不會出現混疊。因此通過插值計算得到新的視圖不僅將面臨計算量和新視圖數量間的折中，并且對于新視圖而言，貢獻像素的視差越小，得到的插值點越準確。

文獻[22-25]提出的方法通過將成像點進行擴散，計算得到對應的混淆圓CoC（Circles of Confusion），按照深度信息進行融合，得到最后的抗混疊渲染圖像。根據凸透鏡成像模型，如圖7 所示。未能在像平面（也就是聚焦平面）清晰成像的點p，將在圖像Ω上形成混淆圓（CoC），我們用φ(p)表示該混淆圓，

圖7 混淆圓CoC

φ(p)的直徑由如下公式（2）計算得出[25]：

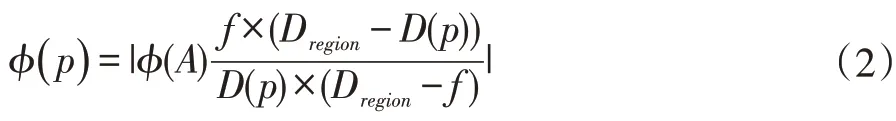
其中，D(p)表示點p 到凸透鏡的距離，f 表示凸透鏡焦距，φ(A)表示凸透鏡的直徑，F=f/φ(A)。

該類方法最后將按照深度信息進行融合，深度排序過程成本很高，也需要在計算量和渲染質量上折中。

由于混疊現象會隨著角度采樣率的增加而減弱[16]，混疊現象具有對角度采樣率敏感這一特性。肖等人[16]提出隨機變換孔徑來檢測混疊區域，利用同一個相機陣列中不同的相機組合，將得到多組光場數據。對每一組光場數據通過重聚焦得到含有混疊信息的圖像。由于混疊對角度采樣率敏感，不同角度采樣率得到的重聚焦圖像的混疊區域存在明顯差異。再檢測像素點間的變化得到混疊區域，將混疊區域通過降采樣以消除混疊，雙線性插值計算以提高分辨率，如圖8 所示。

圖8 中，第一行代表相機陣列，白色格子代表有效相機；第二行為變換孔徑成像結果，圓形表示混疊點，方框表示非混疊點；第三、四行分別表示第二行左圖、右圖中選取點的差異對比，可以看出非混疊點在不同變換孔徑中幾乎不變，而混疊點則出現明顯變換。

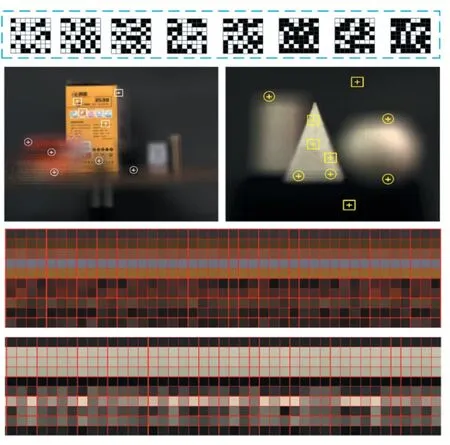
圖8

4 結語

本文對合成孔徑成像原理進行了分析，介紹了通過單應變換實現光場重聚焦，從透鏡成像模型關聯到合成孔徑成像模型，分析其中出現混疊的原因。介紹了三種抗混疊渲染方法，分別是合成新視圖、模擬成像點的混淆圓和考慮混疊區域特性。在清楚了解到各類方法的缺陷后，才能夠針對性的提出優化方案，探索時間開銷更小、成像質量更高的解決方法。