旋流預混燃燒室火焰動力學奇異譜分析研究

楊 旸,余志健

(1.中國科學院工程熱物理研究所 南京未來能源系統研究院，南京 210000；2.中國科學院工程熱物理研究所 先進燃氣輪機實驗室，北京 100190；3.中國科學院大學，北京 100190)

重型燃氣輪機主要采用貧預混燃燒技術降低氮氧化物排放。貧預混燃燒火焰傳播速度降低，同時燃燒室上取消了氣膜孔，減弱系統聲學阻尼。當熱釋放率波動與壓力波動相位差小于90°，并且注入系統的能量大于系統的耗散時，波動隨時間不斷增大，最終達到極限環狀態或過載，出現燃燒不穩定問題[1]。

在燃燒室設計階段需對火焰動力學分析以解決上述問題。目前主要有兩種方法：一是建立燃燒室閉環模型，利用快速傅里葉變化分析自激熱聲數據特性，但該方法需要燃燒系統詳細的阻抗邊界條件；二是將燃燒系統作為線性或弱線性的黑箱模型，利用脈沖響應，在開環狀態下計算火焰傳遞函數[2]。后者考慮純火焰的特性，在火焰和燃燒室設計上有更大的自由度，更適合工業應用[3]。

獲得和分析熱釋放率數據是應用上述方法的起點。由于預混燃燒中主要為大尺度湍流使火焰前緣發生褶皺，因而大渦模擬適用于預混燃燒模擬[4]。然而，由于大渦模擬時間步長小、網格尺度細，求解時間長，結果難以為設計工作提供足夠快的反饋。此外，模擬獲得的熱釋放時間序列有時間短、非平穩和趨勢被噪聲所掩蓋等特性。采用傳統的火焰傳遞函數法，計算的響應特性結果差，難以分析火焰未來趨勢，例如是否熄滅。本文將一種數據驅動算法——奇異譜分析(Singular Spectrum Analysis,SSA)應用于上述熱釋放率時間序列分析中，以進一步提取火焰動力學特性。

奇異譜分析最初由Colebrook[5]提出，用于描述海洋浮游動物濃度變化。而后Broomhead和King從一個測量的時間序列中重構了非線性動態系統的吸引子[6-7]。奇異譜分析方法對短時間、有噪聲、混沌時間序列具有良好的計算效果[8]。利用該方法的降噪能力，可有效重構自激管式燃燒室由熱聲不穩定引起的穩態和非穩態壓力時間序列[9]。與傳統方法相比，奇異譜能夠提取高度非線性的特征。采用動態模態分解分析和奇異譜分析相結合的方法，研究了高壓預混燃燒室燃燒不穩定性與火焰渦相互作用的關系。結果表明，縱向模態與軸對稱渦旋脫落有關[10]。

目前采用奇異譜方法對火焰動力學研究較為缺乏。本文對一個旋流預混燃燒室進行了大渦模擬，通過在大渦模擬中添加進口速度激勵以獲得熱釋放率響應時間序列。而后采用奇異譜分析方法重構并降解了該序列，定義了傳遞路徑響應參數(激勵與降解后熱釋放率之間的傳遞函數)，以分析火焰響應特性。此外，奇異譜模態結果還與動力學模態降解(DMD)結果比較，以形象揭示響應特性起源。本文致力于探索奇異譜方法在燃燒室設計階段對火焰動力學的分析，彌補現有方法的不足，以指導燃燒穩定的低污染燃燒室設計。

1 數值方法

1.1 大渦模擬

1.1.1 幾何及邊界條件

對旋流預混燃燒室進行大渦模擬以獲得熱釋放率時間序列。大渦模擬計算域如圖1所示。氣流方向為從左到右。圖1(b)為采用的8葉片軸向旋流器。葉片吸力面設有兩個燃料孔，壓力面設有一個燃料孔。幾何尺寸如表1所示。采用中心體半徑R1作為歸一化尺寸，摻混區長度為l，中心體末端半徑為R1_TE，擴張角為α。旋流氣流隨擴張角向燃燒室擴散時，當氣流離心力與徑向壓力梯度平衡時，根據渦破碎理論形成回流區[11]。回流區的形成通常由標準旋流數控制，旋流器速度基旋流數為0.4。邊界條件如表2所示。當前幾何條件下，當量比為0.514。

(a)模型燃燒室

表1 經R1歸一化幾何參數

表2 邊界條件

1.1.2 網格劃分和網格分辨率

網格采用star ccm生成的多面體網格，邊界層采用三層棱柱層網格。計算域為45°扇形，采用周期性邊界條件降低計算成本。燃燒室不同區域采用不同空間分辨率的網格尺寸。旋流器、摻混區、燃料孔及燃燒室上游采用更小的網格尺寸以捕捉流動和火焰細節。整體網格劃分和局部位置網格如圖2所示，總網格數為460.5萬。

圖2 全局及局部網格劃分

Fluent在大渦模擬求解中采用隱式求解器，無網格無關性檢驗，因為無限減小網格尺寸將導致求解趨向DNS。本文采用基于能量指數法的后檢驗來判斷網格在LES計算中是否足夠好。即當求解的湍流動能占總湍流動能85%時，認為網格求解精度達到[12]。由于應用邊界中心差分格式進行空間離散，因此總湍流動能中忽略由數值格式引起的能量耗散。中心平面后估計指數M分布云圖如圖3所示，可以看出大部分區域能量占比都大于85%,由于本研究集中在火焰區，出口小部分區域解析度不夠也可滿足本文研究目的。

圖3 中心平面后估計指數M分布云圖

1.1.3 數值方法

生成的網格導入ANSYS fluent 18.0進行數值計算。大渦模擬采用WALES亞網格尺寸模型[13]，燃料和空氣進口無湍流波動設置。瞬態求解采用二階差分格式。CFL數在全域內保證小于1。采用部分預混燃燒模型，該模型通過求解進程變量的平均輸運方程模擬預混燃燒反應。控制方程如下所示：

(1)

(2)

ut=Au′Da1/4

(3)

甲烷燃燒采用GRI 3.0反應機理[15]，比熱容與溫度的關系采用分段多項式模型。模擬中采用絕熱邊界條件。

1.2 火焰傳遞函數和傳遞路徑響應

(4)

傳遞函數計算步驟如下：1)計算輸入信號的自功率譜；2)計算輸入和輸出的互功率譜；3)在拉普拉斯域上獲得輸入與輸出的幅值和相位值。

1.3 奇異譜分析

奇異譜分析是處理平穩或非平穩時間序列的一種無模型方法。時間序列在無先驗假設前提下，可分解為趨勢、周期及噪聲等可解釋分量[21]。首先將燃燒室大渦模擬獲得的熱釋放率時間序列

(6)

(7)

窗長度為L(L需小于n/2)，奇異譜分析算法步驟如下[21-22]：

(1)嵌入

首先獲得軌跡矩陣Y(Hankel矩陣)。

(8)

窗長度L越大，原時間序列信息損失越大；L越小，計算量越大，存儲所需內存越大。

(2)奇異值分解

對矩陣Y進行奇異值分解，Y=UΣVT。其中UL×L,V(n-L+1)×(n-L+1)為左右奇異向量，ΣL×(n-L+1)為對角線矩陣，其中特征值λi按照降序排列。根據譜分析理論，矩陣Y可用前d階模態重構，如公式(9)所示。

(9)

(3)重構

(4)篩選

由于奇異值分解的特征值已經以遞減的方式排序，因此可選擇前k個模態進行分析。引入回歸模型中協方差R2值，R2越接近1，表明自變量對因變量的解釋越有效。

2 結果與分析

2.1 火焰結構和火焰傳遞函數

中心平面時均和均方根(RMS)進程變量(Progress Variance，PV)分布云圖如圖4所示。從時均云圖可看出，中心回流區PV值為1，角回流區PV值小于0.8，在火焰內層下游，PV也小于0.8，火焰面有效形成。進程變量RMS云圖表明火焰內外層之間有強烈的混合，而中心回流區與火焰內層混合作用弱。

圖4 中心平面時均(上)和RMS(下)進程變量(PV)云圖

激勵響應大渦模擬過程，熱釋放率采樣頻率為10 000 Hz。圖5為從大渦模擬中采集的激勵后熱釋放率時間序列，可以看出熱釋放率呈下降趨勢。Kwiatkowski-Phillips-Schmidt-Shin (KPSS)測試表明該序列趨勢上是非平穩的，但序列的一階導數是平穩的，因而可進行奇異譜分析。圖6為計算的火焰傳遞函數幅值和相位。傳遞函數幅值在零頻率附近有較高的幅值，較高的幅值掩蓋了其它頻率帶的響應信息，因而火焰準確的響應頻率信息難以從火焰傳遞函數中獲得。需發展新方法如奇異譜分析進一步揭示熱釋放率內在響應信息，以指導燃燒室設計。

圖5 激勵后熱釋放率時間序列

圖6 火焰傳遞函數

2.2 熱釋放率時間序列奇異譜重構

窗長度L選為1 200，圖7為各階重構矩陣對軌跡矩陣的單獨和累計能量占比。可以看出采用前20階模態的重構矩陣累計能量占原矩陣能量的80%以上。第7階之后的單獨模態能量占比都保持較低水平。采用前20階模態重構后，累積協方差達到0.9以上，表明前20階模態重構原始熱釋放率時間序列有效。

圖7 各階重構矩陣Y占軌跡矩陣的單獨和累計能量

圖8為前k(k=10,20)階奇異譜模態重構后的熱釋放率時間序列與原始時間序列對比。可以看出采用前20階奇異譜模態重構的時間序列可有效的跟蹤原始時間序列，并可準確捕捉熱釋放率波動特性。后續主要以前20階奇異譜模態進行分析。

圖8 采用前k階奇異譜模態重構后的熱釋放率時間序列和原始序列對比

2.3 奇異譜模態和傳遞路徑響應

圖9為1、4、9及12階熱釋放率奇異譜模態時間序列。圖10至圖14為熱釋放率按響應特性分類的奇異譜模態傳遞路徑函數幅值。從熱釋放率奇異譜模態幅值可以看出，模態可以劃分為趨勢模態和對特定頻率的四種響應模態。趨勢模態反映熱釋放率隨時間變化的總體趨勢，響應模態反映熱釋放率的動態響應特性。響應特性分為32 Hz、56 Hz和112 Hz、200 Hz以及128～136 Hz。圖9為第一、三和四種響應類型中的首階模態和第二種響應類型的第二階模態(首階和第二階模態能量占比較大)的時間序列。

(a)1階

1階和2階模態反映熱釋放率的趨勢特性。圖10為1階和2階模態傳遞路徑響應幅值。從圖9(a)可以看出，1階模態的振幅隨時間不斷衰減，在0.15 s后達到低值并保持。傳遞路徑響應幅值曲線可以看出在零頻率處保持較高增益，表明熱釋放率時間序列趨勢演變是低頻的。

圖10 1階和2階趨勢模態火焰傳遞路徑響應

3、4、5和6階奇異譜模態對32 Hz頻率有響應。圖11為3、4、5和6階模態傳遞路徑響應幅值。從圖9(b)，可以看出4階模態的時間序列呈波動狀，振幅隨時間不斷增大。從頻譜特性看出，該部分各模態的特征頻率在30 Hz左右，與響應特性保持一致。

圖11 32 Hz響應模態(3、4、5和6階)傳遞路徑響應

9、10、11、18和19階模態同時有56 Hz和112 Hz響應特性。圖12為上述各階模態傳遞路徑響應幅值。從圖9(c)所示，9階模態時域上也為波動狀，頻譜上主頻在110 Hz左右。傳遞路徑響應幅值有56 Hz和112 Hz兩個主頻。

圖12 56 Hz和112 Hz響應模態(9、10、11、18和19階)傳遞路徑響應

12和13階熱釋放率模態對200 Hz有響應特性。圖13為12和13階模態傳遞路徑響應幅值。從圖9(d)所示，12階模態時域上振幅不斷增大，到最大值后衰減。傳遞路徑響應曲線表明主頻有200 Hz。

圖13 200 Hz響應模態(12和13階)傳遞路徑響應

16階模態對頻率帶128～136 Hz有響應。圖14為16階模態傳遞路徑響應幅值，響應峰帶寬較長。如圖6所示，采用傳統的火焰傳遞函數方法，難以解析出設計階段大渦模擬獲得的短時、非穩態和含噪聲的非穩態熱釋放率數據響應特性。采用奇異譜分析處理這類數據，通過各階模態傳遞路徑響應特性，可有效分辨出熱釋放率的響應特性。

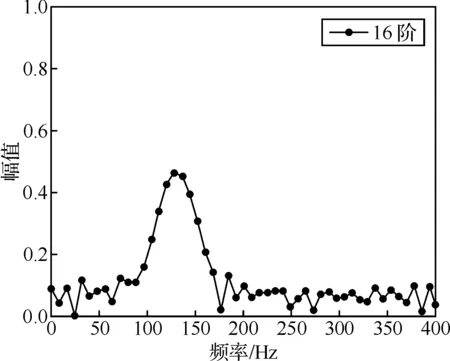
圖14 128～136 Hz響應模態(16階)傳遞路徑響應

進一步對奇異譜各階模態的時間序列進行分析，圖15為各響應頻率代表性模態時間序列遞歸分析圖。可以看出對于1階和2階的趨勢模態(無特定響應頻率)，模態遞歸圖為黑白圖，無明顯特征規律。對于具有32 Hz響應特性的3階和4階模態，模態遞歸圖為黑白相間的棋盤狀，且某一區域該特征極為明顯。對于具有200 Hz響應特性的12和13階模態，時間序列模態遞歸圖也呈棋盤狀，且棋盤尺寸更為密集，代表響應頻率越高。

圖15 各響應頻率代表性模態時間序列遞歸圖

表3為動力學模態降解(DMD)處理該熱釋放率時間序列獲得的各階模態特征頻率和增長率值。與奇異譜分析方法獲得的模態特征頻率對比，可以發現奇異譜中的32 Hz、112 Hz和200 Hz左右的響應頻率也可被DMD方法的11階、13階和18階模態捕獲。圖16為動力學模態降解法獲得的18階模態(對應31 Hz響應)進程變量的分布云圖，可以看出該模態下，火焰內外層有剪切運動，角回流區和中心回流區有混合作用。

表3 動力學模態降解法獲得的各階模態頻率及增長率

圖16 動力學模態降解法獲得的18階模態(對應31 Hz響應)

3 結論

(1)燃燒室設計階段，對于某些工況下采用大渦模擬獲得的短時、非穩態和含噪聲的熱釋放率時間序列，采用傳統火焰傳遞函數法獲得的頻率響應信息易被低頻高幅值段掩蓋。

(2)對熱釋放率時間序列采用奇異譜分析方法處理，重構后熱釋放率時間序列可有效吻合原始時間序列。

(3)奇異譜分析方法獲得的各階模態火焰傳遞路徑響應參數表明，模態可分為趨勢模態和響應模態；該火焰有4種典型的頻率響應特性，分別為32 Hz、56 Hz和112 Hz、200 Hz以及128～136 Hz響應，揭示了火焰內在頻率響應特性。

(4)動力學模態降解法捕獲的31 Hz、98 Hz和187 Hz頻率與奇異譜模態獲得的四種響應特性基本吻合。31 Hz下DMD模態形狀可以看出火焰內外層有剪切運動，回流區有混合作用。