不同雷諾數下圓柱結構渦激振動的數值模擬

任彤煜，王秋波，張筱璐,2，齊巍

1.北京工業大學 機械工程與應用電子技術學院，北京 100022

2.北京工業大學 汽車結構部件先進制造技術教育部工程研究中心，北京 100124

3.中國汽車技術研究中心有限公司，天津 300300

流致振動廣泛存在于工程實踐中，交替脫落的漩渦會導致傳熱管劇烈振動，并引起失效、斷裂等安全事故。工業應用中的傳熱管多為圓柱體結構，在順流向和橫流向均易產生振動[1-2]，Oviedo-Tolentino 等[3]在低雷諾數的水洞中對質量阻尼系數為0.126、底部固定的直圓柱結構開展流致振動試驗，發現在不同雷諾數時，圓柱體的振動響應由不同的頻率決定。徐萬海等[4]在雷諾數為800～16 000 時研究直圓柱結構順流向渦激振動響應特性，發現了順流向響應頻率一般“鎖定”在固有頻率附近的現象。Williamson 等[5]在水流條件下對僅能在橫流向進行振動的直圓柱管進行研究，發現低質量比直圓柱管的振幅隨雷諾數的增大而不再均勻變化，出現分支現象。同時，部分學者也針對彎圓柱管結構開展流致振動特性研究[6-9]，Zhu 等[9]在雷諾數為165～1 129 時對質量阻尼比為0.11 的彎圓柱管開展實驗研究，發現彎圓柱管不同位置處的振動頻率不同，表現出多模態響應且橫流向和順流向的最高模態響應不同。目前，單圓柱體實驗研究中與傳熱管相關的研究較少，其試驗成本較高，試驗周期較長。因此，學者針對不同工況下圓柱結構振動特性的數值模擬也開展了相關研究，Breuer 等[10]在雷諾數為140 000的條件下，對直圓柱結構進行三維數值模擬，結果表明采用數值模擬方法獲得的圓柱繞流三維數值計算和實驗結果吻合較好。Miliou 等[11]對雷諾數分別為100 和500 的彎曲圓柱體進行研究，發現“凸型結構”的背面具有交錯排列的渦旋的反對稱尾波，而“凹形結構”沒有漩渦脫落特征。Yamamoto 等[12]采用離散渦方法對柔性立管的渦激振動現象進行數值研究，將數值結果與實驗結果進行了對比，數值模擬出來的振幅值比實驗結果略小，尾流模態與實驗結果保持一致。上述研究分別針對直圓柱和彎圓柱開展，而較少通過數值模擬分析的方法在相同雷諾數下對直、彎圓柱數值模擬分析的振幅、振動頻率開展對比研究。

本文分別對直圓柱管模型和彎圓柱管模型進行干模態、濕模態振動分析，并采用SSTk-ω湍流模型對雷諾數為7 500～42 000 的直圓柱管和彎圓柱管進行流固耦合分析，獲取模型在不同流速下順流向與橫流向的振幅特性和頻譜特性，并與試驗數據進行對比，為研究圓柱管渦激振動特性提供參考。

1 數值模擬方法

1.1 幾何模型建立

在ANSYS Workbench 中建立直圓柱管模型及其流體域，模型由外徑為17 mm、內徑為12 mm、長度540 mm、質量比為3.94、材料為結構鋼的直圓柱管和尺寸為200 mm×100 mm×550 mm、包裹直圓柱管的水域組成(圖1(a))。定義直圓柱管結構模型的一端為固定約束；流體域為聲場，聲速為1 500 m/s；求解算法為對稱耦合；重力加速度為9.8 m/s2；直圓柱管內腔由空氣填充，外壁與水的接觸面為流固耦合面；將直圓柱管設置在水域的中心位置。按相同方法建立彎圓柱管有限元模型，模型由外徑為17 mm、內徑為12 mm、彎曲半徑為659 mm、弧長為540 mm、質量比為3.94 的彎圓柱管模型以及底面尺寸為200 mm ×100 mm、側面圓弧彎曲半徑分別為709、609 mm 的水域組成(圖1(b))。彎圓柱管軸線距離入口段100 mm，距離兩側壁面50 mm，同時彎圓柱上表面距離流場上表面10 mm，對彎圓柱管重復直圓柱管的設置。

圖1 圓柱管有限元模型參數設置

1.2 網格無關性驗證

為檢驗網格劃分對當前模型分析結果的影響，對直圓柱管和彎圓柱管有限元模型進行結構化網格劃分，并對3 種不同數量的網格進行無關性驗證，結果如表1 所示。

表1 結果顯示，當直圓柱管的網格數量從15 202增加到26 911 時，直圓柱管前三階振動頻率的變化百分比分別為1.62%、0.73%和0.23%；當網格數量從26 911 增加到57 473 時，直圓柱管前三階振動頻率的變化百分比分別為0.05%、0.004%和0.30%。當彎圓柱管的網格數量從15 441 增加到25 446 時，彎圓柱管前三階振動頻率的變化百分比分別為0.15%、0.03%和0.14%；當網格數量從25 446 增加到56 934 時，彎圓柱管前三階振動頻率的變化百分比分別為0.05%、0.06%和0.06%。通過分別對比直圓柱管模型和彎圓柱管模型3 種不同疏密網格條件下的前三階振動頻率可知，網格數量對濕模態計算結果的影響較小。綜合考慮計算時間和計算精度，直圓柱管采用序號1 的網格劃分方式，彎圓柱管采用序號4 的網格劃分方式。

表1 網格無關性分析

1.3 流固耦合模擬分析

為分析直圓柱管和彎圓柱管在流速0.4 6～2.5 m/s 的振幅和振動頻率，對圖1 中的圓柱管有限元模型進行流固耦合模擬，將圓柱管渦激振動簡化為橫流向和順流向圓柱管自由振動。所采用的控制方程為

式中：u、v分別為順流向速度、橫流向速度，ρ為流體密度，μ為流體黏度，p為壓力，m為圓柱管質量，x、y分別為t時刻圓柱管順流向位移、橫流向位移，Fx(t)、Fy(t)分別為圓柱管順流向流體力、橫流向流體力。

本文使用ANSYS 的Fluent 模塊、Transient Structure 模塊以及System Coupling 模塊，對直圓柱管進行流固耦合模擬。首先對直圓柱管進行網格劃分，在直圓柱管的近場區域采用結構化網格，遠場區域采用非結構化網格，邊界層劃分為10 層。在Fluent 中設置流場參數，選取SSTk-ω湍流模型，流體域采用速度入口，無滑移壁面，進口流速為0.46～2.5 m/s(雷諾數為7 500～42 000)，出口壓力為0，設置時間步長為0.04 s，計算時間為2 s。對彎圓柱管重復上述操作，進行流固耦合分析。

2 試驗測試方法

在如圖2 所示的試驗裝置中對直圓柱管開展試驗測試。直圓柱管試驗模型的物理參數、在試驗段中的安裝位置與直圓柱管有限元模型保持一致，保持直圓柱管一端固定、一端自由振動。在試驗開始前，啟動離心泵，檢查試驗裝置的封閉性并排出試驗裝置中的空氣。試驗的初始流速為0.46 m/s，采用1 個三軸加速度傳感器測量直圓柱管自由端加速度信號，并當電磁流量計讀數穩定30 s 后，用LMS 數采系統采集加速度傳感器數據，時長200 s，之后按0.14 m/s 的流速等距間隔逐漸增加到2.5 m/s，共在16 組試驗流速下采集數據。由于加速度傳感器安裝在直圓柱管結構自由端的內壁位置，傳感器的安裝和連接線不會改變圓柱管模型本身的物理參數，也不會受到外界的電磁干擾。直圓柱管測試完成后，選取與彎圓柱管有限元模型參數相同的彎圓柱管試驗模型，在上述試驗工況下對彎圓柱管開展試驗測試。

圖2 試驗裝置示意

3 結果分析與討論

3.1 模態分析

為驗證數值模擬分析的合理性，分別開展干模態和濕模態試驗獲取直圓柱管和彎圓柱管前三階空氣環境中的固有頻率值、靜水環境中的固有頻率值。對比直圓柱管數值模擬與試驗測試結果可知，空氣環境中的前三階固有頻率偏差分別為3.3%、4.1%和1.6%，靜水環境中的前三階固有頻率偏差分別為3.5%、1.3%和3.3%；對比彎圓柱管數值模擬結果與試驗結果可知，空氣環境中的前三階固有頻率偏差分別為1.7%、1.1%和1.3%，靜水環境中的前三階固有頻率偏差分別為1.6%、3.0%和2.9%。2 種圓柱管數字模擬結果和試驗結果的誤差在5%以內，結果如表2 所示。

表2 空氣環境與靜水環境中直圓柱管和彎圓柱管的前三階固有頻率

3.2 不同流速下圓柱管振幅的數值模擬與試驗結果對比

圖3 為直圓柱管和彎圓柱管在不同流速下橫流向加速度幅值的數值模擬和試驗結果。

圖3 直圓柱管、彎圓柱管橫流向振幅隨流速變化關系

由圖3 可知：對于直圓柱管，在流速為0.46～1.91 m/s 時，直圓柱管橫流向振幅隨流速的增大而緩慢增大；而當流速為1.91～2.5 m/s 時，直圓柱管橫流向振幅急劇增大。對于彎圓柱管，當流速為0.46～2.19 m/s 時，彎圓柱管橫流向振幅隨流速的增大而緩慢增大；而在流速為2.19～2.5 m/s 時，彎圓柱管橫流向振幅急劇增大。數值模擬的2 種圓柱管橫流向振幅響應只存在“初始分支”。振幅響應未出現從“初始分支”到“上分支”的變化，未發生“鎖頻現象”，數值模擬結果與試驗結果保持一致。用F 檢驗法，取置信度為95%，分析整個流速范圍內數值模擬和試驗結果的顯著性差異。統計量F=0.16，對應的臨界值為4.15，由于統計量小于臨界值，2 組數據沒有顯著差異；用相同的方法分析彎圓柱管數值模擬和試驗數據的顯著性差異，統計量F=0.27，對應的臨界值為4.17，由于統計量小于臨界值，2 組數據沒有顯著差異。因此直圓柱管和彎圓柱管有限元模型可用于模擬流速為0.46～2.5 m/s 時直圓柱管和彎圓柱管的橫流向振幅。

圖4 為數值模擬和試驗獲得的不同流速下直圓柱管和彎圓柱管順流向振幅。

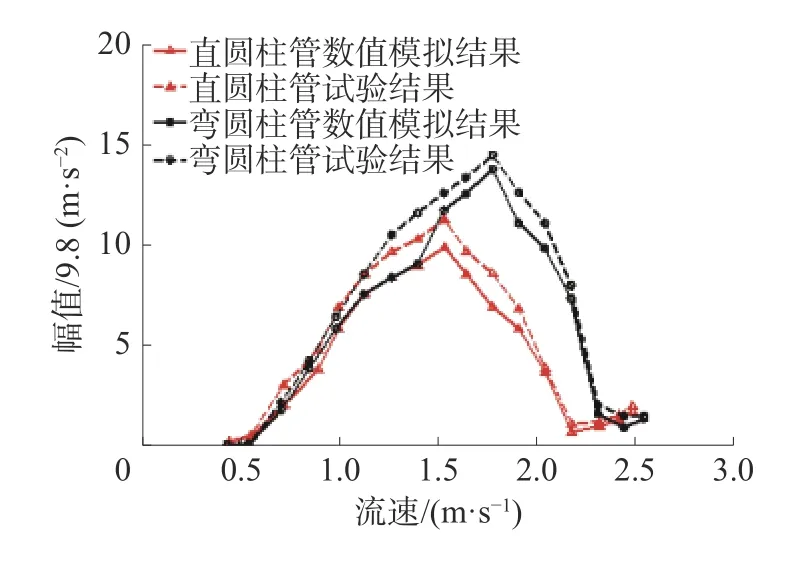
圖4 直圓柱管、彎圓柱管順流向振幅隨流速變化關系

直圓柱管振幅在流速為0.46～1.54 m/s 時逐漸增大，而在流速為1.54～2.19 m/s 時逐漸減小，在流速為2.19～2.5 m/s 時緩慢增大；彎圓柱管振幅在流速為0.46～1.78 m/s 時逐漸增大，在流速為1.78～2.42 m/s 時逐漸減小，在流速為2.42～2.5 m/s 時緩慢增大。直圓柱管和彎圓柱管的順流向振幅均隨流速的增大而先增大、后減小、之后略有增大，數值模擬的順流向振幅隨流速變化趨勢與試驗結果保持一致。用F 檢驗法，取置信度為95%，分析整個流速范圍內數值模擬和試驗結果的顯著性差異，統計量F=0.44，對應的臨界值為4.17，統計量小于臨界值；用上述相同方法分析彎圓柱管數值模擬和試驗數據的顯著性差異，統計量F=0.27，對應的臨界值為4.17，統計量小于臨界值。直圓柱管和彎圓柱管有限元模型可用于預測直圓柱管和彎圓柱管在流速為0.46～2.5 m/s 時的順流向振幅。

3.3 不同流速下圓柱管頻譜的數值模擬與試驗結果對比

為進一步驗證直圓柱管和彎圓柱管有限元模型的合理性，分析漩渦脫落開始階段2 種圓柱管橫流向頻譜的數值模擬結果和試驗結果。當流速為1.91 m/s 時，直圓柱管和彎圓柱管在20 Hz左右出現振動峰值，同時受到順流向振動頻率的影響，分別在36、38 Hz 處存在較小峰值，如圖5(a)所示；當流速為2.05 m/s 時，直圓柱管和彎圓柱管頻率集中在1/2 倍固有頻率、漩渦脫落頻率和固有頻率附近，如圖5(b)所示；當流速為2.19 m/s時，直圓柱管和彎圓柱管的頻率值保持不變，如圖5(c)所示；當流速為2.33 m/s 時，直圓柱管和彎圓柱管主要受漩渦脫落頻率影響，如圖5(d)所示。數值模擬的振幅與試驗結果吻合較好，振動頻率的數值模擬與試驗結果偏差較小，偏差為0.8 Hz。

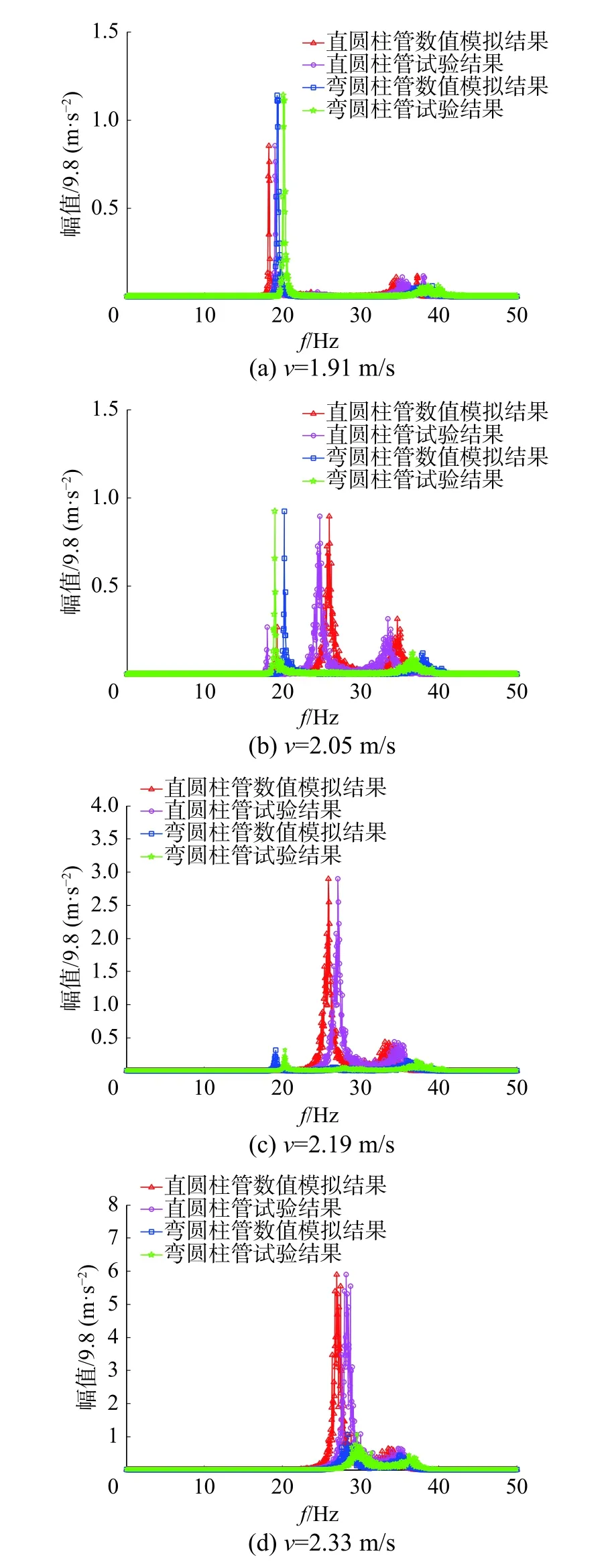
圖5 不同流速下直圓柱管、彎圓柱管橫流向頻譜

圖6 為2 種圓柱管在圖5 相同流速條件下順流向頻譜的數值模擬和試驗結果：2 種圓柱管在相同工況下數值模擬的頻譜與試驗結果近似程度較高，由數值模擬獲得的頻譜圖中的頻率比實驗獲得的頻譜圖中的頻率小1 Hz 左右。當流速為1.91～2.05 m/s 時，直圓柱管頻率約為38 Hz，數值模擬結果與試驗結果基本吻合，偏差在0.8 Hz左右；彎圓柱管振動頻率約為40 Hz，數值模擬結果與試驗結果基本吻合，偏差在0.7 Hz 左右。

圖6 不同流速下直圓柱管、彎圓柱管順流向頻譜

4 結論

本文采用ANSYS 軟件對直圓柱管和彎圓柱管有限元模型進行流固耦合分析，分析曲率平面對單圓柱管振動的影響，并與試驗數據對比分析，得出如下結論。

1)雷諾數為7 500～42 000 的直圓柱管和彎圓柱管橫流向振幅隨流速的增大而增大，出現初始分支，這說明曲率平面未影響圓柱管橫流向振幅隨流速的變化規律。

2)在上述亞臨界雷諾數范圍內，直圓柱管和彎圓柱管的順流向振幅均先增大，后減小。圓柱管順流向振幅隨流速變化規律不受曲率平面影響。

3)在漩渦脫落開始階段，直圓柱管和彎圓柱管的漩渦脫落頻率隨流速的增大而增大，且相同雷諾數條件下，彎圓柱管漩渦脫落頻率較大，這可能是因為曲率平面影響圓柱管的漩渦脫落狀態。

4)直圓柱管和彎圓柱管順流向頻率在漩渦脫落初始階段基本保持不變，分別為38、40 Hz。

本文的研究成果可為傳熱管的設計及優化提供借鑒。為證明曲率平面對圓柱管振動影響的適用性，可對不同縱橫比、不同彎曲半徑的彎圓柱管結構開展研究。由于多圓柱間存在互擾作用，可以進一步研究曲率平面對多圓柱管結構振動的影響。