基于IMMPF 對異型空間的室內定位算法研究

席志紅，王琦

哈爾濱工程大學 信息與通信工程學院，黑龍江 哈爾濱 150001

進入21 世紀，基于位置服務(location based services,LBS)在諸多領域的需求日益增大。基于位置服務是指由移動通信網絡終端、無線局域網等無線通信網絡技術進行定位，進而獲取待測目標物體的位置信息，所獲取的定位信息被用戶應用于實現各種位置相關的業務服務。目前從定位場景進行劃分可分為室外定位與室內定位。對于室外定位，全球衛星導航系統[1]完全可以提供較高精度定位結果，當前具有代表性的主要有中國北斗衛星定位系統、歐盟的伽利略衛星導航系統、美國的全球定位系統以及俄羅斯的全球衛星導航系等[2-5]幾大定位系統。室外定位系統主要依靠衛星以及雷達等硬件設備實現，采用以多衛星聯合的方式實現戶外定位。但將其應用于室內定位就會出現誤差較大以及不適用于復雜室內空間環境等問題，主要原因是室內定位時，由于建筑物墻體以及室內環境中各類物體等遮擋的影響，衛星信號的衰落非常明顯，使得定位的誤差巨大而無法達到較好的定位效果。隨著人們在醫院、大型商場以及博物館等環境中的活動日益增多，人們對于復雜空間的室內定位需求越來越大。目前的室內定位技術主要有WIFI 定位、藍牙定位和光纖定位等[6-8]。

在許多大型商場以及醫院中，墻體以及其他物體的遮擋對WIFI 信號有較大的影響，定位目標與無線訪問節點(access point,AP)之間存在視距(LOS)[9]與非視距(NLOS)[10]等交替變換情況，所以，如何保證對異型空間的室內定位的高精度是如今亟需解決的問題。考慮到環境系統的非線性特點，擬采取PF[11]來做數據融合。但是由于粒子濾波高效率定位僅局限于在高度非線性環境中，對于定位技術的融合無法解決異型空間下的NLOS 干擾問題。本文采用基于IMM[12]的算法，可以有機地將兩者信道模型兼用，實現對此類環境中運動物體進行高精度定位。

本文采用交互多模型與粒子濾波相結合的技術，并針對實際的定位環境，提出改進的IMMPF的室內定位算法：首先對運動目標與噪聲進行建模，在狀態模型更新時利用粒子濾波對于狀態以及NLOS/LOS 狀態參數進行融合；同時對于異型復雜環境中無法表示真實的概率密度函數分布，通過改變粒子權重值向似然函數峰值靠近，有效地增大粒子的有效性，使得采樣粒子更接近真實狀態，進而可以有效避免NLOS 對于定位影響。

1 基于WIFI 指紋的定位算法

1.1 基于位置指紋定位原理

在室內某處的WIFI 信號，在無外加干擾情況下強度穩定不變。依據這條特性完成建立相應的指紋庫。采用指紋庫的方式進行定位研究，可以有效避免定位時因為環境原因所產生的多徑效應干擾，有效抑制多徑效應以及陰影衰落對定位結果帶來的影響。定位可以劃分為離線指紋采集和在線匹配定位2 個階段。離線階段主要完成對室內定位空間各處位置信息進行WIFI指紋的采集，對于當前位置WIFI 接收信號強度指示(received signal strength indication，RSSI)進行分析提取，作為當前位置的指紋信息存儲于指紋庫；在線階段主要完成對于實時接收空間的AP 所發射的WIFI 信息強度，通過分析WIFI 信息中所包含的信息特征與指紋庫進行比對匹配，進而得到定位信息。圖1 為基于位置指紋的模型圖。

圖1 基于位置指紋模型

1.2 WIFI 指紋庫的建立

本文實驗地點為某教學樓的四樓走廊，實驗區域內WIFI 信號全覆蓋，采用華為手機以及傳感器進行WIFI 信息的采集，在空間內均勻布置6 個AP 發送設備。AP 的服務集標識(service set identifier，SSID)用于區分同一區域所接受的WIFI 信號強度。實驗環境被分割為1 m×1 m 的網格結構，對在進行WIFI 信息的采集過程中的人員走動不受限制，同時充分考慮在教學樓內進行實驗的人員日常行動習慣以及空氣濕度對于WIFI信息采集的影響，分多個時段進行WIFI 信息采集。

在室內定位空間內的同一位置測量的WIFI信號強度會因為室內空間的干擾，在指紋庫里產生不穩定的波動數據值，這些不穩定值對室內定位的準確性以及誤差均存在著干擾。本文通過采用高斯分布模型進行數據篩選，從采集的數據中篩選出高準確率的數據，對所選擇數據進行求取幾何平均數即可得到高斯濾波結果。

RSSI 服從(0μ2)分布，其概率密度公式如下：

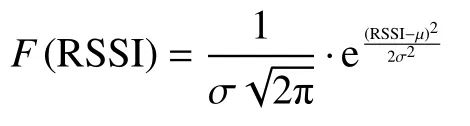
式中：μ為均值，σ2為方差。

針對因為噪聲等因素干擾而產生的RSSI值波動，本文對于傳統的高斯濾波進行改進，具體步驟如下。

1)輸入采集樣本值。為了避免噪聲的干擾，在進行信息采集時應當進行多次采集。

2)高斯濾波。對于第一部分的樣本值引入高斯模型濾波處理，選取概率空間為90%以內。

3)小概率樣本值處理。通過高斯濾波技術可以有效地對小概率空間樣本值進行剔除，設置小概率空間集合為W，集合空間內的樣本數為k：

對于集合空間內的樣本值進行賦值：

式中 RSSIj為集合W中的數據，j=1,2,···,k。

4)輸出結果降噪。通過濾波技術將小概率空間的數據賦值后，再通過樣本選取標準將其匯入大概率空間的樣本數據中，最終保存在離線指紋庫中。

2 IMMPF 的定位算法

2.1 系統模型

為了方便我們研究在NLOS 環境中的定位問題，設定系統的狀態方程為

式中：X為狀態向量；A為轉換矩陣，其維數為n×n階；B為轉換矩陣；ω為系統噪聲輸入。

當測量值為Z時，則測量值和狀態值之間的關系為

式中：H為系統的轉換矩陣，其維數為m×n階；vk為系統的測量噪聲。

設V(k)為觀測噪聲量，對LOS 環境以及NLOS 環境下的噪聲量進行分解，LOS 環境下服從分布，NLOS 環境下服從?d為距離差變量，其數值大于等于0。則概率密度函數可表示為

考慮到多信道模型，本文在其中加入了信道狀態量

式中：xi(k)為運動目標參數向量；xLOS(k)和xNLOS(k)分別為對應情況的距離差變量向量，有

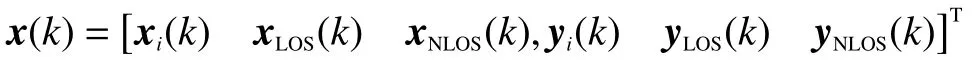
通過經驗可知，在實際的定位過程中，NLOS環境的量化噪聲遠遠高于LOS 環境。所以，對于定位參數的精準設定難以實現。

分別對NLOS 和LOS 環境測量噪聲概率分布均值進行建模

2.2 IMMPF 算法

由于實際的復雜空間室內定位運動模式的不確定性，室內運動目標運動狀態難以確定。傳統的單模型算法在復雜空間的室內定位中無法對定位目標進行實時性跟蹤，導致在空間進行跟蹤定位時精度較差，難以實現工程應用。多模型(multiple model，MM)算法其核心思想是對室內空間運動目標進行多點運動模式跟蹤定位。在多模型算法中，以交互多模型算法為主流。交互多模型算法是具有較高實用價值的代表性算法，其在多模型的基礎上，對模型數據集里的模型進行加權，通過設定似然函數和Markov 模型轉移并結合各個模型進行運算。

交互多模型算法主要分為輸入交互、狀態濾波、模型概率更新和狀態輸出這4 個模塊。交互多模型算法通過采用運動模型集對物體運動模式進行描述，通過計算轉移概率模型完成輸入交互，在進行輸入交互以后進行交互多模型的輸入，對概率狀態模型進行更新，得到多個模型狀態和對應協方差的狀態估計值并將結果輸出。

假設相應的Markov 模型的轉移概率矩陣T=[πij](i,j=1,2,···,m)和各模型概率矩陣U=1,2,···,m;n=1,2,···,N)，其中，m為模型數，N為粒子數。IMMPF 的具體運算流程[13]如下。

1)隨機抽取粒子。依據室內定位系統中粒子的狀態，設定粒子的狀態值和協方差為

2)輸入交互。對系統中的粒子進行交互輸入。

4)概率模型更新。

5)殘差重抽樣。復制粒子中較大的粒子，以便于減少權值產生新的樣本，進而獲得高效的計算和較低計算協方差。

6)輸出交互。對樣本空間中的粒子輸出交互：

2.3 對IMMPF 進行改進

本文提出改進的IMMPF 算法，在狀態更新中融合了對LOS 和NLOS 信道參數的估計[14]，有效地避免了NLOS 干擾對于無線室內定位的結果擾動。同時，當定位目標非線性增加時，系統中的噪聲會變大，IMMPF 算法無法表示真實的概率密度函數分布。本文通過將改變粒子權重值向似然函數峰值靠近，通過改變粒子的權重占比以及增大粒子數目進一步改變粒子的有效性。改變似然函數的分布與粒子的權重值相對應，相對于IMMPF算法就是權值更新做自適應調整。核心算法結構框圖如圖2 所示。

圖2 改進的IMMPF 算法流程

在進行模式匹配濾波器時，在其中融合了對LOS、NLOS 信道參數估計，同時考慮對于異型空間室內定位出現墻體等干擾造成的NLOS 環境干擾。這樣可以有效避免NLOS 環境中的定位誤差對于定位的干擾，提高異型空間室內定位的精度。主要流程如下。

1)從k時刻初始狀態中采集相應的粒子根據獲得的殘差分別計算相應的NLOS、LOS 情況下的狀態估計及相應的似然函數

2)根據計算出來的數值對于信道概率與信道模型進行融合

3)將結果分別進行濾波以及重采樣，得到相應的目標狀態更新。

根據目標運動模型，可知第j種運動模型的預測狀態為

式中 ωj(k)為系統噪聲輸入。

再根據距離差可以得到觀測噪聲誤差為

由計算測量噪聲分布情況可以得到似然概率為

根據IMM 算法，由似然概率系數可以分別計算LOS 和NLOS 信道概率：

式中

其中，φj,i為信道模型的轉移概率矩陣中的元素，ηj,i,m(k)為信道的概率模型。

將不同信道混合并且結合目標運動狀態測量方程可以得到新的測量殘差及對應的方差：

對粒子進行重采樣，此時可以獲得重要性權重的似然函數[15-16]：

對于多徑的聯合重要性權重：

對于重要性權重進行歸一化處理以及重采樣，可以得到新的狀態估計以及誤差協方差矩陣。

3 實驗與仿真與結果分析

為驗證本文所提算法的定位誤差，對于IMMPF算法、交互式多模型擴展卡爾曼濾波（interactive multiple model extended Kalman filtering，IMMEKF）算法以及改進的IMMPF 算法分別在定位空間內進行仿真實驗。這里的勻速模型為

勻速轉彎模型為

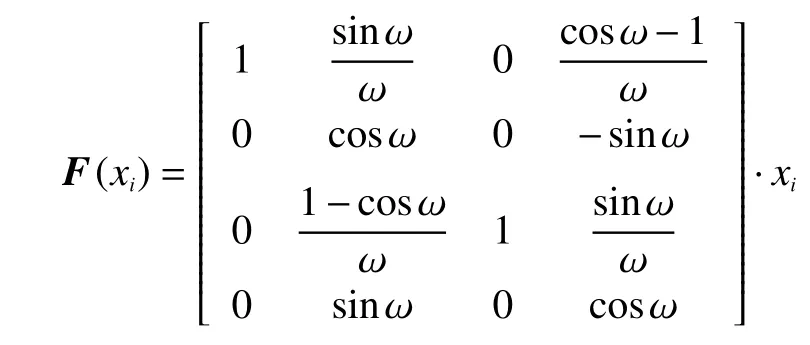
量測模型為

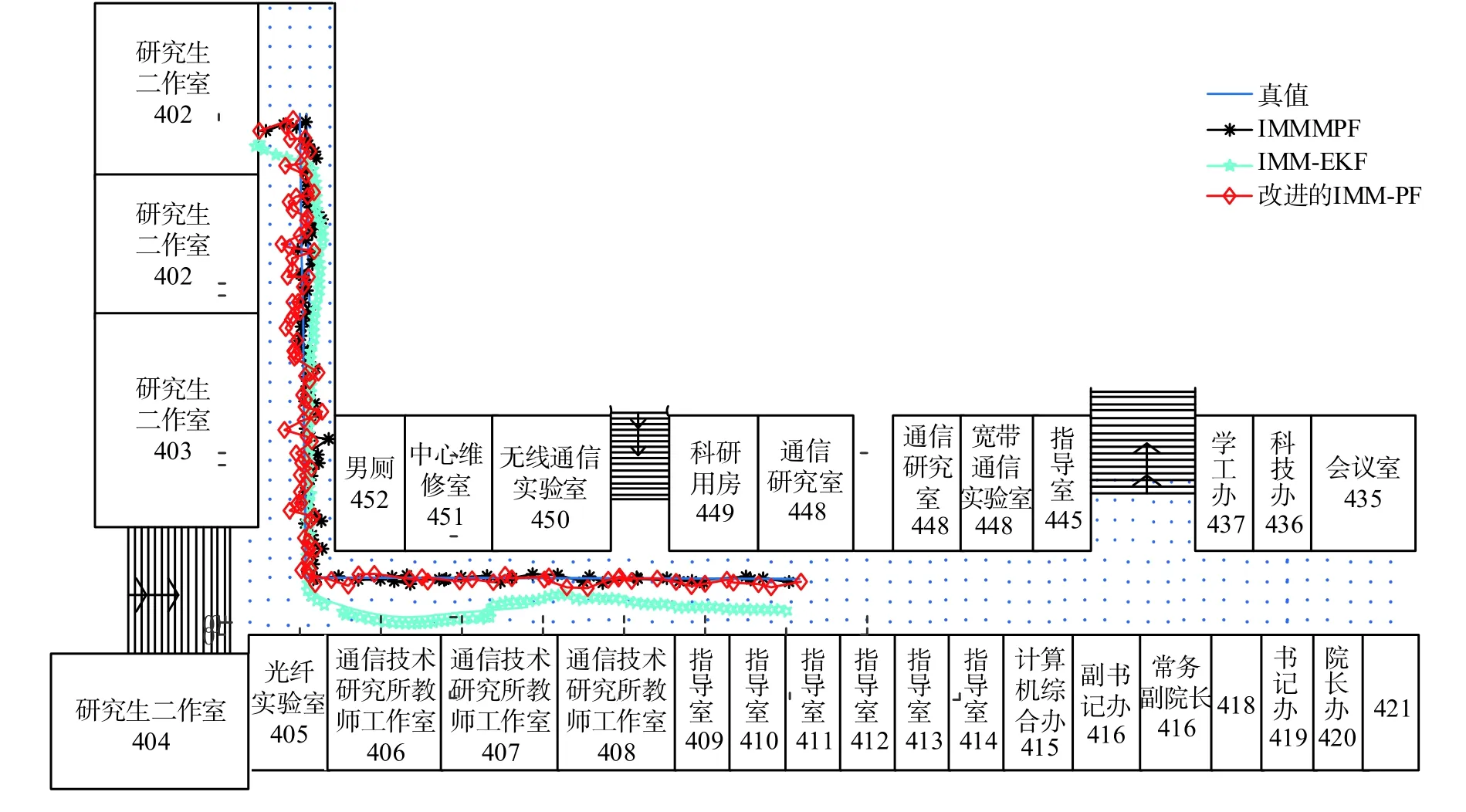
圖3 基于IMM 的3 種算法仿真

由圖3 可以得知，在定位的起始點，其定位的波動性比較大，主要是由于定位初期獲取信息較少，會出現較大的跟蹤誤差。隨著粒子不斷更新，最終誤差穩定在1～2 m。針對IMMFP、IMMEKF和改進的IMMFP 這3 種定位算法，分析每個定位點的位置誤差，如圖4 所示。在各種定位算法中，定位平均誤差數據如表1 所示。

圖4 基于IMM 的3 種算法的定位誤差

從表1 可以看出，在各種定位算法中，平均定位誤差最低的是改進IMMPF 融合定位算法，平均誤差為1.38 m。平均定位誤差的定位精度比傳統的IMMPF 算法提高26.984%，比傳統IMMEKF 算法提高了36%，從而證明了該融合算法的有效性。

表1 不同定位算法平均定位誤差對比

圖5 與圖6 分別為誤差累積圖以及改變粒子數目的定位誤差圖。

圖5 基于IMM 的3 種算法的誤差累積曲線

由圖6 可以看出，當粒子數目適當增大時，可以通過增大粒子濾波算法執行時間提高定位精度。但是粒子數目不是無限增大的，當粒子數目增大一定數目時，會增加預測時間和粒子的更新時間。

圖6 基于IMM 的3 種算法改變粒子數目的誤差曲線

經由上述結果可以得出：對于復雜空間的定位，非視距和多徑效應等干擾，傳統IMMEKF 定位算法不能很好地適用于定位環境中；IMMPF定位算法更適用于多變的環境中，定位精度較高。

為了進一步驗證改進的IMMPF 定位算法效果，改變物體的運動模式進行實驗驗證。保持其他采樣條件不變，改變物體的運動模式，先進行勻加速直線運動，轉彎；然后進行勻速直線運動，得到定位仿真如圖7—圖9 所示。

圖7 IMMPF 與其改進算法定位仿真對比

圖8 IMMPF 與其改進算法定位誤差對比

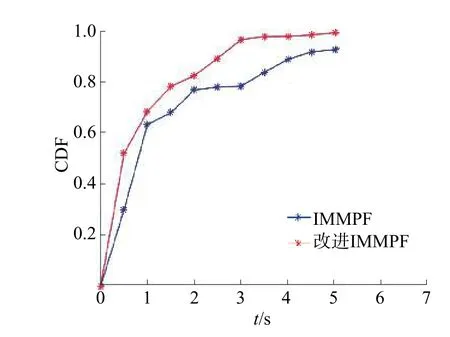
圖9 IMMPF 與其改進算法定位誤差累積曲線對比

4 結論

目前，可以依靠衛星系統等實現室外高精度定位，但由于存在墻體、多徑效應以及NLOS 干擾問題，衛星系統等無法應用于復雜的室內環境，進而無法應用在室內定位技術中。

1)針對NLOS 環境，研究了室內WIFI 信號在室內空間的動態變化。基于傳統的高斯濾波算法改進得到的濾波算法，可以有效地對RSSI 奇異值進行處理，并且可以避免數據丟失對定位的影響，驗證了本文所提定位算法的有效性。

2)考慮到復雜空間內定位目標運動的復雜性，在交互多模型中，利用粒子濾波在定位中的實時性更新中混合信道參數同時對于NLOS 及其LOS 混合信道進行參數估計，同時改變粒子權重值向似然函數靠近，及時通過擴大粒子的權重占比和增大粒子數目，以改變粒子的有效性，這樣提高了改進算法的定位準確性。

通過實際環境對改進的IMMPF 定位算法進行仿真實驗，對于室內目標進行跟蹤定位，充分考慮到室內目標運動具有多種模式、復雜環境的NLOS 干擾以及粒子枯竭問題。在目標環境較為復雜時，改進的交互多模型粒子濾波算法可以對于定位得到達到次優解中的最優結果。通過實驗仿真可以看出，改進的IMMPF 算法能夠很好地在異型復雜環境中實現高精度定位，且該算法可以在復雜環境實現多種模式跟蹤定位，對于無線電監測和管理工作具有重要意義。