TiB纖維分布的均勻性對鈦基復合材料拉伸性能的影響

黃立清,李 超,郭 薇,丁永峰，李 健,3

(1.湖南金天鈦業科技有限公司 湖南省高端裝備特種鈦合金工程技術研究中心，湖南 常德 415001)

(2.龍巖學院, 福建 龍巖 364012)

(3.福建省焊接質量智能評估重點實驗室, 福建 龍巖 364012)

輕質高強的零部件有利于促進機械裝備的減重,從而有效地提高能源利用效率，在汽車、飛機、能源動力等領域具有重要應用。輕質高強零部件的開發主要依賴于高強韌結構材料的應用。在金屬材料領域，復合材料強化法被普遍認為是既能有效提升材料強度、剛度與硬度，又能在一定程度上保持金屬基體固有塑性的辦法[1,2]。連續纖維增強金屬基復合材料具有高的強度和剛度，而非連續纖維/顆粒增強金屬基復合材料具有各向同性的優點。

對于非連續增強鈦基復合材料，由于鈦本身為活潑屬性，可通過原位自生法獲得TiB短纖維、TiC顆粒及Ti5Si3顆粒等增強鈦基復合材料[3, 4]。通常，可通過將硼化物、碳化物及硅化物等粉末與鈦粉或鈦合金粉進行機械合金化，然后對復合粉末進行熱壓、放電等離子燒結或熱擠壓等制備致密的鈦基復合材料[5, 6]。在燒結的過程中，鈦粉與硼化物、碳化物及硅化物等顆粒發生化學反應而快速生成增強相TiB短纖維、TiC顆粒及Ti5Si3顆粒等。然而，由于鈦粉的性質過于活潑，高能的機械合金化過程給鈦粉末或鈦合金粉末帶來較大的污染；因污染而引入的雜質元素(O、N)在鈦基體中具有強的強化與脆化作用，使得機械合金化制備法的過程難以控制且最終產品的塑性差[7]。L J Huang等[8]避開機械合金化，通過將鈦合金粉與硼化物粉末進行簡單的機械混合后進行熱壓，制備了一種具有網狀分布的TiB短纖維增強鈦基復合材料，獲得較高的抗拉強度并保持有鈦基體一定的塑性。L Q Huang等[9, 10]通過將鈦粉或鈦合金粉與納米硼化物粉末進行簡單的機械混合，然后在不同的溫度區間進行放電等離子燒結，獲得了具有網狀編織分布的TiB纖維(長度5～30 μm)增強鈦基復合材料，且其具有高的韌性。這些研究證實了該類制備方法是當前制備非連續增強鈦基復合材料的最佳選擇之一。

受制于加工工藝、增強相的形狀及尺寸、增強相與基體的種類及增強相與基體之間的界面結合情況，增強相的分布對于金屬基復合材料的抗拉伸強度和塑性的影響比較復雜。相比于均勻分布，增強相的非均勻分布形式會提高或降低或基本不影響金屬基復合材料的強度與塑性均可見報道[11-14]。因此，在前期研究工作的基礎上，進一步研究原位自生的TiB短纖維在鈦基體中的分布均勻性對鈦基復合材料拉伸性能的影響，以進一步優化鈦基復合材料的性能。

1 實 驗

實驗原料為2種不同粒徑(分別為0～45 μm和75～106 μm)的球形等離子霧化高純鈦粉，純度均≥99.8%。在2種鈦粉中分別添加體積分數(x)為5%、7.5%和10%的高純納米B粉(純度≥99.6%，尺寸<100 nm)，然后裝入混料器(Turbula mixer)中進行低能機械混合。對混合均勻的粉末進行放電等離子燒結，制備TiB纖維增強鈦基復合材料。下文將采用SmallTi-xTiB與LargeTi-xTiB分別代表采用0～45 μm和75～106 μm鈦粉制備的復合材料。此外，以2種純鈦粉直接進行放電等離子燒結制備的純鈦試樣作為參照。復合材料制備過程中，混料工藝為：氬氣保護，轉速120 r/min, 球料比2∶1，混合時間2 h；燒結工藝為：燒結溫度1200 ℃，壓力30 MPa，保溫時間5 min。

為更好地觀察TiB纖維在鈦基體中的分布，對機械拋光后的復合材料進行深度腐蝕，移除部分鈦基體。腐蝕液的成分為86%純水+10%硝酸+4%氫氟酸，腐蝕時間為5 min。通過金相顯微鏡(Leica DM2700M)觀察復合材料鈦基體的晶粒尺寸；通過掃描電子顯微鏡(JEOL JSM 7001F)觀察復合材料中纖維形貌及分布；通過氧氮氫分析儀(TCH-600 O,N and H analyzer)測試復合材料中O、N含量；通過拉伸試驗機(Instron-5584)測試復合材料的拉伸性能。拉伸試樣的標距為8 mm，拉伸速率為10-3s-1。

基于本實驗中獲得的鈦基復合材料的組織結構及材料性質，構建TiB纖維均勻分布和非均勻分布增強鈦基復合材料的模型，并進行仿真計算。復合材料具有周期性邊界條件的代表性體積單元通過Python程序構建，代表性體積單元被導入Abaqus軟件并進行隱式求解。模型中，鈦基體的彈塑性參數由本研究中的實驗結果所得，泊松比則參考文獻資料為0.34[15]；TiB纖維的楊氏模量為427 GPa[16]，泊松比為0.15[16]。此外，由于Ti/TiB界面具有共格屬性[17]，模型中選用的Ti/TiB界面為緊密結合界面。

2 結 果

2.1 實驗結果

金相觀察下，制備的復合材料均全致密，且Ti基體的晶粒尺寸均約為15 μm。其中，采用細鈦粉制備的SmallTi-xTiB復合材料中氧含量約為0.20%，氮含量<0.01%(質量分數，下同)；而采用粗鈦粉制備的LargeTi-xTiB復合材料中氧含量約為0.16%，氮含量<0.01%。SmallTi-xTiB復合材料的氧含量稍高于LargeTi-xTiB，這主要是由于鈦粉末越細小，比表面積越大，制備過程中更容易被污染。

圖1為SmallTi-7.5TiB和LargeTi-7.5TiB復合材料被深度腐蝕后的顯微形貌。2種復合材料中，TiB短纖維的尺寸基本一致，平均長度約為30 μm，直徑約為2 μm(因TiB纖維的橫截面為六邊形[8, 9]，此處直徑為六邊形的外接圓直徑)。在由粗鈦粉制備的LargeTi-7.5TiB復合材料中(圖1c、1d)，TiB纖維形成了一種中空的網狀分布結構。這種結構是由于TiB在鈦粉原始顆粒邊界形核并向周圍生長而形成的[9]。在由細鈦粉制備的SmallTi-7.5TiB復合材料中(圖1a、1b)，由于原料鈦粉尺寸(0～45 μm)與纖維長度(約30 μm)相近，導致這種網狀結構并不明顯。TiB短纖維可被認為近均勻的分布在鈦基體中。

圖1 腐蝕后SmallTi-7.5TiB和LargeTi-7.5TiB復合材料的顯微形貌

圖2為鈦基復合材料及純鈦的拉伸應力-應變曲線。表1為鈦基復合材料的力學性能測試結果(多個試樣的平均值)。隨著TiB纖維體積分數的增加，復合材料的楊氏模量(E)、屈服強度(Rp0.2)及抗拉強度(Rm)均隨之上升，而伸長率(A)隨之下降。對比近均勻(SmallTi-xTiB)與非均勻(LargeTi-xTiB)鈦基復合材料，在TiB體積分數相同的情況下，前者的屈服強度和抗拉強度稍高于后者，但前者的伸長率明顯高于后者；且隨著TiB體積分數的增加，二者伸長率的差距增大。當TiB纖維體積分數從5%增加到10%時，二者伸長率的差異由0.8%提升到8.6%。

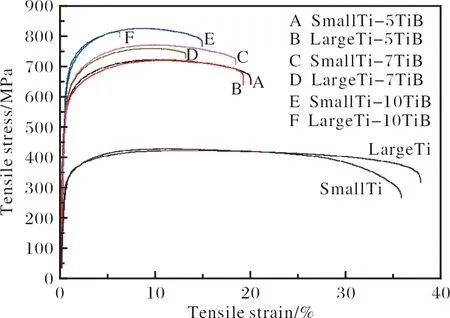
圖2 鈦基復合材料及純鈦的拉伸應力-應變曲線

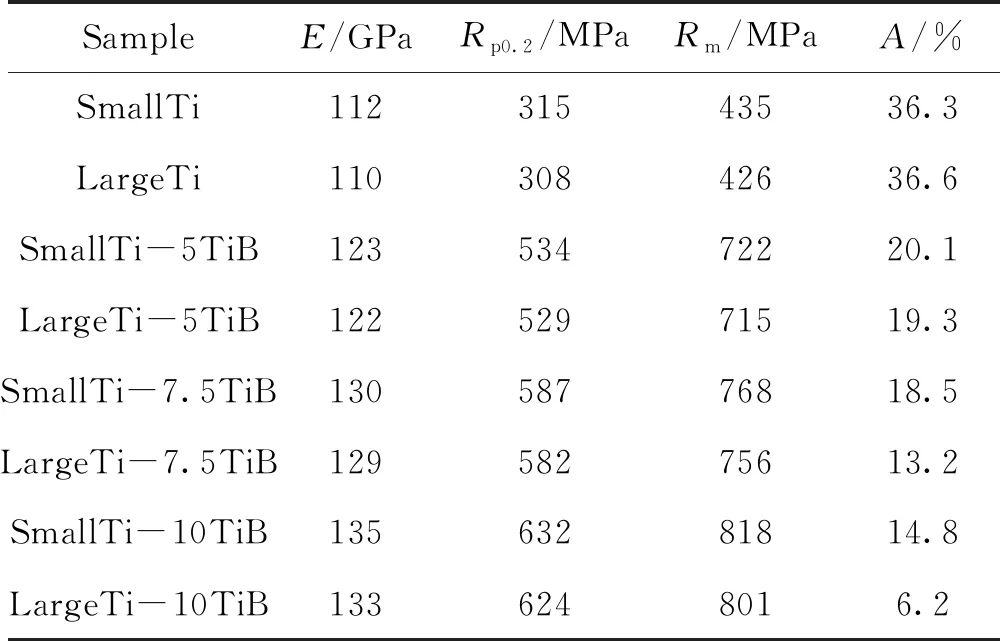
表1 制備的鈦基復合材料及純鈦的力學性能測試結果

2.2 模擬結果

通過有限元模擬進一步研究TiB纖維的分布對鈦基復合材料拉伸性能的影響。基于上述實驗數據構建代表性體積單元，并進行了大量的簡化與假設。模型設置如下：① 代表性體積單元為邊長70 μm的正方體(其體積接近直徑為75～106 μm球形粉末的平均體積)；② TiB纖維在鈦基體中均沿拉伸的軸線方向分布(若纖維取向采用隨機分布，則在纖維數量不多的情況下，纖維在空間上各個方向的整體取向無法均勻一致，使得2個模型的力學性能難以相互比較)；③ TiB纖維外接圓直徑為2 μm(且假定纖維為正六邊形)及長度為15 μm(因纖維取向由實驗中的隨機分布改為模擬中的同向分布，本處參照文獻報道的2種纖維取向的強化效果差異，相應縮短其長度[18])；④ 對于非均勻分布的TiB纖維，其在代表性體積單元內分布在距離單元表面20 μm內的區域，即單元中心50 μm×50 μm×50 μm的區域中僅有鈦基體組織(參考圖1d中TiB在網狀結構中的分布并做近似處理)；⑤ 實驗中SmallTi-xTiB復合材料中TiB纖維為近均勻分布，但在對應模型中對TiB纖維采用均勻分布；⑥ 2個模型中鈦基體的彈塑性參數均采用上述實驗中SmallTi的結果(消除2個模型之間基體差異對模擬結果的影響)；⑦ 任意2根TiB纖維之間最近的距離不小于1 μm(滿足網格劃分與計算要求)；⑧ 復合材料彈塑性行為的求解基于TiB纖維彈性性質和基體彈塑性性質的簡單耦合，僅計算應變為0%～1%的行為(由于模型忽略了塑性變形中纖維/基體界面開裂及纖維斷裂等復雜情形，塑性應變大時計算的失真度大)。TiB纖維均勻分布和非均勻分布的Ti-7.5vol%TiB復合材料的代表性體積單元如圖3所示。代表性體積單元中心區域(50 μm×50 μm×50 μm)全部為基體組織。

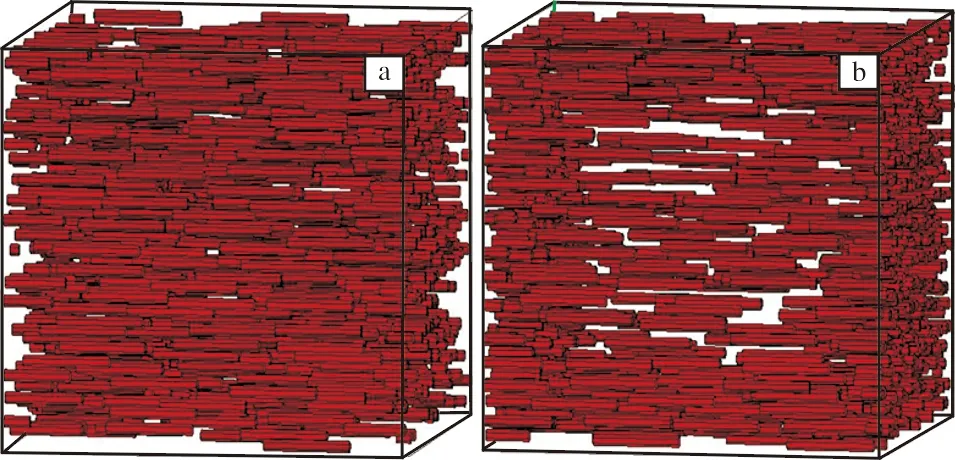
圖3 Ti-7.5vol%TiB的代表性體積單元(70 μm×70 μm×70 μm，顯示纖維和單元輪廓)

圖4為TiB(7.5 vol%)纖維均勻與非均勻分布的鈦基復合材料模型的模擬拉伸應力-應變曲線。在1%的應變內，2種模型的楊氏模量和抗拉強度基本相當，其中抗拉強度的差別在2 MPa以內。2種模型的楊氏模量均約為133 GPa，屈服強度均約為521 MPa。模擬結果與上述實驗結果具有一定的差異，這主要來自于模型的簡化與假設。但是，均勻與非均勻2個模型之間可以進行對比分析。

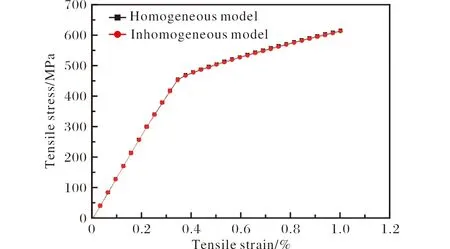
圖4 TiB(7.5 vol%)纖維均勻與非均勻分布的鈦基復合材料模擬拉伸應力-應變曲線

圖5給出了當應變為0.4%時(開始進入塑性變形階段)，2種模型內部的米塞斯應力和最大主應力分布。從圖5a和5b中可以看出，在纖維兩端附近基體中的米塞斯應力較高，而在纖維側面附近基體中的米塞斯應力較低。在纖維均勻分布的模型中，基體中的米塞斯應力在空間整體分布也更均勻；在非均勻模型中，存在著米塞斯應力較高或較低的大塊連續區域。圖5c和5d主要展示了復合材料的最大主應力分布。可以看出，在基體中，最大主應力較大的區域一般在纖維兩端附近，且非均勻模型中基體的最大主應力>400 MPa的區域尺寸多于均勻模型。由于基體的單元格中最大主應力的方向與拉伸軸方向一致，因此這表明在非均勻模型中纖維/基體界面附近區域的法向張應力的聚集程度較均勻模型大。在TiB纖維中，纖維的中部是應力最集中的位置。而且，TiB纖維分布的均勻性影響纖維之間應力的分布。相比于均勻模型，在非均勻模型中不同位置的纖維之間，最大主應力的分布存在著明顯差異。

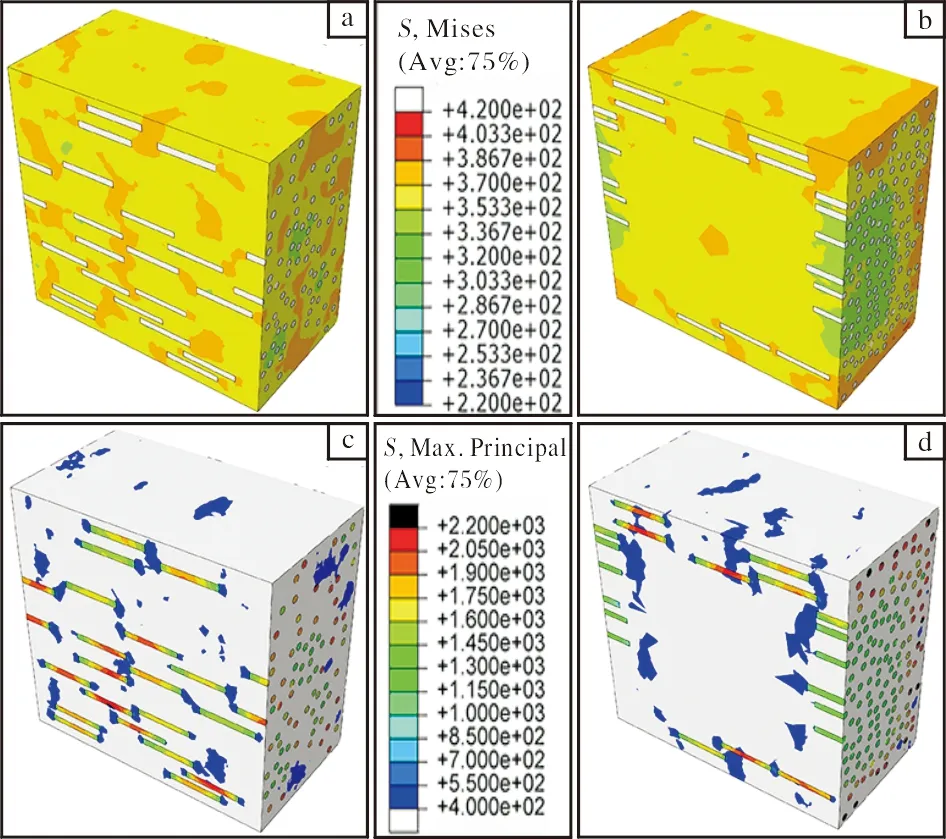
圖5 0.4%應變下均勻模型和非均勻模型中米塞斯應力和最大主應力分布

表2給出了均勻模型和非均勻模型Ti基體的米塞斯應力和TiB纖維的最大主應力的平均值和最大值。從表2中可以看出，2個模型基體的平均米塞斯應力相當，僅在最大米塞斯應力上稍有差異。在均勻模型中，TiB纖維最大主應力的平均值(1751 MPa)稍高于非均勻模型(1740 MPa)，但是前者中TiB纖維最大主應力的峰值(2575 MPa)明顯低于非均勻模型(2878 MPa)。這是由于在非均勻模型中不同位置的TiB纖維受力不均，因而出現一些處于高應力狀態的纖維。以2200 MPa應力為例，在均勻模型中某個單元格的最大主應力高于此值的纖維的數量為78根，而在非均勻模型中纖維數量達到了164根(代表性體積單元中纖維的總數為660根)。

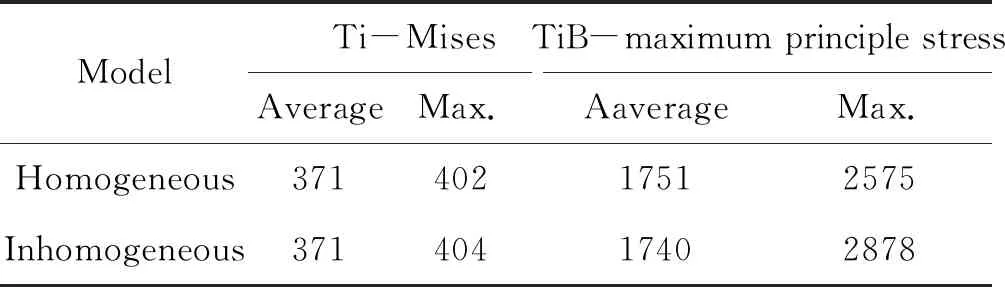
表2 均勻模型和非均勻模型在0.4%應變下的應力統計(MPa)

3 討 論

采用細鈦粉制備的SmallTi-xTiB復合材料的氧含量稍高于采用粗鈦粉制備的LargeTi-xTiB復合材料(氧含量高出約0.04%)。根據理論公式Δσ=0.02Gc1/2(其中G是Ti基體剪切模量，c是氧原子占比)[19]，氧含量差異導致SmallTi-xTiB復合材料的強度比LargeTi-xTiB復合材料高出約7 MPa。拉伸實驗結果表明，在TiB體積分數相同時，纖維近均勻分布的SmallTi-xTiB復合材料的屈服強度和最大強度比纖維非均勻分布的LargeTi-xTiB復合材料稍高(不超過20 MPa)。考慮到2種復合材料其他方面的組織接近，因此可推斷出TiB纖維分布的均勻性對鈦基復合材料強度的影響很小。模擬結果證實了纖維均勻分布與非均勻分布的2類復合材料的楊氏模量和屈服強度基本一致。

實驗表明，纖維非均勻分布的鈦基復合材料的拉伸塑性明顯低于纖維近均勻分布的鈦基復合材料，尤其是纖維體積分數越高這種差異越明顯。當TiB體積分數為10 vol%時，近均勻復合材料的伸長率為14.8%，明顯高于非均勻復合材料的伸長率(6.2%)。復合材料沿纖維軸向受拉時，部分載荷通過剪切機制從基體轉移到纖維上，在纖維長度方向的中間位置出現應力集中，而在纖維兩端的基體處，出現界面法向張應力的集中[20, 21]。本研究中的模擬結果證實了這一受力狀況。由于纖維與基體之間存在上述的作用機理，當纖維的兩端靠近時，可造成基體中應力集中區域的疊加。纖維分布不均時，基體中局部應力集中區域疊加的程度加劇。此外，由于纖維分布不均導致不同區域纖維數量不一致，在纖維少的局部區域，單根纖維承載的載荷增加，纖維內部的應力升高。

基體的米塞斯應力分布不均代表著基體的協調變形能力更差，基體在高應變下更容易發生變形失穩而產生裂紋的形核與擴展。基體中出現最大主應力集中表明局部變形加劇，且由于最大主應力的方向與纖維的軸向一致，使得纖維端面和基體的結合界面在法向張應力導致的張應變下更易被撕裂，形成復合材料內部的裂紋源。此外，單根纖維內部局部的最大主應力(軸向應力)的過高造成纖維本身斷裂的風險加劇[21]。隨著TiB體積分數的增大，局部聚集的TiB纖維更多，相當于纖維分布的不均勻性加劇。這些因素解釋了實驗中纖維不均勻分布的LargeTi-xTiB復合材料的拉伸塑性比纖維近均勻分布的SmallTi-xTiB復合材料更低，而且隨著TiB纖維體積分數的增加，二者塑性的差距加大。當TiB纖維體積分數從5%增加到10%時，二者伸長率的差異由0.8%提升到8.6%。由此可以推斷，當TiB纖維體積分數在10%以上時，二者塑性的差別可能更大；而TiB纖維體積分數在5%以下時，二者塑性的差別較小。

以上初步研究了TiB纖維分布的均勻性對純鈦基復合材料拉伸性能的影響。由于TiB纖維非均勻分布帶來的上述3個影響要素(基體中米塞斯應力分布均勻性降低，纖維/基體界面附近的法向張應力增加，以及TiB纖維上的最大主應力的峰值升高)對復合材料的塑性均不利，因此可以推斷TiB纖維的非均勻分布對鈦基復合材料的塑性均不利。當然，由于本實驗未深入研究3個影響要素之間的主導關系，且當基體類型發生變化時材料的力學行為會發生改變，因此TiB纖維的非均勻分布對其他鈦基復合材料拉伸塑性的影響程度可能發生變化。可通過實驗進一步研究TiB纖維增強鈦基復合材料中復合材料拉伸斷裂失效的主導機理，以更好地指導非連續纖維增強鈦基復合材料的設計。

4 結 論

(1) TiB纖維分布的均勻性對鈦基復合材料的抗拉伸強度和楊氏模量影響均很小。

(2) TiB纖維非均勻分布鈦基復合材料的拉伸塑性低于近均勻鈦基復合材料；且隨著纖維體積分數增加，二者塑性的差距增大。

(3) 相比TiB纖維均勻分布的鈦基復合材料，非均勻鈦基復合材料基體中的米塞斯應力分布更不均，纖維/基體界面附近的法向張應力加劇，TiB纖維上的最大主應力的峰值更高，鈦基復合材料中裂紋形成的風險更高。