纏繞彎曲多次循環下連續油管疲勞壽命仿真分析*

呼煥苗，曹銀萍※，韋 亮，牛占山，潘 瑩，竇益華，鄭 杰

（1.西安石油大學機械工程學院，西安 710065；2.中國石油西部鉆探試油公司，新疆克拉瑪依 834000）

0 引言

連續油管（Coiled－Tubing，CT）是相對于用螺紋連接下井的常規油管而言的，是卷繞在滾筒上拉直后直接下井的長油管[1]。由于連續油管能夠大幅度節省作業時間和作業成本，目前廣泛用于油田鉆井、完井、壓裂、酸化、排液、試油、采油采氣、修井等領域[2]。連續油管作業時，在井中起下一回都要經歷6次拉直—彎曲塑性變形，極易發生疲勞失效[3－4]。近年來，隨著對一些高溫高壓高深井的勘探，連續油管的應用越來越廣泛。因此，研究不同內壓下連續油管纏繞/彎曲作用發生塑性變形進而會發生低周疲勞具有重大的實際意義。

目前，連續油管疲勞壽命通常都是采用疲勞壽命理論模型、室內疲勞實驗以及現場試驗等方法。2001年，王優強等[5－6]建立了半經驗公式的連續油管壽命預測模型。2004年，朱小平[7]以塑性力學理論為基礎，進行了連續油管在循環彎曲作用下疲勞壽命的研究。2006年，Tipton等[8]根據Miner理論建立了連續油管疲勞壽命預測模型。2008年，王海濤[9]首次結合連續油管的應力狀態，將三參數冪函數能量法用于疲勞壽命預測。2012年，李子豐等[10]通過對預彎曲連續油管的受力分析和強度校核，建立了預彎曲連續油管疲勞壽命預測模型。2017年，賀海軍[11]等用ANSYS Workbench有限元分析軟件建立了滾筒處的連續油管三維有限元力學分析模型。2017年，竇益華[12]等通過分別考察不同松弛角度和鋼級的連續油管彈塑性極限彎矩以及彈性極限彎曲半徑等力學性能，得出當松弛角度在45°～50°時，連續油管會獲得較好的力學性能。2018年，于桂杰[13]等利用人工神經網絡對有表面缺陷的連續油管進行疲勞壽命預測。Tian等[14]提出一種改進的擴展有限元（IXFEM）方法，從根本上克服了標準XFEM和修正XFEM的線性依賴和病態問題。上述文獻雖然對連續油管疲勞壽命預測模型進行了修正，但是沒有涉及到不同工況，因而有必要研究連續油管在內壓作用下的疲勞壽命。

在實際應用中，連續油管帶內壓工作時的失效故障時常發生，尤其是壓裂工況。本文基于ABAQUS/FE－SAFE軟件，對不同內壓下纏繞/彎曲連續油管進行了疲勞壽命分析。

1 纏繞/彎曲連續油管有限元模型的建立

考慮到多次纏繞/彎曲過程中施加內壓的情況下，連續油管的疲勞壽命會受到影響，所以進行了纏繞/彎曲過程中的仿真分析。以QT－900作為研究對象，基于美國Stewart&Stevenson公司的連續油管疲勞試驗機工作原理進行仿真分析[15]。連續油管纏繞/彎曲有限元模型如圖1所示。圖1（a）為連續油管纏繞在滾筒上的尺寸以及連續油管、滾筒、校直模的位置，其中連續油管長度為800 mm，滾筒的半徑為1 375 mm，矯直模的長度為550 mm。根據上述尺寸創建三維有限元模型，其中，有連續油管、滾筒、滾輪和擋板，為了簡化模型，將滾筒用彎曲板代替，矯直模用擋板代替，彎曲拉直用滾輪驅動來實現，具體的有限元模型如圖1（b）所示。

圖1 連續油管纏繞/彎曲有限元模型Fig.1 Finite element model of coiled tubing winding/bending

2 纏繞/彎曲連續油管有限元分析

2.1 材料屬性設置

使用ABAQUS對連續油管的彎曲—拉直力學行為進行有限元模擬分析，以QT－900連續油管進行疲勞壽命分析，其材料屬性如表1所示。

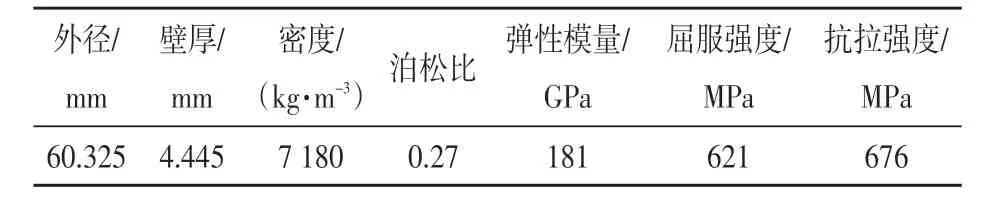
表1 QT－900連續油管材料參數Tab.1 QT－900 coiled tubing material parameters

2.2 網格劃分

為了簡化模型，將滾筒和矯直模使用殼單元進行創建并設置為剛體。給連續油管的有限元體單元模型進行材料屬性的設置。采用三維八節點減縮積分單元即C3D8R單元進行網格劃分，單元選擇實體單元；減縮積分單元在彎曲載荷下也不易發生單元過于剛硬的問題，還能顯著提高計算效率。同時為了提高計算的精度，對連續油管的厚度方向設置兩層六面體網格，其他部件均設置為剛體，網格類型為4結點的三維雙線性剛體四邊形即R3D4。

2.3 施加邊界條件和計算

采用靜態通用算法進行有限元計算，設置兩個分析步，一是彎曲分析步，二是矯直分析步，設置的時間均為0.1 s。模型中的接觸通過相互接觸的面之間定義接觸對來實現，設置連續油管與滾筒面—面接觸對，連續油管與矯直模面—面接觸對以及連續油管與滾輪之間面—面接觸對，設置滾筒、矯直模和滾輪為主面，連續油管為從面。接觸屬性設置法向和切向行為，法向設置“硬”接觸，這樣可以防止連續油管穿過剛體模具；切向設置摩擦因數，模擬設置因數為0.1。這里對連續油管未設置載荷而是設置邊界條件。圖2所示為邊界條件的設定，將連續油管的一端、滾筒和矯直模固定，給滾輪設置位移，彎曲分析的時候給上滾輪設置向下的位移，矯直分析的時候給下邊的滾輪設置向上的位移，將兩個滾輪分別耦合到自己的參考點上。另外，給滾輪設置了轉動慣量，一個剛體，如果在所有自由度上有一個任意自由度方向沒有被約束住的話，那么在受到載荷時，在這個自由度上必然出現無窮大的位移。即使受到一個很小的力，也會在這個自由度上產生無窮大的加速度，即產生無窮大的位移，所以對剛體通過設置轉動慣量來設置質量。

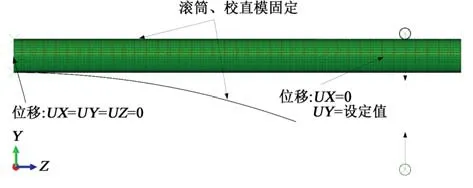
圖2 邊界條件設置Fig.2 Boundary condition setting

2.4 不同內壓下連續油管仿真計算結果分析

為了考察不同內壓下連續油管的疲勞壽命情況，對連續油管的管內設置不同的壓力進行三維有限元建模與計算，在前述力學模型計算得到連續油管彎曲和矯直的基礎上設置位移值，設置向上和向下的位移均為159 mm。在同樣的工況下，分別設置0～80 MPa的內壓，分別計算得到不同內壓作用下連續油管的彎曲—矯直應力應變結果的ODB文件，圖3所示為內壓為20 MPa時的彎曲—矯直云圖。

圖3 內壓20 MPa連續油管有限元計算結果Fig.3 Finite element calculation results of coiled tubing with internal pressure of 20 MPa

通過仿真計算結果分析可知，連續油管在滾筒上纏繞/彎曲是一個復雜的塑形變形過程。連續油管完全纏繞/彎曲狀態下，除彎曲中性層附近的部分，大部分截面已經產生了塑性變形。因此，矯直狀態下會有明顯的殘余應力，殘余應力較彎曲狀態減小。

3 連續油管低周疲勞壽命預測

3.1 Fe－safe疲勞壽命計算

在有限元分析結果的基礎上，利用Fe－safe軟件進行連續油管的疲勞壽命分析。將有限元計算的ODB結果導入Fe－safe，選取兩個分析步當中最后一幀進行計算，計算過程中單位設置一致，材料參數設置和前述有限元模擬當中設置也一致，然后選取有限元模型中連續油管集合進行分析計算。設置表面粗糙度為0.6＜Ra＜1.6，最后選取粗糙度算法，選取默認的Normal Strain：－Morrow算法進行計算。

3.2 連續油管疲勞壽命預測分析

為了考慮壓裂工況下的連續油管疲勞壽命，將不同內壓下的有限元計算結果按照上述計算過程進行疲勞壽命的計算，得到0～80 MPa壓力下的疲勞壽命結果，圖4所示分別為20 MPa和70 MPa內壓下的計算結果云圖。

圖4 20 MPa和70 MPa內壓下連續油管疲勞壽命云圖Fig.4 Fatigue life cloud of coiled tubing at 20 MPa and 70 MPa internal pressure

為了直觀地得到連續油管疲勞壽命隨內壓變化的趨勢，依據仿真結果繪制了不同內壓下連續油管疲勞壽命曲線圖形，如圖5所示。可以直觀地看到，隨著內壓的不斷增大，連續油管循環次數呈現非線性下降的趨勢，沒有內壓的時候約1 000次，當內壓增加到60 MPa時，循環次數約為96次，而當內壓為80 MPa時，循環次數為50次左右。

圖5 不同內壓下連續油管疲勞壽命曲線Fig.5 Fatigue life curves of coiled tubing under different internal pressures

4 結束語

考慮到連續油管彎折作用下會有殘余應力，在壓裂過程中多次彎折作用下會造成塑性變形，進而影響其疲勞壽命。所以采用有限元方法進行了壓裂工況下連續油管纏繞/彎曲低周疲勞壽命分析，得到如下結論。

（1）通過對不同內壓下連續油管纏繞/彎曲有限元仿真分析表明，完全纏繞在滾筒上的連續油管截面大部分進入了塑性區，只有中性軸附近的部分還處于彈性階段。

（2）當內壓增大到10 MPa，循環次數降到855次；當內壓增大到80 MPa，循環次數降到50次，與現有的實驗結果吻合較好，所以有限元仿真方法提供了一種便捷的疲勞壽命分析的思路。

（3）在壓裂工況下，隨著內壓的增大，連續油管的疲勞壽命是呈現非線性下降的趨勢，為了保證壓裂安全，應該合理控制壓裂內壓。為連續油管的現場操作提供安全保障，具有重要實際意義。