靶板強度對射孔彈穿深影響的有限元仿真

徐 浩，李明飛，竇益華

（西安石油大學機械工程學院，西安 710065）

0 引言

隨著完鉆井深的不斷增加，儲層巖石壓實度、強度和地層壓力也不斷增大，普通射孔彈無法達到射孔穿深要求，因此需采用超強射孔彈射穿污染帶。另外，現有方法通常對低強度混凝土靶進行模擬，深井下儲層巖石強度常超過70 MPa，因此需開展射孔彈侵徹高強靶有限元分析。

現有文獻針對射孔彈侵徹高強靶數值分析較少。文獻[1]研究了不同裝藥結構對混凝土穿深的影響，包括藥型罩錐角、藥型罩材料、藥型罩壁厚、藥型罩的曲率半徑、聚能裝藥外殼以及炸高；文獻[2]應用LS－DYNA軟件對某型石油射孔彈裝藥結構下聚能射流形成、侵徹鋼靶過程進行了數值模擬及分析，并與實驗數據作了對比；文獻[3]研究了射孔彈侵徹砂巖靶實驗，分析了藥型罩材料、壁厚、開口角度等因素對穿深的影響。文獻[1－3]為射孔彈侵徹試驗研究。分析可得，實驗成本較高，模擬井下實際工況，建立射孔彈—射孔槍—射孔液—套管—超強砂巖靶模型試驗幾乎沒有。文獻[4]結合室內材料試驗及有限元分析法，分析了不同深度的直井和水平井中套管承受非均勻載荷的力學性能；文獻[5]應用ANSYS/Workbench模塊，建立射孔段管柱三維有限元模型，在井下實測沖擊載荷作用下，分析了管柱的動力響應規律；文獻[6]應用ANSYS/Workbench建立了某規格射孔彈侵徹圓柱體應力砂巖的有限元模型，分析了側向與軸向應力值分別為0、50 MPa時射孔彈侵徹砂巖的深度。文獻[4－6]均為通過力學模型對射孔過程進行分析，但理論分析假設過多，沒有考慮槍、套管、射孔液的影響，結果難免存在偏差。文獻[7]采用LS－DYNA軟件，模擬了矩形射孔彈射流的形成過程及其鋼靶侵徹過程；文獻[8]采用LS－DYNA軟件，模擬了射流成型及其對混凝土靶板的侵徹過程，研究了不同錐角對聚能射流成型和侵徹的影響；文獻[9－11]用LS－DYNA軟件，模擬了射流侵徹過程；文獻[12]用AUTODYN軟件，仿真分析了聚能射流形成、侵徹鋼板過程；文獻[13]應用LS－DYNA軟件對聚能裝藥在不同起爆方式下的射流形成過程進行了三維數值模擬；文獻[14]用AUTODYN對油田使用的射孔彈的爆轟壓垮藥型罩過程和射流侵徹套管過程進行了模擬計算。文獻[7－14]為射孔侵徹的數值仿真研究。分析可得，數值模擬大多只是對射流成型過程進行模擬，并未涉及射流侵徹過程，并未建立完整射孔彈—射孔槍—射孔液—套管—超強靶模型模擬出實際穿深。文獻[15－17]主要研究了ALE算法在相關領域的應用，給出了相關的研究方法和技巧，為本文的研究提供借鑒和參考。

綜上所述，射孔侵徹往往針對普通射孔彈侵徹低強度靶板進行仿真分析，且考慮計算機時問題并未計算至射流終止。本文應用LS－DYNA軟件，結合ALE算法，以某油田深井下射孔為例，建立HS35－5型射孔彈侵徹不同強度混凝土靶三維模型。通過建立非反射邊界條件，消除爆轟波對射流成型和效果的干擾；通過調整關鍵部位網格密度、優化不同接觸面間的網格協調，減少數值畸變，提高分析精度，降低機時。本文研究可為實際井下射孔彈侵徹高強靶的仿真分析提供方法參考。

1 有限元模型建立

1.1 幾何模型

為了研究不同強度混凝土靶HS35－5射孔彈射流射流速度變化及穿深，建立1/4射孔彈—射孔槍—射孔液—套管—混凝土靶模型。模型參數：井深5 500 m、射孔段深度5 000 m，地層壓力梯度1.0，射孔處地層圍壓50 MPa。HS35－5射孔彈參數為：彈高54 mm，射孔彈直徑46 mm，炸藥類型為RDX，裝藥質量35 g，藥型罩高度40 mm，藥型罩外徑36 mm，壓入深度2 mm，罩重100 g；炸高15 mm；套管外徑178 mm，壁厚12 mm；射孔槍外徑102 mm，壁厚6 mm；混凝土靶厚度設置1 200 mm。單枚1/4射孔彈—射孔槍—射孔液—套管—混凝土靶幾何模型如圖1所示。

圖1 1/4 HS35－5射孔彈侵徹混凝土靶三維模型

1.2 三維有限元模型建立及網格劃分

射孔彈—射孔槍—射孔液—套管—混凝土靶模型選擇3D164單元；圖2所示為整個模型有限元網格劃分示意圖，其中射孔彈頭部包括炸藥、藥型罩網格加密；射孔槍、套管、混凝土靶板采用漸變式網格劃分方法，即與射流接觸侵徹部分加密其網格數量，其余部位減少網格數量。其中空氣單元數為65 630、殼體4 500、炸藥3 500、藥型罩2 352、槍管1 000、套管1 080、射孔液800、混凝土靶24 000。

圖2 1/4HS46射孔彈侵徹混凝土靶三維模型網格

1.3 材料模型選擇

1.3.1 炸藥材料

HS35－5射孔彈采用RDX裝藥，選用的材料模型是HIGH＿EXPLOSIVE＿BURN材料模型，炸藥爆炸產生的沖擊波壓力采用JWL方程，其表達式為：

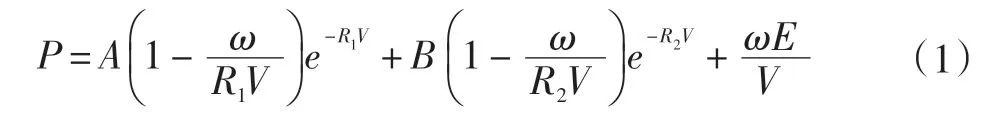
式中：P為等熵壓力；V＝ρ0/ρ＝v/v0為相對比容；A、B、R1、R2、ω為待定常數；E為單位體積的內能。

炸藥密度為1.8 g/cm3，分析參數如表1所示。表中，MID為材料編號：RO為密度；D為爆速；PCJ為Chapman－Jouget壓力；BETA為燃燒標志；K為體積模量；G為剪切模量；SIGY為屈服應力；EOSID為狀態方程ID；A、B、R1、R2、O MEG、E0為炸藥狀態方程參數，這里為定值；V0為初始相對體積。

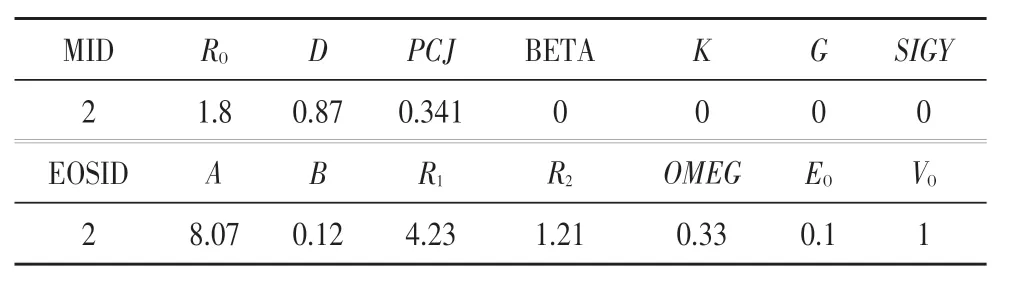
表1 炸藥分析參數（HIGH＿EXPLOSIVE＿BURN）

1.3.2 藥型罩材料

藥型罩的材料為紫銅，固態金屬藥型罩轉化成液態高速金屬流體過程中涉及大范圍固液轉化，選用MAT＿STEEINBERG材料模型。該材料模型在模擬材料變形、狀態轉化等方面較為準確。該模型的特性為屈服強度隨溫度和壓強的變化而變化，在該模型中，剪切模量G和屈服強度σs均隨壓力增大而增大，但隨溫度升高而降低。當材料達到自身熔點時，G和σs都接近0。

材料熔化前的剪切模量G為：

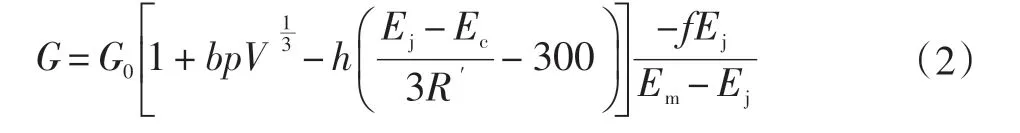
屈服強度σs為：

式中：p為壓力；V為相對體積；Ec為冷壓縮能；Em為融化能；R′＝Rρ/A，R為氣體常數，A為原子量。若Em＞Ej，則有rj為初始塑性應變，當時，令。當材料融化后，σs和G設置為初始值的一半。

藥形罩本構方程采用EOS＿GRUNEISEN，藥型罩材料具體分析參數如表2所示，狀態方程分析參數如表3所示。

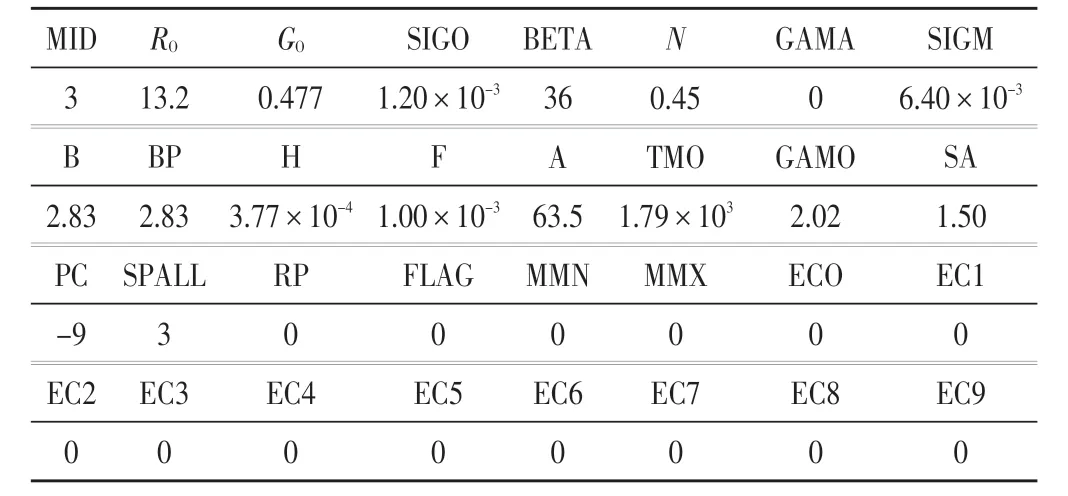
表2 藥型罩材料模型分析參數（MAT＿STEEINBERG）

1.3.3 混凝土材料

混凝土強度為80 MPa，用于模擬深井下巖石儲層，采用JOHNSON＿HOLMQUIST＿CONCRETE模型，分析參數如表3所示。表中，MID為材料編號；RO為密度；G為剪切模量；A為規范內聚強度；B為歸一化壓力；C為應變速率系數；N為壓力硬化指數；FC為準靜態單軸抗壓強度；T為最大拉伸靜水壓力；EPSO為參考應變率；EFmin為斷裂前塑性應變；SFMAX為標準化的最大力量；PC為沉重壓力；UC為破碎體積應變；PL為鎖定應力；UL為鎖定體積應變；D1、D2為損害常數；K1、K2、K3為壓力常數；FS為故障類型。

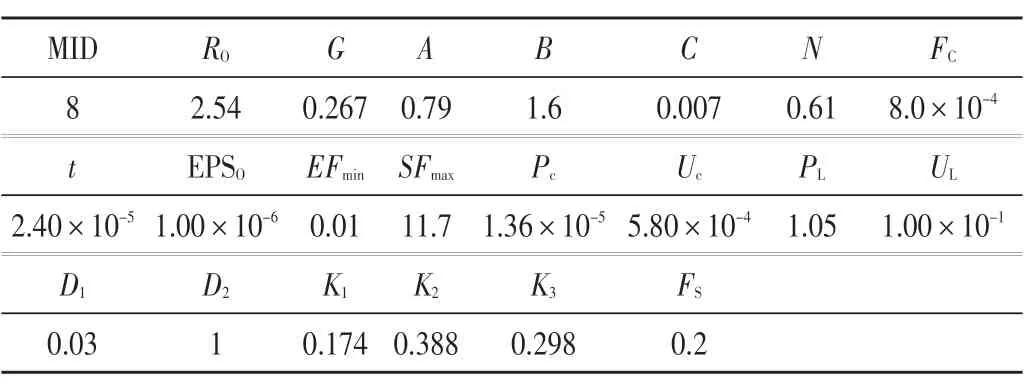
表3 混凝土材料模型分析參數（JOHNSON＿HOLMQUIST＿CONCRETE）

1.3.4 有限元算法設置

有限元模型中，空氣、炸藥、藥型罩、射孔液等在形成超高速金屬射流和射流侵徹射孔槍、射孔液、套管及混凝土靶的過程中，具有大變形和高速流動的特點，運用歐拉算法進行沖擊動力學仿真，對模型的網格精度要求較高，導致計算機時較長，數值分析成本較高；拉格朗日算法雖然對模型網格要求不高，但模擬固液轉化過程質量不高；ALE算法也叫任意歐拉拉格朗日法，其中包含歐拉算法以及拉格朗日算法，對有限元模型中的空氣、炸藥、藥型罩、射孔液采用歐拉算法，細化網格；射孔槍、套管、彈殼、混凝土靶有限元模型采用La?grange算法，相比于歐拉算法，可以減小網格數量，降低機時。實際射孔中，射孔槍與套管、混凝土靶互相之間并不會有所接觸，但在LS－DYNA中，在金屬射流侵徹的過程中，射孔槍與套管、混凝土靶之間通過射流頭部會有接觸的可能，若不設置接觸類型，易導致計算出錯。因此拉格朗日算法單元射孔槍與套管、射孔槍與混凝土、套管與混凝土靶之間均需要設置接觸類型，接觸類型采用ESTS侵蝕接觸。

2 有限元動態仿真過程

圖3給出了金屬射流形成及侵徹過程，炸藥產生的巨大沖擊波在軸線方向疊加給金屬藥型罩施加高溫高壓，藥型罩微元從軸向頂點到側向底邊依次發生變形，在軸線方向上發生激烈碰撞，在尾端形成直徑較大的杵體、前端形成細束金屬射流，射流依次穿過射孔槍，侵徹套管、射孔液、混凝土靶板。圖3（a）所示為藥型罩發生變形形成射流的過程，此時射流沿軸向方向被壓垮，開始形成射流；圖3（b）～（d）分別為金屬射流侵徹槍管、射孔液、套管及混凝土靶狀態。

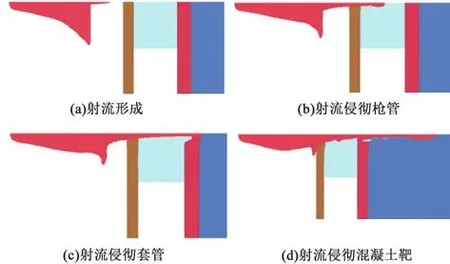
圖3 射孔彈侵徹動態過程

3 不同強度靶板射孔彈侵徹速度分析

3.1 軸向速度

圖4所示為不同靶板強度射流侵徹混凝土靶軸向速度曲線。射流侵徹70 MPa、90 MPa及110 MPa混凝土靶軸向速度曲線趨勢大致相同，27μs時，射流穿過套管開始侵徹混凝土靶，此時射流頭部軸向速度為5 027 m/s，射流在250μs之前速度下降較快，250μs之后速度下降較緩。射流侵徹70 MPa混凝土靶軸向截止速度為600 m/s；射流侵徹90 MPa混凝土靶軸向截止速度為700 m/s；射流侵徹110 MPa混凝土靶軸向截止速度為802 m/s。射流侵徹90 MPa混凝土靶軸向截止速度較70 MPa混凝土靶提高14.3%；射流侵徹110 MPa混凝土靶軸向截止速度較70 MPa混凝土提高33.7%。結果表明，由于靶板強度的提高，相同射流截止軸向速度提高，從而導致射流侵徹能力降低。

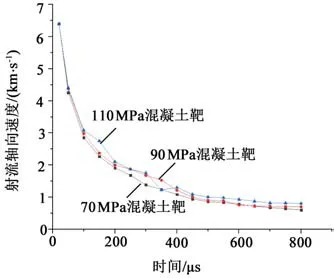
圖4 不同強度混凝土靶射流軸向速度變化曲線

3.2 徑向速度

圖5 所示為射流侵徹不同強度混凝土靶徑向速度曲線。由圖可知，射流侵徹70 MPa、90 MPa及110 MPa混凝土靶軸向速度曲線趨勢大致相同，在侵徹靶板之前，射流徑向速度均為704 m/s，射流徑向速度在250μs之前下降較快，250μs之后下降較緩。與軸向速度不同，射流徑向速度并不是一味下降，而是會出現波動，初步分析為射流在侵徹過程中出現多次斷裂，射流會斷裂成好幾段碎片，只剩頭部繼續侵徹，當射流中部斷裂時，射流碎片將不會繼續向前侵徹，射流碎片所攜帶能量會使射流持續擴孔，從而導致射流徑向速度波動。從3種工況下分析射流徑向速度可以發現，射流侵徹110 MPa混凝土靶徑向截止速度最大，其次為90 MPa混凝土靶，最后為70 MPa混凝土靶。由此可知，靶板強度的增大將會提高射流徑向截止速度，這與射流軸向截止速度分析大致相同。

圖5 不同強度混凝土靶射流徑向速度變化曲線

4 不同強度靶板射孔彈侵徹深度分析

圖6所示為3種工況下選取不同時間點位移，利用Origin軟件所繪制的位移時間曲線。從圖中可以看出，3種工況下射流穿深曲線趨勢大致相同，射流侵徹70 MPa混凝土靶穿深約為670 mm；射流侵徹90 MPa混凝土靶穿深約為640 mm，對比70 MPa混凝土靶穿深下降4.5%；射流侵徹110 MPa混凝土靶穿深約為603 mm，對比70 MPa混凝土靶穿深下降10%。在750μs后，3種工況下射流穿深曲線逐漸平緩，無明顯變化。在開始階段，侵徹速度較快，尤其是在500μs之前，而在600μs后，射流侵徹速度明顯減慢。隨著靶板強度的增加，射孔彈侵徹深度逐漸降低。

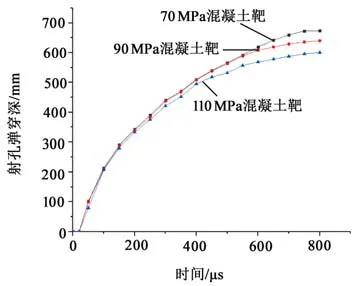
圖6 不同強度混凝土靶射孔彈穿深變化曲線

5 結束語

本文應用LS－DYNA軟件，模擬超深井下工況，建立1/4完整射孔侵徹的三維有限元模型，并在砂巖外圍施加50 MPa圍壓，應用ALE算法，給定炸藥參數，模擬爆轟過程，真正實現了爆轟過程、藥型罩固流轉化、射流高速侵徹套管的大變形和流固耦合仿真，無圍壓下射流穿深與試驗穿深誤差為1.5%，得到如下結論。

（1）通過優化不同接觸面間的網格協調，減少數值畸變，提高分析精度；通過建立1/4射孔彈模型、調整關鍵部位網格密度，減少網格數量，降低機時。

（2）70 MPa混凝土靶射流軸向臨界速度為600 m/s，徑向臨界速度為44.2 m/s；90 MPa混凝土靶射流軸向臨界速度為700 m/s，徑向臨界速度為58.8 m/s；110 MPa混凝土靶射流軸向臨界速度為802 m/s，徑向臨界速度為67.2 m/s。隨著靶板強度的增加，射孔臨界速度提高。

（3）70 MPa混凝土靶射孔彈侵徹深度為670 mm；90 MPa混凝土靶射孔彈侵徹深度為640 mm；110 MPa混凝土靶射孔彈侵徹深度為603 mm。隨著靶板強度的增加，射孔彈侵徹深度逐漸降低。