特種汽車輪邊減速系統齒輪傳動力學特性分析

李 陽，武之劍，朱學斌，李浩鵬

（泰安航天特種車有限公司，山東泰安 271000）

0 引言

特種汽車一般采用主減速器和輪邊減速系統兩級減速來適應低速、高扭等復雜工作環境下的使用要求。輪邊減速系統作為簧下組件，其受力環境更為復雜。

齒輪系統的模型根據研究內容不同有多種分類，如動載系數模型、齒輪副扭轉振動模型、傳動系統模型和完整齒輪系統模型[1－4]。扭轉振動模型因其更簡易的計算方法，常被用于齒輪的傳動軸較大和軸承對齒輪支撐較大的齒輪進行建模。本文以汽車輪邊減速系統齒輪為研究對象，建立單級齒輪動力學模型，基于Runge－Kutta法編程求解，分析單級齒輪的傳動力學特性，為復雜環境下特種汽車輪邊減速系統性能設計提供理論基礎。

1 建立動力學模型

將圖1所示的輪邊減速系統齒輪副簡化為圖2所示的受力簡圖。其中r1、r2分別為主、從齒輪的基圓半徑；I1、I2分別為主、從動齒輪的轉動慣量；θ1、θ2分別為主、從動齒輪的扭轉角位移；T1、T2分別為作用在主、從動齒輪上的扭矩；k(τ)為時變嚙合剛度；Cg為齒輪副的嚙合阻尼；e(τ)為輪齒副的嚙合綜合誤差。

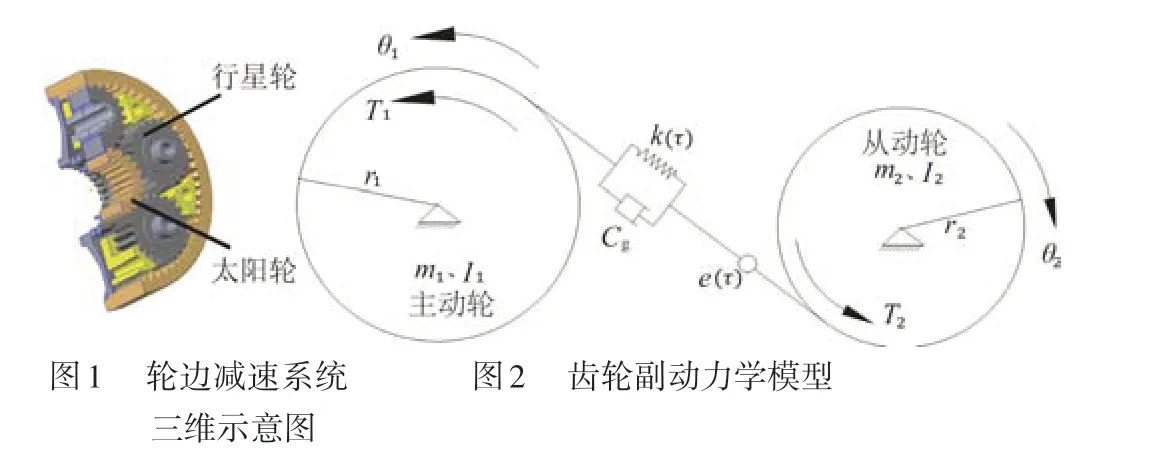
根據牛頓第二定律可以得到系統的運動微分方程組：

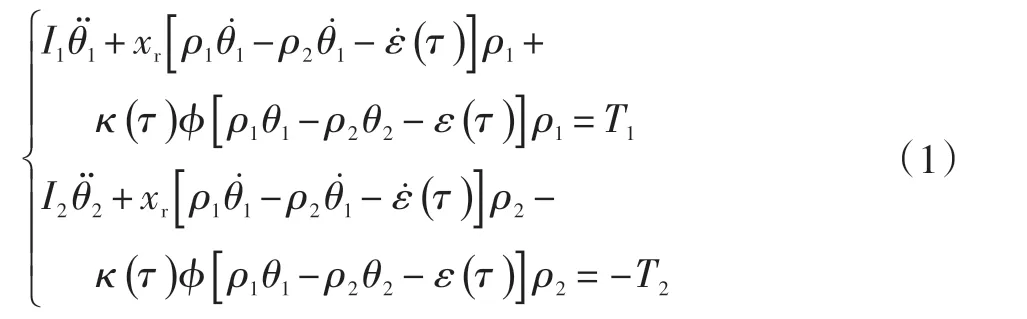
定義主、從動齒輪沿著嚙合線上位移的分別為x1、x2，則：

兩個嚙合齒輪的等效質量表示成mi＝Ii/ri2。聯合式（1）、（2），進一步簡化可得：

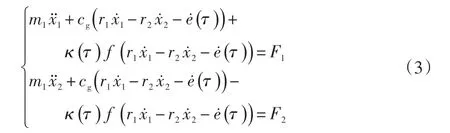
式中：mi為齒輪的當量質量，i＝1為主動齒輪，i＝2為從動齒輪；Fi＝Ti/ri為齒輪i上作用的嚙合力；κ(τ)為齒輪嚙合過程中的時變嚙合剛度；f(x)為齒側間隙函數[5]。

將齒輪系統的傳動誤差設為s，用相對位移表示為：

聯合式（1）、（4）簡化可得：

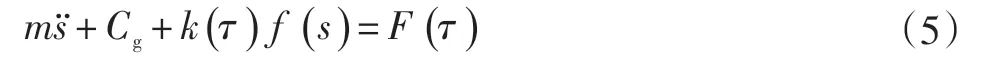
式中：齒輪副等效質量m＝m1m2/(m1＋m2)；F(τ )為系統受到的激勵。

激勵函數如下：

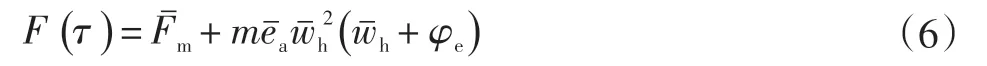
齒輪的時變嚙合剛度k(τ)是隨時間變化的周期函數，表示為傅里葉級數[6]，取一階諧波分量，則時變嚙合剛度為：

式中：k0為齒輪嚙合過程中的平均嚙合剛度；ka為齒輪系統時變嚙合剛度波動幅值；φh為初相位。

齒輪剛度與綜合嚙合誤差初始相位之間的關系為：φh＝φe＋π，將式（6）、（7）代入式（5），得到系統微分方程：

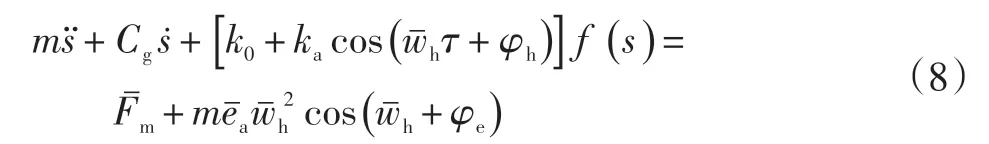
選取如下無量綱參數：

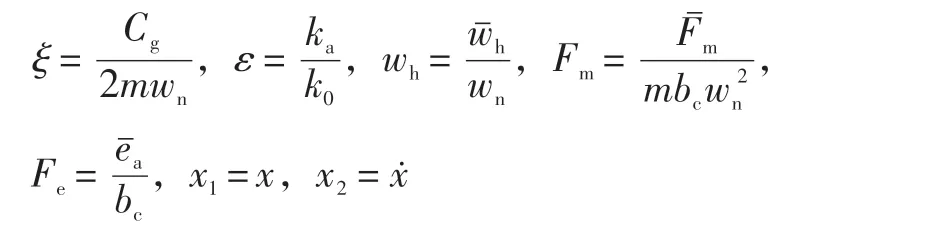
則系統微分方程的無量綱化形式為：

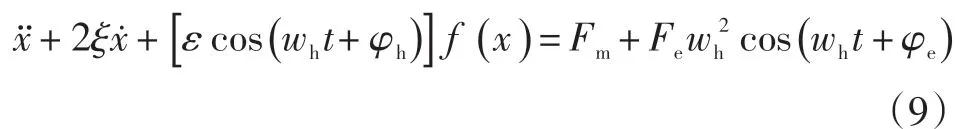
x1、x2分別表示齒輪過程中傳動誤差[7]的無量綱位移和速度，可得齒輪傳動系統的狀態方程：

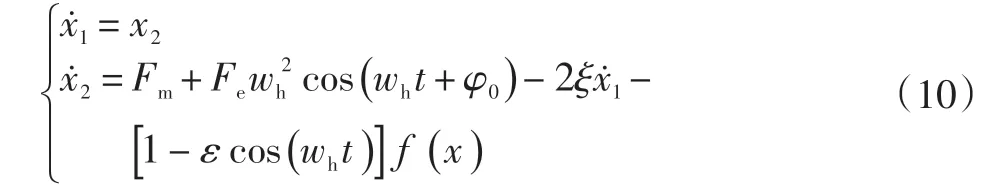
2 基于Runge－Kutta法的動力學模型分析

基于Runge－Kutta法將齒輪系統的動力學狀態方程編程，在求解過程中運用ode－45函數將齒輪系統運動微分方程中的高階方程轉化為低階方程。令Fm＝0.1，Fa＝0.2，ε＝0.1，wn＝1，同時取初始條件x1＝0、x2＝0。通過改變齒側間隙的值，得到系統在不同齒側間隙下的位移、速度圖像的分岔圖，通過分析比較，獲得齒輪在不同間隙下的動力學特性。

圖3所示為D＝1時系統隨阻尼比ξ的值變化的分叉圖，從位移圖中可以看出隨著阻尼比的增大，齒輪系統的運動狀態也會發生變化：當阻尼比ξ＜0.056時，系統運動狀態比較混亂，產生混沌運動，運動極不平穩，振動、沖擊比較大；0.056＜ξ＜0.12時，系統混沌狀態減弱，振動、沖擊減小，系統相比較ξ＜0.056的運動較平穩；ξ＝0.12時產生分岔，系統基本穩定；ξ＝0.32時系統集中為1個岔，系統開始平穩運行。

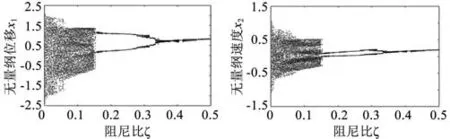
圖3 齒側間隙D＝1速度—阻尼比圖像

圖4 所示為D＝0.8時系統隨阻尼比ξ的值變化的分岔圖。隨著阻尼比的增大，齒輪系統的運動狀態發生變化：當阻尼比ξ＝0.04時，系統運動狀態比較混亂，產生混沌運動，運動極不平穩，振動、沖擊比較大；0.04＜ξ＜0.15時，系統混沌狀態減弱，振動、沖擊減小；ξ＝0.15時產生分岔；ξ＝0.33時系統集中為1個岔，系統開始平穩運行。

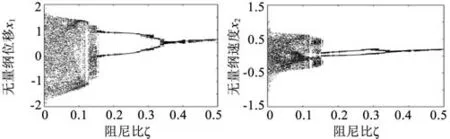
圖4 齒側間隙D＝0.8時速度—阻尼比圖像

圖5 所示為D＝0.5時系統隨阻尼比ξ的值變化的分岔圖，隨著阻尼比的增大，齒輪系統的運動狀態發生變化：當阻尼比ξ＜0.035時，系統運動狀態比較混亂，產生混沌運動，運動極不平穩，振動、沖擊比較大；0.035＜ξ＜0.18時，系統混沌狀態減弱，振動、沖擊減小；當ξ＝0.34時系統產生2個分岔，系統基本穩定；ξ＝0.39時系統集中為1個岔，系統開始平穩運行。

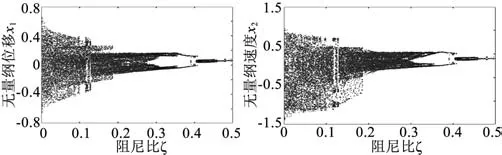
圖5 齒側間隙D＝0.5時速度—阻尼比圖像

圖6所示為D＝0.2時系統隨阻尼比ξ的值變化的分岔圖，隨著阻尼比的增大，齒輪系統的運動狀態發生變化：當阻尼比ξ＜0.08時，系統運動狀態比較混亂，產生混沌運動，運動極不平穩，振動、沖擊比較大；0.08＜ξ＜0.13時，系統混沌狀態減弱，振動、沖擊減小；ξ＝0.15時系統集中為1個岔，系統開始平穩運行。

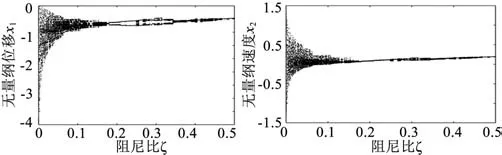
圖6 齒側間隙D＝0.2時速度—阻尼比圖像

再利用齒側間隙值為定值時，通過改變阻尼比的值來分析系統的穩定性，當齒側間隙值為1時，改變阻尼比ξ的值得到系統的運動相圖如圖7所示。

圖7 不同阻尼比下齒輪運動相圖

圖中，當齒側間隙為定值時，齒輪系統隨著阻尼比ξ的不斷增大，齒輪系統的運動狀態也在不斷的改變，阻尼比很小時，系統處于混沌狀態，系統的沖擊、振動極大，系統處于極不穩定狀態。隨著阻尼比的增大，系統的混沌狀態逐漸減弱，振動、沖擊較小，系統逐漸趨于平穩；當系統的阻尼比增大到一定值時，系統的混沌狀態基本消失，齒輪系統的運動和沖擊都較小，系統趨于穩定的運動狀態。

綜上所述，當齒輪的齒側間隙為定值時，齒輪系統在剛進入嚙合時不穩定，在某一個瞬間會達到非常不穩定的狀態，隨著時間的推移在齒輪系統會在某一時刻處于穩定運轉的狀態。當齒輪系統的齒側間隙不斷增大時，齒輪系統的沖擊也會隨著齒側間隙的增大而變大，系統的混沌狀態也就越嚴重。

3 結束語

本文通過對特種汽車輪邊減速系統齒輪傳動力學特性分析得出以下結論。

（1）隨齒輪系統的齒側間隙不斷增大，齒輪系統的沖擊變大，系統的混沌狀態也就越嚴重；

（2）當齒輪的齒側間隙為定值時，齒輪系統在剛進入嚙合時不穩定，在某一個瞬間會達到非常不穩定的狀態，隨著時間的推移在齒輪系統會在某一時刻處于穩定運轉的狀態；

（3）隨阻尼比的增大，系統逐漸趨于平穩，系統的混沌狀態基本消失，齒輪系統的運動狀態趨于穩定。