雙氣門配氣機構布置方法的應用與測試研究

劉芳,楊連亞

（安徽航瑞航空動力裝備有限公司,安徽蕪湖 241000）

0 引言

發動機配氣機構是定時開啟和關閉氣門，使新鮮的可燃混合氣或空氣得以及時進入氣缸，廢氣得以及時從氣缸排出的一種機構，是發動機中重要且復雜的部件之一。而柴油機雙氣門的配氣機構較單氣門來說，增加了氣門橋結構，系統變得更加復雜，試驗證明，若配氣機構尺寸布置不當，會導致整個系統的運行不穩定，降低系統零部件的壽命及發動機的性能，造成氣門橋磨損、導管偏磨、氣門傾斜、燃燒室內渦流混亂、進排氣不暢等。因此對于雙氣門的柴油機配氣系統的設計尤為重要。

本文提供了一種發動機雙氣門配氣機構布置方法，以運動學為理論基礎，建立配氣系統布置設計模型，進行發動機配氣機構運動特性的解析[1-2]，并以某活塞發動機的配氣機構為案例，使用本文提出的雙氣門配氣機構布置方案并結合運動學解析及動力學測試與原方案進行了對比，對比結果顯示本文所提出的方案要優于原方案。

1 分析方法構建

1.1 雙氣門配氣機構布置

雙氣門配氣機構包括雙氣門、凸輪軸、挺柱、氣門橋、推桿和搖臂，搖臂包括與氣門橋連接的第一臂部和與推桿連接的第二臂部，雙氣門是指設置兩個氣門，兩個氣門的軸線相平行，氣門橋與兩個氣門相連接，搖臂為可旋轉的設置于發動機缸蓋上，搖臂的一端與推桿相連接，搖臂的另一端與氣門橋相連接，氣門橋是用于將搖臂的運動規律傳遞給兩個氣門，推桿位于搖臂的下方，推桿與挺柱相配合，且挺柱位于推桿和凸輪軸之間，挺柱與凸輪軸相接觸，如圖1所示。

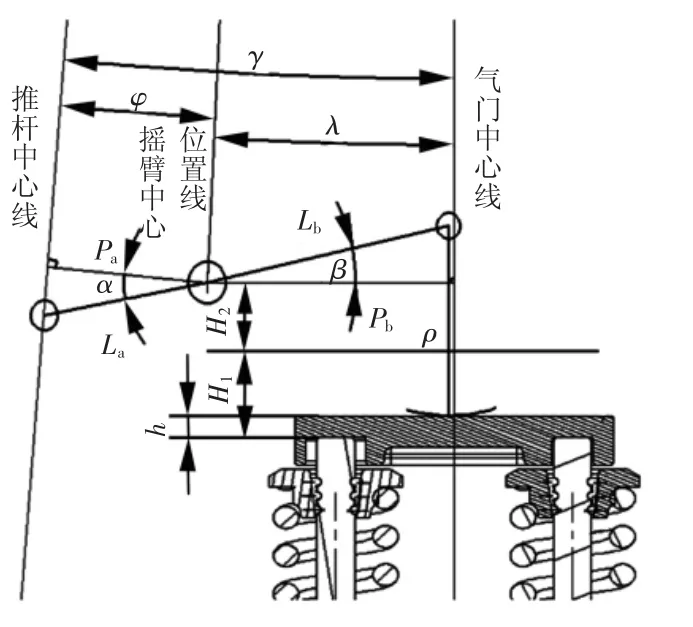
圖1 雙氣門配氣機構布置簡圖

1.2 數學模型的建立

根據圖1下置式配氣機構的布置圖，本文發動機雙氣門配氣機構布置方法包括如下步驟：1）確定雙氣門和凸輪軸的位置；2）確定氣門中心線與推桿中心線之間的初始夾角γ；3）確定搖臂的旋轉中心位置線；4）設定搖臂的旋轉中心與缸蓋的上表面之間的距離H2；5）計算搖臂的旋轉中心與氣門中心線之間的垂直距離Pb及搖臂的旋轉中心與推桿中心線之間的垂直距離Pa；6）計算搖臂與氣門橋的運動軌跡及相對滑移速度；7）確定搖臂的第一臂部的長度Lb及角度β；8）評估計算結果是否滿足預期設計指標，如果不滿足，重新執行步驟3）～步驟8），直到滿足預期設計指標；9）計算搖臂的第二臂部的長度La及角度βv；10）最終確定各零件的尺寸及位置關系。

根據步驟1）所述，首先根據發動機的氣道設計及布置空間，先確定雙氣門的位置及凸輪軸的位置。

在上述步驟2）中，根據推桿的可布置空間確定氣門中心線與推桿中心線之間的初始夾角γ，以推桿與氣門運動方向相交為負，反之為正。

在上述步驟3）中，根據初始搖臂比R0的大小，一般經驗值取1.5～1.7，通過解析方法計算出搖臂的旋轉中心位置線的位置。

a.當γ≠0時，則有

式中：λ為搖臂的旋轉中心位置線與氣門中心線之間的夾角；φ為搖臂的旋轉中心位置線與推桿中心線之間的夾角，γ=λ+φ,φ＞0，搖臂的旋轉中心位置線與氣門中心線和推桿中心線相交于一點。

通過方程求解，可以解析出初始的λ及φ值，從而可以確定搖臂旋轉中心位置線。

b.當γ=0時，則有

其中，Pa+Pb=L，L為凸輪軸的軸線到氣門中心線之間的距離。

可以解析出初始的Pa及Pb，從而可以確定搖臂旋轉中心位置線。

如圖1所示，在上述步驟5）中，

a.當γ≠0時，通過解析計算，得到：

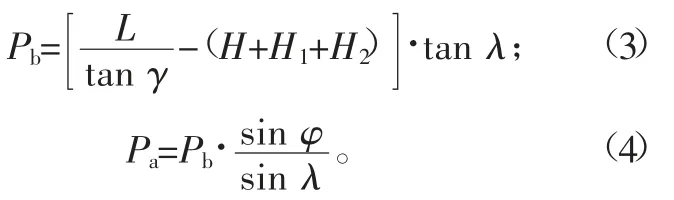
式中：H為凸輪軸到氣門桿端的距離；H1為缸蓋的上表面到氣門桿端的垂直距離；H2為缸蓋的上表面與搖臂的旋轉中心的垂直距離；

b.當γ＝0時，見公式（2）。

在上述步驟6）中，根據運動學關系，得出

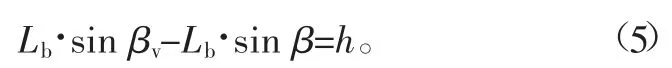
氣門橋上與搖臂的第一臂部的端面（也即搖臂的第一端的端面）相接觸的第一接觸點的位移為

式中：h為氣門的升程函數；β為氣門開啟過程中任一瞬時的位置角（即搖臂的第一臂部的長度方向和搖臂的旋轉中心與氣門中心線的垂線之間的任一瞬時的位置角）；βv為當凸輪軸凸輪的基圓部的外圓面與挺柱接觸時搖臂的第一臂部的長度方向和搖臂的旋轉中心與氣門中心線的垂線之間的位置角。

a.當搖臂的第一臂部上與氣門橋相接觸的端面為圓弧面（也即搖臂的第一端的端面為圓弧面）時，搖臂的第一臂部的端面與氣門橋的相對滑移速度為

式中：θ為凸輪軸轉角；Δs為第二觸點的位移；Δx為第一觸點的位移。

第一接觸點為氣門橋頂面上的一點，第二接觸點為搖臂的第一臂部的圓弧面上的一點，第二接觸點與氣門橋相接觸，繼而，

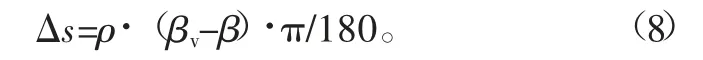
其中，ρ為搖臂的第一臂部的圓弧面的半徑。

進一步，對式（5）求導，得出

式中：θ為凸輪軸轉角；Vh為氣門的速度。

對式（6）、式（8）求導，得出：

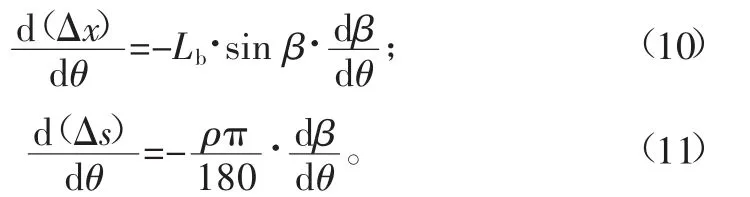
將式（10）、式（11）代入式（7），得

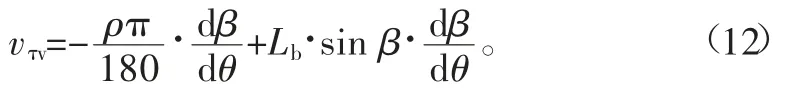
將式（9）代入式（12），得

進一步，可以求出滑移中心（在搖臂每次向下或向上擺動過程中，第一臂部相對于氣門橋進行滑動，第二接觸點具有一個起點位置和一個終點位置，第二接觸點的起點位置和終點位置的連線的中點即為滑移中心）到氣門中心線的距離P為

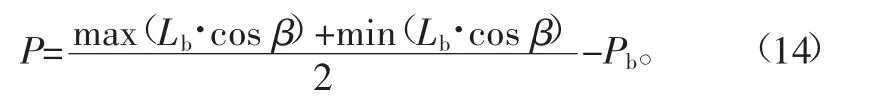
為使雙氣門的每一個氣門升程盡可能一致，氣門橋上的受力點盡可能不要偏離氣門中心線過多。因此，接觸點在氣門橋上的移動范圍宜對稱于氣門中心線，故P盡可能接近0。為了減少搖臂的第一臂部上與氣門橋相接觸的端面與氣門橋的磨損，盡量降低滑移速度。

b.當搖臂氣門側配有象腳結構時，象腳與氣門橋的滑移速度為

滑移中心到氣門中心線的距離根據式（14）計算。

在上述步驟7）中，根據步驟6）的計算結果，確定搖臂的第一臂部的長度Lb及角度β。

在上述步驟8）中，根據發動機的布置空間，調整參數，使得結果最優化。

在上述步驟9）中，計算搖臂的第二臂部的長度La及角度βv；由于推桿的中心線可能與挺柱的中心線不同心，故根據挺柱的位置及尺寸，結合步驟8）的結果，計算出推桿的最終長度及位置角度。

在上述步驟10）中，根據步驟8）及9）的結果，最終確定各零件的尺寸及位置關系，畫出配氣機構的布置圖。

2 應用實例

在配氣機構前期設計中，設計師一般都是參考比較成熟的產品，加以修改，或根據發動機的布置空間進行配氣機構的尺寸布置，然后通過運動學和動力學仿真對配氣系統進行設計校核[3-6]，對于設計完成的機構布置是否合理，并沒有一定的指標去判斷，最后通過后期的動力學試驗及可靠性試驗[7-9]，不斷對機構進行調整，直到滿足要求，這樣不僅設計周期長，而且設計成本大大增加。本文以某活塞發動機為例，用前文提出的方法對配氣機構進行優化。

2.1 發動機配氣機構原方案的分析

某兩缸柴油機采用下置式配氣機構，且進排氣側為同一布置，搖臂與氣門橋接觸面為pad面（圓弧面），如圖2所示。

圖2 配氣機構示意圖

2.1.1 原方案布置校核計算

圖2為某兩缸柴油機配氣機構示意圖，根據氣門的運動學升程及配氣機構的部分參數（如表1），對原配氣機構方案進行部分解析。

表1 原配氣機構部分參數表

通過解析得到搖臂與氣門橋接觸點的滑移軌跡及滑移速度，結果如圖3所示。

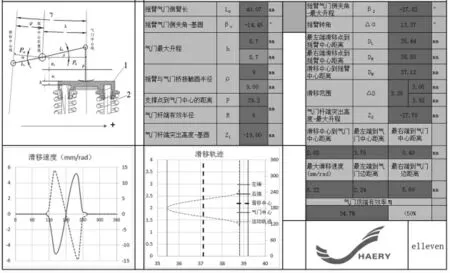
圖3 原方案計算結果

計算結果表明：搖臂與氣門橋接觸點的運動學滑移軌跡分布不合理，偏向氣門橋的一側，滑移中心離氣門的中心有2.08 mm，在高速下，由于搖臂與氣門橋是線面接觸，會引發氣門橋在運動過程中有較大角度的傾斜；最大運動學滑移速度為5.22 mm/rad，明顯偏大，會加劇氣門搖臂及氣門橋的磨損。

2.1.2 原方案動力學測試

對原柴油機配氣機構方案開展升速動力學測試。發動機缸體缸蓋安裝在配氣機構測試系統的臺架上[10-12]。變頻電動機通過傳動軸聯接配氣機構的凸輪軸，發動機缸蓋水平放置，氣門水平運動，易于布置激光傳感器[13-15]，如圖4所示。

圖4 V型兩缸柴油機的單缸動力學測試圖

本實驗凸輪軸轉速從500 r/min開始，以100 r/min為步長，逐漸增大至凸輪軸最大轉速1600 r/min，圖5為1600 r/min轉速下的進排氣動力學氣門升程曲線圖。從圖中可以看出，進排氣側氣門升程一致性較差，氣門升程的相位相差10°，最大值相差1 mm（其中in1為靠近推桿的氣門升程，以此類推）。這將對發動機性能、油耗及排放一致性有較大影響。因此此配氣機構的布置須優化。

圖5 原方案動力學氣門升程曲線圖

2.2 搖臂的優化分析

原方案配氣機構布置不合理，搖臂與氣門橋的接觸點滑移軌跡偏向一側，且離氣門中心較遠，導致氣門橋在運動過程中有較大傾斜。基于配氣機構零部件較多，重新布置周期較長，因此優化方向考慮改變搖臂氣門側的尺寸。

2.2.1 優化搖臂匹配計算

保持原有的總體布置不變，僅改變搖臂氣門側的長度及初始角度βv。計算得到的優化方案如圖6所示。與圖3的原方案對比可知：搖臂與氣門橋的接觸點滑移中心與氣門的中心基本重合；氣門的滑移范圍縮短到原來的7.4%；最大滑移速度降到原來的14%。故優化搖臂氣門側長度為39.3 mm，初始角βv為6.2°。

圖6 優化方案計算結果

2.2.2 優化方案的動力學測試

圖7為其配氣機構動力學氣門升程圖。從圖中可以看出，進排氣動力學氣門升程一致性較原方案有了較高的提升，除去凸輪桃尖附近及緩沖段有較小差別外，其他的位置基本能重合。

圖7 優化方案動力學氣門升程曲線圖

3 結論

1）通過分析配氣機構的運動學關系，提出了一種配氣機構布置設計的方法。

2）配氣機構的動態特性最終需要通過動力學測試驗證。本文試驗證明：通過仿真得到的優化方案可以有效地改善雙氣門的動態特性，提高了氣門的一致性；將氣門動態升程控制在可接受范圍內。