基于ADAMS的封閉差動行星輪系均載特性分析

潘思言 ，王文婷 ，李佳冀 ，李龍亮

（1.中國船舶集團有限公司 第七〇三研究所，哈爾濱 150036；2.南京航空航天大學 機電學院，南京 210016）

0 引言

封閉行星輪傳動在多條路徑上傳遞功率，其結構比較復雜，振動和噪聲的問題嚴重影響系統的傳動性能和壽命。各行星輪不均載問題是造成行星傳動系統振動的主要因素[1]?；贏DAMS的行星傳動的動力學分析，國內外學者均做了一系列的研究。孫宏[2]基于ADAMS建立了風電用多級行星齒輪箱虛擬樣機仿真模型，分析了系統的均載特性。李強軍[3]基于ADAMS對車用行星齒輪減速器建立了多體動力學的分析模型，研究了系統的固有頻率和振型，對系統的動態嚙合力進行對比分析。江志祥[4]建立了行星齒輪傳動系統的虛擬樣機仿真模型，基于ADAMS分析了系統的均載特性。K.M.Kang等[5]基于ADAMS分析了系統的各種安裝誤差對均載特性的影響。

國內外學者基于ADAMS對單級行星齒輪傳動系統均載特性做了較多的研究。但針對復雜的封閉差動行星輪系，基于ADAMS開展均載特性研究，鮮見文獻報道。本文研究的大功率高速重載人字齒封閉行星輪系傳動簡圖如圖1所示[6-7]。

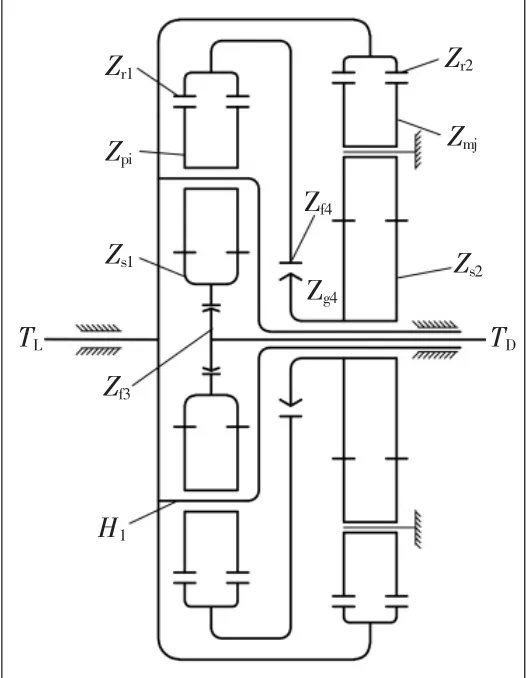
圖1 封閉行星輪系傳動簡圖

封閉差動行星輪系由封閉級和差動級組成，圖1中各構件說明如表1所示。

表1 構件符號說明

一級太陽輪Zs1輸入功率分為兩路傳動，其中一路由一級行星架H1輸出，另一路由一級內齒圈Zr1分流到二級太陽輪Zs2，再由二級內齒圈Zr2輸出，最后匯流后輸出給負載TL。

封閉差動行星齒輪傳動系統的基本參數如表2所示[1]。

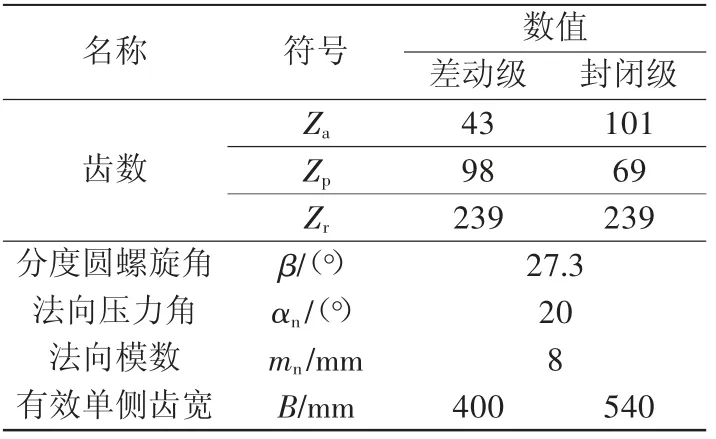
表2 封閉行星齒輪傳動系統的基本參數

1 封閉差動行星輪系虛擬裝配

一般行星輪設計為均布在太陽輪和內齒輪之間，如圖2所示。

圖2中裝配平面是指通過中心輪軸線，平分各輪齒或齒槽的平面，中心輪和裝配平面初始化后的位置依據行星輪齒數的奇偶不同而不同。其中圖2（a）為行星輪為奇數，圖2（b）為行星輪為偶數。中心輪位置經過初始化后，在裝配平面上裝入行星輪，奇數齒和偶數齒的行星輪在裝配平面上的裝配方法大致相同，此處僅以偶數齒行星輪為例闡述其裝配原理，原理圖如圖3所示。

圖2 中心輪位置初始化

中心輪經位置初始化后先在裝配平面上裝入第一個行星輪，首先調整行星輪的角度，使裝配平面平分其最上端齒槽和最下端齒槽（奇數齒時裝配平面平分最上端齒槽和最下端輪齒），然后在裝配平面上裝入第一個行星輪，如圖3（a）所示，然后再依次裝入第2、3、...i（i=2、3...n，n為行星輪個數）個。在裝入第i個行星輪時，需要將第一個行星輪逆時針方向轉動φi角度，然后在最開始裝配第一個行星輪時的裝配平面上裝配第i個行星輪，直到完成所有行星輪裝配，若第一個行星輪和第i個行星輪之間存在相位差，還需將第i個行星輪繞其自身的軸線旋轉一個相位角。

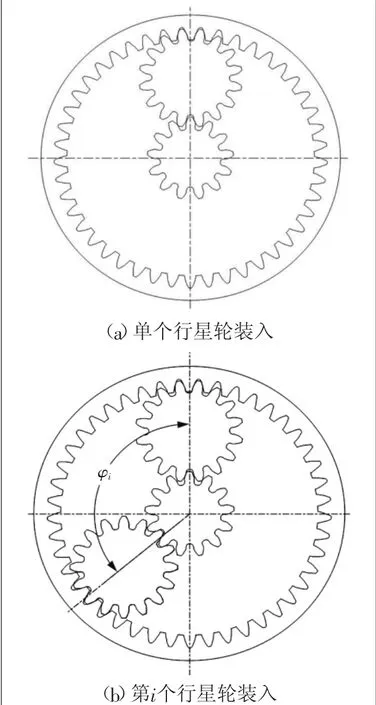
圖3 行星輪安裝

采用表1中的封閉差動行星輪系各齒輪設計參數，在UG中建模，并參照上述裝配原理對封閉差動行星輪系進行虛擬裝配，裝配圖如圖4所示。

圖4 封閉差動行星輪系裝配圖

2 封閉差動行星輪系ADAMS虛擬樣機模型

將裝配好行星輪系的三維模型導入ADAMS中。采用parasolid數據接口，模型導入后，建立虛擬樣機模型，這里，采用接觸副近似代替齒輪副分析齒輪嚙合。

將裝配好的封閉差動行星輪系導入ADAMS中，施加約束如下：1）各轉動件之間均施加轉動副；2）各接觸齒對之間均施加接觸副；3）輸入軸上施加驅動力矩，輸出軸上施加負載力矩。

完成各構件之間的約束，以及輸入力矩輸出力矩的添加之后，建立的虛擬樣機模型如圖5所示。

圖5 ADAMS虛擬樣機模型

3 仿真對比分析

3.1 運動學仿真對比分析

通過對系統進行運動學仿真，可以在產品設計之初通過檢查各構件的運動情況，來判斷產品設計方案及設計參數的可行性，可大大提高產品的開發效率。

圖6、圖7分別為輸入轉速在2955 r/min，仿真時間為3 s，仿真步數為10 000步的工況下差動級和封閉級各行星輪質心運動軌跡。

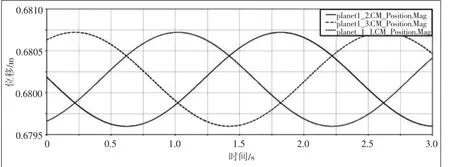
圖6 差動級行星輪質心運動軌跡

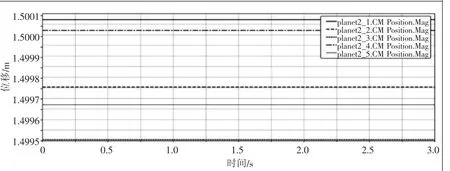
圖7 封閉級行星輪質心運動軌跡

由圖7可知，差動級各行星輪質心運動軌跡呈平滑的周期性波動，封閉級各行星輪軌跡呈直線變化，主要是因為差動級行星架轉動、封閉級行星架固定而造成的。從封閉級和差動級質心運動軌跡可以看出，系統傳動平穩，無嚙合干涉、沖擊現象，驗證了該虛擬樣機模型的可行性。

圖8為仿真得出的系統傳動比，為系統輸出轉速和輸入轉速之比。

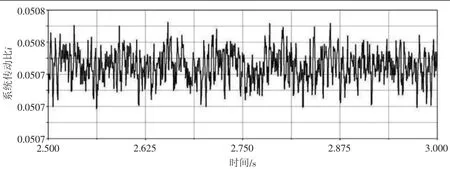
圖8 系統仿真傳動比

由圖8可知，在整個運轉過程中，系統傳動比在0.0507上下存在微小的波動，主要是由于齒輪嚙合過程中其嚙合剛度的時變性導致了傳動比的微小波動，這與齒輪實際運轉狀況相符合。

3.2 動力學仿真對比分析

因為ADAMS中無法直接測量系統的均載系數，需要在系統中建立自定義測量函數，封閉差動行星輪系的均載系數計算方法為：

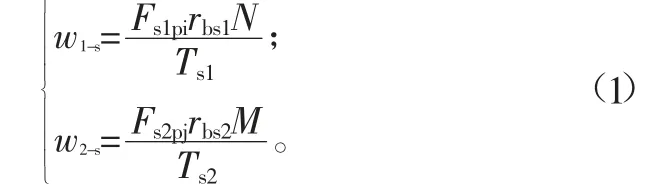
式中：w1-s、w2-s、Fs1pi、Fs2pj、Ts1、Ts2分別為基于ADAMS仿真得出的差動級和封閉級均載系數、太陽輪和行星輪之間的動態嚙合力、太陽輪上的輸入轉矩；rbs1、rbs2、N、M分別為差動級和封閉級太陽輪基圓半徑、差動級和封閉級行星輪個數。

圖9、圖10分別為輸入功率為20 000 kW，輸入轉速為2955 r/min工況下系統仿真得出的封閉級和差動級均載系數。

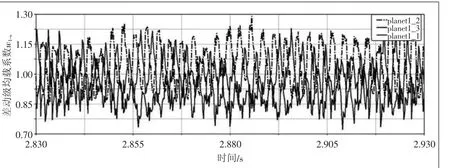
圖9 基于ADAMS仿真的差動級均載系數

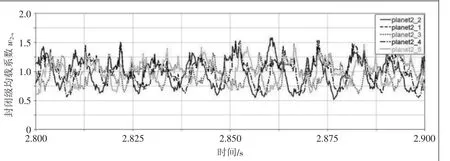
圖10 基于ADAMS仿真的封閉級均載系數

由圖可知，基于ADAMS仿真的差動級均載系數最大值約為1.3，封閉級均載系數最大值約為1.58，理論計算的差動級均載系數最大值為1.39，封閉級均載系數最大值為1.2，兩者之間的相對誤差如表3所示。

表3 仿真均載系數值與理論計算值對比

通過上述動力學仿真并與理論計算值對比可知，仿真得到的效率值及均載系數與理論計算數值均存在一定的誤差，且封閉級均載系數誤差較大，但兩者效率值及均載系數相對誤差均在允許范圍之內，這也一定程度上驗證了理論模型及理論計算的可靠性。兩者之間的誤差主要有以下幾點原因：

1）理論模型和虛擬樣機模型都做了相應的簡化，但理論模型簡化是為了便于數學建模及計算，虛擬樣機模型的簡化是為了便于三維實體建模及裝配，兩者模型簡化的側重點不同，使得兩模型存在一定的差別。

2）理論模型和虛擬樣機模型采用的摩擦因數模型不同，前者采用基于彈流潤滑理論的摩擦因數模型，后者采用ADAMS中自帶的庫倫摩擦模型。

3）對虛擬樣機進行虛擬裝配時，隨著行星輪個數的增加，裝配誤差急劇增大，使得各行星輪的載荷均勻性變差，但理論模型中各嚙合對之間均設以相同的誤差，兩者之間存在一定差別。

4 結論

本文主要運用虛擬樣機技術對封閉差動行星輪系進行動力學均載仿真分析。為了得到一個和理論模型更為接近的封閉差動行星輪系虛擬樣機模型，首先詳細地闡述了虛擬裝配理論并運用UG對各個部件進行了虛擬裝配，然后對模型中的約束進行了分析，闡述了其接觸力及接觸剛度計算方法，最后在ADAMS中建立了虛擬樣機模型。建立近似于理論模型的虛擬樣機模型后，為了驗證該模型的可行性，首先對模型做了運動學仿真，在驗證了各行星輪運轉平穩、無干涉后，又通過驗證仿真傳動比與理論計算傳動比的一致性進一步驗證了該虛擬樣機模型的可行性與可靠性。最后通過動力學仿真，得出了系統差動級、封閉級均載系數，并與理論計算值進行對比分析，研究成果可供工程設計參考。