時(shí)間分割圓弧插補(bǔ)算法的改進(jìn)

梁曉兵，劉志強(qiáng)，王璠

（河南機(jī)電職業(yè)學(xué)院，鄭州 451191）

0 引言

目前數(shù)控系統(tǒng)在插補(bǔ)圓弧的過(guò)程中，使用的基本上都是二階近似法進(jìn)行圓弧插補(bǔ)的，這種方法使用一組直線來(lái)逼近圓弧，計(jì)算出插補(bǔ)周期的坐標(biāo)增量值。目前國(guó)內(nèi)外很多學(xué)者已經(jīng)在這方面進(jìn)行了很多研究，韓賽飛等[1]實(shí)現(xiàn)了改進(jìn)型圓弧插補(bǔ)算法及FPGA實(shí)現(xiàn)；劉煥等[2]分析了基于微分模型的空間圓弧與橢圓弧插補(bǔ)算法；姚曉通等[3]分析了圓弧插補(bǔ)算法的FPGA實(shí)現(xiàn)；李偉光等[4]分析了無(wú)限直線逼近圓弧方法；劉鵬飛等[5]分析了在機(jī)器人領(lǐng)域中的應(yīng)用；何均等[6]實(shí)現(xiàn)了短線段空間圓弧轉(zhuǎn)接與插補(bǔ)；劉放等[7]介紹了基于四元數(shù)的空間圓弧插補(bǔ)算法；王中平等[8]基于矢量分析了圓弧插補(bǔ)算法；詹泳等[9]實(shí)現(xiàn)了五軸空間圓弧插補(bǔ)；朱國(guó)力等[10]介紹了插補(bǔ)算法的應(yīng)用；賀德華等[11]推導(dǎo)了空間任意圓弧的插補(bǔ)算法；高宏卿等[12]推導(dǎo)了空間圓弧變換插補(bǔ)原理與算法。

在計(jì)算過(guò)程中，傳統(tǒng)插補(bǔ)算法使用了三角函數(shù)的泰勒展開式中的低階近似，使得插補(bǔ)點(diǎn)遠(yuǎn)離圓弧，產(chǎn)生一定的累積誤差。針對(duì)這種情況，提出一種改進(jìn)的圓弧插補(bǔ)算法，進(jìn)一步提高插補(bǔ)運(yùn)算精度。

1時(shí)間分割法插補(bǔ)原理

現(xiàn)以第一象限逆時(shí)針插補(bǔ)為例，說(shuō)明傳統(tǒng)時(shí)間分割法實(shí)現(xiàn)原理。如圖1所示，設(shè)待插補(bǔ)圓弧半徑為R，圓心坐標(biāo)（0，0），插補(bǔ)速度為F，插補(bǔ)周期為T，每次插補(bǔ)的進(jìn)給步長(zhǎng)f=F·T。

圖1 圓弧逆時(shí)針插補(bǔ)兩點(diǎn)位置關(guān)系

對(duì)圓弧上動(dòng)點(diǎn)Pi（xi，yi），滿足以下關(guān)系：

yi＝R·sinα；xi＝R·cosα。

Pi＋1（xi＋1，yi＋1）是下一插補(bǔ)點(diǎn)坐標(biāo)，PiPi＋1是每插補(bǔ)周期的進(jìn)給步長(zhǎng)f，其對(duì)應(yīng)的圓心角是θ。

下一插補(bǔ)點(diǎn)坐標(biāo)值計(jì)算方法為

yi＋1＝R·sin（α＋θ）；xi＋1＝R·cos（α＋θ）。

展開后得：

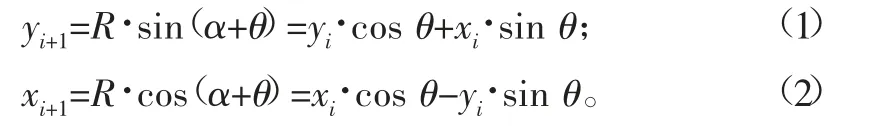
對(duì)其中的三角函數(shù)泰勒展開并取二階以下變量公式可得：

cosθ≈1－θ2/2；sinθ≈θ。

且由θ＝f/R，代入式（1）、式（2），可得：

設(shè)A＝f/R＝θ，B＝θ2/2，代入式（3）、式（4），可得：

取Δyi＝y(tǒng)i＋1－yi＝－B·yi＋A·xi；Δxi＝xi＋1－xi＝－B·xi－A·yi。

弓高誤差δ計(jì)算公式為

2 時(shí)間分割法改進(jìn)算法

上面?zhèn)鹘y(tǒng)的時(shí)間分割法圓弧插補(bǔ)運(yùn)算，引入了近似計(jì)算，存在一定的誤差，而且弓高誤差較大，為了減小誤差，下面提出一種改進(jìn)的時(shí)間分割圓弧插補(bǔ)改進(jìn)方法。

2.1 改進(jìn)算法原理

對(duì)于有一定誤差的待加工面（如圖2），如果實(shí)際加工面位于理論待加工面單側(cè)，那么最大誤差就是實(shí)際加工最大尺寸減去理論加工面尺寸。如果實(shí)際加工面位于理論待加工面兩側(cè)，那么，最大誤差就是理論面和實(shí)際面兩側(cè)尺寸差的最大值，如果兩面對(duì)稱，最大誤差就是實(shí)際誤差的一半。

圖2 待加工面

2.2 算法實(shí)現(xiàn)

對(duì)于給定的弓高誤差δ和圓弧半徑R，分別做半徑為R-δ/2、R+δ/2圓弧，已知Pi（xi，yi）點(diǎn)，求下一插補(bǔ)點(diǎn)Pi+1（xi+1，yi+1）坐標(biāo)。過(guò)Pi點(diǎn)做內(nèi)圓弧的切線交半徑為R-δ/2內(nèi)圓弧于切點(diǎn)P（xq，yq）點(diǎn)，如圖3所示。

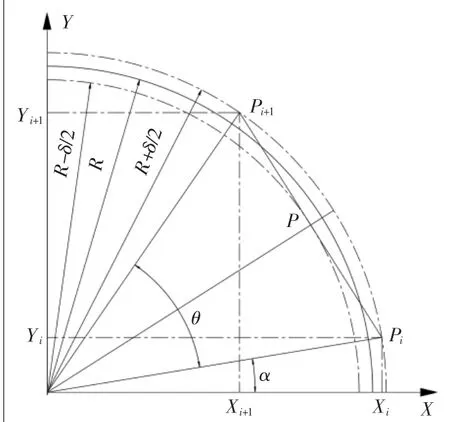
圖3 改進(jìn)算法逆時(shí)針插補(bǔ)點(diǎn)位置關(guān)系

由于P點(diǎn)是切點(diǎn)，PPi是內(nèi)圓弧切線，且PPi長(zhǎng)度值為f/2，由幾何關(guān)系可得：

代入式（10）、式（11），可以求得P（xq，yq）坐標(biāo)為：

根據(jù)圖3幾何關(guān)系，P（xq，yq）為Pi（xi，yi）點(diǎn)和Pi+1（xi+1，yi+1）連線的中點(diǎn)，可知：

聯(lián)立式（12）～式（15），可得：

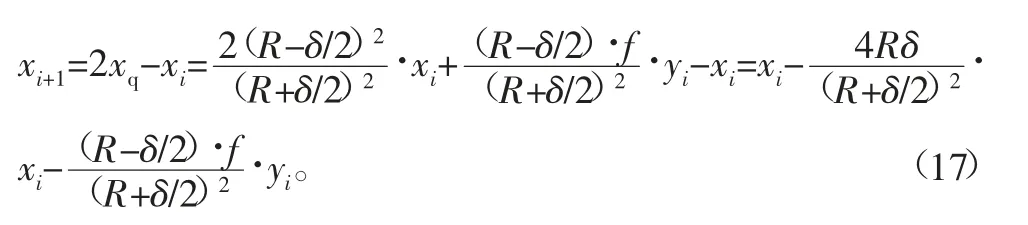
Δyi=yi+1-yi，Δxi=xi+1-xi，改進(jìn)后的時(shí)間分割圓弧插補(bǔ)算法的計(jì)算步驟如下。

2.3 特殊點(diǎn)處理

由于上面為了減小誤差，改進(jìn)了算法，計(jì)算過(guò)程中插補(bǔ)的點(diǎn)都在半徑為R+δ/2圓弧上，由此引入了2個(gè)特殊點(diǎn)即起點(diǎn)P0（x0，y0）和終點(diǎn)Pe（xe，ye），這兩個(gè)特殊點(diǎn)需要特殊處理。

對(duì)于起點(diǎn)P0（x0，y0），給定的起點(diǎn)坐標(biāo)位于半徑為R的圓弧上，實(shí)際插補(bǔ)計(jì)算的起點(diǎn)位于半徑為R+δ/2的圓弧上，因此需要計(jì)算插補(bǔ)起點(diǎn)Pc0（xc0，yc0）。

根據(jù)圖3幾何關(guān)系得：

對(duì)于終點(diǎn)坐標(biāo)Pe（xe，ye），實(shí)際需要的終點(diǎn)坐標(biāo)位于半徑為R圓弧上，實(shí)時(shí)插補(bǔ)計(jì)算的終點(diǎn)位于半徑為R+δ/2圓弧上，因此需要計(jì)算實(shí)際終點(diǎn)Pea（xea，yea）。根據(jù)圖3的幾何關(guān)系可得：

3 兩種算法比較分析

在傳統(tǒng)算法中，由于對(duì)正弦余弦三角函數(shù)進(jìn)行了二階近似，由式（5）、式（6）求得的下一插補(bǔ)點(diǎn)可能會(huì)偏離圓弧產(chǎn)生徑向誤差。插補(bǔ)過(guò)程中由于使用了弦線代替圓弧，還會(huì)產(chǎn)生弓高誤差。

在改進(jìn)算法中，由于使用R+δ/2的圓弧代替半徑為R的圓弧，同樣會(huì)產(chǎn)生徑向誤差和弓高誤差。

3.1 徑向誤差

徑向誤差即實(shí)際插補(bǔ)點(diǎn)坐標(biāo)與理論坐標(biāo)點(diǎn)的偏差，實(shí)際計(jì)算根據(jù)實(shí)際插補(bǔ)點(diǎn)坐標(biāo)的坐標(biāo)值與理論半徑的距離來(lái)表示：

由式（5）、式（6）可得傳統(tǒng)插補(bǔ)算法徑向誤差為

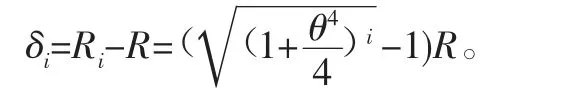
由于θ不為0，δci也不等于0，即存在徑向誤差，而且隨著插補(bǔ)次數(shù)的增加，徑向誤差也會(huì)越來(lái)越大。

對(duì)于改進(jìn)后的算法，由圖3幾何關(guān)系得

由式（16）、式（17）、式（19）得

代入式（18），可得

經(jīng)過(guò)改進(jìn)后，算法誤差是恒定值，和插補(bǔ)次數(shù)無(wú)關(guān)，誤差不累計(jì)，可以在預(yù)插補(bǔ)階段進(jìn)行誤差補(bǔ)償一個(gè)恒定值，進(jìn)一步減小誤差。

3.2 弓高誤差

3.3 插補(bǔ)速度

在傳統(tǒng)得插補(bǔ)算法中，使用了二階近似來(lái)簡(jiǎn)化計(jì)算過(guò)程，改進(jìn)算法沒(méi)有采用近似處理，一方面是因?yàn)楝F(xiàn)在嵌入式系統(tǒng)計(jì)算能力越來(lái)越強(qiáng)，比如STM32等微控制器都帶了硬件除法器；另一方面是因?yàn)楸靖倪M(jìn)算法在插補(bǔ)過(guò)程中和傳統(tǒng)插補(bǔ)算法過(guò)程一樣，除了常量系數(shù)計(jì)算不一樣，常量系數(shù)計(jì)算過(guò)程可以放到插補(bǔ)預(yù)處理階段進(jìn)行，而且改進(jìn)算法比傳統(tǒng)算法只多了一步除法運(yùn)算。在168 MHz的STM32f407芯片上進(jìn)行插補(bǔ)系數(shù)計(jì)算仿真，結(jié)果測(cè)得傳統(tǒng)算法每次實(shí)際計(jì)算時(shí)間為0.148μs，改進(jìn)后插補(bǔ)時(shí)間為0.369μs，時(shí)間基本一致。

綜上，傳統(tǒng)算法徑向誤差隨插補(bǔ)次數(shù)的增加不斷增加，改進(jìn)算法后，徑向誤差不隨插補(bǔ)次數(shù)變化而變化，穩(wěn)定無(wú)變化。弓高誤差傳統(tǒng)算法為f2/(8R)，改進(jìn)后算法誤差為f2/(16R)，只是傳統(tǒng)算法誤差的一半。由于徑向誤差和弓高誤差在相反方向，最大誤差為徑向誤差和弓高誤差的最大值。改進(jìn)后算法最大誤差為f2/(16R)，只是傳統(tǒng)算法誤差的一半。

4 結(jié)語(yǔ)

通過(guò)對(duì)時(shí)間分割圓弧插補(bǔ)算法和改進(jìn)后的算法對(duì)比計(jì)算分析，可知改進(jìn)算法的誤差要比原來(lái)的算法誤差減小一半，精度得到了很大提高。改進(jìn)后插補(bǔ)過(guò)程運(yùn)算速度相同，插補(bǔ)系數(shù)計(jì)算相對(duì)低一些，但是誤差不到1μs，滿足實(shí)時(shí)插補(bǔ)要求。