基于有限元法帶邊型聲子晶體結構的帶隙研究

鄧微，陳曉宏

（廣州鐵路職業技術學院,廣州 510430）

0 引言

聲子晶體[1]可分為Bragg和局域共振聲子晶體兩種不同結構形式，通過局域共振結構帶隙產生的機理分析，在有限的空間里，只有用小于波長兩個數量級的周期性結構才能在低頻段產生帶隙，即“小尺寸控制大波長”。本文通過在單層板上敷設等效“質量-彈簧”的局域共振子，獲取較低的帶隙起始頻率和較寬的帶隙絕對寬度，從而實現對500 Hz下的低頻振動及噪聲進行減振降噪控制。

1 帶邊型局域共振模型及材料參數

為研究單層板上添加局域共振子對低頻振動特性的影響，建立合適的單板板附加共振子模型結構，如圖1所示,其中晶格常數邊長a=0.2 m，厚h為0.0025 m，軟體層（橡膠阻尼塊）A半徑r2=0.05 m,厚度a2為0.01 m，具體參數如表1所示。圖1是kx、ky方向完全對稱的正方晶格，周期結構的第一和不可約布里淵區可用（如圖2陰影部分）表示。

圖1 帶邊型模型

圖2 正方晶格

表1 局域振子材料

2 彈性波帶隙計算

選擇有限元法[2]對聲子晶體的帶隙特性進行研究。對聲子晶體原胞結構進行參數設置、網格劃分施加相應邊界條件對結構進行后處理，就能得到特征頻率和波矢之間的能帶關系圖。

2.1 有限元法及Bloch原理

對二維周期結構進行有限元法求解，特征值方程為

式中：K、M分別為周期共振子結構的剛度、質量矩陣；U為原胞結構的特征向量；ω為角頻率。

根據布洛赫（Bloch）定理[3]，沿x、y二維方向周期性結構位移場方程為

式中：K′、M′分別為二維周期共振子結構的剛度、質量矩陣；μ為波矢；μx、μy滿足x、y二維方向周期性條件。

2.2 有限元法能帶計算

利用有限元法沿x、y方向對波矢（k）布里淵區邊界進行周期性掃描，選擇Floquet周期性邊界條件，在（-π/a,π/a）范圍進行掃描。選取前10階特征頻率進行分析，可得到沿x、y方向周期性方向的能帶結構圖（如圖3）和高對稱點圖（如圖4）。

圖3 二維聲子結構能帶結構圖

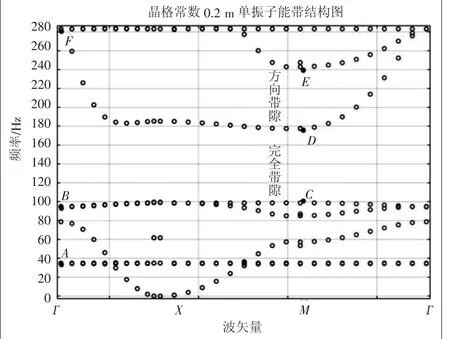
圖4 能帶結構圖的高對稱點

在能帶結構圖中的高對稱點（A～F）進行標記，并結合原胞的振動模態逐一分析其位移振型。

分析圖3，存在三條平直模式能帶、一段完全帶隙及一個區域的方向帶隙。分析單振子位移振型圖,如圖5（a）～圖5（f）,在A點模態39 Hz附近，在局域共振子內部形成一個旋轉模態，振子中心形成一個繞z軸呈渦輪狀的體位移，由于共振子未能與基體板件中的能量波進行耦合作用，色散能帶上所有的能量均能在板內進行自由傳播從而形成通帶。在B、C點99 Hz附近，共振子和基板內的lamb波相互作用，使縱向平面內平移模態產生的水平剪切波和面外橫向模態產生的彎曲波相互作用形成一個剪切模態抑制z方向的扭轉模態振動，致使質量塊（B）沿垂直方向產生剪切形變，產生z方向的垂向力分量給基體板，同樣此時的軟體層（A）橡膠阻尼起剛度彈簧的作用產生諧振從而打開禁帶形成帶隙的下邊界。在D點180 Hz頻率處，質量體（B）沿垂直方向施加給基板產生一個垂向力抑制局域聲子板中的彎曲波橫向彎曲振動，引起共振子和基體板件之間反相振動，此時產生的垂向力致軟體層橡膠阻尼等效為受壓的彈簧裝置，產生形變消耗彎曲波的內部能量，截斷帶隙形成上邊界，故在99～180 Hz范圍內形成完全帶隙，絕對帶寬為81 Hz，如圖3在此頻率范圍內存在完全帶隙。而在180～240 Hz之間大部分區域未出現本征頻率，稱之為方向帶隙，同樣在E點的產生一個z方向的垂向力，也能對面外模態的彎曲波進行抑制。

圖5 高對稱點的振型圖

3 帶邊形局域共振帶隙優化研究

3.1 尺寸因素對單振子帶隙的影響

3.1.1 晶格尺寸（a）對單振子帶隙的影響

設置步長為0.025 m的晶格尺寸0.150、0.175、0.200、0.225 m進行分析，改變其結構參數，基體板厚度發生相應變化，但總質量維持不變，如表2所示。

表2 試件模型參數

分析圖6，根據帶隙形成原理分析，帶隙下邊界起始頻率和共振子的固有頻率相近，由于基體板和共振子的質量不變，故下邊界起始頻率維持不變。當基體板的晶格常數（a）變大時，共振子在基體板的接觸面填充率變小，上邊界的終止頻率從200 Hz向140 Hz低頻方向移動且隨邊長的增長而逐漸減小，禁帶絕對寬度變窄。

圖6 F-1600型三缸單作用泥漿泵流量曲線

圖6 晶格常數（a）改變對帶隙影響

3.1.2 質量塊B半徑（r1）對單振子帶隙的影響

為探究質量塊B半徑（r1）對其第一帶隙的影響，選取步長0.01 m，r1半徑分別設置為0.04、0.05、0.06、0.07 m尺寸，局域共振子的總質量恒定，其厚度發生改變，其結構參數如表3所示。

表3 試件模型參數

由圖7知，當質量塊B半徑r1從0.05 m減至0.04 m時，帶隙下邊界往低頻方向移動至90 Hz處,此時禁帶上邊界為155 Hz，完全帶寬縮至65 Hz。當散射體B半徑r1從0.05 m增至0.07 m時，起始頻率從100 Hz往低頻拓展至72 Hz,而帶隙截止頻率保持不變，完全帶隙寬度達到了102 Hz,在軟體層半徑和厚度不變的情形下，散色體質量塊B的半徑增大對生成帶隙的下邊界有很好的拓寬。散射體B的半徑在0.04～0.07 m的范圍內，帶隙起始頻率先往高頻移動，然后往低頻拓寬，帶隙寬度逐漸增大。其中0.05～0.07 m半徑下截止頻率保持不變。

圖7 質量塊B半徑改變對帶隙影響

3.1.3 軟體層A半徑（r2）對單振子帶隙的影響

為探究軟體層A半徑（r2）對其第一帶隙的影響，選取步長0.01 m，r2半徑分別設置為0.04、0.05、0.06、0.07 m尺寸，其總質量維持不變，而對應的厚度發生改變，結構參數如表4所示。

表4 試件模型參數

如圖8所示，軟體層A半徑為0.04 m時其起始頻率為48 Hz,截止頻率為102 Hz。隨著r2的增大，起始頻率從95 Hz單調上升增至175 Hz,截止頻率從182 Hz升至248 Hz。r2從0.04 m增至0.05 m時，其帶隙寬度拓寬增幅較0.06、0.07 m要大。從r2增大時，其在基體板水平方向往四周進行了擴寬，相當于對“彈簧”進行并聯處理。減小厚度相當于縮小對“彈簧”的串聯，致使共振子等效剛度增大。根據帶邊型共振帶隙形成機理，剛度降低使帶隙下邊界向高頻延伸，共振子與基體板之間的振動耦合作用增強，絕對帶隙寬度呈拓寬的趨勢。

圖8 軟體層A半徑改變對帶隙影響

圖8 軟體層A半徑改變對帶隙影響

3.2 材料因素對帶隙的影響

3.2.1 軟體層A彈性模量對單振子帶隙的影響

為探究軟體層A彈性模量對其第一帶隙的影響，僅改變軟體層A的彈性模量分別設置為0.1E、E、5E、10E，其他結構參數不變，如表5所示。

表5 軟體層A彈性模量改變

如圖9，設置標準彈性模量的0.1倍時（E1）時，其帶隙下邊界、帶隙上邊界分別為33、62 Hz，帶隙寬度僅有29 Hz。究其原因在共振子質量不變時，等效剛度與振子的固有頻率成正比關系,當彈簧等效剛度減小時相應的固有頻率也降低。當彈性模量降低時，使局域共振子變“軟”，其與基體板的耦合作用減弱，從而帶隙的起始頻率降低，帶隙寬度變窄。反之當彈性模量增大5倍（E3）、10倍（E4）時，軟體層A的彈性系數相應減小，共振子的等效剛度變大，共振子和基體板兩者之間的耦合作用增強，帶隙移至高頻，帶隙寬度拓寬。

圖9 軟體層A彈性模量改變對帶隙影響

3.2.2 散射體質量塊B材料密度對單振子帶隙的影響

為探究散射體質量塊B密度對其第一帶隙的影響，根據密度的大小依次選取鋁、鋼（標準）、銅、鉛等材料，其他結構參數不變，如表6所示。

表6 局域振子不同材料質量塊B

分析圖10,當質量塊為鋁件時，共振子的附加質量相比原試件降低,根據等效質量和固有頻率之間反比的關系，帶隙起始頻率移向高頻段。選用鉛質量塊時，由于質量塊密度增加，在等效質量-彈簧系統中質量比增大，結構的固有頻率降低，帶隙的起始頻率也降低，同時共振子和基體板中間的耦合作用增強，拓寬帶隙寬度，但缺點是附加的質量增大。

4 結論

本文運用參數化設計在單層板上敷設局域共振子的聲子晶體結構，分析其結構特性，利用有限元方法仿真得到500 Hz以下頻率的的帶隙分布情況。分析并優化各組成部分的結構尺寸和材料因素對帶隙形成的影響。通過分析，可以將此研究結論運用于鐵道車輛等載運設備的外殼或者地板結構，起到減振隔聲的作用。