視覺測量方法

易懷安 趙欣佳 唐 樂 陳永倫

桂林理工大學(xué)機(jī)械與控制工程學(xué)院，桂林，541006

0 引言

表面粗糙度是工件加工過程中刀具在其表面留下來的刀痕產(chǎn)生的，它是衡量機(jī)械零件的一個主要幾何精度指標(biāo)，對零件的配合性質(zhì)、耐磨性、抗腐蝕性以及密封性等會產(chǎn)生顯著的影響。傳統(tǒng)的表面粗糙度測量方法是利用觸針式測量設(shè)備，其主要工作原理是用觸針裝置的探頭劃過工件表面，并監(jiān)測探頭運(yùn)動，測量工件表面的截面高度信息。該測量方法的檢測精度受探針半徑影響較大，且不支持在線測量，效率低下。此外，當(dāng)被測工件的表面較軟時，其表面存在被探頭劃傷的風(fēng)險。為解決上述問題，一些研究者已開發(fā)了許多非接觸的光學(xué)測量設(shè)備，如白光干涉儀、原子力顯微鏡和激光顯微系統(tǒng)等。但這類測量設(shè)備由于成本高、受工作環(huán)境影響較大和測量視野較窄等原因，在一定程度上限制了其工程應(yīng)用。而機(jī)器視覺測量是基于光學(xué)成像原理的測量方法，利用工業(yè)相機(jī)采集工件的表面圖像，然后提取圖像中與表面粗糙度參數(shù)相關(guān)的特征指標(biāo)，進(jìn)而可預(yù)測已知圖像特征指標(biāo)對應(yīng)位置的表面粗糙度。該方法具備單次測量面積大、效率高、非接觸、可實(shí)現(xiàn)自動化測量、成本較低等優(yōu)點(diǎn)，近二三十年來得到了國內(nèi)外許多研究者的廣泛關(guān)注[1-3]。目前基于機(jī)器視覺測量表面粗糙度的評價指標(biāo)大多是從灰度圖像中提取相關(guān)評價指標(biāo)來表征粗糙度[4-7]，忽視了顏色信息具有信息量豐富、抗污染、測量精度高等優(yōu)點(diǎn)。針對這一問題，近年來一些研究者開展了基于顏色信息指標(biāo)對表面粗糙度進(jìn)行機(jī)器視覺測量的研究。YI等[8-9]提出基于RGB顏色空間三基色之間的色差(color difference,CD)算法與彩色圖像清晰度算法，構(gòu)建此類指標(biāo)與表面粗糙度的關(guān)系模型。LU等[10]構(gòu)造一種顏色分布統(tǒng)計矩陣來表征兩種光源在粗糙度表面形成的混疊虛擬圖像，并根據(jù)顏色分布統(tǒng)計矩陣設(shè)計純色能量指標(biāo)和混疊區(qū)域面積指標(biāo)來建立與表面粗糙度的關(guān)系模型。LIU等[11]依據(jù)光源在不同粗糙度表面形成虛像的擴(kuò)散區(qū)域不同，設(shè)計基于紅綠顏色空間的紅綠重疊指數(shù)來評價表面粗糙度。雖然這些研究相對灰度圖像都取得了不錯的實(shí)驗(yàn)結(jié)果，但彩色圖像每個像素點(diǎn)都是由紅、綠和藍(lán)三個分量按比例混合而成，它們存在一定的制約關(guān)系。如果只對圖像的某個通道單獨(dú)處理，則會破壞顏色信息的整體性，而上述顏色信息評價指標(biāo)均建立在紅、綠兩種顏色的分布差異上。此外，這些表征粗糙度的顏色信息指標(biāo)沒有基于數(shù)學(xué)意義上的合理數(shù)據(jù)結(jié)構(gòu)表達(dá)。

針對上述問題，本文提出利用四元數(shù)對彩色圖像進(jìn)行建模，充分考慮彩色圖像作為一個整體所具有的顏色信息，利用純四元數(shù)的三個虛部來分別代替彩色圖像中紅、綠和藍(lán)三個顏色通道，基于不同粗糙度表面對光的反射成像所攜帶輻射能量分布的差異，對四元數(shù)進(jìn)行奇異值分解，進(jìn)而構(gòu)造奇異值熵指標(biāo)來評價磨削表面粗糙度。

1 圖像奇異值熵評價方法機(jī)理

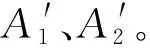
I(x，y)=f(L(x，y)，F(xiàn)(x，y)，R(x，y))

(1)

其中，照度L(x，y)表示照射在磨削表面上的光照強(qiáng)度，是單位面積上所接受可見光的能量；表面特性F(x，y)包括表面粗糙度和表面紋理方向；反射R(x，y)表示粗糙表面將光線反射到相機(jī)里的能力。對于灰度圖像，圖像質(zhì)量I(x，y)以灰度值表示；對于彩色圖像，圖像質(zhì)量I(x，y)在RGB顏色空間以紅、綠和藍(lán)三個分量值表示。因此，當(dāng)照度L(x，y)和材料表面反射R(x，y)一定時，表面特性F(x，y)則與圖像質(zhì)量I(x，y)密切相關(guān)。而本文的實(shí)驗(yàn)正是在同一種光照和材料的條件下進(jìn)行的。事實(shí)上，表面特性F(x，y)在微觀上反映了材料表面高低變化程度(即材料表面粗糙度)，故理論上可認(rèn)為RGB顏色空間的圖像質(zhì)量I(x，y)與表面特性F(x，y)存在一定的內(nèi)在聯(lián)系。

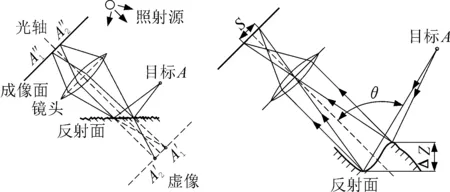
(a) 粗糙表面對成像 的影響 (b) 粗糙高度方向?qū)Τ上?的影響圖1 粗糙表面成像示意圖Fig.1 Diagram of rough surface imaging

由能量守恒定律可知，假設(shè)一束光以一定角度照射到物體表面時，若忽略金屬表面所吸收的光能量，則大部分光會被反射，但由于物體表面非理想光滑，所以一部分光會發(fā)生漫反射到空間各個方向，而反射光的能量也將被削弱。由此可知，反射光與散射光能量的強(qiáng)弱分布是由物體表面粗糙度決定的[16]，而這一特征則會在相機(jī)捕獲的圖像中表現(xiàn)出來。

根據(jù)幾何光學(xué)的反射成像定律，反射光在不同的粗糙度表面發(fā)生漫反射的擴(kuò)散程度必定不同。表面粗糙度越小，表面擴(kuò)散程度越低，反射光線集中性越強(qiáng)，這時表面成像越清晰，故當(dāng)表面成像越清晰時，圖像能量分布情況比較集中，反之能量分布越分散。而奇異值大小的分布與圖像的能量相映射[17]，則奇異值矩陣能表征圖像能量分布的情況。此外，根據(jù)香農(nóng)信息論理論，熵越大，所含的信息量越多，圖像質(zhì)量評價中也認(rèn)為熵越大，圖像就越清晰，故將熵引入奇異值矩陣中，通過構(gòu)造奇異值熵指標(biāo)來評價磨削表面粗糙度。當(dāng)奇異值熵越大時，圖像越清晰，能量分布越集中，反之越分散。

2 奇異值熵算法

四元數(shù)(Quaternions)也稱為超復(fù)數(shù)[18]，它由四個部分組成，包含一個實(shí)部和三個虛部，表達(dá)式如下：

q=a+bi+cj+dk

(2)

式中，b、c、d為實(shí)數(shù)；i、j、k為四元數(shù)的3個虛數(shù)單位；a為四元數(shù)的實(shí)部，若a=0，則稱式(2)為純四元數(shù)。

PEI等[19]發(fā)現(xiàn)了四元數(shù)的數(shù)據(jù)結(jié)構(gòu)與彩色圖像RGB顏色矢量具有良好的對應(yīng)關(guān)系，使得該技術(shù)在彩色圖像處理領(lǐng)域得到了廣泛關(guān)注。這種方法為顏色信息矢量在數(shù)學(xué)意義上提供了較為合理的數(shù)據(jù)結(jié)構(gòu)表達(dá)，對于一幅彩色圖像上任一點(diǎn)(x，y)，有

Q(x，y)=R(x，y)i+G(x，y)j+B(x，y)k

(3)

式中，Q(x，y)為彩色圖像的純四元數(shù)矩陣；R(x，y)、G(x，y)、B(x，y)分別為基于矩陣形式的紅色、綠色和藍(lán)色分量。

根據(jù)式(3)可建立彩色圖像的四元數(shù)矩陣A，本文參考文獻(xiàn)[20]給出了四元數(shù)矩陣的奇異值分解定義，其表達(dá)式如下：

(4)

Sr=diag(δ1，δ2，…，δr)

式中，Sr為圖像奇異值矩陣；δi(i=1，2，…，r)為Sr的非零奇異值，r為奇異值總數(shù)，且滿足δ1≥δ2≥…≥δr；U、V*為四元數(shù)酉矩陣。

根據(jù)式(4)可對一幅彩色圖像的四元數(shù)矩陣進(jìn)行奇異值分解，從而得到彩色圖像的奇異值矩陣，進(jìn)而可構(gòu)造出奇異值熵，計算方法如下。

對得到的圖像奇異值矩陣Sr=diag(δ1，δ2，…，δr)進(jìn)行歸一化處理：

(5)

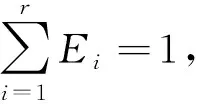
根據(jù)信息熵的定義，對四元數(shù)進(jìn)行奇異值分解，進(jìn)而構(gòu)造奇異值熵指標(biāo)(即QSE指標(biāo))，其計算表達(dá)式如下：

(6)

結(jié)合奇異值衰減迅速的特性[21]和較小奇異值可視為噪聲，本文選取奇異值數(shù)量為r=20。

3 實(shí)驗(yàn)方案設(shè)計

為更好地說明本文所提QSE指標(biāo)具備一定的優(yōu)勢和可行性，本文選取了色差(CD)指標(biāo)[9]與所提QSE指標(biāo)進(jìn)行了對比分析驗(yàn)證，且本實(shí)驗(yàn)設(shè)計方案與CD指標(biāo)的實(shí)驗(yàn)設(shè)計方案類似。圖2a為實(shí)驗(yàn)方案模型圖，其中磨削樣塊檢測面垂直于工作臺水平面，樣塊紋理方向與工作臺水平面平行，色塊(圖2b)與工作臺水平面成45°夾角。相機(jī)光軸與色塊平行，便于相機(jī)能更好地捕捉到色塊在磨削試樣表面所形成的虛像。由于LED光源具有穩(wěn)定性較好、均勻照明、亮度可控等優(yōu)點(diǎn)，因此本實(shí)驗(yàn)采用LED白色條形光源作為照射源。圖2中的主要設(shè)備包括500萬像素分辨率的彩色CCD相機(jī)、連接CCD相機(jī)的計算機(jī)、LED光源控制器和光學(xué)精密平臺。色塊的材質(zhì)為紙，尺寸為150 mm×150 mm。圖3所示為實(shí)驗(yàn)的具體流程。

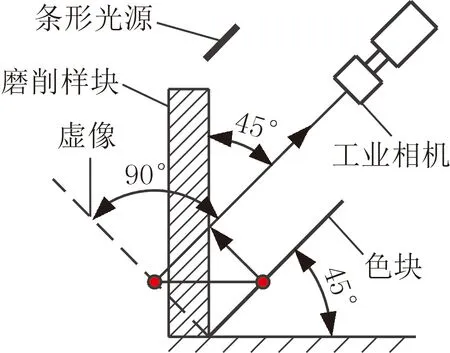
(a) 實(shí)驗(yàn)?zāi)Ｐ?(b) 色塊

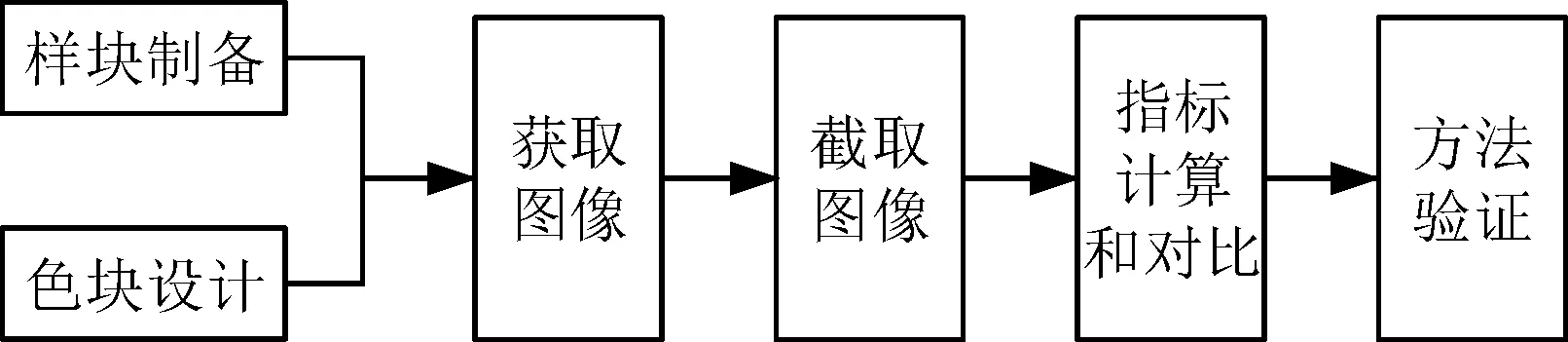
圖3 實(shí)驗(yàn)具體流程圖Fig.3 Experimental specific flowchart

4 實(shí)驗(yàn)結(jié)果與數(shù)據(jù)分析

4.1 實(shí)驗(yàn)結(jié)果

表1所示為在手動磨床上加工的20個樣塊采用觸針式測量儀得出的測量結(jié)果。表1中所有試樣的實(shí)驗(yàn)條件一致，所截取的圖像尺寸為1200 pixel×1200 pixel，并盡可能保證所截取的圖像中紅綠顏色區(qū)域?qū)ΨQ。同時，選取表1中偶數(shù)序列號的樣本作為標(biāo)定樣本，這樣使樣本分布較為均勻且粗糙度等級范圍較廣，其余10個作為驗(yàn)證樣本使用。作為對比的CD指標(biāo)的計算公式如下：

(7)

式中，R(x，y)為圖像紅色分量對應(yīng)坐標(biāo)點(diǎn)的灰度值；G(x，y)為圖像綠色分量對應(yīng)坐標(biāo)點(diǎn)灰度值。

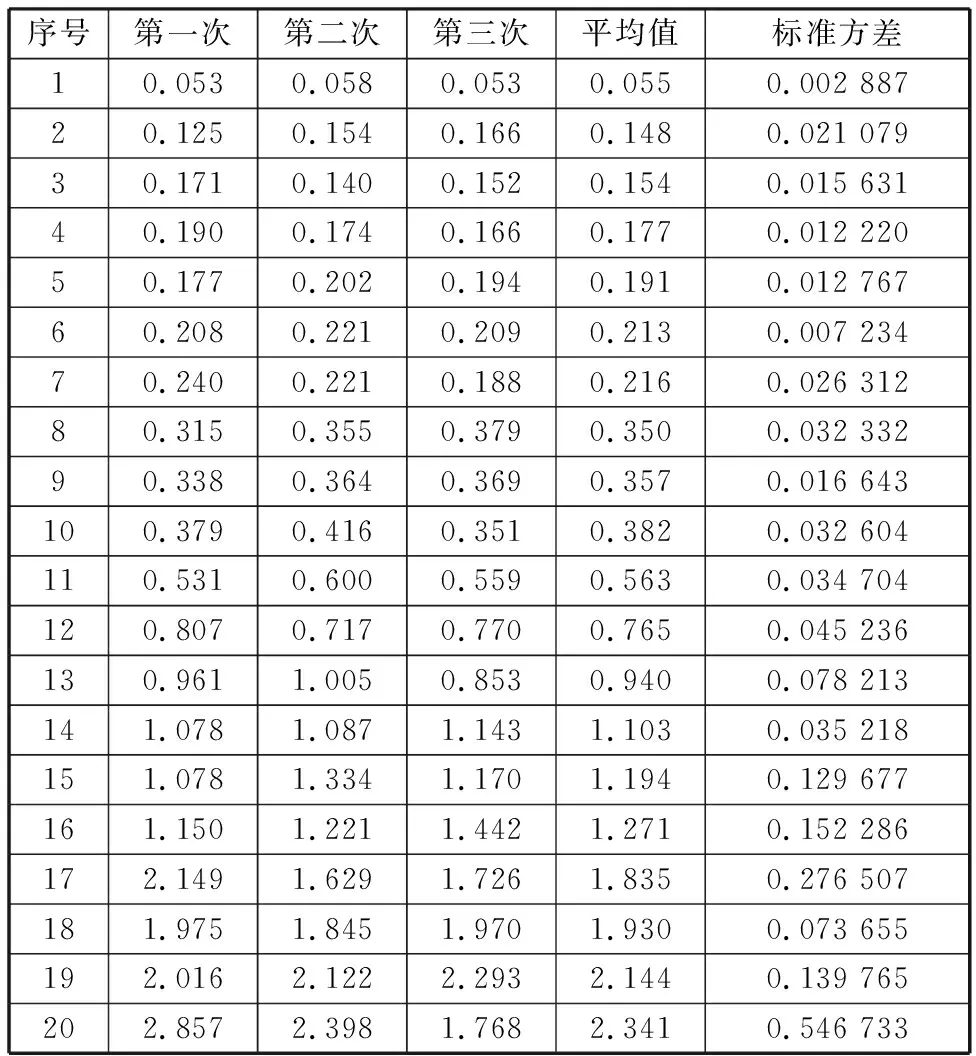
表1 觸針式測量試樣表面粗糙度

為了驗(yàn)證所提QSE指標(biāo)具備一定的預(yù)測能力，本文利用支持向量機(jī)(SVM)對樣本數(shù)據(jù)進(jìn)行回歸擬合，以達(dá)到預(yù)測表面粗糙度的目的，各指標(biāo)擬合結(jié)果如圖4所示。表2、表3所示分別為各指標(biāo)的計算結(jié)果和預(yù)測結(jié)果。為了便于指標(biāo)的對比，本文對兩種指標(biāo)值做了歸一化處理，兩種指標(biāo)歸一化之后的對比情況如圖5所示。此外，為了說明所提指標(biāo)與表面粗糙度值具有較好的相關(guān)性，本文利用皮爾遜相關(guān)系數(shù)(表4)來對指標(biāo)進(jìn)行驗(yàn)證，其計算公式如下：

(8)

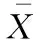
(a) CD指標(biāo)

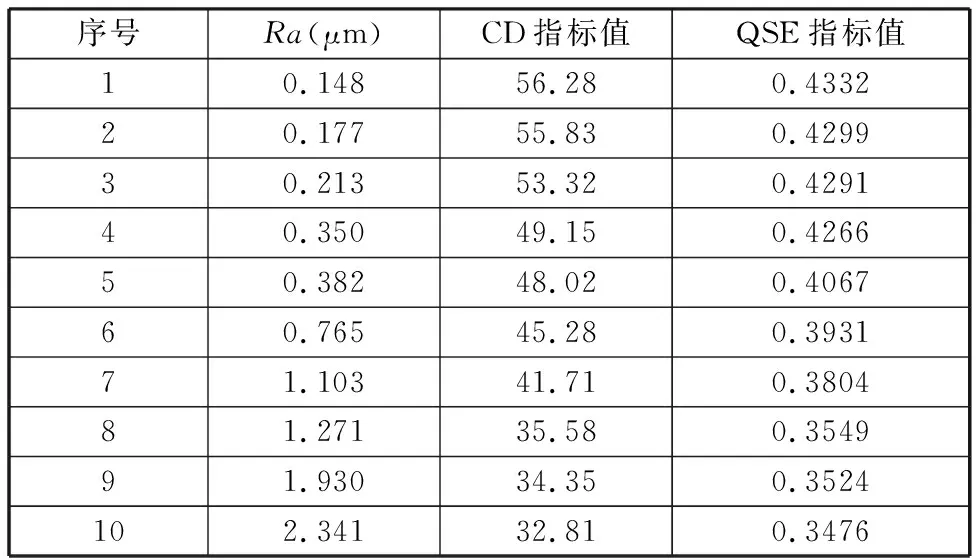
表2 不同指標(biāo)的計算結(jié)果

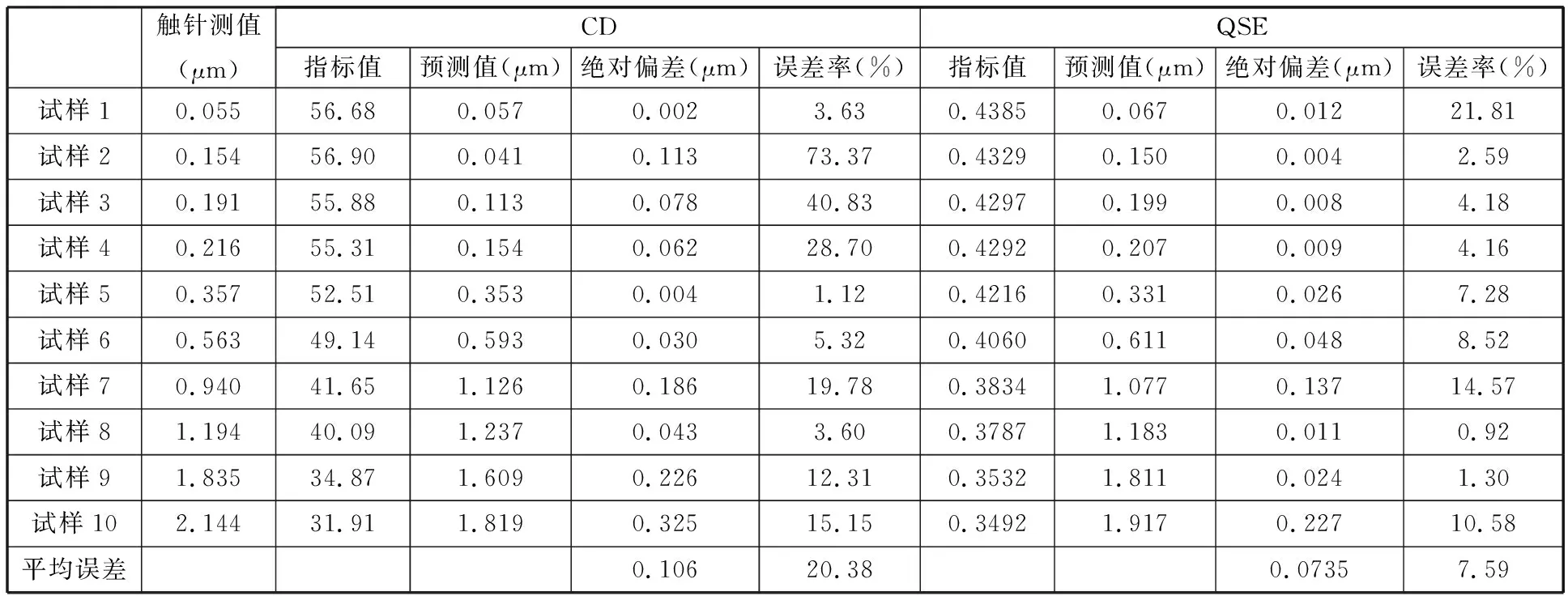
表3 驗(yàn)證樣本預(yù)測結(jié)果

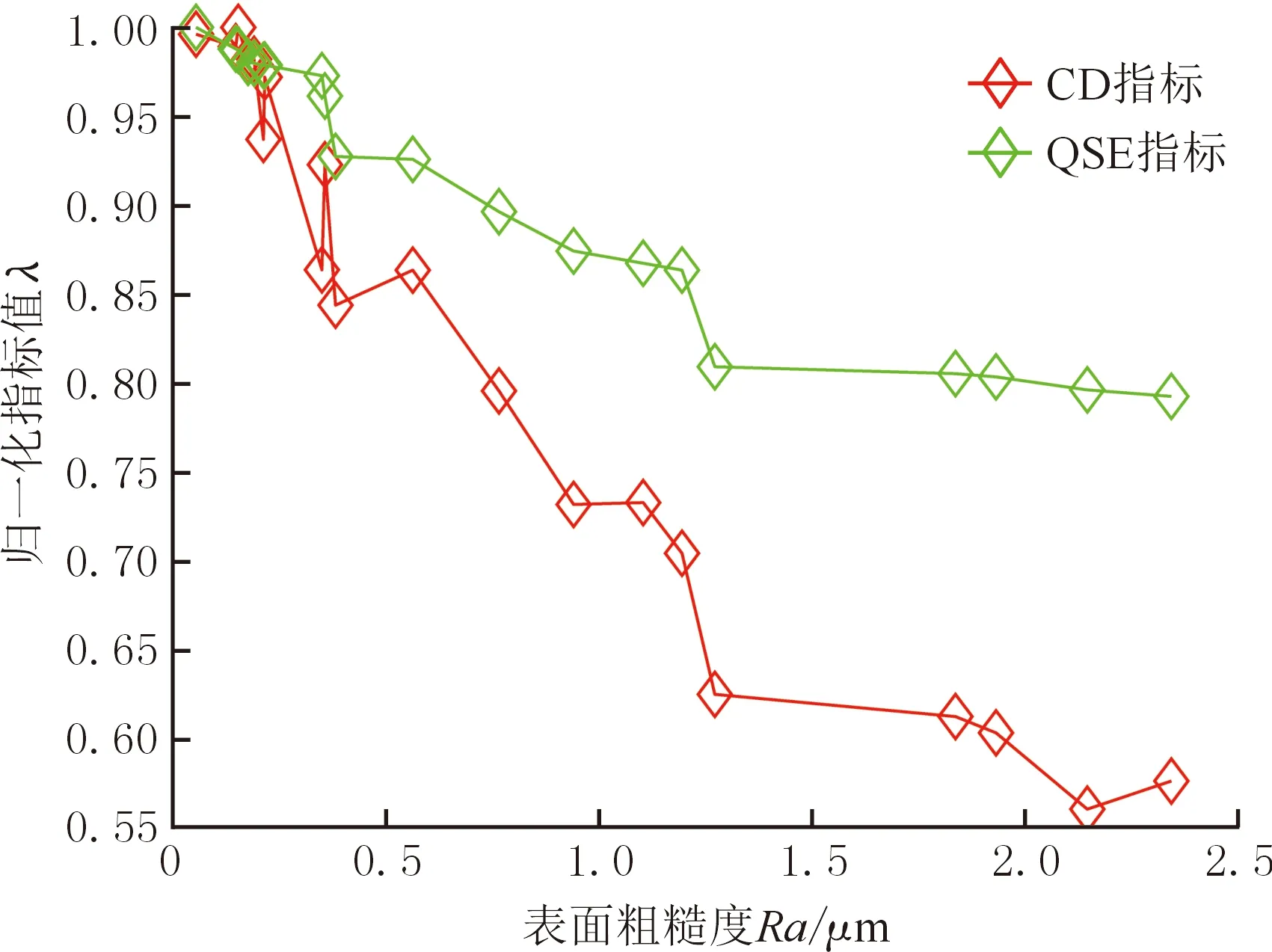
圖5 CD和QSE指標(biāo)總體趨勢對比Fig.5 Comparison of overall trends of CD and QSE indices

表4 不同指標(biāo)相關(guān)系數(shù)R值

4.2 數(shù)據(jù)分析

從表1中可以看出，利用觸針式測量設(shè)備所測得的三次測量值大多都在其平均值附近波動，且偏差程度較低，這說明每次觸針測得的表面粗糙度值較為準(zhǔn)確。為了提高測量精度，將三次測量的平均值作為磨削樣塊的表面粗糙度值。但隨著樣塊表面粗糙度的增大，其測量得到的標(biāo)準(zhǔn)方差值有逐漸增大的趨勢，產(chǎn)生這種現(xiàn)象的原因是觸針式測量儀是對試樣表面進(jìn)行線性采樣測量，其測量精確度受每次線性取樣的長度和取樣面積影響。

由表2和表3可以看出，無論是CD指標(biāo)值還是QSE指標(biāo)值都隨著表面粗糙度值的增大呈現(xiàn)單調(diào)遞減的趨勢，說明本文所提指標(biāo)具有一定的可行性。在預(yù)測能力方面，CD指標(biāo)的預(yù)測值與實(shí)際測量值的絕對偏差明顯大于QSE指標(biāo)對應(yīng)的絕對偏差；CD指標(biāo)的平均誤差率達(dá)到了20%，而QSE指標(biāo)平均誤差率僅為7%，因此QSE指標(biāo)具備更高的預(yù)測精度。兩種指標(biāo)在平均誤差率方面相差較大的主要原因是CD指標(biāo)的單調(diào)性較弱，其指標(biāo)值的波動性較大，這從圖5所示的指標(biāo)趨勢對比圖中就可以看出，而QSE指標(biāo)的檢測穩(wěn)定性較好。此外，圖5所示的CD指標(biāo)比QSE指標(biāo)表現(xiàn)出了更強(qiáng)的遞減性，產(chǎn)生這種現(xiàn)象的主要原因與兩個指標(biāo)的取值范圍有關(guān)，當(dāng)對整個圖像取CD指標(biāo)值時，其平均值受分界線附近每個像素點(diǎn)的影響較大，如圖6所示，隨著表面粗糙度值的增大，CD指標(biāo)紅綠分界線處的溝壑狀雖有所減緩，但依舊非常明顯。而QSE指標(biāo)是基于圖像的能量信息，其能量值受整幅圖像所有像素點(diǎn)變化的影響，如圖7所示，隨著表面粗糙度值的增大，QSE指標(biāo)的能量三維圖變化并不明顯，與QSE指標(biāo)相比，CD指標(biāo)變化的劇烈程度更高。

(a) Ra=0.055 μm (b) Ra=0.531 μm (c) Ra=2.341 μm圖6 CD指標(biāo)灰度三維圖Fig.6 CD index grayscale 3D image

(a) Ra=0.055 μm (b) Ra=0.531 μm (c) Ra=2.341 μm圖7 QSE指標(biāo)能量三維圖Fig.7 QSE index energy 3D image

由圖4所示的各指標(biāo)與表面粗糙度擬合情況可以看出，QSE指標(biāo)與表面粗糙度值的擬合情況優(yōu)于CD指標(biāo)，說明QSE指標(biāo)與表面粗糙度具有較好的魯棒性，表4所示的相關(guān)系數(shù)也間接證明了本文所提指標(biāo)與表面粗糙度的相關(guān)性要優(yōu)于CD指標(biāo)。如果僅比較兩種指標(biāo)的相關(guān)系數(shù)R的大小，則CD指標(biāo)的R值絕對值比QSE指標(biāo)的R值絕對值僅小0.033，但CD指標(biāo)依賴于特定的光源，而QSE指標(biāo)在無需色塊反射的情況下就可完成對試樣表面粗糙度的檢測，其適用性必定強(qiáng)于CD指標(biāo)。

此外，本文提出的奇異值熵QSE指標(biāo)較已有研究中提出的清晰度[8]和CD[9]指標(biāo)的數(shù)學(xué)解釋更為科學(xué)，可構(gòu)建數(shù)學(xué)意義上的理論模型，可為日后實(shí)現(xiàn)表面粗糙度機(jī)器視覺自動化檢測提供一定的理論依據(jù)。

5 結(jié)論

(1)本文提出了一種基于彩色圖像奇異值熵指標(biāo)(QSE指標(biāo))評價磨削表面粗糙度的方法，通過與色差(CD)指標(biāo)進(jìn)行對比實(shí)驗(yàn)分析，發(fā)現(xiàn)QSE指標(biāo)與表面粗糙度的相關(guān)性較好，且采用支持向量機(jī)擬合回歸預(yù)測的結(jié)果也較為精準(zhǔn)，表明所提指標(biāo)具備一定的可行性和優(yōu)勢。

(2)所提指標(biāo)相對評價表面粗糙度所常用的灰度圖像特征指標(biāo)而言，解決了圖像格式轉(zhuǎn)換過程中顏色信息丟失問題；對比已有的一些基于彩色圖像信息的評價指標(biāo)，該指標(biāo)將圖像顏色信息作為一個整體處理，并給出了圖像顏色信息在數(shù)學(xué)意義上具有合理解釋的矢量數(shù)據(jù)結(jié)構(gòu)表達(dá)方式及計算方法。