基于擴(kuò)展FEAST的大規(guī)模特征值求解問(wèn)題研究

李玲玲 李 華

(河南城建學(xué)院數(shù)理學(xué)院 河南 平頂山 467036)

0 引 言

非線性特征值問(wèn)題[1](Nonlinear Eigenvalue Pro-blems,NLEVP)是計(jì)算科學(xué)的熱門研究課題。其矩陣值函數(shù)的有用性，都將受到問(wèn)題求解難度的限制，伴隨著一些特有難題，例如其特征向量通常并不構(gòu)成n維向量空間的基礎(chǔ)，且矩陣值函數(shù)的特定形式會(huì)影響到求解方法的效率。然而，非線性特征值問(wèn)題與線性特征值問(wèn)題有著相同的核心難題：在n的數(shù)值較小時(shí)有效的求解方法并不一定能很好地?cái)U(kuò)展到高維問(wèn)題[2]。此類問(wèn)題通常側(cè)重于尋找少量特定的、有重要物理學(xué)意義的“特征值-特征向量”對(duì)。

大部分求解此類高維問(wèn)題的方法需要生成一個(gè)與期望特征對(duì)足夠接近的初始猜測(cè)，以確保收斂性。同時(shí)，需要使用能夠計(jì)算特征值接近的連續(xù)特征對(duì)，但不會(huì)向同一個(gè)特征對(duì)反復(fù)收斂的方法[3]。尤其在期望得到大量特征對(duì)的情況下，以上問(wèn)題更加難以解決。NLEVP算法進(jìn)一步加大了計(jì)算大量特征對(duì)的難度，導(dǎo)致不能很好地適應(yīng)在子空間內(nèi)求解的降維后的特征值問(wèn)題。而求解非線性特征值問(wèn)題所需的計(jì)算量至少與求解單個(gè)線性特征值問(wèn)題相等。因此，保持較小的維數(shù)至關(guān)重要，以確保能夠適應(yīng)較大規(guī)模的問(wèn)題。

圍道積分法是解決上述難題的一類算法[4-5]。圍道積分法利用柯西積分公式，從而僅計(jì)算其特征值位于復(fù)平面的用戶定義特定區(qū)域中的特征對(duì)。這樣就不需要計(jì)算初始猜測(cè)，并對(duì)維數(shù)為n的原始問(wèn)題中距離很近的特征值進(jìn)行了分離。此外，圍道積分法支持大量特征對(duì)的高效并行計(jì)算，通過(guò)將復(fù)平面中的感興趣區(qū)域分割為不相交的子區(qū)域，在每個(gè)子區(qū)域中獨(dú)立求解特征值，且與其他子區(qū)域的特征值無(wú)關(guān)。

而線性FEAST算法[6-7]是求解線性特征值問(wèn)題的圍道積分法樣例。該算法能夠求解大規(guī)模廣義線性特征值問(wèn)題，具有較好的魯棒性和優(yōu)秀的并行可擴(kuò)展性。本文對(duì)線性FEAST算法進(jìn)行推廣，使其能夠求解非線性特征值問(wèn)題，并通過(guò)求解一些物理模型問(wèn)題來(lái)解釋該算法的特性。

1 非線性特征值問(wèn)題

給定一個(gè)非空的開集D?C和一個(gè)矩陣值函數(shù)T:D→Cn×n，考慮一個(gè)非線性特征值問(wèn)題：找到標(biāo)量λ∈D和非零向量x∈Cn、y∈Cn，使得：

T(λ)x=0 且y·T(λ)=0

(1)

本文將(λ,x,y)稱為T的特征三元組，(λ,x)或(λ,y)均被稱為特征對(duì)。對(duì)于T(λ)=λI-A和T(λ)=λB-A，通過(guò)式(1)分別將其簡(jiǎn)化為標(biāo)準(zhǔn)特征值問(wèn)題Ax=λx和廣義特征值問(wèn)題Ax=λBx。廣義非線性特征值問(wèn)題的特性與線性特征值問(wèn)題有著很大的不同，例如T(即使是正則值，即det(T(λ))≠0)可能有無(wú)窮多個(gè)特征值，屬于不同特征值的特征向量不一定是線性無(wú)關(guān)的，且一個(gè)孤立特征值的代數(shù)重?cái)?shù)雖然是有限的，但不受問(wèn)題大小n的限制[8]。所有這些特性，使得廣義非線性特征值問(wèn)題非常難以求解。關(guān)于該問(wèn)題更詳細(xì)的描述，可參考二次特征值問(wèn)題的相關(guān)文獻(xiàn)或廣義非線性特征值問(wèn)題[9]。

為便于討論，本文側(cè)重于研究方陣類多項(xiàng)式特征值問(wèn)題。找到標(biāo)量λ∈D?C和非零向量x,y∈Cn，以使得：

P(λ)x=0y·P(λ)=0

(2)

式中：P(λ)為n×n的矩陣多項(xiàng)式。

(3)

若P為正則，即det(P)≠0，則式(2)有r個(gè)有限特征值(det(P)=0的根)和kn-r個(gè)無(wú)限特征值(復(fù)特征值)。通過(guò)線性化，可知k次的n×n矩陣多項(xiàng)式P(λ)有著kn個(gè)特征值(有限或無(wú)限)，最多kn個(gè)右相關(guān)特征向量，及最多kn個(gè)左相關(guān)特征向量。

2 擴(kuò)展FEAST算法

2.1 FEAST算法

原始FEAST算法被用于求解廣義特征值問(wèn)題，即T(λ)=λB-A，其是一個(gè)子空間迭代方法，使用Rayleigh-Ritz投影和近似光譜投影器作為濾波器。FEAST計(jì)算與位于復(fù)平面中用戶定義的特定區(qū)域中的特征值相對(duì)應(yīng)的特征對(duì)。因此，該算法可被用于并行計(jì)算大量特征對(duì)，其中將復(fù)平面分割為不相交的區(qū)域集合，并獨(dú)立求解每個(gè)區(qū)域中的特征對(duì)(與其他區(qū)域中的特征對(duì)無(wú)關(guān))。

FEAST首先將任意隨機(jī)初始子空間X(0)投影到感興趣特征向量所覆蓋的子空間來(lái)選擇感興趣的特征向量和特征值，然后使用Rayleigh-Ritz程序[10]在該子空間中提取特征值/特征向量的近似。通過(guò)使用復(fù)圍道積分來(lái)完成向感興趣子空間的投影：

(4)

式中：Q為新的投影子空間，在包圍著感興趣特征值的圍道中完成積分。若精確完成積分，則濾波器ρ(A,B)成為光譜投影器，ρ(A,B)=XYHB，其中X和Y分別是與感興趣特征值(即位于閉合曲線內(nèi)的特征值)相關(guān)的精確的右特征向量矩陣和左特征向量矩陣。然而在實(shí)踐中，無(wú)法在式(4)中精確完成積分，因此使用求積規(guī)則對(duì)其進(jìn)行逼近。則FEAST算法實(shí)際生成的子空間為：

(5)

式中：zj和wj分別為積分節(jié)點(diǎn)和權(quán)值，通過(guò)求解線性系統(tǒng)(zjB-A)Qj=BX(0)來(lái)完成求和。由于每個(gè)線性系統(tǒng)均獨(dú)立于其他系統(tǒng)，因此可以并行地同時(shí)求解。FEAST通過(guò)反復(fù)應(yīng)用求和，將得到的子空間Q正交化，并將其用于Rayleigh-Ritz程序中，對(duì)感興趣特征向量的估計(jì)進(jìn)行迭代式改進(jìn)。

本文旨在利用FEAST框架的優(yōu)點(diǎn)來(lái)求解NLEVP,使用圍道積分對(duì)固定維數(shù)的子空間進(jìn)行迭代優(yōu)化，以求解特征值位于復(fù)平面的用戶定義區(qū)域中的特征對(duì)。

2.2 NLFEAST算法

線性FEAST算法可以解釋為在復(fù)平面上使用多個(gè)移位的平移-逆迭代的推廣。利用相似的推理，假定非線性FEAST(NLFEAST)算法是使用多個(gè)移位的非線性移位-逆迭代的推廣：

x(i+1)=T(z)-1T′(λ(i))x(i)

(6)

式中：x(i)和λ(i)為特征向量和特征值在迭代i處的估計(jì);T′(·)為T(·)的導(dǎo)數(shù);z為復(fù)平面中位于感興趣特征值附近的移位。由此預(yù)期非線性FEAST圍道積分(單個(gè)向量)將類似于：

(7)

積分圍道包圍著感興趣特征值。但在實(shí)踐中，式(7)中的更新程序未能向正確的特征值-特征向量對(duì)收斂。這是因?yàn)樵谑?7)中使用恒定移位z會(huì)造成非線性逆迭代向錯(cuò)誤的解收斂。

原始FEAST算法可以解釋為移位-逆迭代的推廣，使用圍道積分以高效地同時(shí)使用多個(gè)移位。而非線性FEAST算法則可以解釋為殘差逆迭代的推廣，使用圍道積分以高效地同時(shí)使用多個(gè)移位。本文給出了非線性FEAST算法的算法框架，如算法1所示。

算法1T(λ)x=0時(shí)的NLFEAST算法

步驟1設(shè)子空間Q=X(0)，對(duì)Q的列向量進(jìn)行正交歸一化。

步驟2求解投影后的非線性特征值問(wèn)題:

QHT(λ)Qy=0

(8)

以得到近似特征對(duì)(λ,Qy)。

Λ=diag(λ1,λ2,…,λm0)X=[Qy1,Qy2,…,Qym0]

(9)

步驟5通過(guò)執(zhí)行數(shù)值積分對(duì)搜索子空間進(jìn)行更新：

(10)

使用求積規(guī)則并求解線性系統(tǒng)：

(11)

步驟6對(duì)新的搜索子空間Q的列向量進(jìn)行正交歸一化(例如使用QR分解)，并回到步驟2。

非線性FEAST算法中Rayleigh-Ritz步驟與線性算法中的工作原理相同：將殘差函數(shù)T(λ)投影到子空間Q上，然后選擇合適的方法(本文使用了簡(jiǎn)單線性化)對(duì)維數(shù)降低后的非線性特征值問(wèn)題進(jìn)行求解。得到的Ritz值及Ritz向量被用作期望特征對(duì)的新估計(jì)。

用于Rayleigh-Ritz程序的子空間，即通過(guò)執(zhí)行圍道積分所生成的子空間，應(yīng)該是正交歸一化的(如使用QR分解)。正交歸一化能夠防止期望特征向量的范數(shù)出現(xiàn)發(fā)散，并防止Rayleigh-Ritz程序生成偽特征對(duì)(即與全尺寸特征值問(wèn)題的任意特征對(duì)均不對(duì)應(yīng)的Ritz對(duì))，由此提升了FEAST迭代的數(shù)值穩(wěn)定性。

在m0=1和nc=1的情況下，算法1大致等價(jià)于殘差逆迭代。這兩種算法的區(qū)別在于非線性特征值和特征向量的估計(jì)方式不同，以及步驟5中更新向量的縮放差別。算法1通過(guò)求解步驟2中的投影非線性特征值問(wèn)題來(lái)計(jì)算近似特征向量和近似特征值，而殘差逆迭代則使用步驟5中的子空間更新程序?qū)铺卣飨蛄窟M(jìn)行更新。

3 數(shù)值分析實(shí)驗(yàn)

將本文的NLFEAST算法在3個(gè)有實(shí)踐意義的多項(xiàng)式特征值問(wèn)題上做數(shù)值分析實(shí)驗(yàn)。

3.1 樣例1：非過(guò)阻尼質(zhì)點(diǎn)彈簧系統(tǒng)

考慮一個(gè)與質(zhì)點(diǎn)彈簧系統(tǒng)[11]相關(guān)的自共軛(Hermitian)二次特征值問(wèn)題：

T(λ)x=(λ2A2+λA1+A0)x=0

(12)

式中:

參照文獻(xiàn)[12]，首先分析非過(guò)阻尼系統(tǒng)。本文設(shè)n=1 000，并選擇τ=0.620 2，k=0.480 7。圖1展示了Q的所有特征值。要考慮計(jì)算的特征向量的特征值沒有虛部；質(zhì)點(diǎn)彈簧系統(tǒng)原運(yùn)動(dòng)公式的解的指數(shù)增長(zhǎng)或衰減是這些特征向量的線性組合。

圖1 非過(guò)阻尼質(zhì)點(diǎn)彈簧系統(tǒng)的所有特征值

使用算法1中的非線性FEAST方法，計(jì)算這20個(gè)實(shí)特征值的近似。選擇的圍道為一個(gè)橢圓，其中心為區(qū)間(-1.6,-1.5)的中點(diǎn)，使用nc=16個(gè)求積節(jié)點(diǎn)，實(shí)軸方向的半徑ra=0.05，虛軸方向的半徑rb=0.003 5，殘值的收斂標(biāo)準(zhǔn)為tol=10-10。在維數(shù)m0=22的子空間中，非線性FEAST算法在三次迭代中找到了區(qū)間內(nèi)的全部m=20個(gè)特征值。表1給出了使用線性化方法和非線性FEAST算法得到的特征值近似。為完備性起見，本文還列舉了所有的最終殘值，即‖ri‖2=‖T(λi)xi‖2。

表1 非過(guò)阻尼質(zhì)點(diǎn)彈簧系統(tǒng)在的所有實(shí)特征值列表

續(xù)表1

表2給出了當(dāng)搜索區(qū)間(a,b)增大時(shí)，收斂所需的非線性FEAST迭代次數(shù)。當(dāng)求積節(jié)點(diǎn)nc的數(shù)量保持在16個(gè)不變時(shí)，擴(kuò)大搜索區(qū)間的影響等同于將求積節(jié)點(diǎn)放置在遠(yuǎn)離感興趣特征值的地方，由此使得圍道積分的準(zhǔn)確度降低。區(qū)間大小的適度變化僅會(huì)造成收斂所需的工作量稍微上升；而區(qū)間大小的較大變化往往會(huì)要求非線性FEAST迭代次數(shù)隨之按比例增加。實(shí)踐中，與期望特征值分布相關(guān)的搜索區(qū)間的大小而造成的性能降低，可以通過(guò)簡(jiǎn)單地使用大量求積節(jié)點(diǎn)而緩解，這種情況下需要更多的并行處理能力來(lái)同時(shí)求解更多的線性系統(tǒng)。

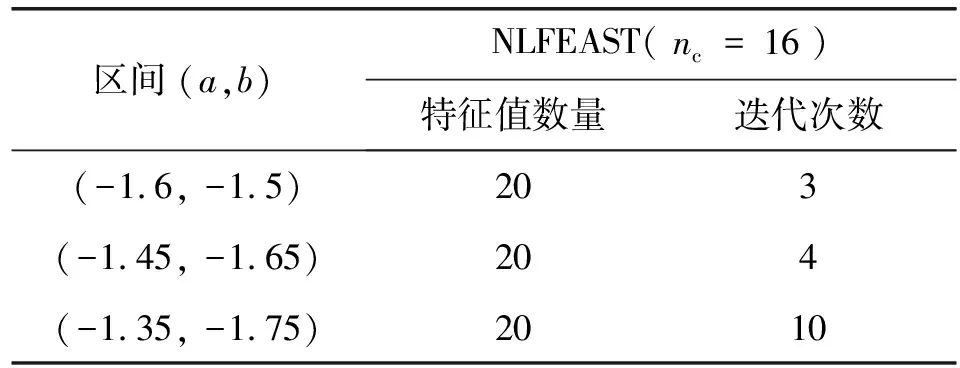
表2 非過(guò)阻尼質(zhì)點(diǎn)彈簧系統(tǒng)的特征值數(shù)量

3.2 樣例2：一維散射共振

非線性特征值問(wèn)題的另一個(gè)應(yīng)用是開邊界量子透射問(wèn)題。在開邊界量子投射問(wèn)題中，需要計(jì)算量子勢(shì)的準(zhǔn)束縛態(tài)，其中粒子可以進(jìn)入或離開系統(tǒng)，最好不要對(duì)外部源進(jìn)行顯式建模。這可以通過(guò)求解非線性特征值問(wèn)題來(lái)實(shí)現(xiàn)?？紤]一個(gè)開邊界量子透射問(wèn)題的樣例，即一維散射共振問(wèn)題，其中包含以下緊支有限二乘模型：

(13)

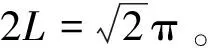
在n=302個(gè)點(diǎn)的網(wǎng)格上的有限元離散化得到大小為302的帶散射共振的二次特征值，其特征值結(jié)果如圖2所示?？梢钥闯?，r=15.5為半徑的圓內(nèi)共計(jì)22個(gè)復(fù)散射共振。非線性FEAST使用nc=16個(gè)求積節(jié)點(diǎn)，求解子空間維數(shù)m0=30、V0=10的散射共振問(wèn)題。4次迭代計(jì)算這22個(gè)散射共振的近似值(收斂容差10-10)，其結(jié)果如圖3所示。

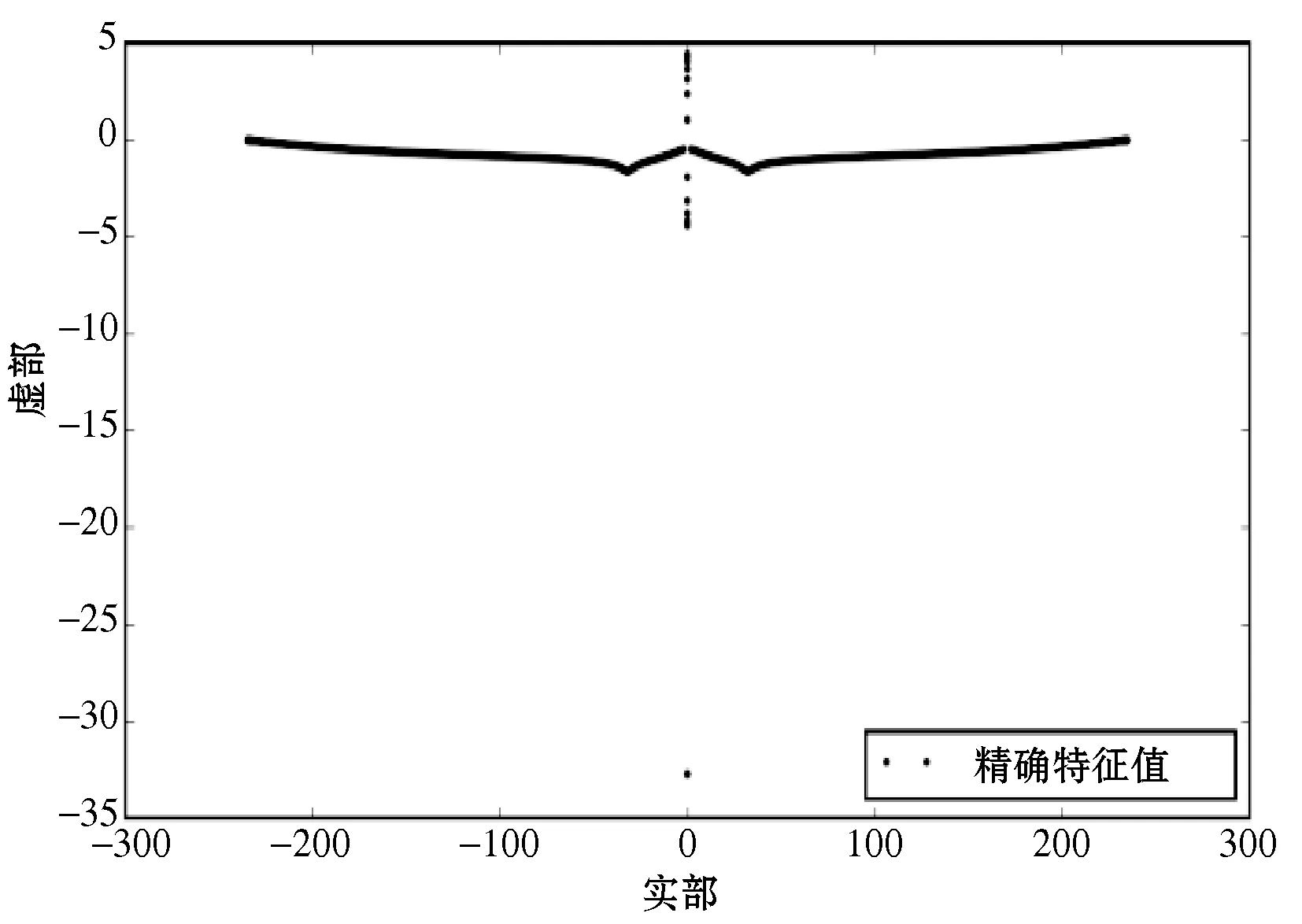
圖2 散射共振的所有特征值

圖3 一維散射共振的NLFEAST算法特征值估計(jì)

3.3 樣例3：軌道振動(dòng)

較長(zhǎng)軌道的振動(dòng)可建模為以下形式的二次特征值問(wèn)題[13]：

T(λ)=λ2I+λ(I+A2)+A2+A+I

(14)

式中：A為一個(gè)n×n的轉(zhuǎn)換矩陣。對(duì)于任意維數(shù)n，通過(guò)求解以下二次方程給出式(14)的二次特征值問(wèn)題的特征值：

(15)

式中：μk=-4sin2((k-1)π/n)(1≤k≤n)為矩陣A的特征值，特征值以復(fù)共軛對(duì)的形式出現(xiàn)。

考慮A的維數(shù)為n=50 000，使用NLFEAST算法計(jì)算與區(qū)間[-7.119 2,-6.965 0]內(nèi)的特征值相對(duì)應(yīng)的250個(gè)特征向量，其中圓形圍道的圓心坐標(biāo)為(-7.042，0)，半徑0.077 1。圖4展示了其特征值位置和積分圍道。

圖4 軌道振動(dòng)特征圖示

為進(jìn)一步比較，本文還使用Beyn法利用相同的積分圍道計(jì)算相同的250個(gè)特征值。表3給出了Beyn法在使用不同的子空間維數(shù)和各種數(shù)量的求積節(jié)點(diǎn)時(shí)，與積分圍道內(nèi)的特征值相對(duì)應(yīng)的特征向量的最終特征向量殘值。與NLFEAST算法一樣，僅考慮殘值低于10-2的特征向量為正確特征向量，由此排除偽特征值。

表3 使用Beyn法計(jì)算特征值時(shí)的向量殘值

表3的結(jié)果表明，Beyn法和NLFEAST算法在計(jì)算一個(gè)解時(shí)需要的計(jì)算量大致相當(dāng)。例如，當(dāng)m0=500，nc=8時(shí)，NLFEAST算法需要6次迭代以收斂至約10-11，即總計(jì)500×8×6=24 000個(gè)線性系統(tǒng)解;Beyn法在m0=500時(shí)需要nc=64個(gè)求積節(jié)點(diǎn)以收斂至殘差10-12的特征向量，即對(duì)應(yīng)于500×8×8=28 500個(gè)線性系統(tǒng)解。

以上兩種方法的差異源于計(jì)算方式的不同。Beyn法理論上可以并行求解所有相關(guān)的線性系統(tǒng)，而NLFEAST算法則可以并行求解最多m0×nc個(gè)線性系統(tǒng)。Beyn法的并行性較高，但需要計(jì)算更多數(shù)量的矩陣分解。在上述案例中，Beyn法需要64次矩陣分解，而NLFEAST算法僅需8次。

4 結(jié) 語(yǔ)

本文提出了線性FEAST特征值算法的一個(gè)擴(kuò)展算法，以求解非線性特征值問(wèn)題。提出的NLFEAST算法使用與線性FEAST算法相同的一系列運(yùn)算，但修改了圍道積分，支持在求解非線性特征值問(wèn)題時(shí)使用固定移位集合和固定子空間維數(shù)。線性FEAST算法可被解釋為移位和逆迭代的使用多次移位的推廣，而NLFEAST算法則可被解釋為殘差逆迭代的使用多次移位的推廣。本文改進(jìn)數(shù)值圍道積分提升了近似特征向量子空間的維數(shù)，從而系統(tǒng)地提高了算法的收斂速度。