基于改進灰狼優化的復雜網絡重要節點識別算法

顧秋陽，吳寶，孫兆洋，池仁勇

（1.浙江工業大學管理學院，浙江 杭州 310023；2.浙江工業大學中國中小企業研究院，浙江 杭州 310023；3.中國標準化研究院高新技術標準化研究所，北京 100191）

1 引言

隨著近年來信息技術的迅速發展，復雜網絡節點間的交流、互動形式日趨多樣化，由此產生海量的復雜網絡數據，其中存在大量節點間的信息交互集。對上述數據進行挖掘，尋找具有影響力的節點，并基于此有效阻止負面信息傳播、宣傳正面信息、提升推薦效率已成為學術界關注的焦點之一。據中國互聯網絡信息中心（CNNIC）發布的第47 次《中國互聯網發展狀況統計報告》，截至2020 年12 月，我國網民規模達9.89 億，互聯網普及率達70.4%，較2020 年3 月增長5.9%；同期，我國網絡新聞用戶達7.42 億，占網民整體的75.1%，社交應用使用率高達網民總量的85.5%。2019 年，國家互聯網信息辦公室發布的《數據安全管理辦法》中，對社交網絡平臺提出了新的要求。網絡運營者應采取措施督促提醒用戶對自己的網絡行為負責、加強自律，對于節點通過網絡轉發給其他節點制作的信息，應自動標注信息制作者在該社交網絡上的賬戶或節點標識。這往往會選擇合適的節點群體進行信息傳播，而社交網絡龐大的節點群體會使病毒式傳播成為在線社交網絡中的最大受益者[1-4]。由于進行節點選取和控制的成本有限，因此只能在復雜網絡中選擇一組有限數量的種子節點，使其在復雜網絡中傳播信息，最終實現影響力最大化問題[5]。本文需解決的問題為如何有效識別最具影響力的節點，并將其加入種子節點集中，該問題又被稱為節點影響力最大化（IM,influence maximization）問題[6-8]。盡管如文獻[9-10]所示，在現有的節點影響力最大化算法中，節點的行為和興趣已被視為信息傳播過程的重要因素，但此類信息并非從真實復雜網絡中獲得的，故只有網絡結構信息可用于識別影響力較大的節點。

目前，已有學者提出多種用于復雜網絡重要節點識別的擴散模型[11-13]，可用于模擬信息擴散過程建模及種子節點影響力。由于節點影響力最大化問題的搜索范圍往往很大，故評估所有可能的節點子集以定位最佳種子節點集為NP-hard 問題[14]。而真實復雜網絡的輻射范圍很廣，故利用影響力最大化模型來衡量節點影響力往往較費時。常用于識別影響力最大的節點集的方法是選擇中心節點，可采用多種方法來度量復雜網絡結構的中心度，如網絡度[15]、介數中間性[16]、緊密度[17]、k-shell[18]及改進k-shell[19]。但通過測量網絡結構的中心度對影響力最大化節點進行識別通常不是解決此問題的最好方法。另外，有研究認為節點影響力最大化問題屬于優化問題，并采用貪婪算法、啟發式算法及元啟發式算法等來解決該問題。Wang 等[20]提出了改進貪婪算法，以此求得擴散模型的最優解，盡管該算法的精度較高，但其計算過程十分復雜，故在大規模復雜網絡中并不實用[21]。而Bao 等[22]針對影響力最大化問題提出的啟發式算法的時間復雜度和精度較低，但啟發式算法得到的值在可達局部中最優[23]。

為識別一組接近最優的具有最大影響力的節點，首先需要對節點影響力進行度量，然后找到最有影響力的節點集。本文首先使用基于Shannon 熵的指標來衡量節點影響力，并將該問題轉化為優化問題，采用一種改進灰狼優化算法解決該問題[24]，并利用真實復雜網絡數據集進行數值計算。

2 相關工作

本文基于圖論對復雜網絡圖進行建模，其中，節點代表復雜網絡節點，邊代表節點間存在的關系。首先對一些經典的擴散模型以及用于影響力最大化問題的常見方法進行回顧。擴展模型常用于模擬真實世界中的傳播過程，常用的擴散模型包括閾值模型[25]、級聯模型[26]和傳染病模型[27]。其中，獨立級聯模型（IC,independent cascading）為現今應用最廣泛的擴散模型之一[26]，其中每個節點都處于活躍或非活躍模式中。為度量種子節點集S的影響力，將最初放置在種子節點集S中的節點定義為活躍節點，并將所有其他節點定義為非活躍節點。在每個時間段t中，時間段t?1 中被激活的每個節點都有一次機會激活其非活躍的鄰節點（激活概率為p），該過程會一直持續到該時間段內沒有新節點為止。最后，在此過程迭代多次后得到的激活節點數量即為節點集S的影響范圍。

有關節點影響力最大化問題，現有研究可分為兩大類。第一類為識別節點影響力并對其進行排序。在多數相關研究中，根據網絡結構和節點網絡位置，可使用中心性度量法來衡量節點影響力。雖然中心性方法計算較簡單，也能較好地確定節點活躍度[28]，但這類方法在識別Top-k 影響力節點時精度不高。Bao 等[22]提出了一種優化種子節點集的方法，使其總體影響范圍最大化，并在考慮節點影響力的同時，考慮了網絡中的節點距離，以進一步提高重要節點識別算法的有效性。第二類節點影響力最大化方法在考慮網絡可達性的基礎上，將該問題轉化為優化問題（如貪婪算法、啟發式算法、元啟發式算法等）。關于貪婪算法，Kempe 等[25]對含有k個最具影響力的種子節點集S進行識別，并迭代k次，每次迭代時使用擴散模型來估計該集合的影響力。

為改善節點影響力最大化問題優化過程中存在的時間復雜度問題，研究者提出了一系列啟發式算法，用于選擇節點影響力最大化集合。啟發式算法通過使用遞歸法給每個節點分配一個分數，并選擇分數最高的top-k 節點作為種子節點集。Chen 等[29]提出了2 種方法用于選擇種子節點集，首先以每個節點度作為影響力指標，并以k次迭代選擇種子節點集。在每個步驟中，都可將影響力最大的節點添加到種子節點集中。如節點v加入種子節點集，則其鄰節點影響力將會隨之降低，且被選為種子節點的概率也會降低。Wang 等[30]所提度懲罰法嘗試同樣方法來選擇種子節點集，將節點v選為種子節點，就需懲罰二跳內的所有鄰節點，并降低被選為種子節點的概率。該方法可有效減少網絡中種子節點的重疊現象，并增加節點分散性。Guo 等[31]提出了基于距離圖對具有適當距離的節點進行識別和分類，以使各組中的節點對間距離都大于閾值。Bao 等[22]提出了啟發式聚類算法，確定每對節點間的相似度，并選擇各集群中影響力最大的節點作為種子節點，將節點影響最大化問題建模為多目標優化問題。

元啟發式算法通常首先定義適應度函數，將節點影響力最大化問題建模為優化問題，并應用各種改進優化算法對該問題進行解決。Jiang 等[32]將種子節點集S的影響定義為預期擴散值（EDV,expected diffusion value）。Gong 等[21]引入改進EDV值，并使用粒子群優化（PSO,particle swarm optimization）算法來優化目標函數。Sun[33]用復制對稱平均場理論來解決節點影響力最大化問題。本文首先定義了適應度函數，然后利用灰狼優化算法提出了一種適應度函數對重要節點識別方法進行優化。

3 算法設計

3.1 預備知識

本文首先利用熵的概念定義了適應度函數，并將節點影響力最大化問題設計為優化問題，隨后利用改進灰狼優化算法解決該問題。根據Shannon 熵值，如X∈{x1,x2,…,xn}，且pi為目標xi被選擇的概率，其中，可根據式(1)計算X的熵。

灰狼優化（GWO,gray wolf optimization）算法[24]是一種基于種群的演化算法，其靈感來源于灰狼的狩獵行為。如圖1 所示，灰狼遵循嚴格的社會等級制度，在社會中主要分為α、β、γ、δ這4 種。α狼、β狼及γ狼在狩獵過程中主要負責攻擊，而δ狼在團隊中扮演替罪羊的角色。根據不同狼的特征，可將GWO 算法建模如下。首先，隨機生成一組解，使得每個解都與一頭狼相對應，以表示其位置。其中，適應性排名第一的為α狼，適應性排名第二和第三的分別為β狼和γ狼，剩余則為δ狼。該算法根據α、β、γ狼的位置進行空間搜索，以找到獵物的位置（即最優解）。上述3 種狼可以預測獵物位置，而δ狼則根據另外3 種狼的位置來改變自身位置，從而找到離獵物更近的位置，該算法嘗試在迭代過程中找到最優解。在每次迭代過程中，δ狼都會試圖根據其他狼群的位置來改變自身位置。在每次迭代t中，δ狼都會根據迭代次數t+1確定自身的新位置，即Xi(t+1)，具體如式(2)所示。

其中，每只δ狼都會試圖根據Y1、Y2、Y3來確定更優位置，Y∈[Y1,Y2,Y3]值可根據狼的當前位置和α狼的位置計算得到，具體如式(3)所示。

其中，Dα的計算式為

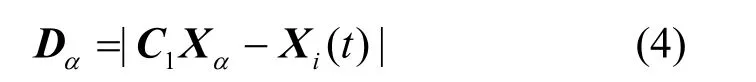
其中，t表示當前迭代次數，Xi(t)表示本次迭代中狼i的位置，而Xα表示α狼的位置。結合β狼和γ狼的當前位置，利用式(5)可計算得到Y2和Y3的值。

其中，Dβ和Dγ的值可由式(6)計算得到。

其中，Xβ和Xγ分別表示β狼和γ狼的位置，A和C分別表示如式(7)所示的系數向量。

其中，r1和r2表示區間[0,1]內的隨機值，a值為迭代過程中從2 線性趨近于0 的控制參數。a值在時段t中的計算方法如式(8)所示。

其中，maxt表示重要節點識別算法的迭代次數。在迭代過程中，狼群間的位置矛盾減少，算法逐漸收斂，最后得到α狼最優解，并將其作為最優解決方案。經典灰狼優化算法的執行過程如算法1 所示[25]，其中n表示種群規模。

算法1灰狼優化算法

輸入狼α,β,,γ δ的位置

輸出集合{xα,xβ,xγ,xδ}

本文使用無向圖G=(V,E)對復雜網絡圖進行建模，其中，V={v1,v2,…,v|V|}表示復雜網絡節點集，E表示節點間的關系邊集。邊ei,j∈E表示2 個節點vi和vj間的距離，且這2 個節點為鄰節點。N i?V表示節點vi的鄰居，di=|Ni|表示節點vi的影響力。表示節點vi的二跳鄰節點（即鄰節點的鄰節點）。節點影響力最大化問題的目標是識別具有k個節點的集合S，以啟動傳播過程，從而使傳播影響最大化，即激活節點數量最大化。在本文的其余部分中，S′表示種子節點集S中節點的鄰節點或二跳鄰節點的節點集合。

3.2 適應度函數

本文選擇節點作為種子節點集中的節點，其中每個節點都具有較高影響力，且選擇的集合盡可能地覆蓋整個網絡，以保證信息傳播最大化。在傳播過程中，節點vj S′∈ 被激活，即接受信息，可使用式(9)進行計算。

其中，pi,j表示信息從vi傳播到vj的概率。式(9)可用來計算節點vj收到其鄰節點發送信息的概率，且其鄰節點都為S集成員。如果節點vj在S集中沒有鄰節點，則可將其視為零集合。而式(9)等號右邊第二項可用來計算節點vj收到其二跳鄰節點發送信息的概率，且其二跳鄰節點也為S集中的成員。這兩部分都根據概率規則進行求和，在傳播過程中不同節點不會產生相同影響。如果影響力較大的節點接收到該信息，則其可能會傳播至復雜網絡的其他領域，各節點v j∈S′值。本文所提基于改進灰狼優化的重要節點識別算法中，適應度函數為。使用本文所提IGW-CNI算法尋找種子節點，以使S′集中的節點數量最大化，且其中所有節點都具有較大影響力。在運用求和運算符后，將S′集中有限的具有較高價值的節點和無價值節點相組合，使適應度函數計算得到的值實現最大化。在此情況下，如果無法將信息傳播給有影響力的節點，會導致所選節點的影響力大幅降低。在適應度函數中使用熵來解決此問題，使節點在S′集中的均衡節點能更有效提升集S的影響力。另一方面，熵值隨著S值的增大而增大，故需進行歸一化。集S的適應度熵值可定義為

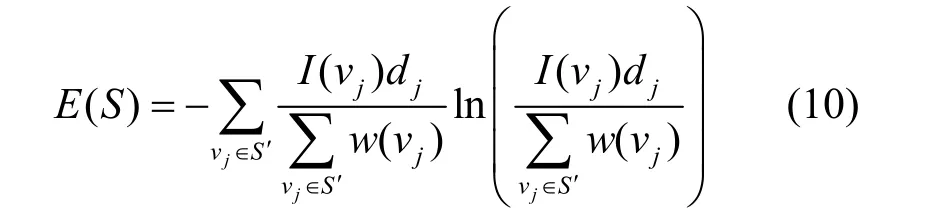
3.3 改進灰狼優化算法

參考文獻[34]的結論可知，度為1 的節點被選為種子節點的概率非常低。在許多真實復雜網絡中，大部分節點只存在一個鄰節點。為有效降低本文所提IGW-CNI 算法的時間復雜度，僅將影響力大于1 的節點選為候選種子節點，并將這些節點表示為。而每只狼（即每個解）都存在2 個屬性，即位置和對應的種子節點集。狼i的位置可表示為帶有節點|V′| 的向量xi，其中第j個節點表示節點被選為種子節點的概率。狼i對應的種子集為Si，其中包含k個節點，且其值在Xi中最高。

算法2 給出了本文所提IGW-CNI 算法的具體流程。首先，隨機生成n個主要解，并利用隨機位置函數生成每個隨機解；其次，利用式(10)來計算解的適應度值，并根據解的適應度值來選擇確定α、β、γ狼。進行maxt次迭代操作，以最大化適應度。在每次迭代過程中，更新δ的位置，并給出更新后的位置。為每只狼i確定種子集Si，而后計算每個子集Si的適應度值，并根據適應度值，將最佳解更新α、β、γ狼；隨機更新β、γ狼的位置，避免產生局部最優解。

算法2本文所提IGW-CNI 算法

輸入圖G=(V,E)，種子集規模k，群體規模n，迭代周期maxt

輸出集合，不同參數下的種子集S

在本文所提IGW-CNI 算法中，利用隨機位置函數生成基本解i（狼i的基本位置Xi及其對應的種子節點集Si），該函數的運行機制如文獻[13]所提算法所示。其中，給每個節點vj V′∈ 賦隨機值Xi,j，并將該隨機值作為該節點被選為種子節點的概率，且該概率與節點的影響力成正比。在本文所提IGW-CNI 算法中，根據α、βγ、狼的位置來更新δ狼的位置，以期獲得更優位置。故基于此設置了更新位置函數，該函數進程如文獻[12]所提算法所示。其中，為更新節點vj在狼i，即Xi,j中的概率，參考了該節點為α、β、γ的位置Xi，可計算Y1、Y2、Y3的值，并相應計算Xi,j(t+1)的值。通過計算每個節點v j∈V'的Xi,j(t+1)值，將迭代周期t+1內狼i的位置更新為Xi(t+1)，并更新Xi中的Xi,j，以對每個Xi,j(j∈1,…,|V′|)，都在多次迭代中更新狼i的位置，重復此計算可更新每次迭代中狼的位置。

4 數值算例

4.1 數據說明與參數設置

為證明本文所提IGW-CNI 算法的有效性，本文使用4 個真實復雜網絡數據集進行數值模擬，以便觀察算法對現實情況的適應度（實驗中使用的真實復雜網絡數據集特征如表1 所示）。其中，激活率為節點激活概率，根據網絡圖的稀疏性進行設置，并基于網絡節點度和二階度的平均值進行計算。本文使用Python 軟件以近期的熱點事件“HUAWEI event”和“華為事件”的30 個熱點評論節點作為初始節點，分別爬取Facebook、Twitter、新浪微博和豆瓣的復雜網絡節點數據集作為仿真實驗的基礎數據集（爬取時間為2020 年4 月23 日至2020 年11 月16 日）。本文將每個節點作為一個節點，使用節點間的邊界表示節點間的關系。本文選擇了10 個具有較強影響力的節點及其鄰節點列表作為復雜網絡初始節點，以此生成了簡單復雜網絡。實驗在MATLAB 2017b 環境下實施，并在Windows10操作系統的服務器（Intel Xeon 處理器（34 GHz）和32 GB 內存）上進行。

表1 復雜網絡數據集說明

為評估本文所提IGW-CNI 重要節點識別算法的性能，將其結果與現有較成熟的重要節點識別算法進行比較，其中包括 Node2vec[17]、PageRank 法[28]、度遞減搜索策略（DDSE,degree descending search strategy）[23]和模擬退火EDV 值（SADV,simulated annealing EDV）[35]。由于實驗中IGW-CNI 重要節點識別算法預測列表在每次運行時的結果都可能不同，故設置評估結果為迭代100 次運行后的平均值，運行的平均標準差為1.524。首先，本文對所提IGW-CNI 算法參數對適應度函數值的影響進行分析，得到了節點規模和迭代周期的最優值。為分析迭代周期的影響，設迭代周期的取值范圍為[0,50]。在適應度函數值為[10,20,30,40,50]的情況下，各網絡數據集中的實驗結果如圖1 所示。由圖1 可知，當迭代周期超過20 時，適應度值沒有顯著增加，故在后續實驗中將maxt設為20。

圖1 不同迭代周期下的適應度值

本文還對節點規模與適應度值間的關系進行研究，設迭代周期的取值范圍為[0,50]，并計算當種群適應度函數值為{10,20,30,40,50}時不同節點規模下的適應度值，結果如圖2 所示。由圖2 可知，適應度值隨著節點規模的增大而增大，但當節點規模大于20 時，適應度值沒有顯著增加，故將節點規模固定為20。

圖2 不同節點規模下的適應度值

4.2 實驗結果

本節對所提算法的收斂速度進行了研究，并研究了優化過程中的狼群運動，計算了2 次連續迭代t和t+1 中狼i位置間的歐氏距離。而所有類似的狼在連續2 次迭代t和t+1 中的平均移動（AM,average movement）為

其中，n表示節點規模。實驗結果如圖3 所示。由圖3 可知，在初始迭代中的平均運動增加，隨著迭代次數的增加，平均移動次數收斂。盡管在最終迭代中存在振蕩行為，避免了算法陷入局部最優解，但所提算法最終會呈收斂趨勢。

圖3 不同復雜網絡中平均移動分析結果

本文對所提IGW-CNI 算法與其他重要節點識別算法的性能進行比較。為此，將種子節點集的規模定義為[0,50]，并對種子節點集的影響力進行評價，相關結果如圖4 所示。由圖4 可知，與其他算法相比，本文所提IGW-CNI 算法具有較好表現，且在種子節點數量相同的情況下影響力較大，這是由于隨著種子節點集規模的增加，種子節點間的距離也發揮重要作用，故IGW-CNI 算法比其他算法所選擇的種子節點集具有更高的影響力，即本文所提算法在不同種子集規模下都優于其他算法。隨著種子集規模的擴大，本文所提算法得到的種子集影響力的增長速度快于其他算法，這是由于IGW-CNI 算法利用改進灰狼優化算法來進行種子集估計并利用隨機位置函數生成基本解，因此得到的種子集規模較其他經典算法會具有更快的增長速度。

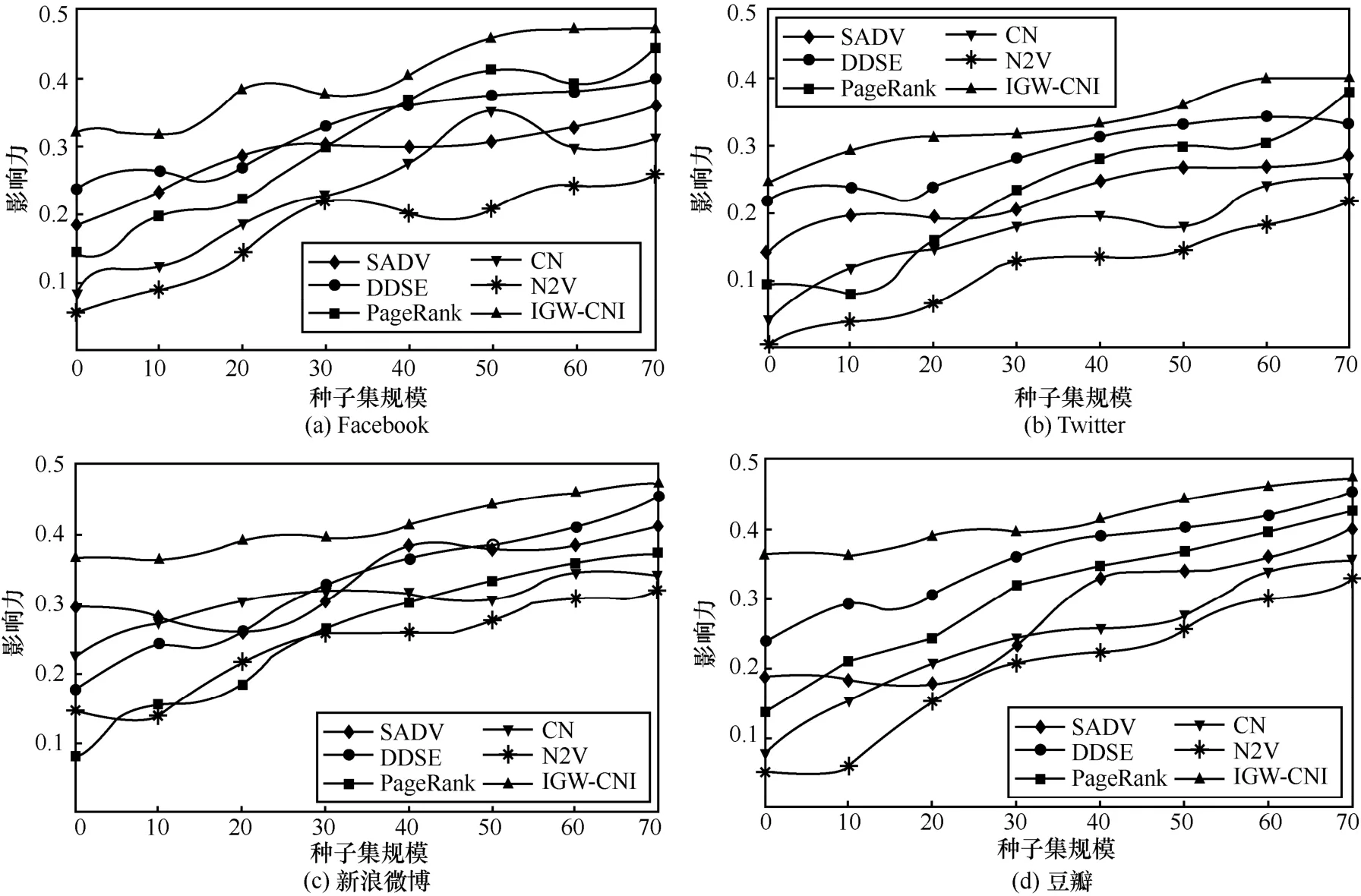
圖4 不同復雜網絡中種子集規模對影響力的算法比較結果

本文進一步改變IC 模型的激活率以分析其對算法性能的影響。為此，將k值設為30，激活率值設置為區間[0,0.2]，間隔為0.005。結果如圖5 所示，隨著p值的增大，節點集的影響力也隨之增加。本文所提IGW-CNI 算法的性能在大多數情形下較其他算法為最優，且隨著p值的增大，其優勢更加突出。這是由于節點影響力隨著p值的增大而增大，而在適應度函數中應用熵函數可使IGW-CNI 算法選擇重疊較少的種子集，故本文所提IGW-CNI 算法在激活率較高時方面優于其他算法，即本文所提IGW-CNI 算法在不同p值下都優于其他算法，且隨著激活率p值的增大，本文所提算法得到種子集的影響力的增長速度快于其他算法。

圖5 不同復雜網絡中激活率對影響力的算法比較結果

本文使用如式(12)所示精度計算方法進一步進行算法比較。

其中，真正例（TP,true positive）表示正確預測鏈接的數量，真負例（TN,true negative）表示正確的未預測鏈接的數量，假正例（FP,false positive）表示錯誤預測鏈接的數量，假負例（FN,false negative）表示錯誤的未預測鏈接的數量。

算法精度比較結果如表2 所示。由表2 可知，本文所提IGW-CNI 算法在不同數據集中都優于其他重要節點識別算法，這是由于本文將影響最大化問題建模為具有成本函數的優化問題，并采用改進灰狼優化算法加以解決，有效提升了算法精度。在Facebook 數據集中，PageRank 與DDSE法的性能僅次于本文所提IGW-CNI 法，這是由于在聚類系數較高、激活率較低的情況下，PageRank 與DDSE 法都考慮了入鏈數量的變化，故計算精度相對較高；在 Twitter 數據集中，SADV 法的性能僅次于本文所提IGW-CNI 法，這是由于在平均度與激活率較高的情況下模擬退火算法可更好地加速收斂過程，因此可以得到相對較優的計算精度結果；在新浪微博數據集中，N2V 和 CN 法的性能僅次于本文所提IGW-CNI 法，這是由于在平均路徑較大的情況下，基于網絡圖最短路徑進行鄰節點度計算可有效提升算法計算精度。

4.3 統計檢驗

本文在此對測試算法性能的統計顯著性差異進行進一步分析。為取得統計顯著性，進行了Friedman檢驗，使用Bonferroni法來校正實驗結果[36]，并設置可信度分數為α=0.05，這表明如果p<0.05，則存在差異顯著。表3 中，本文所提IGW-CNI 算法將成本函數表示為節點影響力及其間的距離，并使用Shannon 熵對節點影響力進行度量的優勢較其他經典算法會充分體現。Friedman 檢驗對AUC 的觀察檢驗值Ff為54.142，均大于相應的χ2值（即χ2(αc,Df)）。當置信區間α=0.05、自由度Df=8時，χ2值為15.51，故拒絕零假設。

表3 對AUROC 值的Friedman 統計檢驗結果

4.4 大數據集實驗

為檢驗本文所提IGW-CNI 算法在極限條件下的適用性，本節使用規模更大的 MovieLens 20M、DatingT 和Netflix 等復雜網絡數據集對上述重要節點識別算法進行對比實驗，以進一步分析本文所提算法在大數據集中的適用性（其中MovieLens 20M 和Netflix 數據集常用于推薦算法研究，且呈現包含節點和目標2 種節點的二部圖網絡結構，但本文所提算法更加重視在網絡環境下的應用，故在上述2 種數據集中只采用節點以進行大數據集實驗。這也從另一角度對本文所提IGW-CNI 重要節點識別算法在二部網絡圖中的適用性進行分析，進一步證實了本文所提算法的普適性）。其中，MovieLens20M 被國內外學者認為是最穩定的基準數據集之一，其包含139 428 個節點對27 493 部影片的20 351 902 條評分；DatingT 數據集包括136 739 名男性和179 332 名女性組成的18 293 016 條交友記錄；Netflix 數據集中包括480 189 個節點對17 770 部電影的100 480 507 條評分記錄。圖6 給出了同等參數條件下上述3 種大數據集中的算法比較結果。由圖6 可知，在體量更大的數據集中的實驗結果基本與圖5 中的實驗結果一致。此外，本文還使用上述3 種大數據集作為對照組重復進行了精度與效率等方面的實驗，結論與前文一致，故在此不再贅述。

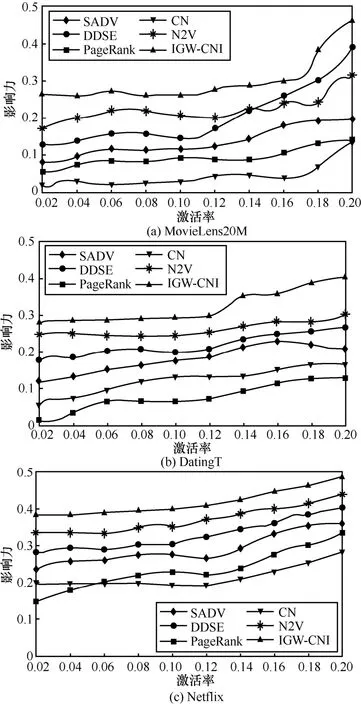
圖6 不同大規模復雜網絡中激活率對影響力的算法比較結果

4.5 時間復雜度

最后，本文對所提IGW-CNI 算法的計算時間復雜度效率進行了分析，并對算法的平均運行時間進行了比較，結果如表4 所示。由表4 可知，本文所提IGW-CNI 法的效率高于其他算法，且獲得的種子節點集的影響力性能更優。

表4 時間復雜度實驗結果

5 結束語

復雜網絡中的重要節點識別對電子商務、網絡營銷等多個領域都有很大影響。在預算有限的情況下，網絡營銷所面臨的一個主要挑戰是識別少數具有影響力的重要節點集，即種子節點集，以期通過將信息傳遞給種子節點集在復雜網絡中獲得較大影響力，故可將此問題轉化為節點影響最大化問題。本文將影響最大化問題建模為具有成本函數的優化問題，并采用改進灰狼優化算法解決此問題。最后基于真實復雜網絡數據集進行比較實驗，結果表明，本文所提IGW-CNI 算法優于其他影響力最大化算法，不僅效率更高，計算時間也短。

盡管本文已提出了上述具有重要意義的發現，但還具有一定局限性，其中一些可能會為未來的進一步研究指明方向。首先，本文所提改進灰狼優化算法為基于種群的優化算法，仍可能存在局部最小值，可考慮引入隨機梯度等方法避免出現局部最小值。其次，可結合社會化調查法和計算實驗等研究框架對所提重要節點識別算法進行進一步佐證。最后，可嘗試使用如自編碼器等深度學習方法進一步提升重要節點識別算法的效率和精度。