超長距10G光傳輸系統帶內四波混頻現象研究

張 菡，熊 鋮，李 由

(貴州電網有限責任公司信息中心，貴州 貴陽 550003)

超長距光纖通信是一項發展成熟的技術，目前10G 同步數字體系(Synchronous Digital Hierarchy，SDH)技術已在超長距光通信傳輸網絡中大量應用。隨著社會需求的增加以及5G 技術的蓬勃發展，對光通信傳輸系統容量和無電中繼傳輸距離的要求越來越高，信道間距越來越小，單信道入纖功率越來越高，這使得光纖中的非線性效應對光傳輸系統的影響越來越大[1－4]。因此定量分析光傳輸系統中各非線性效應對系統性能的影響程度對于系統的優化設計具有重要的意義。

四波混頻效應(Four Wave Mixing，FWM) 由Stolen 等人首次發現[5]，是一種重要的三階非線性效應。此效應會產生新的光場，并造成信號功率的損耗，對系統產生非線性串擾，且在高入纖功率下尤為明顯，因此大大限制了光傳輸系統的傳輸容量和傳輸距離[6－7]。目前已有大量關于FWM 效應產生的物理機制以及理論模型的研究成果可供參考[8－12]。例如金泓等人[9]發現四波混頻效應在密集波分復用系統(Dense Wavelength Division Multiplexing，DWDM)中造成不同信道內信號相互之間的干擾；關雅莉等人[11]研究了光纖傳輸過程中四波混頻和色散之間的互相影響；張鵬等人[12]論證了光纖傳輸過程中四波混頻對受激拉曼散射效應造成的影響。現有對FWM 效應的研究中，大多集中于此效應對波分復用系統 (Wavelength Division Multiplexing，WDM)乃至DWDM 系統的影響，而對于單個信道內的FWM 效應關注較少。本文研究中發現，在大功率長距離光傳輸系統中，帶內信號與10G 調制信號的相位匹配會導致帶內四波混頻效應的產生，并在輸出端光譜中觀察到明顯的譜肩的出現，此現象在入纖功率升高時尤為顯著，并進而成為限制光傳輸系統傳輸功率的主導機制。

本文基于簡并FWM 理論進行研究:利用仿真軟件建立光傳輸系統數值模型，進行數值計算并與實驗數據擬合，量化FWM 效應對光傳輸系統的限制作用，并進而提出抑制此限制效應的方法。此外，自相位調制(Self-Phase Modulation，SPM)和群速度色散(Group Velocity Dispersion，GVD)效應也同時在光傳輸系統模型中考慮，并在光譜仿真結果中有所體現。

1 實驗系統架構

本研究中的實驗系統采用商用光傳輸模塊搭建，其系統框架如圖1 所示。

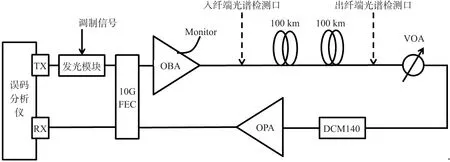
圖1 實驗系統框圖

圖中10G SDH 誤碼分析儀發送并同步接收10G 單波信號，以分析光傳輸系統的誤碼率。發送信號首先經過一個10G 小型可插拔(10 Gigabit Small Form Factor Pluggable，XFP)光模塊，此光模塊基于光－電－光(Optical-Electrical-Optical，OEO)轉換實現對信號非線性效應的優化及直接調制。隨后信號經由10G 前向糾錯編碼器并被EDFA 光放大器(Optical Booster Amplifier，OBA)放大后進入200 km的G652 光纖及光衰減器，調節衰減器可等效延長光纖距離。出纖信號經過色散補償模塊(Dispersion Compensation Module，DCM)以及摻鉺光纖放大器(Erbium-Doped Fiber Amplifier，EDFA)光預置放大器(Optical Power Amplifier，OPA)放大后返回誤碼分析儀。此系統的觀測口置于光纖前端和后端，用于觀測入纖和出纖的信號光譜。實驗中系統導通條件下所測試的數據均驗證12 h 以上無誤碼。

2 實驗結果

在實驗測試過程中我們首先觀察了XFP 光模塊對系統傳輸距離以及光譜的影響。XFP 光調制技術使得超長距無中繼光傳輸系統能夠實現，目前已廣泛應用在光傳輸系統中。以本文搭建的系統為例，當XFP 光模塊關閉時，系統的受激布里淵散射(Stimulated Brillouin Scattering，SBS) 閾值只有4 dBm，這樣的功率限制顯然無法滿足超長距無中繼的要求。當XFP 光模塊開啟時，系統的SBS 閾值可以達到17 dBm 以上，這極大地提高了傳輸信號的功率，光纖傳輸距離最高可達220 km，這也使得光纖傳輸系統可以滿足超長距無中繼的要求。

在改變入纖光功率時持續觀測出纖光譜時發現，隨著入纖光功率提升，在信號光譜兩邊逐漸出現了明顯的譜肩，圖2 為入纖光功率為21 dBm 時的入纖(經20 dB 衰減)和出纖光譜。

而對比觀測光模塊關閉時的出纖光譜，譜肩消失，如圖3 所示。說明譜肩出現主要是由于光模塊中調制光的影響。光模塊中的調制信號為10G 調制光，因此在光譜圖中體現為在信號光譜中心波長±0.08 nm 處疊加兩個光譜。但信號光本身具有一定的展寬，因此調制光譜被淹沒在信號光譜中。而信號光在光纖傳輸過程中由于信號光和2 個調制光的頻率恰好符合相位匹配條件，從而產生帶內簡并FWM 效應，在信號光中心波長±0.16 nm 處產生兩個新的四波混頻光，這兩個光譜離信號光譜較遠，因此疊加后出現如圖2(b)中的譜肩。

圖2 XFP 光模塊開啟時輸入端和輸出端光譜

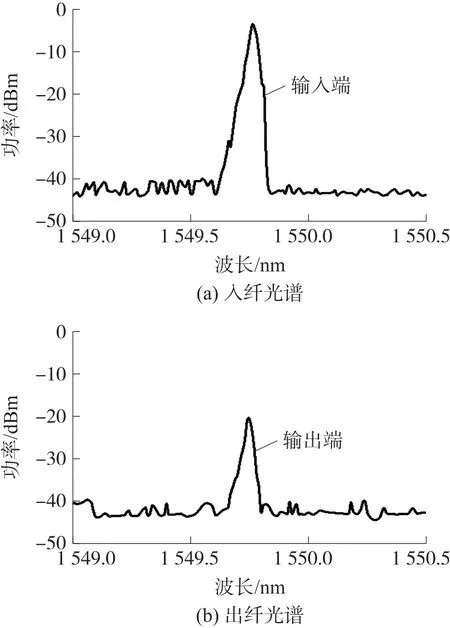
圖3 XFP 光模塊關閉時輸入端和輸出光譜

3 理論模型與分析

3.1 數值仿真模型

3.1.1 FWM 理論模型

四波混頻光是由至少三個不同波長的光波在同一根光纖中同時傳輸時所產生的，由于有新的光頻出現，會嚴重地影響信號的傳輸質量。四波混頻效應的產生要求同時滿足凈動量守恒和凈能量守恒。凈能量守恒需滿足頻率條件ω1＋ω2＝ω3＋ω4，而凈動量守恒需滿足相位匹配條件Δk＝0，即[10]:

式中:Δk為相位失配因子；k為波矢。

當一強光束在光纖中傳輸時，介質會感應非線性極化而產生非線性效應。基于光場的非線性理論，可推導光纖中傳輸過程中四波混頻光的理論公式。在本研究中，入纖信號與2 束關于信號中心頻率對稱的10G 調制信號組成3 個滿足相位匹配條件的光場，因此在響應的倍頻點產生2 束四波混頻光。由于只考慮不同頻率的產生只在小間隔內發生，因此可以忽略由于頻率的變化而產生的三階電極化效應。并且由于產生的四波混頻光功率較低，因此忽略自相位調制和交差相位調制及三次諧波的產生，且初始的三個光場功率變化可忽略。從而產生的四波混頻光功率公式可簡化如下[11]:

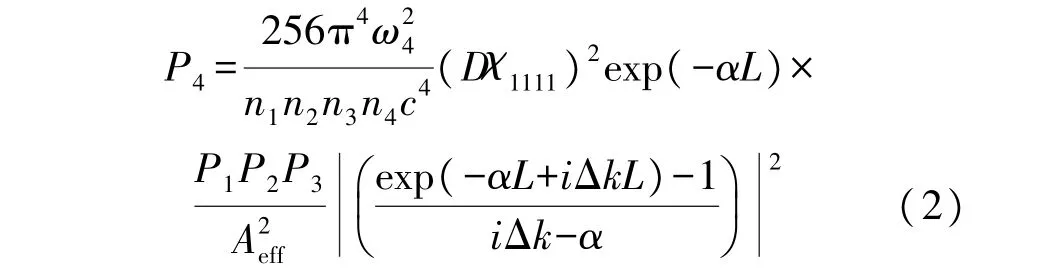
式中:ω4為四波混頻光頻率；n1－n4為光纖折射率，取值1.45；c為光速；因子D可取值1、3 或6，此處取6；χ1111為三階非線性電極化率，取特征值10－13；P1－P3為光脈沖功率；Aeff為光纖有效面積，取特征值50 μm2；α為光纖衰減項，取實測值0.19 dB/km；L為光纖長度。Δk為相位失配因子Δk沿四波混頻光傳播方向上的分量。當相位匹配完全滿足時，即Δk＝0 或Δk＝0 時，可得四波混頻光功率為:

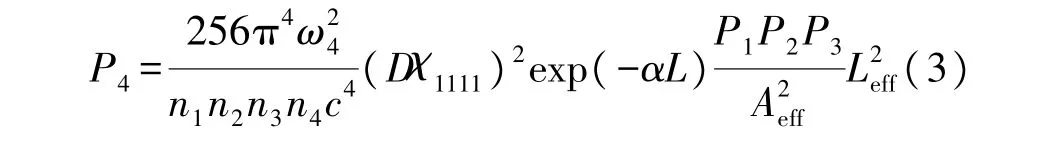
式中:Leff＝[1－exp(－αL)]/α。

3.1.2 非線性方程求解與色散效應模型

當強光場在光纖中傳輸時，介質對光的響應呈非線性，此類效應包括SBS、自相位調制(Self-Phase Modulation，SPM)、交叉相位調制(Cross-Phase Modulation，XPM)、FWM 等。此外光纖中色散效應是入纖信號與光纖中電介質的電子的相互作用，通常表現為光纖的折射率與光波頻率ω有關。基于Maxwell 方程，考慮到光纖的色散和非線性效應，可推導出光波在光纖中傳輸的非線性薛定諤方程[13]:

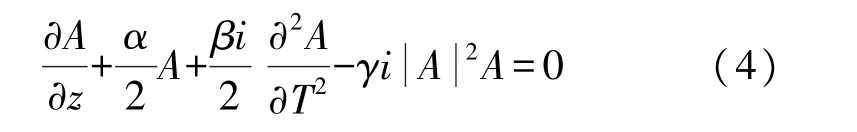
式中:A為信號脈沖振幅；z為光傳輸距離；β為群速度色散；T為時間；γ為非線性系數。

以上推導的非線性薛定諤方程是非線性偏微分方程。而對此類方程一般無法直接求出解析解，所以需要數值方法來求解。一般情況下，采用分步傅里葉變換法和有限差分法來求解方程。本文采用分步傅里葉變換法來對非線性薛定諤方程求解。

光脈沖信號在光纖中傳輸，會同時受到光纖的色散和非線性效應的作用，對光脈沖的脈寬、頻譜產生影響。分步傅里葉變換法的思想就是將光纖總傳輸距離分解為若干段較小的距離h，對于每段距離h可以分別計算色散和非線性效應對脈沖的影響，最后得到近似結果。具體就是當光脈沖在光纖中傳輸了h/2 時，此刻只考慮色散的作用；然后在z＋h/2 處考慮非線性的作用；最后當光脈沖繼續傳輸h/2 以后考慮色散效應，得到傳輸距離為h近似解。最后將兩部分的結果相乘，就得到光脈沖信號在光纖中傳輸距離h時的近似解。通過這種分步傅立葉數值算計算的方法，求解信號在各段h距離中的非線性薛定諤方程。

通過公式推導，得到在h/2 距離中GVD 公式為[13]:

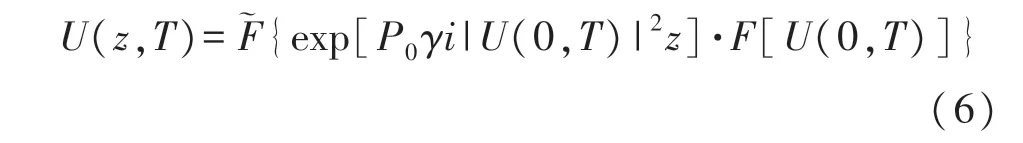
本文基于以上模型，利用MATLAB 對光纖中各段距離迭代，得到出纖信號的非線性薛定諤方程的數值解。其中，非線性效應主要描述SPM 效應。

基于以上FWM 理論和分步傅里葉變換法，我們建立了信號光在光纖中傳輸的數值仿真模型。

3.2 仿真結果分析

我們基于前部分內容介紹的仿真模型進行了數值驗證，并調整相關參數擬合實驗結果，仿真結果如圖4 所示。

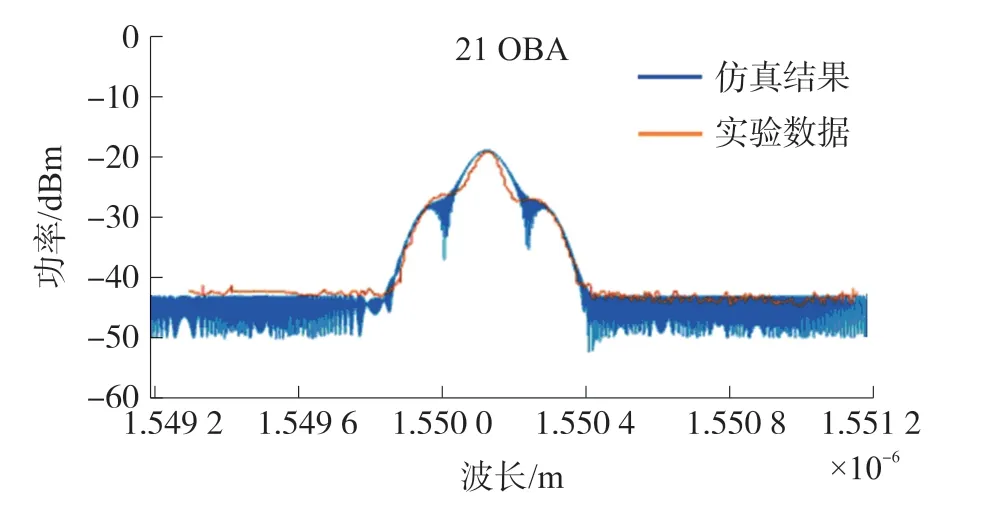
圖4 考慮帶內FWM 效應的出纖光譜仿真結果與實驗數據對比

圖中仿真結果與實驗結果擬合度較高，且譜肩出現位置與實驗結果吻合，驗證了帶內FWM 效應為出現譜肩的主要機制。

隨后，我們對譜肩功率變化的影響因素進行了深入研究。譜肩出現的主導機制為入纖信號與調制信號的帶內FWM 效應，因此譜肩功率也主要與入纖信號功率和調制信號功率相關。當調制信號功率保持不變，入纖信號功率逐漸上升時，實驗結果和仿真結果均表明譜肩功率逐漸上升且譜肩功率與光譜峰值功率比值逐漸降低，如圖5 所示。

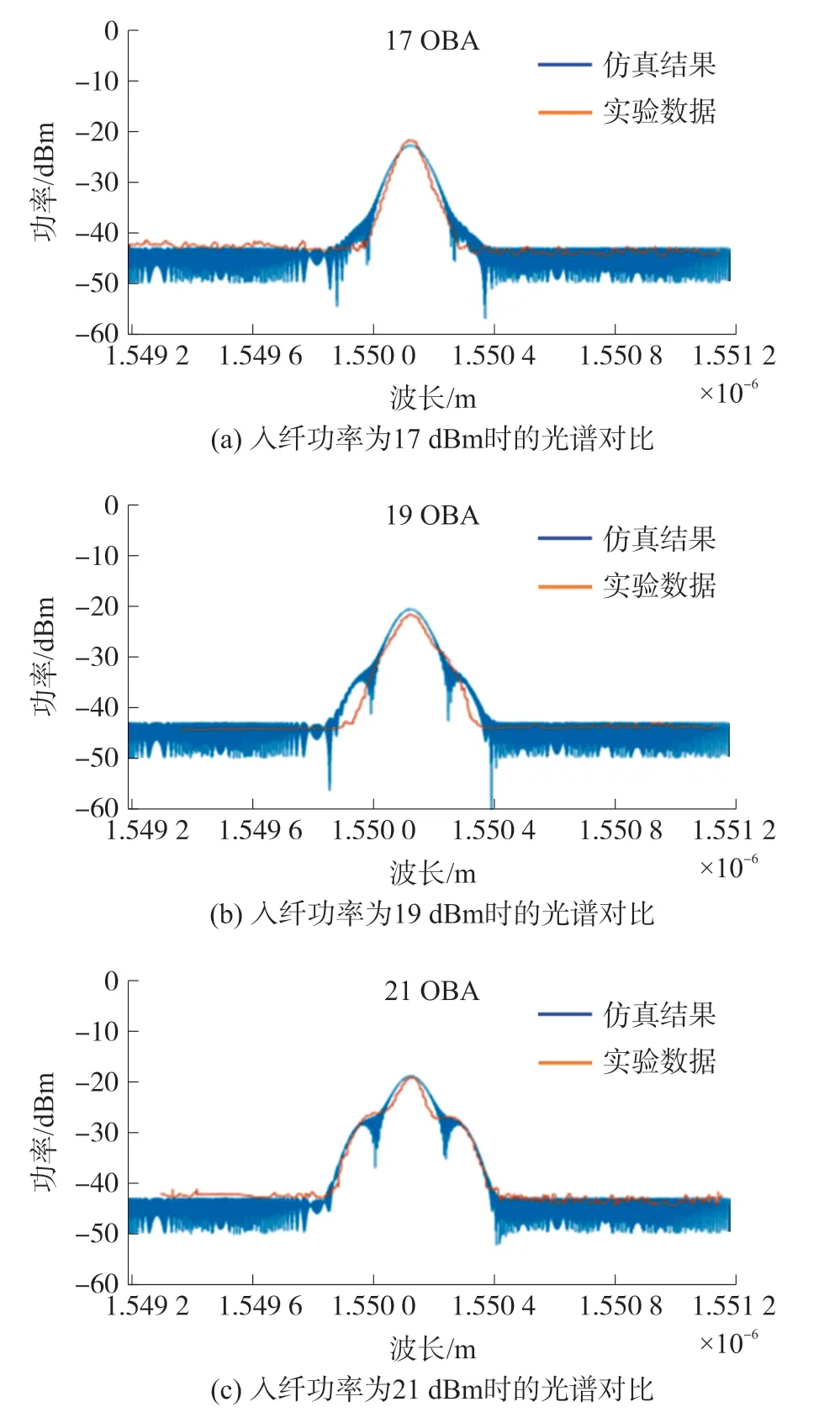
圖5 不同入纖信號功率的輸出端實驗光譜與仿真光譜對比

為定量分析帶內FWM 效應對系統無電中繼最大傳輸距離的影響，我們進而將測試光纖替換為多段短距離光纖以分段檢測信號光譜在傳輸過程中的變化情況以及對系統的影響。測試中采用5 段20 km G652 光纖以及2 段50 km G652 光纖替代原本的200 km 光纖，并在分段處接入OSA 觀測光譜變化，并斷點接入FEC 回路測試系統導通情況。當入纖信號功率為21 dBm 時，入纖處、20 km 處、40 km處以及60 km 處的信號光譜如圖6 所示。可以看出在40 km 處信號光譜開始出現顯著譜肩，且此時接入系統回路，系統已無法導通。分析是由于此時光譜譜肩出現，信號接收端認定譜肩為噪聲電平。因此譜肩的出現將導致等效OSNR 大幅降低，并低于接收端極限，從而系統無法導通。而從測試結果中可以發現，當入纖信號功率為17dBm 時，輸出端無明顯譜肩出現，最大傳輸距離可達220 km 以上，而當入纖信號功率為21 dBm 時，由于帶內FWM 效應的影響，在光纖距離40 km 以內就出現明顯譜肩，即系統無電中繼最大傳輸距離驟降至40 km 以下，完全無法滿足實際應用需求。

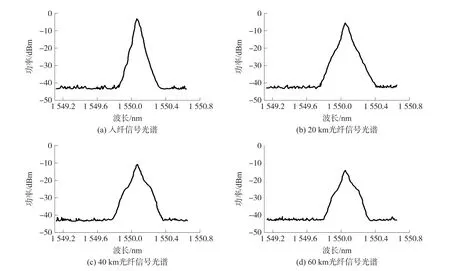
圖6 入纖信號功率為21 dBm 時光纖中各段距離處的信號光譜對比

4 影響和討論

在先前測試中我們發現，誤碼分析儀會選取光譜峰值功率與譜肩功率比值作為等效的OSNR，這個等效OSNR 將成為限制最大入纖光功率的重要因素。已知XFP 光模塊的調制信號功率越高，對SBS效應的抑制效果越明顯，即SBS 閾值越高。為了提高傳輸功率，從而提升無電中繼傳輸距離，可進一步提高調制信號功率以提升SBS 閾值，然而過高的功率會導致等效OSNR 低于光探測器極限，因此，入纖信號功率、調制信號功率由于帶內FWM 和SBS 等非線性效應相互制約，無電中繼最大傳輸距離存在極限。

目前通過XFP 模塊的優化設計，可將光傳輸系統的SBS 閾值提升至17 dBm 以上，而進一步提升SBS 閾值是眾多研究者的研究方向，也是技術發展的必然趨勢。當入纖信號功率進一步提升時，帶內FWM 效應對光傳輸系統的影響將逐漸顯現并成為制約無電中繼最大傳輸距離的主要因素。而基于本文所建立的傳輸系統數值模型，在確定OSNR 極限以及XFP 光模塊的物理參數后，可精確計算最大傳輸功率，為光傳輸系統的設計提供理論預測。

此外，針對帶內FWM 效應的抑制技術將有望進一步提升無電中繼最大傳輸距離。第一種方法是降低調制信號功率。基于四波混頻效應理論，降低調制信號功率可降低四波混頻光功率，從而降低譜肩功率，抑制其對接收端OSNR 的影響。第二種方法是采用光譜整形技術。光譜整形技術如平方根升余弦脈沖(Square Root Rising Cosine Pulse，RRC)、M型平方根脈沖(Root M-shape Pulse，RMP)和隨機脈位調制(Radom Pulse Modulation，RPP)等可通過調整光譜高頻部分和低頻部分的功率分量，展寬光譜帶寬，從而破壞相鄰光譜之間的相位匹配條件，抑制四波混頻效應。因此對輸入信號以及調制信號進行光譜整形可抑制信號光譜譜肩的產生。第三種方法是采用相干光通信系統。相干光通信主要利用相干調制和外差檢測技術。所謂相干調制，指利用要傳輸的信號來改變光載波的頻率、相位和振幅；所謂外差檢測，指將一束本機振蕩產生的激光與輸入的信號光在光混頻器中進行混頻，得到與信號光頻率、相位和振幅按相同規律變化的中頻信號。采用相干光通信系統即使出現帶內四波混頻效應導致信號光譜譜肩的出現，系統仍能夠檢測出有效信號，因此此時信號光譜變形導致的OSNR 降低不會影響系統信號檢測及工作性能。

5 結束語

本文深入研究了超長距光傳輸系統出纖端光譜出纖譜肩的現象，通過理論分析和數值仿真論證了此現象主要來源于入纖信號與XFP 光模塊所產生的調制信號之間的帶內FWM 效應。此現象導致等效OSNR 的產生，且隨著光傳輸功率的升高，等效OSNR逐漸降低，因此限制了入纖信號功率的進一步提升。此外，本文還提出了三種針對帶內FWM 效應的抑制技術，將有望進一步提升無電中繼最大傳輸距離。