三軸循環荷載下飽和板巖的滯后特性研究

榮 笛，孟陸波

(1.成都理工大學環境與土木工程學院，四川 成都 610059; 2.成都理工大學 地質災害防治與地質環境保護國家重點實驗室，四川 成都 610059)

0 引 言

在深基坑工程中常常遇到沖擊荷載、地震等動荷載作用，這些工程的施工建設往往和巖體打交道，在施工設計中一般認為巖體為剛體或者彈性體，從相關研究可以了解到巖石同時具有彈塑性，在動荷載作用下巖石會發生彈性變形與塑性變形出現非線性滯后特性，研究巖石在高應力條件下的動荷載變形演化規律以及強度變化對保證工程施工的順利進行和人員安全有著重要的研究意義。

在1965年COOKNGW和HODGSONK[1]首先發表了巖石的滯后現象后的論文后，研究人員對巖石滯后現象的研究就從未停止過腳步，BRENNANBJ和MCKAVANAGHB[2-3]的研究結果表明，當應變為10-5～10-3范圍內時，應力-應變滯后曲線會出現尖點，而當應變為10-6滯后回線呈橢圓；劉建鋒、任浩楠、聶明等[4-6]針對于巖石進行循環加卸載試驗，發現在加卸載過程中動應變相位都滯后于應力相位，滯回環在荷載反轉處并非橢圓形而是尖葉狀；肖建清[7]在后續的試驗中發現在循環卸載階段，應變相位滯后于應力相位，而在加載階段應變相位可能滯后、相等或超前于應力相位，并由此提出了滯回環可能形狀、彈性模量優化計算公式等。

關于滯后特性的數據分析與影響因素的探討也有眾多學者做出了研究成果，席道瑛[8-9]等研究了不同種類的飽和巖石在不同頻率下的循環加載試驗，驗證了瞬時彈性模量與應變成不對稱蝴蝶結形的結論，并提出以蝴蝶結張角與交點位置來衡量巖石的滯后程度；陳運平[10-12]進而從蝴蝶結“X”形的切線模量出發，提出了曲線張角與巖石的耗散角有確定性關系，表明切線模量曲線的夾角與其耗散角在衡量巖石的滯后方面具有同等價值；楊小彬[13]開展砂巖不同圍壓下軸向循環加卸載試驗，引入耗能比反映試樣變形演化過程中的能量轉化關系及損傷演化程度，并表明隨著圍壓的增大,耗能比整體呈現減小趨勢；陳釩[14]研究了泥巖的滯回曲線特征與泥巖的黏彈性特性、塑性變形及壓密的難易程度有關。

國內外的研究表明滯回曲線的形狀存在著許多類別，在其滯后現象中大部分學者對卸載階段的應變相位滯后于應力相位表示認同[15]，而對于加載階段應力應變相位滯后現象卻有著不同的說法，有人認為在加載階段應變相位滯后于應力，有人認為幾乎相等，還有人則認為應變超前于應力相位[16]。這些學者從多個角度分析產生此現象的原因，從他們的研究成果中可以了解到造成此現象的因素是復雜多樣的，介于眾多學者的試驗巖樣種類各異，本文結合高地應力條件的工程背景，選擇了某深基坑工程含水巖層的板巖作為試驗對象，進行三軸循環動荷載試驗，進一步探討巖石在加載階段的滯后特性。

1 試驗概述

巖樣采用某深基坑工程含水巖層中的板巖，制成直徑約50 mm，高約100 mm，上下平行角度不超過2.5×10-2mm的圓柱巖樣共12個，分為3組，每組4個。為消除不同巖樣含水率的細小差異可能對試驗結果造成影響，將巖樣飽水處理48 h后，在單軸試驗機上測得平均抗壓強度為126.3 MPa，故循環加載上限值定為接近單軸抗壓強度的70%，即170 kN，下限值為試驗開始準備階段的預壓力值，即2 kN。利用MTS815 Flex Test電液伺服疲勞試驗機系統進行三軸循環試驗。試驗加載方式均為軸向荷載控制，施加的應力均小于屈服強度，圍壓分為三種：5 MPa、10 MPa、15 MPa，每組巖樣分別對應其中的一種圍壓，3組巖樣的圍壓各不相同。試驗準備階段預壓力2 kN，正式加載分為兩個階段，第一階段以從2 kN加載到170 kN，第二階段以170 kN為起點施加循環荷載，加載波形為正弦波，軸向振動頻率為1 Hz，設定荷載加載方式為力加載模式，上限為170 kN，下限2 kN，循環1 500周次，記錄方式為0.02 s記錄一次數據。

2 巖樣的滯后現象

2.1 滯后效應的試驗結果

在剔除數據差異較大的巖樣后，為方便觀察規律，在各圍壓中選取一個數據較穩定、試驗結果最典型的巖樣進行分析，圖1為各種圍壓下第10個循環周次的滯回環，表1為各圍壓下第10個循環周次的滯回環數據表。

表1 第10個循環周次的滯回環數據表

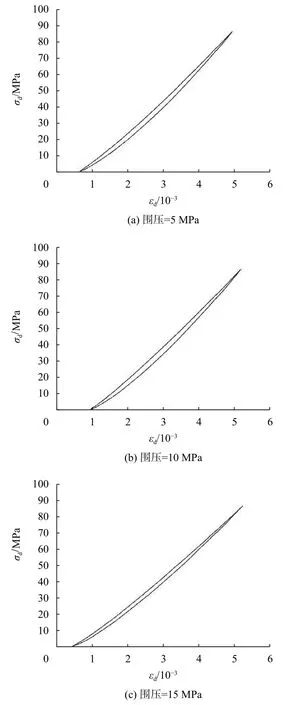
圖1 巖樣的滯回環

為了方便分析，分別取第10、第11、第12次循環數據，運用公式（1）將應力和應變進行歸一化，繪出各圍壓條件下的歸一化的應力-時間曲線和應變-時間曲線如圖2所示。

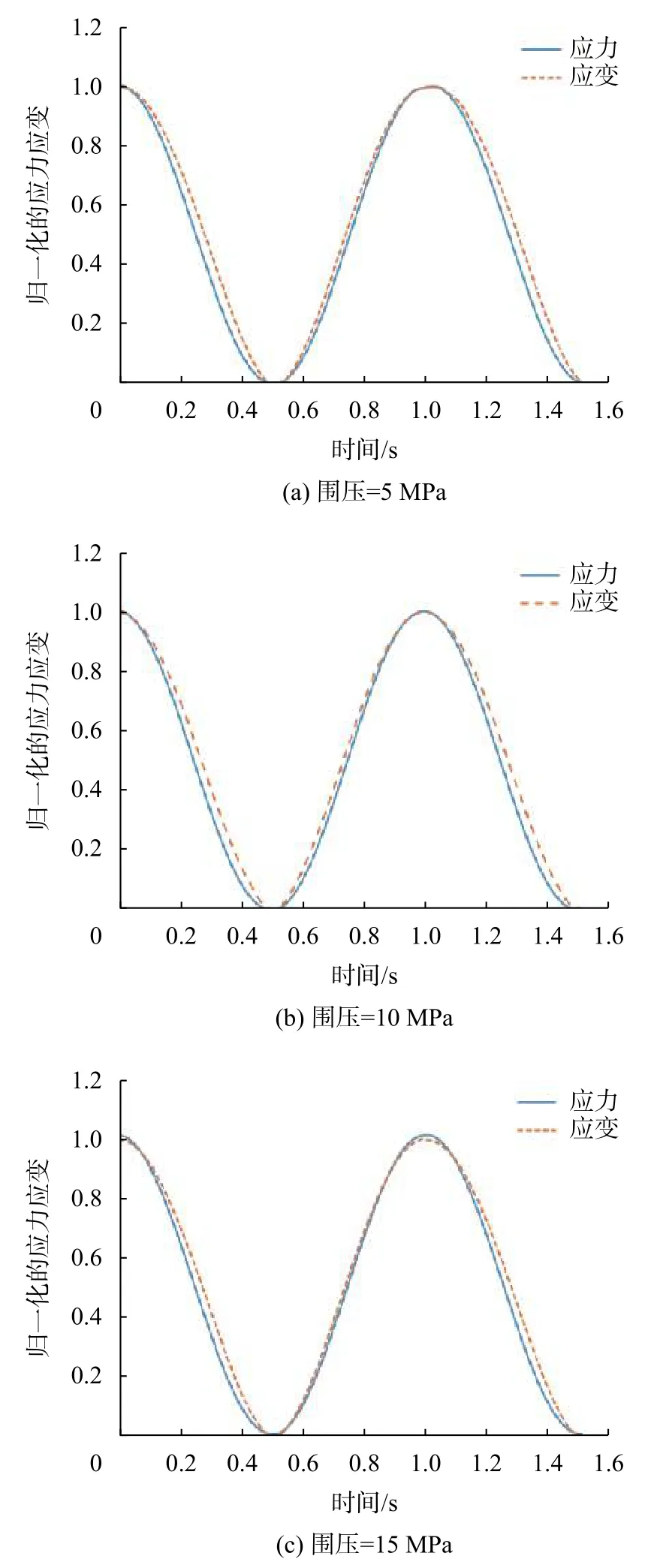
圖2 歸一化后的各圍壓下的應力-時間與應變-時間的曲線

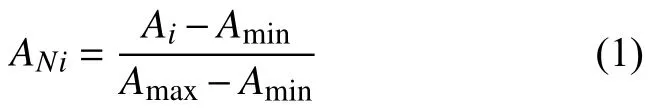
式中：ANi——歸一化后的數據；

Ai——應力或應變原始數據；

Amax，Amin——原始數據中的最大值、最小值。

從圖1可以看出滯回環形狀為上窄下寬的尖葉形，并且隨著圍壓的增加，滯回環面積呈現出減小趨勢。從圖2可以看出，加載階段應變相位略領先于與應力相位，在卸荷階段應變相位明顯落后于應力相位，隨著圍壓的增加，應力應變的相位差逐漸變小。

2.2 滯后性分析

已知一個巖石的應力σ和軸向應變ε，那么該巖石在某點應力處的切線模量E可表示為：

三種不同圍壓下板巖巖樣的切線模量呈現出不對稱的“X”形，這種“X”形切線模量的不對稱性是因為加載和卸載模量的差異所致，這和應力應變滯后性密切相關。從圖3右端b點處可以看出此時發生突變，隨后在某段應變內，卸載曲線相對于加載曲線在相同應變區間段內的數值點個數更多，已知相鄰數值點間隔時間相同，也就是說在產生相同的應變的情況下卸載花的時間比加載時多，由于試驗機荷載加載過程穩定，可以表明應變開始滯后于應力，并在這段區間內應力應變相位差逐漸擴大。

在圖3曲線左端，a點虛線貫穿加載曲線左端的第一個數值點，但卸載曲線左端的第一個數值點卻在虛線的右側，這表明巖樣在回彈過程中產生了應變損耗。以卸載曲線左端第一個點的橫坐標值與加載曲線左端第一個點的橫坐標值的差值代表其應變差，則圍壓5 MPa、10 MPa、15 MPa的兩點的應變差分別為 59.668×10-6、45.637×10-6、42.822×10-6，其第10個滯回環的最小應變分別為0.949×10-3、0.661×10-3、0.369×10-3。如果應變差完全損耗不可復原，即認為在下一個循環開始時應變自動變大，那么隨著循環周次的增加，第1 000個滯回環的最小應變將會是第10個滯回環最小應變的幾十倍，但從圖4得到曲線趨勢表明并不符合上述推論，也就是說應變損耗并不是完全由能量損耗導致，大部分應變差好像自動復原了一樣，巖樣體現了明顯彈性性能。

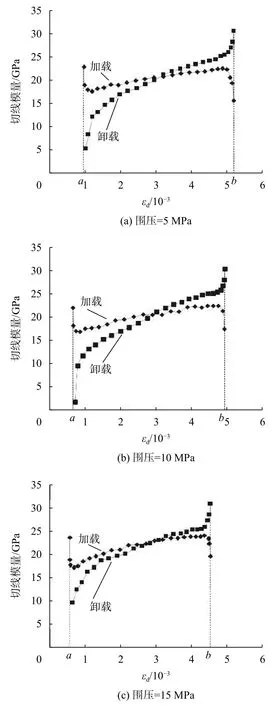
圖3 不同圍壓下的加載和卸載階段的切線模量

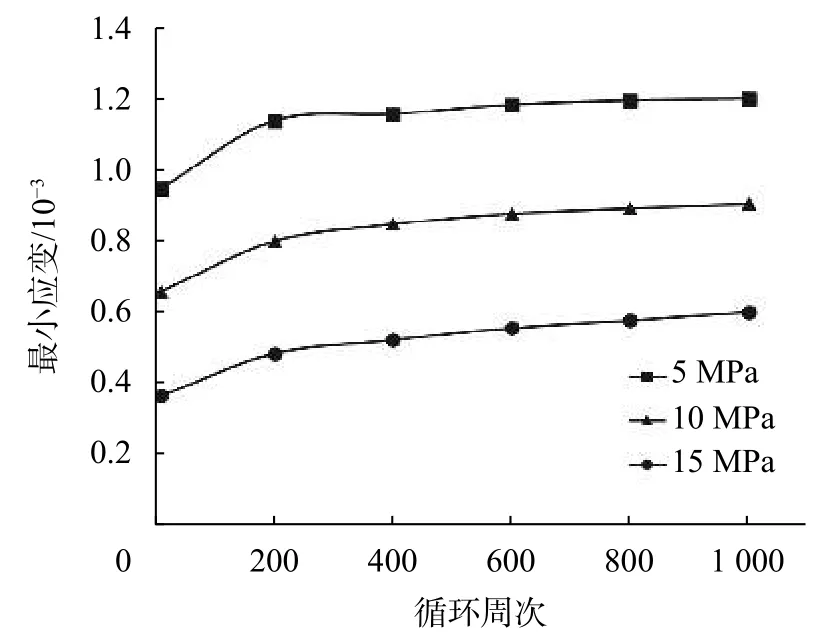
圖4 應變變化曲線

從巖石力學可以了解到在低應力時巖樣更多表現為彈性性能，默認巖樣整體變形，從上述結論可以得出巖樣在此時的能量損耗非常小，這樣在荷載接近最小應力時可以把試樣看成一個線彈性體。

從圖5可以看出，卸載過程中巖樣回彈，巖樣對試驗機上墊塊做功，可以看成巖樣某截面段與上墊塊一起運動，當試驗即將進入下一個循環時，試驗機開始對上墊塊增加荷載，此時可以看成巖樣與上墊塊發生了“撞擊”，由于墊塊剛度遠大于巖樣剛度，墊塊默認不變形，這就好像彈力球撞上鐵板一樣，巖樣與墊塊之間產生了與荷載加載方向相同的反彈力，巖樣在荷載與反彈力共同作用下發生變形，由于巖樣受到反彈力產生的額外變形，所以可能造成在加載階段時應力相位滯后于應變相位，由于此時應力較小導致反彈力小，效果相比于卸載過程時不明顯。由此表明圖3的加載實際起點可能是第2或者第3個數值點，說明最小應力不對應最小應變，事實上在處理試驗數據時也發現了這一現象，這也表明在應力最小值附近滯回曲線不是一個嚴格的尖點。

圖5 試樣回彈過程圖

在圍壓的作用下，可以發現加載與卸載兩條曲線隨著圍壓的增加而靠攏，巖樣內部微裂縫或微裂隙逐漸被壓密，同時圍壓也可以在一定程度上阻止巖樣內部顆粒的滑動，圖2反映了圍壓的增加使應力相位超前應變相位的效果變小，進而說明了圍壓的增加會減小其滯后效果。

3 滯回環與動彈性模量

動應力-動應變滯回環如圖6所示。

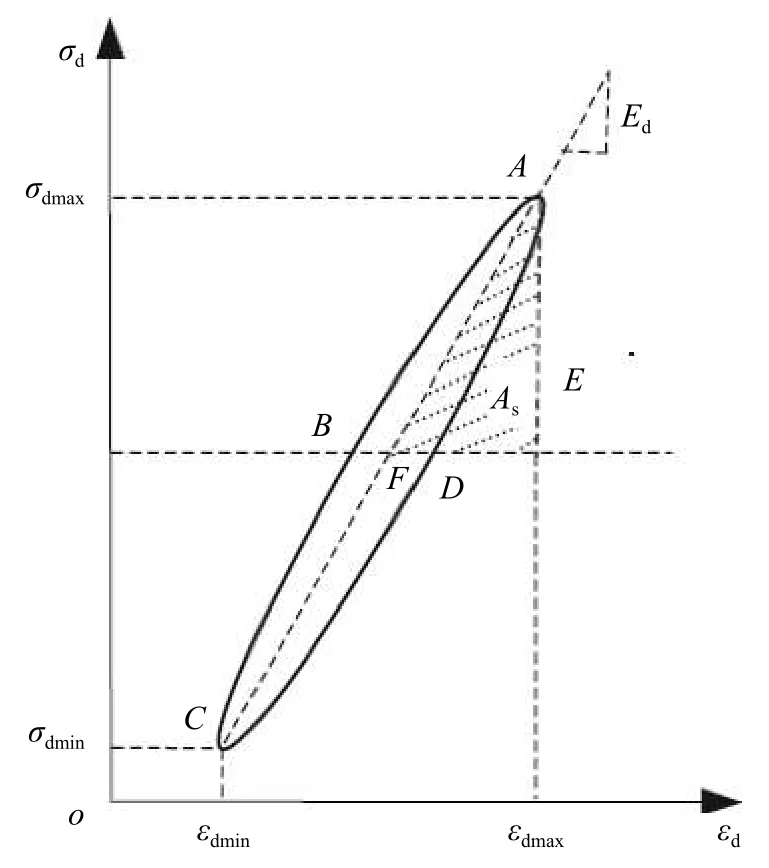
圖6 動應力-動應變滯回環

巖石的動彈性模量一般由下式計算：

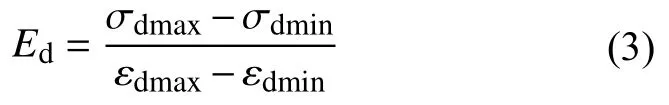
式中：Ed——動彈性模量；

σdmax、σdmin——滯回環中軸向最大動應力與軸向最小動應力；

εdmax、εdmin——滯回環中軸向最大動應變與軸向最小動應變。

巖樣滯回環示意圖如圖7所示。

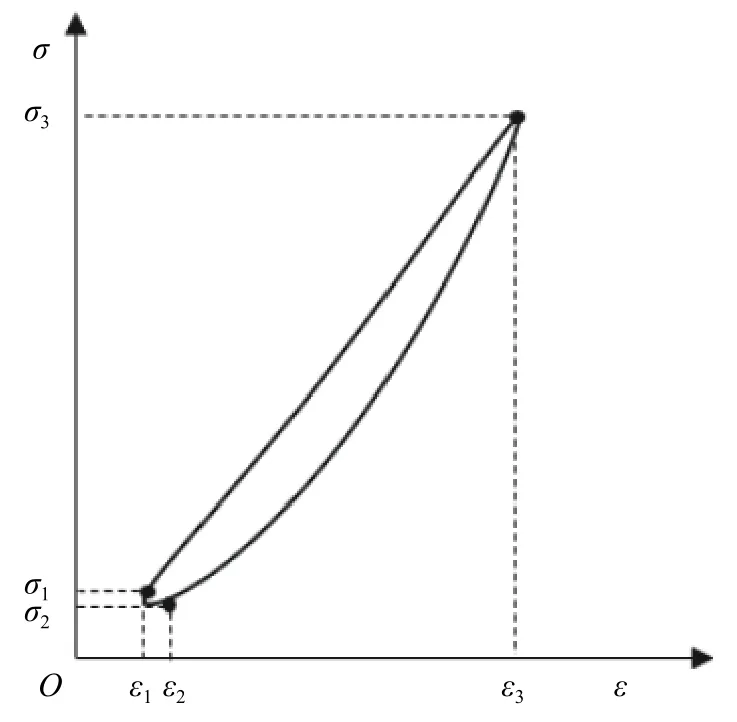
圖7 巖樣滯回環示意圖

前文已經提出，滯回環呈現為上窄下寬的尖葉形，其中下端不是嚴格的尖點，由此可以把動彈性模量公式改寫為式（4）：

σ3——試驗數據中最大應力值；

σ2——最小應力值；

σ1——最小應變對應的應力值；

ε3——試驗數據中最大應變值；

ε2——最小應力對應的應變值；

ε1——最小應變值。

由此可以利用公式（3）與公式（4）,選取第 10、300、600、900、1 200、1 500 周次滯回環數據得出圖8。

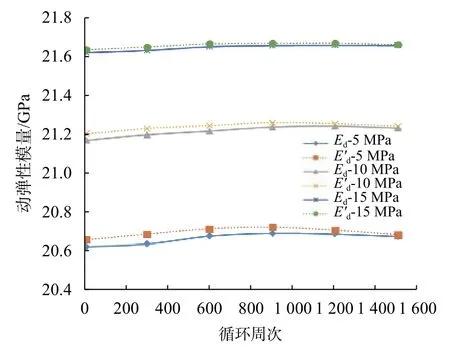
圖8 各圍壓下動彈性模量曲線

兩條曲線總體都呈上升趨勢且整體趨勢接近，大約在600次循環周期內曲線上升幅度明顯而后趨于平緩，且圍壓越大，動彈性模量越大。可以發現公式（4）比公式（3）的計算結果接近，表明修改公式具有一定的合理性；隨著圍壓的增加，兩條曲線的呈現出逐漸重合的趨勢，這可能是圍壓將巖樣內部的空隙壓密甚至使其閉合，巖樣內部變得更加具有連續性與傳遞性，在某一范圍的荷載條件下，由于同屬一種板巖，動彈性模量隨著圍壓的增加會逐漸靠攏一個定值，這也可以側面說明圍壓減小了滯后性。

4 結束語

巖樣在加載階段的應變相位超前于應力相位，分析其主要原因可能是在由卸載轉變為加載時，剛性墊塊與巖樣之間發生撞擊產生了反彈力，巖樣在受到反彈力與荷載的共同作用下發生變形，造成加載階段應變相位略領先于與應力相位。

基于試驗數據以及分析，認為滯回環形狀呈上窄下寬的尖葉形，其中下端不為嚴格的尖點。由此提出了動彈性模量的修改公式，并比較了傳統方式和修改后計算方法，得出修改公式計算結果與傳統公式的結果相近，表明修改公式具有一定的合理性。

圍壓的增加會使兩種計算公式得出的曲線逐漸重合，使兩種公式的計算結果更接近，由修改公式是根據巖樣的滯后現象提出，結合圍壓在增大的過程中應力應變相位差逐漸減小，表明圍壓會對巖樣的滯后性產生影響，且圍壓越大，滯后現象越不明顯。