基于云模型-LSTM的光伏功率中期預測

張晉華 ，2，黃遠為 *，馮 源

（1.華北水利水電大學電力學院，河南 鄭州 450045；2.新能源電力系統國家重點實驗室（華北電力大學），可再生能源學院，華北電力大學，北京 102206）

0 引言

近年來，全球范圍大力發展太陽能、風能等清潔能源。截至2020年底我國光伏發電累計裝機達2.53億千瓦，如何最大程度保證光伏發電能夠安全、高效地消納成為一大難題［1-3］。光伏發電具有隨機性、不確定性的特點，精準的功率預測能夠指導電網調度部門合理安排，減少光伏電站接入對電網的沖擊和棄光現象的發生［4-5］。光伏功率預測按時間尺度可分為超短期預測，短期預測以及中長期預測［6］。當前我國新能源功率預測3 d的時間尺度不能與火電的啟停5-7 d的周期相匹配，調度部門不能將新能源納入開機計劃進行有效指導［7］。因此，對光伏功率進行周期為7 d的中期預測具有現實積極意義。

傳統的光伏功率預測方法有物理方法和統計方法［8］。物理方法是參照光伏電池的發電原理，利用數值天氣預報（Numerical Weather Prediction，NWP），衛星、地面場站實時數據，結合光伏電池安裝角度、光伏陣列轉換效率等參數，建立物理模型直接計算得到光伏功率數據［9］。物理方法對數據精度要求高，且模型參數多，構建難度大。統計學方法是輸入太陽輻照度、光伏功率等歷史數據，通過曲線擬合、參數估計等方法，建立輸入與輸出的映射模型從而實現預測。相比物理方法，統計方法因其模型搭建簡單，所需數據容易獲取而被廣泛應用于光伏功率預測中。常用的統計學方法有：灰色模型［10-11］、人工神經網絡［12-13］、支持向量機［14-15］等。然而傳統算法面臨著泛化能力不足和易陷入局部最優問題，預測精度難以提高［16］。

LSTM神經網絡作為一種深度學習算法，能夠準確描述此類復雜非線性映射關系，近來不少學者將其應用于光伏［17-18］、風電［19-20］及負荷預測［21］等領域。文獻［22］基于多維氣象因素間的加權互信息熵從歷史日中篩選出預測日的相似日樣本，利用LSTM預測模型建立起氣象因素與光伏輸出功率之間的映射關系，在多種氣象條件下進行了預測分析，得到了良好的預測精度。文獻［23］在選取周邊電站考慮其空間相關性的基礎上，利用相關性強的參考光伏序列同目標電站歷史光伏數據一起構建LSTM預測日模型，相較于未考慮空間相似性分析的預測模型，精度得到了提升。選擇文獻［24］引入了Davies-Bouldin指數得到自適應Kmeans算法，利用該算法分別對晴天、多云以及雨天這三類氣象條件下的總輻照度、濕度、溫度以及光伏功率進行聚類分析，最后將每一類的訓練集代入LSTM預測模型，得到預測結果。以上LSTM神經網絡在光伏功率預測中的研究集中在短期預測，尚未應用于時間尺度更長的中期預測中。

基于以上分析，本文提出了一種基于云模型-LSTM的光伏功率中期預測方法。方法首先以輻照度為樣本建立每日輻照度云模型，通過云變換得到云的數字特征，將數字特征代入云模型的相似度計算模型，選取相似日。最后將相似日數據作為訓練集代入LSTM預測模型進行預測，得到光伏功率。

1 基于輻照度云模型的相似日選擇

1.1 云模型的概念

云模型是由李德毅院士在上世紀90年代中期提出的用來描述定性概念與其定量表示之間的不確定性轉換模型［25］，設U是一個定量的論域，U上對應的定性概念為C，對于該論域的任意元素x，都由一個具備固定傾向的隨機數y=μC（x），該隨機數稱作x對概念C的確定度，x在該論域上的分布稱為云模型。云模型用期望、熵、超熵三個數值特征來描述一個概念［26］。

1）期望Ex

Ex是云滴在空間分布中的數學期望，即最能夠代表定性概念的點。在輻照度云模型中，期望值代表當日所選時段平均輻照度的大小。

2）熵En

熵值是定性概念的不確定性度量，由概念的隨機性、模糊性一同決定。熵值描述了輻照度的隨機概率分布情況，熵越大，說明當天輻照度波動越不具備規律性。

3）超熵He

超熵是熵的熵，是熵的不確定性度量。

云模型由正向云變換和逆向云變換實現定性概念與其定量表示之間的不確定性相互轉換，它把模糊性與隨機性集成到一起，構成定性與定量之間的映射［27］。根據文獻［26］提出的方法構建輻照度云模型。

1.1.1 正向云變換

輸入：當天輻照度的三個數字特征Ex，En，He；輻照度云滴數n；

輸出：n個輻照度云滴xi以及每個云滴的確定度yi，i=1，2…，n。

步驟1：生成以En為期望，He2為方差的一個隨機輻照度Eni；

步驟2：生成以Ex為期望，Eni為方差的一個輻照度云滴xi；

步驟3：計算yi=exp（-（xi-Ex）2/（Eni）2），為輻照度xi出現的概率；

步驟4：重復步驟1到3，直至產生n個輻照度云滴為止。

1.1.2 逆向云變換

輸入：輻照度x1，x2，…，xn，xi為單點時刻輻照度值，n為輻照度點數量。

輸出：輻照度的數字特征（Ex，En，He）。

步驟1：計算當日輻照度的均值，得到期望Ex的估值；

步驟2：將每日輻照度樣本x1，x2，…，xn進行隨機可重復抽樣，共抽取m組樣本，每組r個樣本點。計算每組樣本方差：

步驟3：從樣本y12，y22，…ym2中計算En2，He2的估值。

圖1、圖2分別為正向云發生器和逆向云發生器的示意圖。

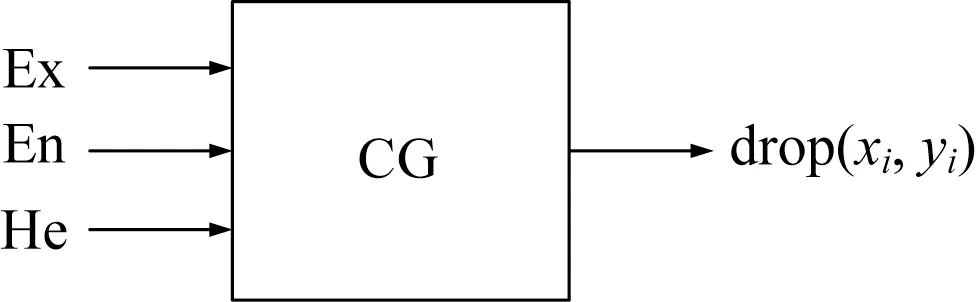
圖1 正向云發生器Fig.1 Positive cloud generator

圖2 逆向云發生器Fig.2 Reverse cloud generator

1.2 云模型3En規則

模型的3En規則即在［Ex-3En，Ex+3En］區間內分布著99.74%的云滴，由于區間外的云滴數不影響整體特性，故可忽略區間外定量值對定性概念的貢獻［28］。

1.3 輻照度云模型的相似性度量

由文獻［27］指出的方法計算云C1（Ex1，En1，He1）和云C2（Ex2，En2，He2）的交點f1和f2。

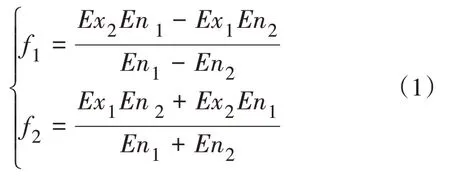
根據交點f1和f2位置關系的不同，在計算輻照度云模型相似度時，可分為以下3類情形。

情形1：交點f1和f2全位于3En區間外。這類情況下的云模型相似度為：

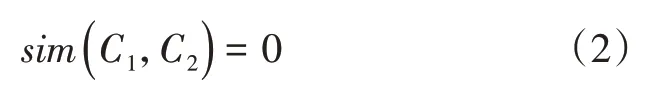
情形2：交點f1和f2有一個位于3En區間內。先求出此時C1與C2的重疊度ol［27］，這種情況下云模型的相似度為：

式（3）中，μ為兩條期望曲線交點對應的縱坐標，即確定度值。

情形3：交點f1和f2均位于3En區間內。此時云模型的相似度為：

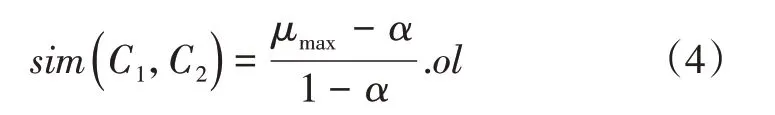
式（4）中，μmax為交點f1和f2對應的兩個確定度中，數值更大的一個。

云模型相似性度量具體算法如下：

輸入：兩個云C1（Ex1，En1，He1）、C2（Ex2，En2，He2）。

輸出：云模型相似度值Sim（C1，C2）。

步驟1：先求出兩個云的交點f1和f2；

步驟2：計算輻照度云模型的相似度Sim（C1，C2）；

步驟3：重復步驟1、2直至計算完所有天數同預測日輻照度云模型的相似度；

步驟4：對相似度進行排列選取相似度最高的3天作為預測模型的訓練樣本。

2 LSTM神經網絡

LSTM神經網絡由Hochreiter與Schmidhuber在1997年提出，旨在改進RNN的缺陷［29］。LSTM神經網絡在RNN的基礎上引入了細胞狀態，并使用輸入門、遺忘門、輸出門3種門來保持和控制信息，可對較長時序信息選擇性地通過和剔除。LSTM改善了傳統RNN網絡在長時間序列學習過程中易出現的梯度消失和梯度爆炸現象［30］。圖3為LSTM神經網絡的結構圖。

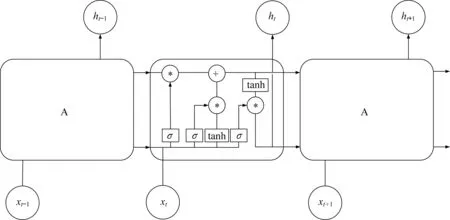
圖3 LSTM神經網絡結構圖Fig.3 Structure of LSTM neural network

LSTM模塊當前輸入時刻為t，存儲單元由以下構成。

輸入門：記憶一部分遺忘門輸出的信息和當前的信息；

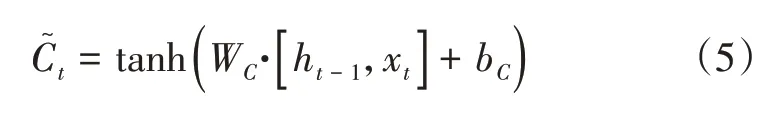
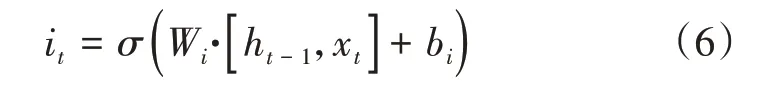
遺忘門：讀取上一層輸出ht-1以及當前輸出xt，輸出ft并將其賦值到當前的細胞狀態Ct-1中；

更新門：將過去的細胞狀態Ct-1和當前的細胞狀態C?合并，輸出得到當前的信息Ct；

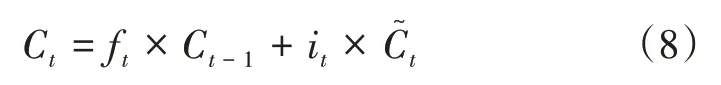
輸出門：選擇部分細胞狀態C?，輸出。

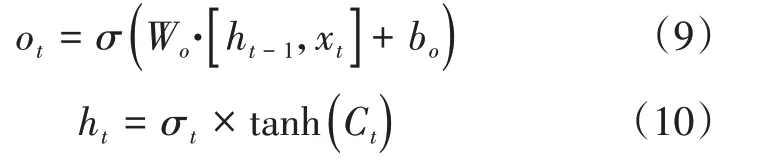
3 預測步驟

3.1 輻照度云模型的相似性度量

將每天原始輻照度樣本進行隨機可重復抽樣，抽取m組樣本，且每組抽r個樣本點，抽樣結果代表當天輻照度的情況。將這m組輻照度樣本代入逆向云模型進行計算，得到m組（Ex，En，He）數字特征，最后對m組數字特征取平均值作為當日輻照度逆向云計算結果。經多次驗證，m和r分別設置為20和25進行隨機抽樣較為合理。

3.2 LSTM預測模型設置與預測

3.2.1 輸入層與輸出層節點數目

選取輻照度、溫度和濕度數據作為LSTM預測模型的輸入，光伏功率作為神經網絡的輸出。在構建LSTM光伏功率預測模型時，將歷史日的以上氣象因素與光伏輸出功率一一對應，作為訓練集。將預測日的輻照度、溫度、濕度作為測試集輸入，得到預測日的光伏輸出功率。由此確定光伏功率中期預測模型的輸入層和輸出層節點個數分別為693和231。

3.2.2 隱含層節點選擇

隱含層單元數目為用于記憶和儲存過去狀態的節點個數。若設定數目過少，則LSTM網絡無法全面學習，誤差較大。若隱含層單元數目過多，則LSTM網絡學習速度慢，且易發生過擬合現象。根據經驗公式取得估值，反復多次實驗，確定LSTM隱含層節點j。經驗公式如下：

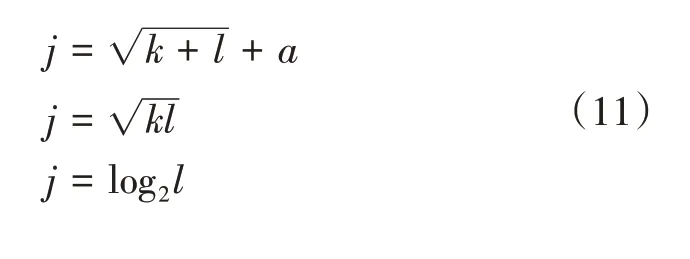
式（11）中：j為隱含層個數；k為輸入層個數；l為輸出層個數；a為1到10中任一常數。

由表1可以看出，當隱含層數目為30時模型的均方根誤差最小，由此將模型的隱含層節點數設置為30。

表1 隱含層節點個數確定Table 1 Determination of number of hidden layer nodes

3.2.3 數據標準化與標準化還原

由于激活函數的特性，使得神經網絡對區間［-1，1］內的數據敏感。若輸入數據在此區間，則會大大提升訓練速度，獲得較好的擬合曲線，避免訓練發散。因此，首先將訓練數據標準化，使其具有零均值和單位方差。最后將輸出的數據進行標準化還原，得到預測的光伏輸出功率。

3.3 評價指標

本文衡量預測效果的指標采用平均絕對誤差百分數（MAPE）以及均方根誤差（RMSE）。計算公式如下：

式（12）、式（13）中，Pi為第i個預測功率數據的真實值；Pi'預測值；Pcap為該光伏電站的裝機容量；n是樣本個數。

4 算例分析

采用國內某光伏電站現場實測數據進行預測。該電站裝機容量為50 MW，實測數據包含輻照度、濕度、溫度、風速、風向及光伏發電功率。為了驗證所提預測方法的有效性，考慮季節差異，選取每日時段為9：00到17：00，采樣間隔15 min，一天采樣33個點。本文考慮了電站春夏秋冬4個季節，在實驗中引入長短期記憶網絡（LSTM）、灰色模型（GM）、支持向量機（SVM）等預測模型進行光伏功率預測，最后與本文提出的云模型-LSTM模型預測結果對比，如圖4所示。

由圖4（a）可以看出，除了前兩日的功率曲線有些許波動外，七日內整體功率曲線的隨機波動頻率較低，且波動幅度較小。各模型的預測曲線與真實值擬合程度都比較高。相比于圖4（a）冬季，圖4的（b）、（c）、（d）春夏秋3個季節的功率曲線波動頻率更高，波動幅度也相對更大。預測效果不及冬季7日預測，原因是電站所處地區冬季空氣中水汽含量低，云層少。云層作為主要的天氣突變因素，直接影響地表輻照度水平。當光伏功率曲線波動頻率高，波動幅度大時各模型的預測精度也隨之下降。但對比其他模型的預測曲線可以看出，本文所提云模型-LSTM的預測曲線更接近真實值，反映了云模型-LSTM具有較強的學習能力。

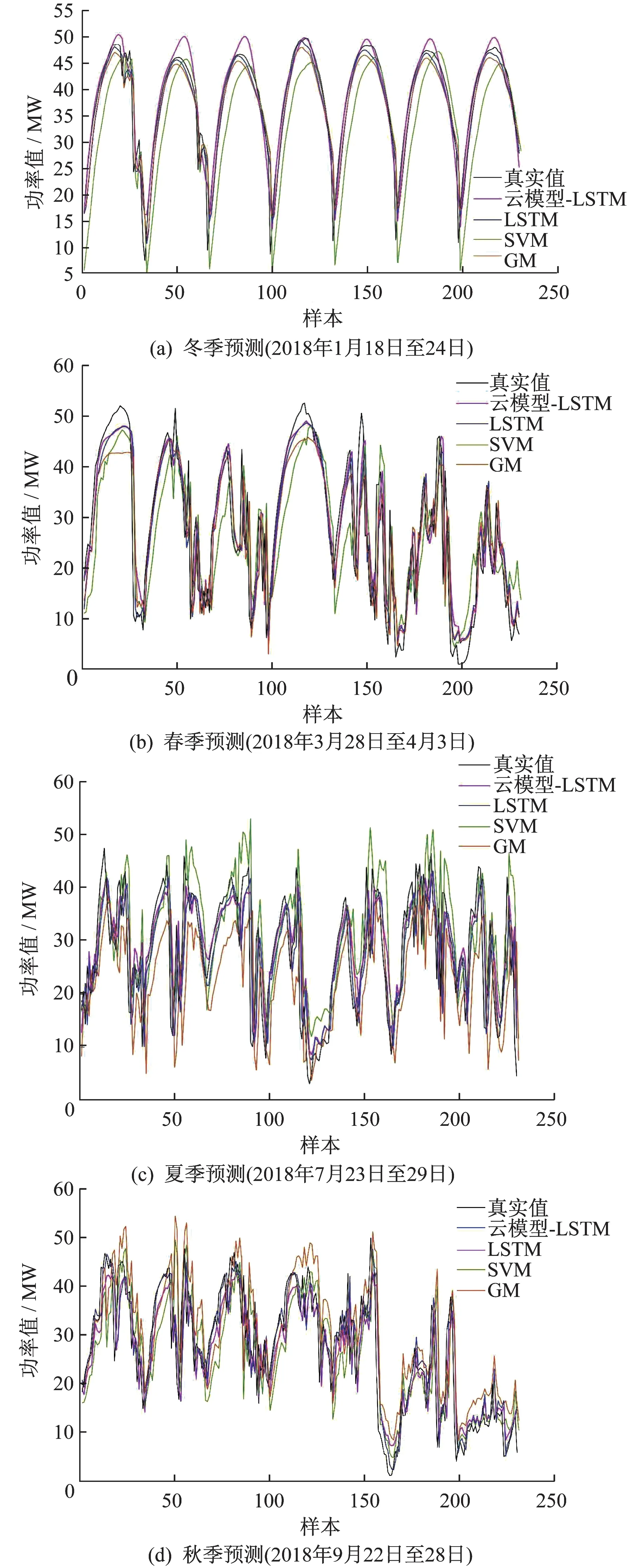
圖4 預測結果Fig.4 Forecast

表2為在春夏秋冬四個季節的不同預測模型進行光伏功率預測的誤差對比。由表2可以看出，在冬季時各模型的預測效果均比其他季節的要好，且本文提出的云模型-LSTM預測光伏功率中期模型預測誤差更小。上述結果表明，云模型-LSTM具有更好的預測精度，在不同季節均可以更好地對光伏功率進行預測。相比于LSTM預測模型，云模型-LSTM在冬春夏秋四個季節下的MAPE分別降低了40.10%、8.40%、5.75%和19.56%，RMSE分別降低了46.43%、2.20%、2.24%以及3.42%。這表明結合了云模型的LSTM模型在預測精度上有進一步的提升。特別地，冬季光伏功率預誤差明顯降低，這反應在冬季季節氣候時云模型能夠篩選出與待預測日高度一致的歷史日，而對于其他季節，在天氣相對復雜時，云模型的這一表現有所降低；LSTM預測模型相較于SVM和GM，在冬季MAPE分別降低了10.66%、9.74%，RMSE分別降低了9.98%、9.37%；在春季MAPE分別降低了10.08%、11.50%，RMSE分別降低了3.93%、4.50%；在夏季MAPE分別降低了3.74%、4.16%，RMSE分別降低了1.73%、16.33%、；在秋季MAPE分別降低了7.13%、18.89%，RMSE分別降低了5.25%、2.54%。這也表明了相對于傳統統計學算法，LSTM具備泛化能力強，預測精度高的特點。

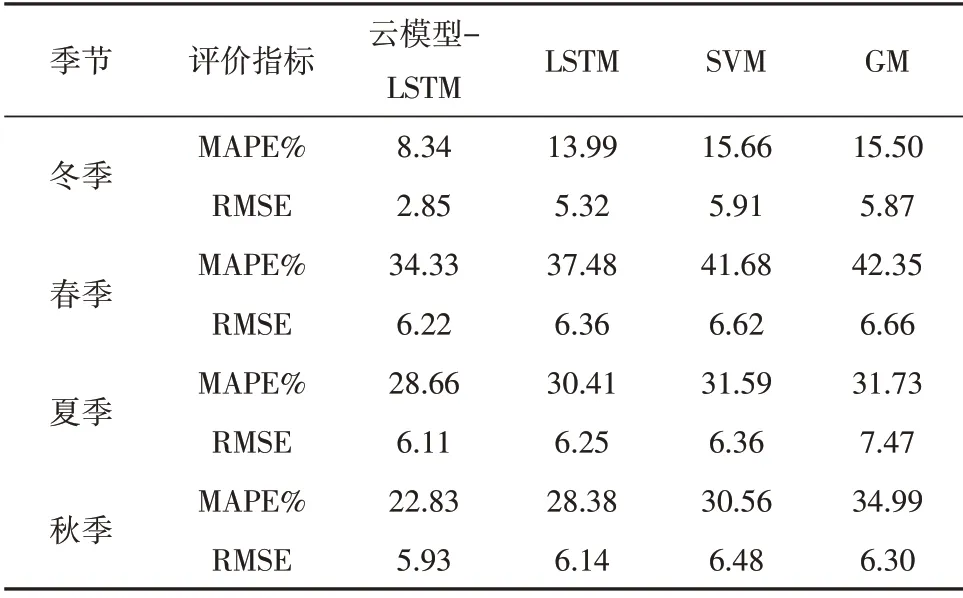
表2 預測誤差統計表Table 2 Statistical table of forecast error

5 結語

本文提出了一種基于輻照度云模型與LSTM的光伏功率中期預測方法，首先提取每日輻照度形成訓練集，然后利用云模型的相似性度量計算選取相似日，最后利用LSTM神經網絡對光伏功率進行預測。為了驗證預測的性能，本文以國內某光伏電站實測數據為研究對象與傳統LSTM、SVM以及GM模型進行對比實驗，結果表明，本模型在不同季節、不同氣象條件下均能夠提升光伏功率中期預測的精度，具有一定的研究價值和應用前景。

本模型的主要不足之處在于對復雜氣象條件下的預測精度未有明顯提升。此外，當前建立的云模型在進行相似日選取時僅考慮了輻照度，在未來的研究中可以考慮納入更多諸如溫度、濕度等其它影響因素，篩選出與待預測日氣象條件更加相近的歷史日。