基于智能電網的電動汽車充放電分時電價及引導策略
蔣俊峰,譚倫農,紀棋彬
(江蘇大學 電氣信息工程學院,鎮江 212013)
隨著全球經濟持續發展,為緩解能源危機和環境污染問題,世界能源加快轉型。目前,發電環節是能源消耗與碳排放最大的來源之一。因此,各國政府和企業通過采取轉變發電方式等措施來降低碳排放。其中新能源發電前景廣闊,以風能、光能為代表的清潔能源逐漸成為可持續發展的重要標志之一。根據相關權威機構預測,到2050年,世界范圍內清潔能源占總能源的比例將過半。在將來的電力系統中,常規能源逐步被淘汰,高比例可再生能源成為時代的主流。高比例可再生能源發電接入電網將導致供求曲線的不穩定。與傳統的汽油車和柴油車相比,具有綠色、環保、高效等優點的電動汽車逐漸成為市場上的寵兒,大有代替常規汽車的趨勢。大規模電動汽車無序接入電網也將導致供求曲線不穩定。
然而,電動汽車的優勢是可作為移動的儲能裝置經有序充放電能完美地消納風能、太陽能等可再生能源,實現供求曲線的穩定。為引導電動汽車有序充放電來消納新能源,實現供求曲線平衡,采用分時電價機制引導電動汽車用戶有序充電。消費者在政府優惠政策和電力營銷策略刺激下轉向消費電動汽車。電動汽車充電站設置分時電價進一步引導消費者消費,并使消費者形成良好的充放電習慣。云存儲技術和智能電網相輔相成。云存儲技術包含分布式存儲和計算功能,能實時收集信息、傳輸信息,響應用戶的需求。
國內對于電動汽車充放電價格的研究雖有不少,但大都還處在理論階段,尤其是結合可再生能源的相關研究更為匱乏。國外對電動汽車充放電價格的研究更為多樣化,且已將相關理論運用于實踐,并取得了不錯的效果。國內學者可結合國情以此為鑒,充分吸收并探索出更有意義的成果。文獻[4]中雖然考慮了需求響應,并以此為依據制定了動態價格,但是未進一步考慮可再生能源的應用,研究供給側的變化。文獻[5]中為了滿足電動汽車充電站的需求,考慮了價格信息和用戶的充電習慣,擬定了充電價格策略,但并未考慮到放電價格的制定及引導策略,沒有充分發揮電動汽車充放電的潛能。文獻[6]在文獻[5]的基礎上進一步加入了V2G(vehicle?to?grid)模式,并考慮了配電側風光互動,協調控制其運行,但在價格引導方面還尚有欠缺。在文獻[7–11]中利用多種價格機制來控制一天中電動汽車在日常居住地的充電模式。然而,在商業或者工作地帶,用戶并不能對電動汽車的充電進行實時控制,需要設定一定的充電量和充電期限。文獻[12–13]中提出了基于需求側響應的價格優化算法,然而在實際情況下,需實時響應用戶的充放電請求。文獻[14]中提出了一種在線VCG(Virkrey?Clarke?Groves)模式,然而用戶需支付的費用是在充電后才能確定,所以用戶在充電前并不知道充電價格,因此該模式并不能起到很好的價格引導作用。文獻[15–18]中提出了多種電動汽車在線有序充電算法。這些文獻主要致力于有序引導策略的研究,并未考慮到為充電站和用戶提供價格優化。
本文應用云存儲技術,實時響應用戶的充放電請求,提高客戶的滿意度。在目前已有的研究基礎上,考慮到高比例可再生能源和電動汽車接入電網帶來的問題,充分發揮電動汽車的存儲功能,并有效利用充電站設施,提出新型價格模型。通過對電動汽車進行有序引導,縮小供求曲線的差距,保持供求曲線的穩定。對所提出的模型進行優化和數據分析,以期驗證該模型的有效性。
1 電動汽車充放電對供求曲線的影響
1.1 電動汽車能量
借助云存儲技術和智能電網,可實現智能電網和電動汽車用戶之間的信息互動。在此考慮高比例可再生能源和大規模電動汽車接入電網對源?荷端的影響。
假設在一個地區范圍內有n輛電動汽車,m個電動汽車充電站,充電站內有p個充電樁。為便于仿真模擬,假設電池種類、特性相同,且電動汽車充電站中每個充電樁均具有雙向傳輸電能的功能。
在此研究一天中電動汽車充放電價格。將一天24 h平均分成24個時間段,每個時間段Δt=1h 。 Δt可以按需求設置為更小的值。充放電電動汽車集合為
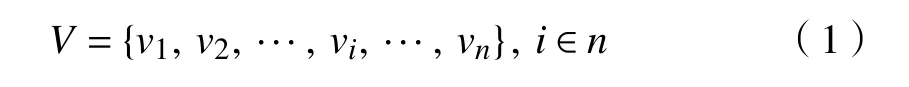
式中,v表示第i輛電動汽車。
電動汽車集合V包含兩個部分:在t時刻只參與充電的電動汽車集合V,其數量為 n;只參與放電的電動汽車集合V, 其數量為n。因此有
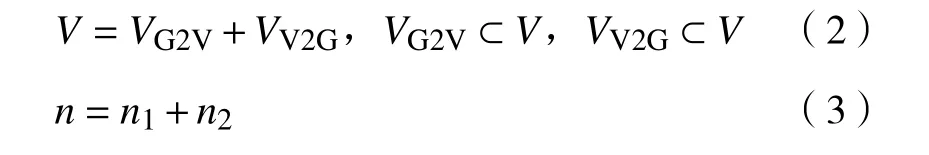
本文中考慮的是某個地區范圍內的電動汽車充放電行為。這個地區所有的電能消耗由一個智能微電網(smart microgrid,SMG)提供。SMG基本能夠滿足所有電動汽車及生產、生活所需的電能。
在周期T中,電動汽車v充 放電量為 Q,有
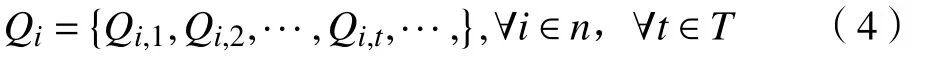
式中, Q為電動汽車 v在t時刻的交互電量。
電動汽車v在 t時刻的充電量表示為Q,其取決于t時刻的電池狀態S和 充電目標量E。放電量表示為 Q,其取決于t時刻的電池狀態S和 放電目標量 E,從而可以得到
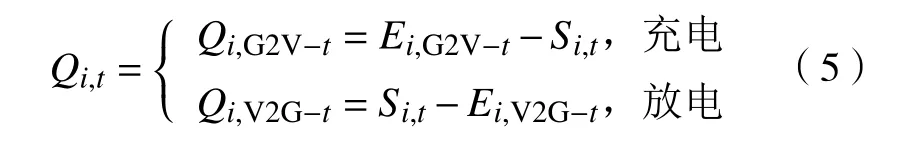
1.2 供求曲線
智能微電網采取常規能源和高比例可再生能源兩種能源發電方式。微電網在t時刻供給量為 Q,需求量為 Q。為了表征供求曲線之間的差異,分別計算兩者之間的差值 Q和比值Q,即
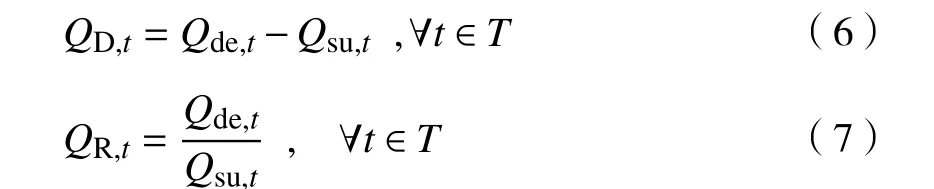
Q包括常規能源 Q、可再生能源Q和電動汽車放電量 Q的總和。另一方面,Q包括正常生產生活所需能量 Q和電動汽車充電量 Q的總和。因此有
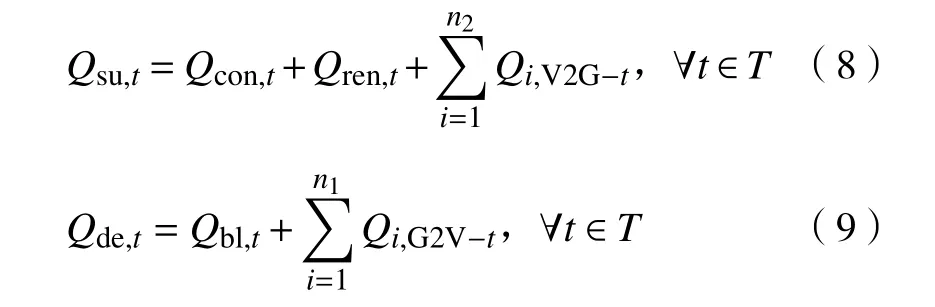
從式(6)~(9)中可得:可再生能源發電與電動汽車充放電直接影響供求曲線的穩定性,兩者對供求曲線的穩定性可產生積極或消極影響。
2 分時充放電價格的制定
2.1 價格模型
云平臺作為電動汽車和充電站之間溝通的橋梁,能夠實時獲得充電站的空閑情況并響應電動汽車的充放電請求。每輛電動汽車的相關信息V均存儲在云端。
V包含用戶姓名、用戶密碼、汽車序列號、電池類型、電池效率、電池狀態和充電速度。根據充放電效率、充電速度和電池的電量狀態等信息,可計算得到電動汽車的充放電時間。電動汽車在t時刻向云端發出充放電請求,包括充放電的時間范圍和充放電的目標范圍。然后經過云計算,將最合適的時間、價格發送給電動汽車,引導其充放電。
本文中考慮了兩種價格優化模型:充電價格C和放電價格 C。基于預測的供求曲線,可以得到
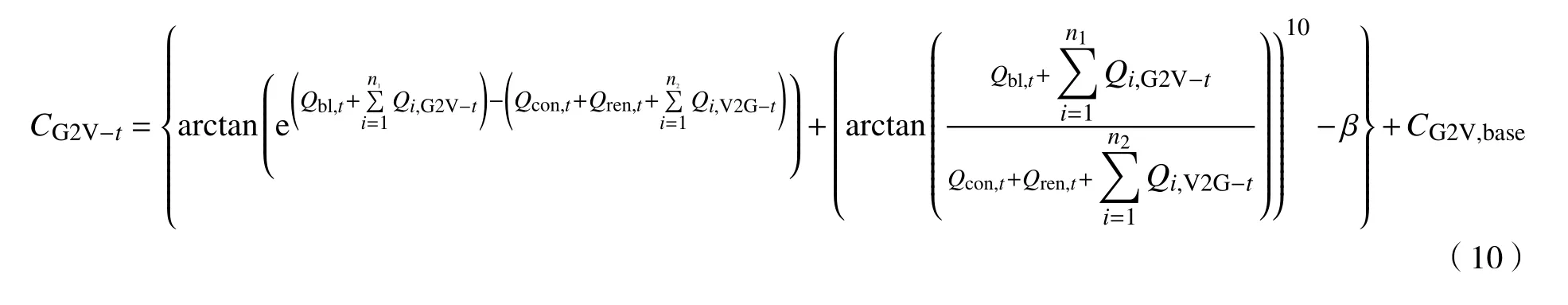
式中:C為 從電網購電的成本;β為預先給定的常數。
從式(6)~(9)中可以進一步得到
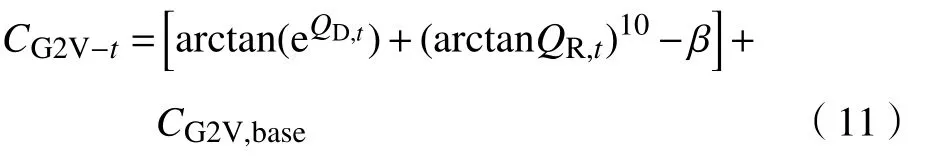
Q、 Q分別由式(6)、(7)給出。和式(10)類似,可以得到放電價格,即
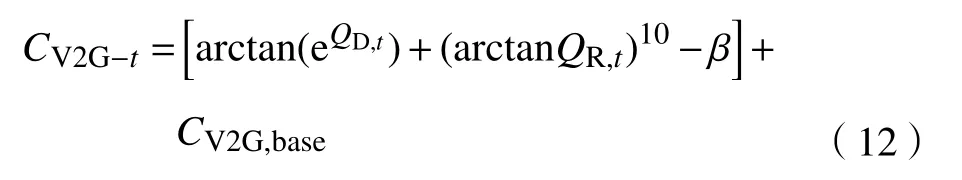
式中,C為向電網放電的基本費用。
從式(11)中可以得到:當需求量 Q不變或下降時,充電價格C隨 著供給量 Q的增加而下降。相反,當供給量 Q不變或下降時,充電價格C隨 著需求量 Q的增加而增加。
式(10)、(11)、(12)較精準地描述了電價特性,即電動汽車的充放電價格隨著供求曲線的改變而實時變化。
2.2 優化價格模型
考慮到電動汽車充放電的影響,為了控制和維持供求曲線的穩定,需積極引導電動汽車有序充放電,減小 Q和 Q之間的供求差距。充電價格下降時引導更多的電動汽車充電,放電價格上升時引導更多的電動汽車放電。為了進一步通過價格引導來緩解充電站的空閑或忙碌問題,本文中在制定電動汽車充放電價格時考慮了充電站的空閑率。加入充電站的空閑率后的價格可表示為
當供求曲線穩定( Q 式中:j表示第j個充電樁;n、 n分別為充電站內用于充電、放電的充電樁個數; C、C分別為第j個充電樁的充電價格、放電價格。 目標函數為 約束條件為 式中:Q、 Q分別為電動汽車充電能量的最小值和最大值;Q、 Q分別為電動汽車放電能量的最小值和最大值;E、 E分別為充電目標量的最小值和最大值;分別為放電目標量的最小值和最大值;C、 C分別為充電價格的最小值和最大值;S為電池的荷電狀態。 為了使模型求解簡便,假設電動汽車在快充情形下充放電,充放電功率在各個時刻保持不變。考慮到可再生能源發電的隨機性和短時間內可調度的電動汽車充放電容量的有限性,假設發電量和需求量之間的差異不會特別顯著,使得可調度電動汽車的充放電容量滿足供求穩定。 當供求曲線不穩定( Q>Q)時,有 目標函數為 約束條件為 無論是以上哪種情形,都需要解決雙目標問題,變量為電動汽車的充放電量。因此,采用線性加權法將雙目標函數轉化為單目標函數。 式中: s、 s均 為權重系數,且 s+s=1; f、f分別為 f、 f的最小值。 為了使用戶的利益和充電站的效益公平化、均衡化,在此取 s=s=0.5。在某些情況下,如果想提高某一方的利益,可適當提高其權重系數。對于線性優化模型求解,本文采用粒子群優化算法。 在此考慮兩種場景,以便進行分析、比較,以驗證所提出的模型是否能達到預期設想。第一種是常規模式,即只采用以上的定價方式,并不對其進行線性優化。第二種是采用所提出的優化價格模型。為了優化充放電價格并使供求曲線保持穩定,電動汽車用戶、充電站、智能電網需實時保持通信來響應電動汽車的充放電請求。表1、2分別為算例中采用的相關仿真參數和電動汽車參數。 表1 仿真參數 電動汽車/輛充電站數量/個充電站中充電樁數量/個充電汽車數量與充電樁數量比值/%放電汽車數量與放電樁數量比值/%充電目標量/(kW·h)放電目標量/(kW·h)2 000 20 2 000 70 30 30~60 10~30
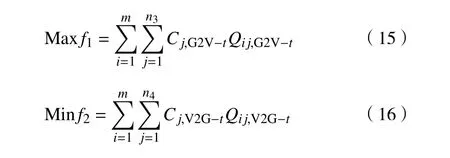
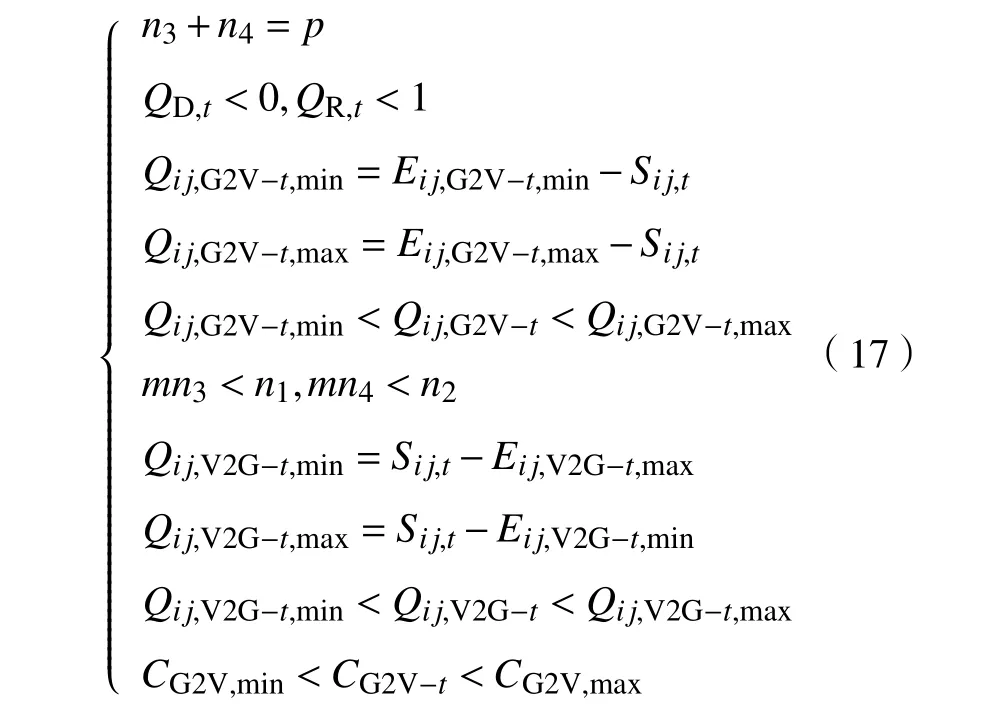
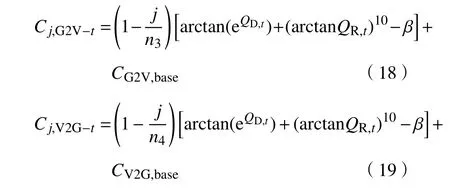
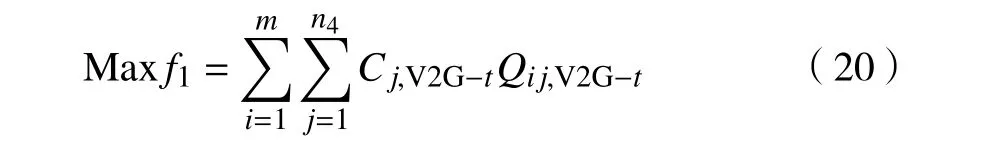
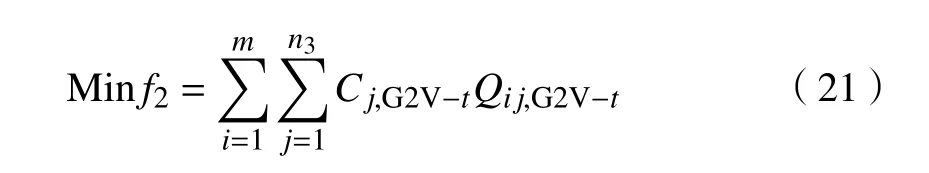
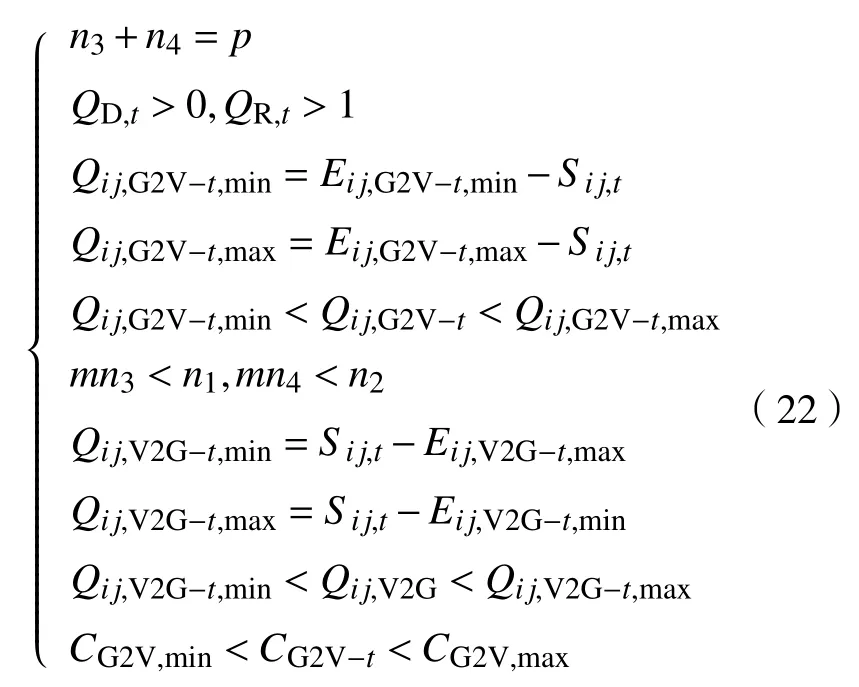
2.3 模型求解
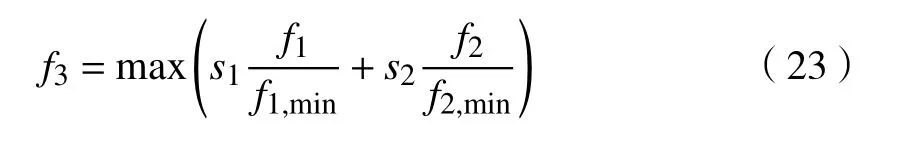
3 算例分析
3.1 參數設置
Tab.1 Simulation parameters
表2 電動汽車參數
Tab.2 Parameters of the electric vehicles (EVS)
電池儲能容量/(kW·h)額定充放電功率P/kW充放電效率/%60 9.6 90.85
3.2 仿真分析
圖1為電動汽車一天中各個時刻充放電量。從圖中可以看到,一天中有兩個高峰時期:早高峰(6:00~8:00)和晚高峰(17:00~20:00)。在高峰時期,電動汽車的數量取最大值2 000。圖2為每輛電動汽車電池初始電量。為了使仿真結果更加真實、有效,在兩種場景中均假設充電汽車數量大于放電汽車數量。
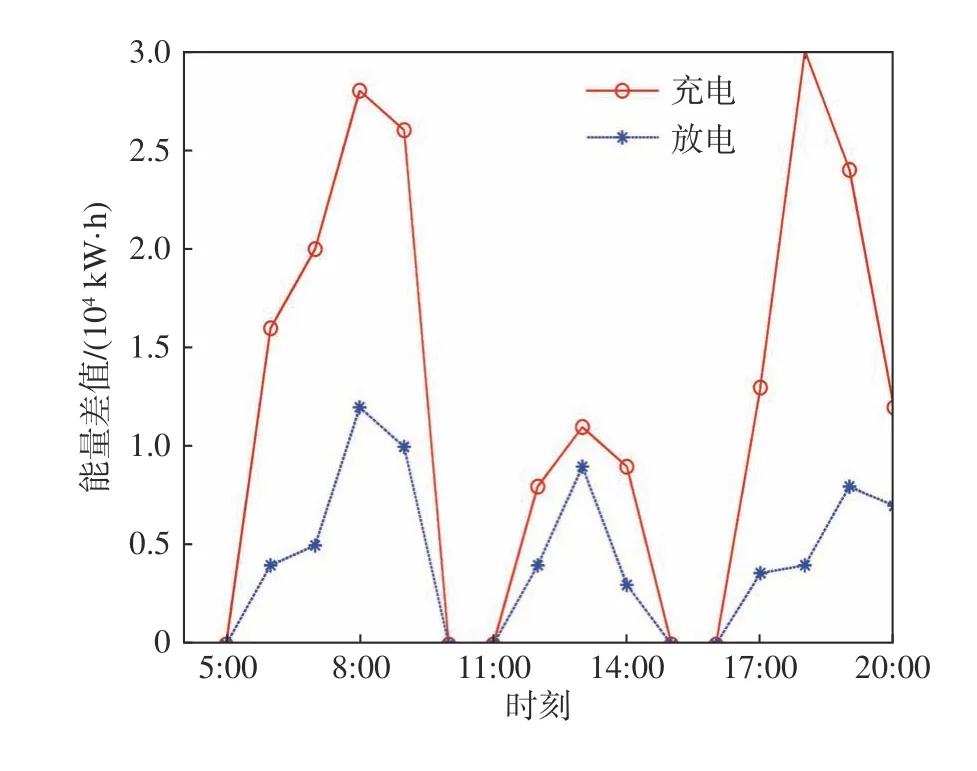
圖1 電動汽車一天中各個時刻充放電量Fig.1 Charging and discharging energy of EVS in one day
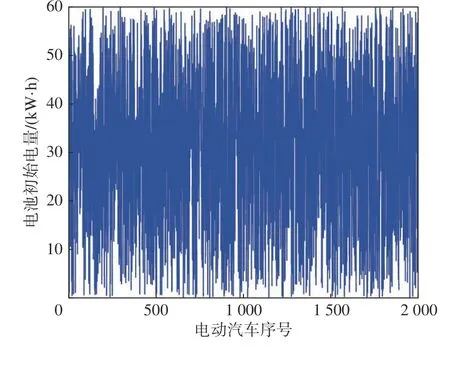
圖2 電動汽車電池初始電量Fig.2 Initial energy of EVS battery
假設供求曲線不穩定,例如供小于求,且電動汽車充放電隨機接入。圖3為常規模式下一天中充放電量差值。從圖中可以看到,在負荷高峰時期,能量供求差值顯著增加。在常規模式下某充電樁的電動汽車動態充放電價格如圖4所示。由圖中可以看出,供求曲線不穩定時,充電價格較高,尤其是在高峰時期。
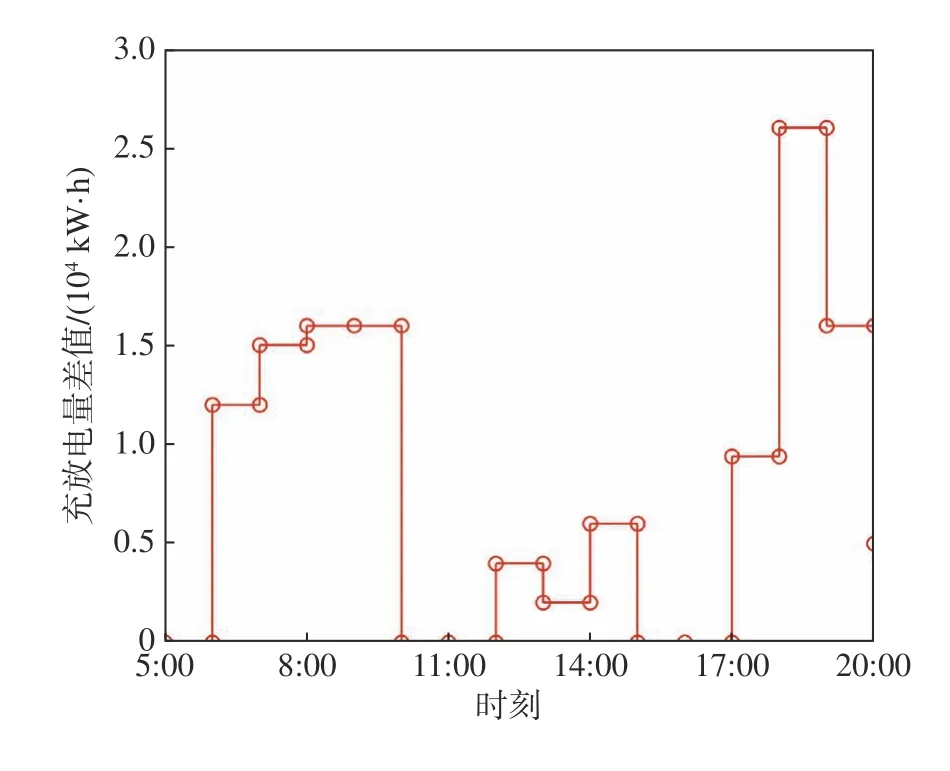
圖3 一天中電動汽車充放電量差值Fig.3 Energy difference between charging and discharging of EVS in one day
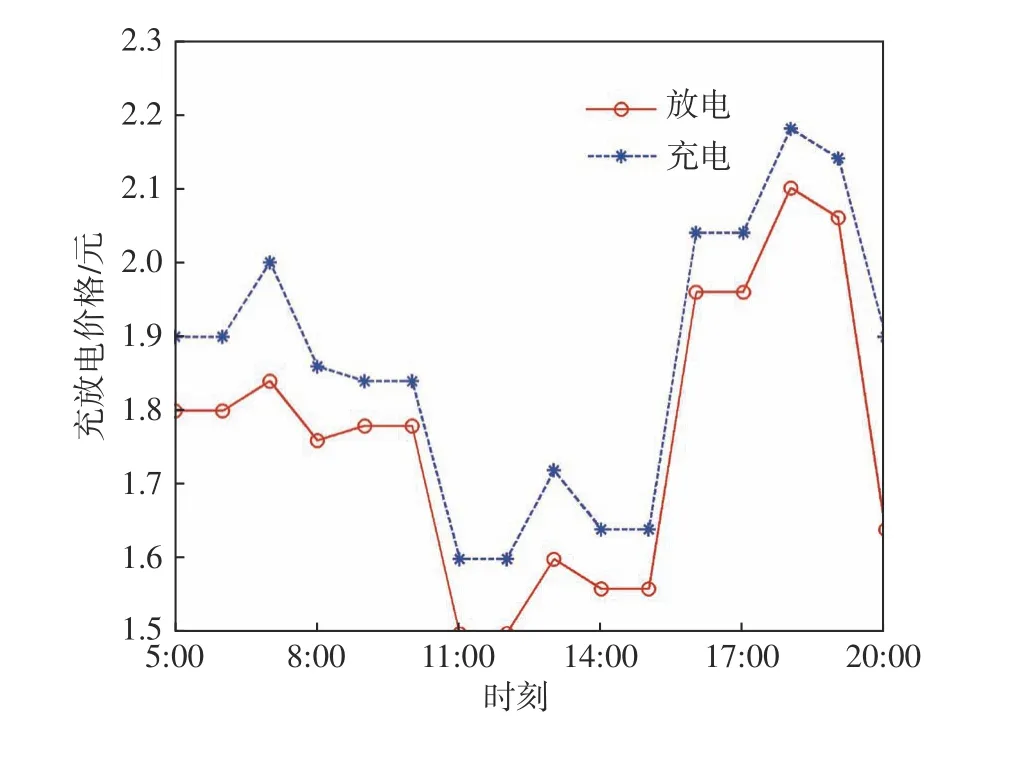
圖4 常規模式下電動汽車動態充放電價格Fig.4 Electricity price of EVS charging and discharging in the normal mode
能量比值 Q與充電價格的關系如圖5所示。當供等于求時,能量比值為1,此時電價固定。隨著能量比值的增大,電價增長。由圖5中可以看出,可用價格信息來代替供求信息。
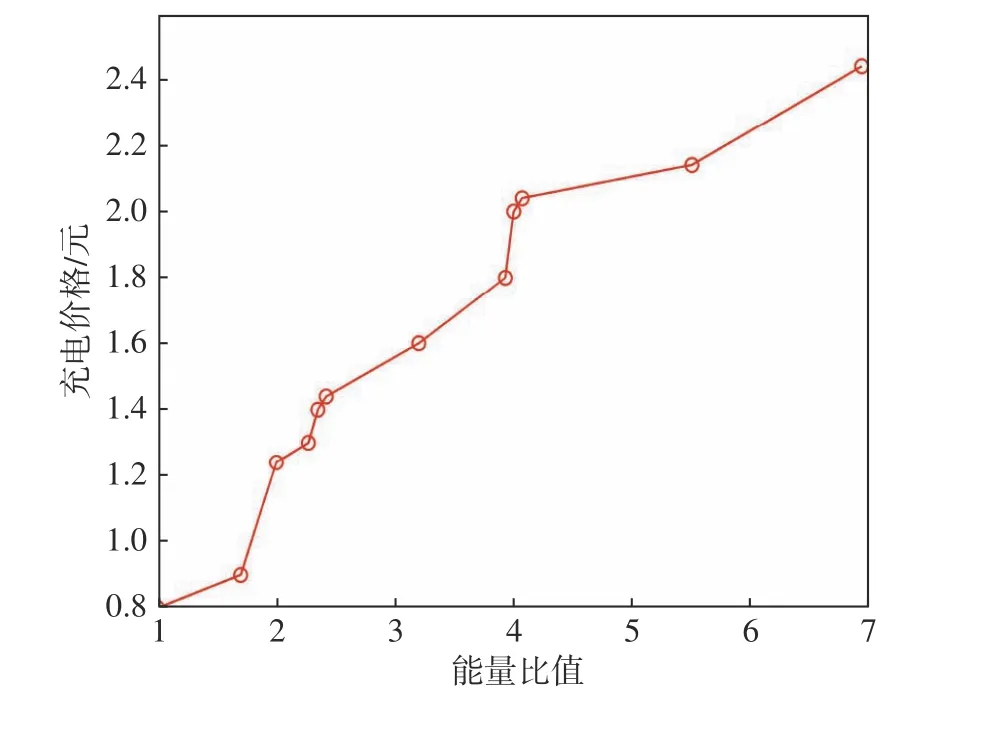
圖5 能量比值與充電價格的關系Fig.5 Relationship between the energy ratio and charging price
常規模式下和采用優化價格模型優化后電動汽車放電價格的對比如圖6所示。從圖中可以看到:早高峰時期,放電價格從1.24~1.78元上升到1.80~1.90元;晚高峰時期,放電價格從0.76~0.84元上升到1.90~2.12元。充電價格的下降在供小于求的情形下具有重要意義,表明供求曲線趨于穩定。
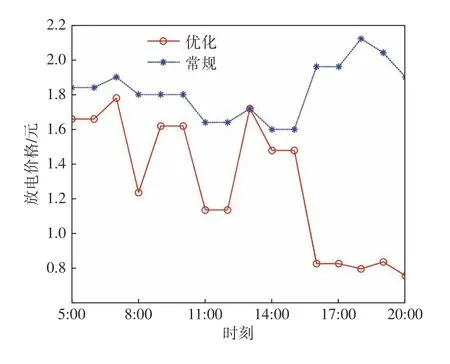
圖6 常規模式下和優化后的放電價格對比Fig.6 Comparison of discharging price between the normal mode and the optimization one
在常規模式下電動汽車無序充放電,導致供求曲線差異更大。經價格優化后充電價格下降,有序充電使供求曲線相對穩定。常規模式下和優化后的能量比值和能量差值如圖7所示。從圖7(a)中可以看到,在18:00,常規模式下能量比值達到最大值7.00,優化后下降到2.32。與常規模式下相比,圖7(b)中優化后供求能量差值的初始值為負值,此時供求關系變得穩定。從圖7中可以得出,本文所提出的優化價格模型能夠有效地穩定供求曲線。

圖7 常規模式下和優化后的供求能量比值、能量差值Fig.7 Energy ratio and energy difference based on supply and demand curve in the normal mode and after the optimization
兩種場景下電動汽車在各個時刻充電量對比如圖8所示。從圖中可以得到:與常規模式相比,優化后電動汽車的充電量有所下降,尤其是在高峰時期,8:00時充電量從14 500 kW·h下降到7 000 kW·h,18:00時充電量從15 000 kW·h下降到8 000 kW·h。對于風電功率的消納效果雖不是很明顯,但與常規模式下相比,優化后電動汽車充電站從電網購電量大大減少,減少了電動汽車充電站的運營成本。
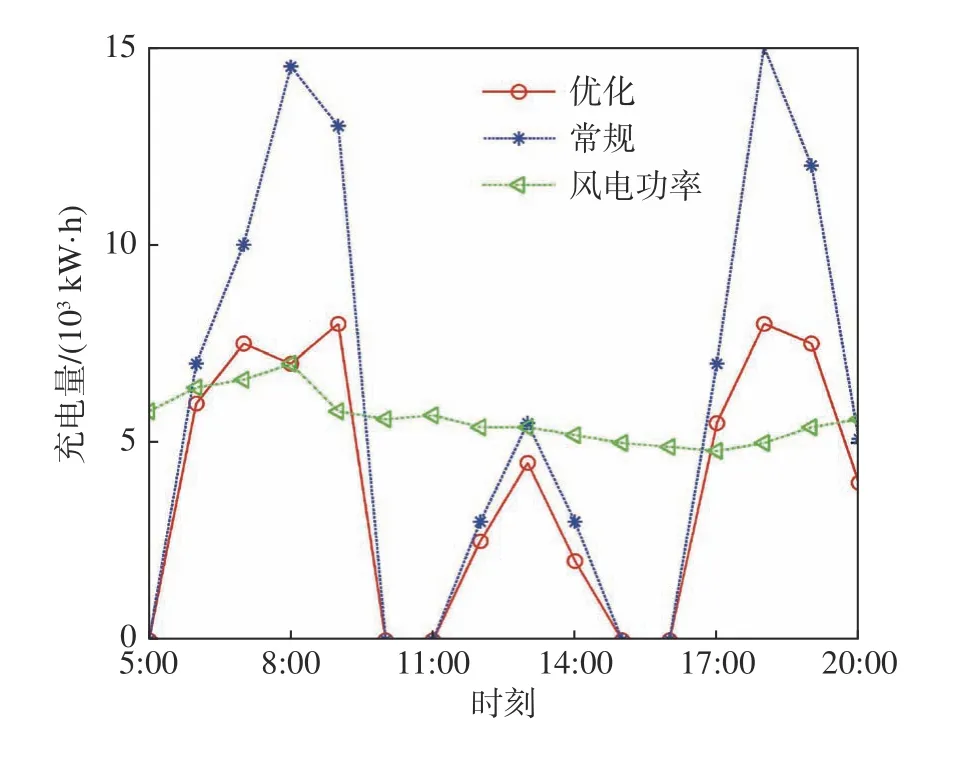
圖8 常規模式下和優化后的充電量對比Fig.8 Comparison of charging energy between the normal mode and the optimization one
常規模式下和優化后晚高峰時期供求變化如圖9所示。從圖中可以得到,與常規模式下相比,優化后供求曲線相對穩定。由此可以看出,實施優化價格模型后,供求曲線得到了較大的改善,從而驗證了該模型的有效性和合理性。
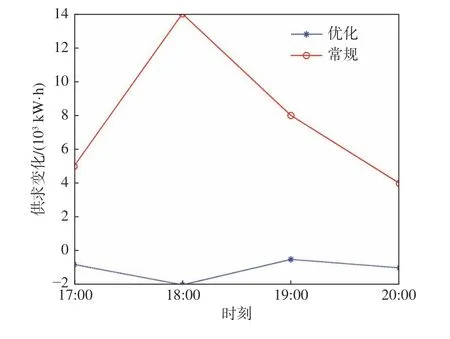
圖9 常規模式下和優化后晚高峰時期供求變化Fig.9 Supply-demand changes in the evening rush hour between the normal mode and the optimization one
4 結 論
本文提出了電動汽車的充放電價格模型,以期引導電動汽車在智能電網中有序充放電。根據供求曲線實時響應電動汽車用戶充放電請求。將電動汽車充放電價格模型歸結為多目標線性規劃問題,利用粒子群算法求解,達到維持供求曲線穩定的效果,并在高峰時期有序安排電動汽車充放電以平衡供求兩者之間的關系。當充放電價格滿足智能電網和電動汽車用戶的成本要求時,利用分時電價響應用戶充放電請求。仿真結果表明,基于智能電網技術可實現實時響應充放電需求,能有效減少供求曲線的差值,保持供求曲線的穩定性。

