地鐵車站二維抗震分析的中柱簡化方式對比

李 偉 昝子卉 趙 密

(1.北京工業(yè)大學城市與工程安全減災教育部重點實驗室,北京 100124; 2.廣州地鐵設計研究院股份有限公司,廣東 廣州 510000)

1 概述

1995年日本阪神地震，大開地鐵車站的嚴重破壞[1]引起人們對于地下結構抗震的關注和重視。近年來，科研人員圍繞地下結構抗震開展了大量研究工作[2-4]。為了簡化計算，提高效率，地鐵車站橫斷面抗震分析通常采用考慮土—結構相互作用的二維平面應變模型，中柱簡化為沿縱向連續(xù)墻體。為了降低中柱簡化處理的誤差，通過折減等效墻體的幾何尺寸或材料參數使其具有與中柱相同的截面抗彎剛度EI或抗壓剛度EA。

目前，地鐵車站的中柱等效方法有EI橫向幾何折減法[5](減小墻體橫向寬度來保證中柱截面EI不變)、EA橫向幾何折減法[6](減小墻體橫向寬度來保證中柱截面橫向EA不變)、縱向幾何折減法(將中柱平面應變單元厚度取為中柱縱向寬度，除中柱以外的土和結構平面應變單元厚度取為縱向一跨尺寸)和彈模折減法[7-9](減小墻體材料彈性模量E來保證中柱截面EA和EI不變)。李猛[10]利用EI橫向幾何折減法對地鐵車站中柱進行簡化，研究發(fā)現，地鐵車站最薄弱的位置是側墻和中柱，地震時易發(fā)生破壞。李延等[11]通過EI橫向幾何折減法將地鐵車站中柱尺寸進行折減，發(fā)現平面模型與三維實際模型最危險的位置不一致，建議如果條件允許，還是應當采用三維實際模型。周小華[12]用等代框架法對地鐵車站進行靜力計算，所得結果與實際模型的結果進行對比，研究表明，采用等代框架法對地鐵進行設計研究，在工程上是可以接受的，但是結果需要修正。張亞[6]采用EA橫向幾何折減法進行建模分析，發(fā)現利用EA橫向幾何折減法進行簡化計算時，側墻彎矩與實際有大約5%的誤差。莊海洋利用彈模折減法進行建模，發(fā)現場地類別越差，基巖輸入的地震動對層間位移角的影響越大[13]。同時，莊海洋對大開車站的破壞機理也進行了研究，利用彈模折減法進行建模，發(fā)現主體構件連接處在地震作用下容易發(fā)生損壞[14]。上述研究并未考慮中柱質量等效。本文在保證中柱質量不變前提下，討論4種中柱折減方式的適用性。

2 數值模型

2.1 地下結構參數

結構橫斷面如圖1所示。結構混凝土材料的強度等級為C35，密度為2 350 kg/m3、彈性模量為31.5 GPa、泊松比為0.2；中柱混凝土材料的強度等級為C50，密度為2 500 kg/m3、彈性模量為34.5 GPa、泊松比為0.2。結構埋深(結構頂面至地表的距離)為2.6 m，不考慮土體與結構間的接觸非線性。四個柱子的尺寸均為700 mm×1 000 mm，柱距為9 m。側墻厚度為700 mm，頂板、中板和底板厚度分別為900 mm，400 mm和1 000 mm。

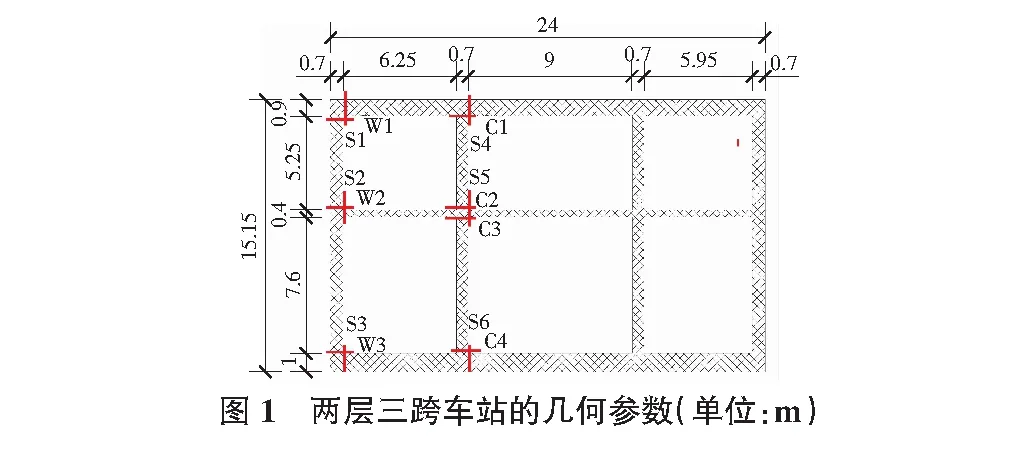
二維模型將中柱簡化為縱向連續(xù)墻體，在保證中柱質量不變前提下，通過折減墻體的幾何尺寸或材料參數使其具有與中柱相同的截面抗彎剛度EI或抗壓剛度EA，四種折減方式為：

1)EA橫向幾何折減，即減小墻體橫向寬度來保證中柱截面EA不變，墻體寬度和質量密度分別變?yōu)?.078 m和2 493 kg/m3；

2)EI橫向幾何折減，即減小墻體橫向寬度來保證中柱截面橫向EI不變，墻寬度和質量密度分別變?yōu)?.336 5 m和577.84 kg/m3；

3)縱向幾何折減，即將中柱平面應變單元厚度取為中柱縱向寬度1 m，除中柱以外的土和結構平面應變單元厚度取為縱向一跨尺寸9 m；

4)彈模折減，即減小墻體材料彈性模量E來保證中柱截面EA和EI不變，墻體的彈性模量和質量密度分別變?yōu)?.83 GPa和277.78 kg/m3。

2.2 土體參數

車站所處場地由素填土、粉質黏土、淤泥質黏土、砂黏土、強風化花崗巖組成，基巖主要是中風化花崗巖、弱風化大理巖。場地土層參數如表1所示。

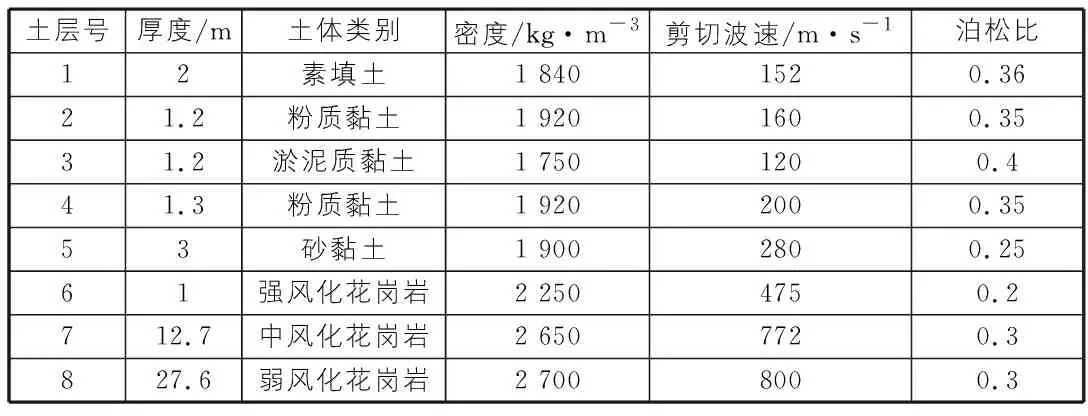
表1 場地地層土性物理參數

為考慮土體的非線性，根據杜修力等[15]的研究確定場地等效材料參數。首先利用EERA場地分析得到每層土體的等效剪切模量及阻尼比，將滯回阻尼轉化為瑞利阻尼，瑞利阻尼計算公式為：

C=αM+βK

(1)

其中，M，K分別為土體質量矩陣和剛度矩陣；α，β分別為質量系數和剛度系數。

2.3 地震動

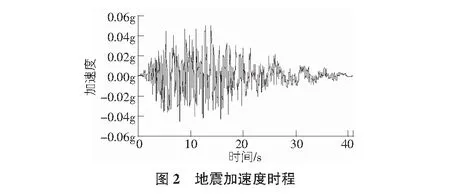
車站所處場地地震安評報告中所提供的是E2水平的場地地表地震動，故用EERA程序將場地地表地震動反演到模型底部，得到的地震動加速度時程如圖2所示，地震動總持時40.94 s,加速度峰值為0.050 6g。

2.4 邊界和初始條件

計算模型的寬度和高度分別為224 m,50 m。側邊界采用滾軸邊界模擬無限域土體的自由場效應，模型底部固定。計算過程分兩步，首先計算重力荷載作用下的初始應力場，作為下一個動力分析步的初始內力，動力計算時對整個土—結構模型施加水平向慣性力。

2.5 參考解

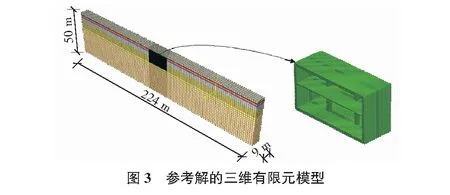
為了評價中柱簡化的精度，采用三維模型計算結果作為參考解。三維有限元模型如圖3所示，取中柱前后各半跨4.5 m，模型的兩個截斷面施加對稱邊界條件，其余材料和幾何參數均按實際選取。

3 結果討論

3.1 結構層間位移

結構的最大峰值位移出現在頂層，故給出結構頂層峰值位移及誤差結果如表2所示，從表2可以看出與三維模型的位移結果相比，EI橫向幾何折減法、彈模折減法、縱向幾何折減法的最大峰值位移誤差較小，而EA橫向幾何折減法的峰值位移誤差較大，故不推薦EA橫向幾何折減法，此后不再討論此方法。

表2 結構頂層峰值位移及誤差

3.2 構件截面的平均壓應力

構件截面的平均壓應力如圖4所示，平均壓應力誤差如表3所示。

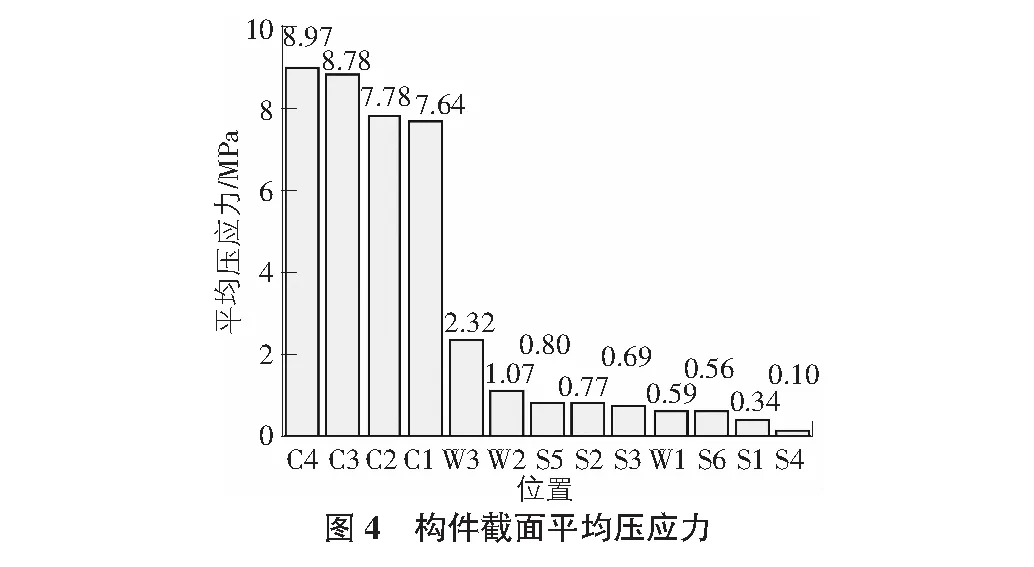
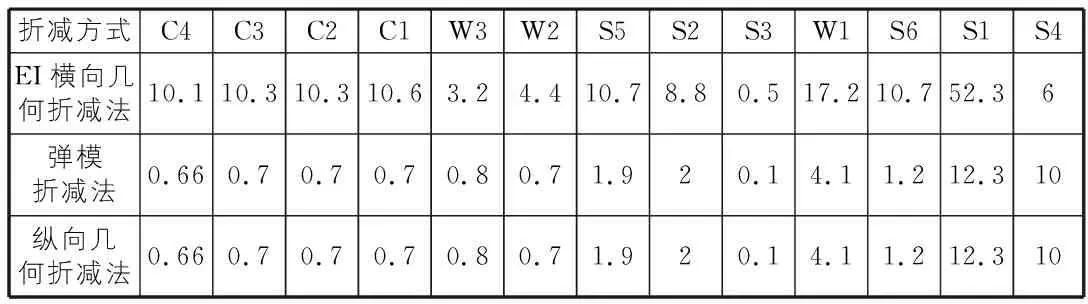
表3 平均壓應力誤差 %

3.3 構件截面的平均剪應力

構件截面的平均剪應力及其誤差見圖5，表4。

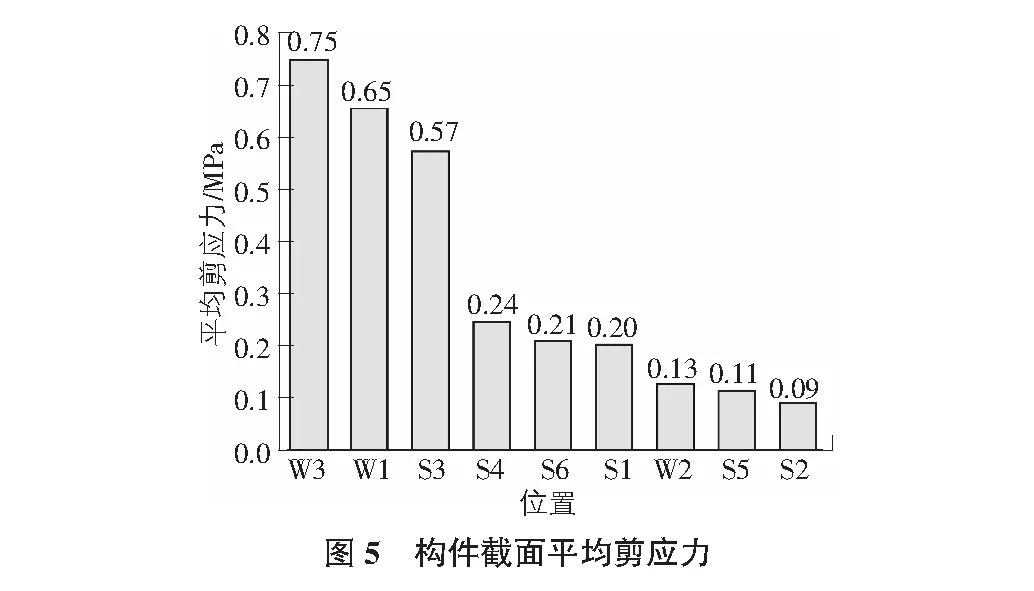
表4 平均剪應力誤差 %

3.4 構件截面的最大拉應力

構件截面的最大拉應力及其誤差見圖6，表5。

接下來討論二維模型建模方式的平均應力結果,討論截面位置見圖1。以三維模型為例，對所有截面的平均壓應力、平均剪應力和平均最大拉應力分別按照從大到小的順序進行排序，結果如圖4～圖6所示。以三維模型的平均應力為參考解，將其余二維模型的平均應力與之對比，得到所有截面的平均應力誤差，如表3～表5所示。三種截面應力分別取大小排名前三的截面誤差進行分析，彈摸折減法和縱向幾何折減法這兩種方法的誤差均小于EI橫向幾何折減法。就平均壓應力而言，前兩種方法的誤差范圍為0.66%～0.7%，EI橫向幾何折減法的誤差范圍是10.1%～10.3%。就平均剪應力而言，前兩種方法的誤差范圍為0.6%～11.9%，EI橫向幾何折減法的誤差范圍是2.4%～53.7%。就最大拉應力而言，前兩種方法的誤差范圍為0.7%～12.3%，EI橫向幾何折減法的誤差的范圍是2.7%～57.7%。

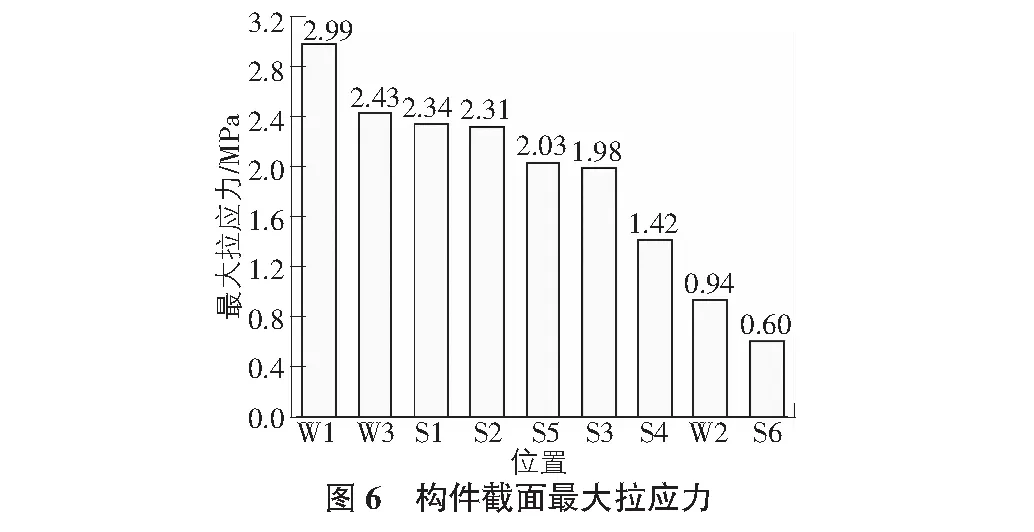
表5 最大拉應力誤差 %

4 結論

本文以某兩層三跨地鐵車站的地震響應分析為工程背景，將EI橫向幾何折減法、EA橫向幾何折減法、縱向幾何折減法和彈模折減法都考慮中柱質量等效原則對二維模型中柱材料的密度進行折減，通過與三維模型的數值結果對比，分析了以上四種處理方法的精度，得出以下結論:

1)與三維模型的位移結果相比，EI橫向幾何折減法、彈模折減法、縱向幾何折減法的最大峰值位移誤差較小，而EA橫向幾何折減法的峰值位移誤差較大，故不推薦EA橫向幾何折減法。2)研究發(fā)現，彈模折減法和縱向幾何折減法這兩種方法的平均應力誤差較小，平均應力誤差為0.6%～12.3%，因此推薦工程使用。綜上所述，在進行地鐵車站的中柱簡化時，本文推薦使用彈模折減法和縱向幾何折減法。