卷積神經網絡在地面微地震多道P波極性分類中的應用

田宵 汪明軍 張偉

1)東華理工大學，地球物理與測控技術學院，南昌 330013 2)南方科技大學，地球與空間科學系，廣東深圳 518055

0 引言

水力壓裂是頁巖氣、煤層氣等非常規油氣資源開采過程中的關鍵環節，而微地震監測技術是監測壓裂過程以及評估壓裂效果的重要手段。水力壓裂過程中巖石破裂產生的地震波信號可以被放置在井中或地表的檢波器接收，這些信號能夠用來反演震源位置、震源機制解、震級等參數，從而監測裂縫的發育過程以及評估壓裂效果(Eisner et al，2010；Maxwell，2010；宋維琪等，2013；李晗等，2018；Wang et al，2018)。地面監測和井中監測是兩種常用的監測方式。與井中監測相比，地面監測的檢波器記錄由于地震波衰減嚴重通常顯示出較低的信噪比。地面監測不僅具有較高的覆蓋次數和較寬的方位角，更易于反演震源機制解，而且具有簡單、經濟以及適應性強等優勢，因此得到了越來越廣泛的應用(Duncan et al，2010)。

微地震監測的主要內容是反演震源位置和震源機制解。震源位置能夠提供裂縫的位置和分布信息，而震源機制解可用于描述裂縫破裂類型、了解工區地應力狀態(尹陳等，2013；Zeng et al，2014；Zheng et al，2016)。大量的壓裂監測結果表明微地震事件主要是由剪切為主的裂縫破裂產生的，因此地面觀測記錄會出現P波極性變化(Eisner et al，2010；Staněk et al，2014)。P波極性信息的確定對地面微地震的震源定位和震源機制反演具有重要意義。

常用的求解震源機制的方法包括P波極性法(許忠淮等，1983)、縱橫波振幅比法(Kisslinger，1980)和波形反演方法(Li et al，2011；譚玉陽等，2019)。P波極性物理圖像明確，是穩定的地震波信息。鑒于地面監測范圍廣、微地震事件震級較小，利用不同方位的檢波器記錄的P波極性能夠反演出較為穩定的震源機制解，且求解過程具有簡單、快速等優點。因此，P波極性法被廣泛用于地面監測的震源機制反演(Staněk et al，2014；楊心超等，2015)。

地面監測數據信噪比低、數據量大，通常采用不需要拾取走時的繞射疊加定位法(Kao et al，2004；Li et al，2020)。受震源機制的影響，直接使用原始波形進行疊加會因為極性不同而導致震源位置的疊加能量降低，影響定位精度。為克服該問題，前人使用不同的波形特征進行疊加定位(Trojanowski et al，2017)，例如使用波形振幅的平方、長短時窗能量比、波形的包絡信息等；或者聯合反演震源位置和震源機制解，利用震源機制校正微地震記錄的極性(Liang et al，2016；李宏等，2018)。Trojanowski等(2017)對比了幾種常用的解決極性問題的方法，結果表明經過極性校正后的定位精度明顯高于使用原始波形以及振幅平方等波形特征的結果。因此，確定P波極性可以提高微地震繞射疊加定位的精度。

微地震監測的數據處理方法通常借鑒天然地震領域。早期的天然地震極性拾取由經驗豐富的地震工作者完成，隨著全球寬頻帶地震儀的迅速發展，地震數據量越來越龐大，這些工作逐漸被一些自動算法所替代。例如，Chen等(2016)根據拾取的P波到時，通過相位振幅和噪聲水平的比值來確定極性；Pugh等(2016)利用貝葉斯算法進行P波初動方向的定量概率估計，以得到極性是正值還是負值的概率；Kim等(2017)選取信噪比較好的參考波形，通過計算目標波形和參考波形的互相關系數來獲取相對極性。極性自動拾取算法具有穩定性和可重復性，但是大多需要預先拾取P波到時，計算速度較慢。

近年來，隨著計算機領域人工智能的發展，深度學習相關技術在計算機視覺、自然語言處理、語音識別等多個領域取得了巨大的成功(Hinton et al，2012)。機器學習算法也被廣泛地應用于地震學和地震勘探領域，包括地震信號的檢測與拾取(Zhu et al，2019；于子葉等，2018；趙明等，2019；Wang et al，2019；Zheng et al，2020)、震源定位(Zhang et al，2020)，信號去噪(王鈺清等，2019)等。卷積神經網絡(Convolutional Neural Network，簡稱CNN)是一種著名的深度學習方法，主要應用于圖像分類、目標檢測和圖像分割等問題上(Krizhevsky et al，2012)。Ross等(2018)利用CNN進行天然地震極性分類，通過大量已標定極性的數據集進行模型訓練，預測精度能夠與人工拾取相匹敵。隨后，Hara等(2019)將CNN應用到日本西部地區的地震數據極性分類中，并采用不同區域的地震數據驗證了訓練的模型具有較強的適用性。除此之外，Mousavi等(2019)采用聚類方法確定天然地震信號的極性類型，該方法不需要預先對數據進行標定。深度學習算法可以直接從訓練數據中挖掘出P波極性特征，不需要預先拾取P波到時。預測新的數據時，只需要將微震事件分割成相互獨立的窗口，然后輸入到訓練好的模型中即可迅速預測出極性類型，節省了大量的計算時間。

針對地面微地震監測的檢波器布置多采用規則觀測系統，Tian等(2020)提出了多道記錄的卷積神經網絡結構(Multi-trace based CNN，簡稱MT-CNN)，以確定地面微地震事件的P波極性。該方法不同于Ross等(2018)提出的單道記錄的CNN(Single-trace based CNN，簡稱ST-CNN)，其使用多條相鄰檢波器記錄作為訓練樣本，并輸出多道記錄的極性。MT-CNN在學習P波極性特征的基礎上，進一步學習了相鄰檢波器的極性分布規律。Tian等(2020)將MT-CNN訓練為易于實現的回歸模型，輸出一組范圍在[-1，1]之間的連續變量，然后通過設置閾值進行極性分類，當預測值大于0.3時為正極性、小于-0.3 時為負極性，其余為不確定。相較基于分類模型的ST-CNN，人工選取閾值會導致MT-CNN正(負)極性和不確定性之間的預測誤差較大。此外，回歸模型使用均方誤差作為損失函數，而分類模型使用的是交叉熵損失函數，導致回歸模型的收斂速度比分類模型慢(Golik et al，2013)。

微地震的3種極性標簽相互獨立，屬于無序性問題，構建CNN的極性分類模型會比回歸模型更易于網絡結構的訓練和收斂。因此，本文在Tian等(2020)的基礎上，提出一種基于卷積神經網絡的地面微地震P波極性分類網絡模型，與MT-CNN類似，其輸入仍為多道記錄，但是輸出為中間道的極性。通過分析訓練模型的準確度、損失曲線以及在實際數據中的應用，進一步論證訓練模型的適用性。

1 數據預處理

本文使用的訓練數據為一套網格型的地面監測數據。地面監測的檢波器分布如圖1 所示，758個垂直單分量檢波器布置成由10條線所組成的網格，檢波器的間距約為25m，圖中的數字代表檢波器的排列順序。圖2(a)為時間長度為1s的原始波形，時間采樣率為1ms，原始數據的信噪比較低，難以肉眼識別出微震事件。通過對原始數據去除均值、帶通濾波(10～70Hz)，可觀測到較為清晰的微地震事件(圖2(b))。山西和順地勢復雜，檢波器高程在1290～1450m之間，通過高程校正，微震事件的記錄變得更加連續(圖2(c))，且可以觀察到極性逆轉的現象。

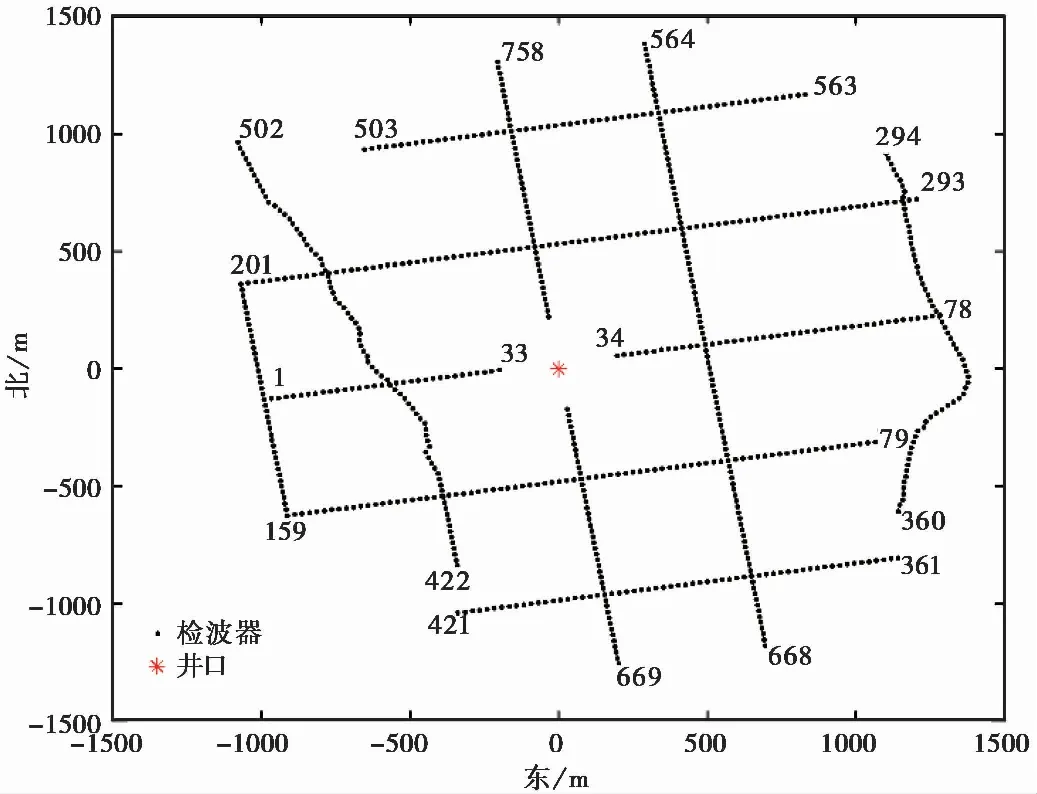
圖 1 地面微地震監測的檢波器分布

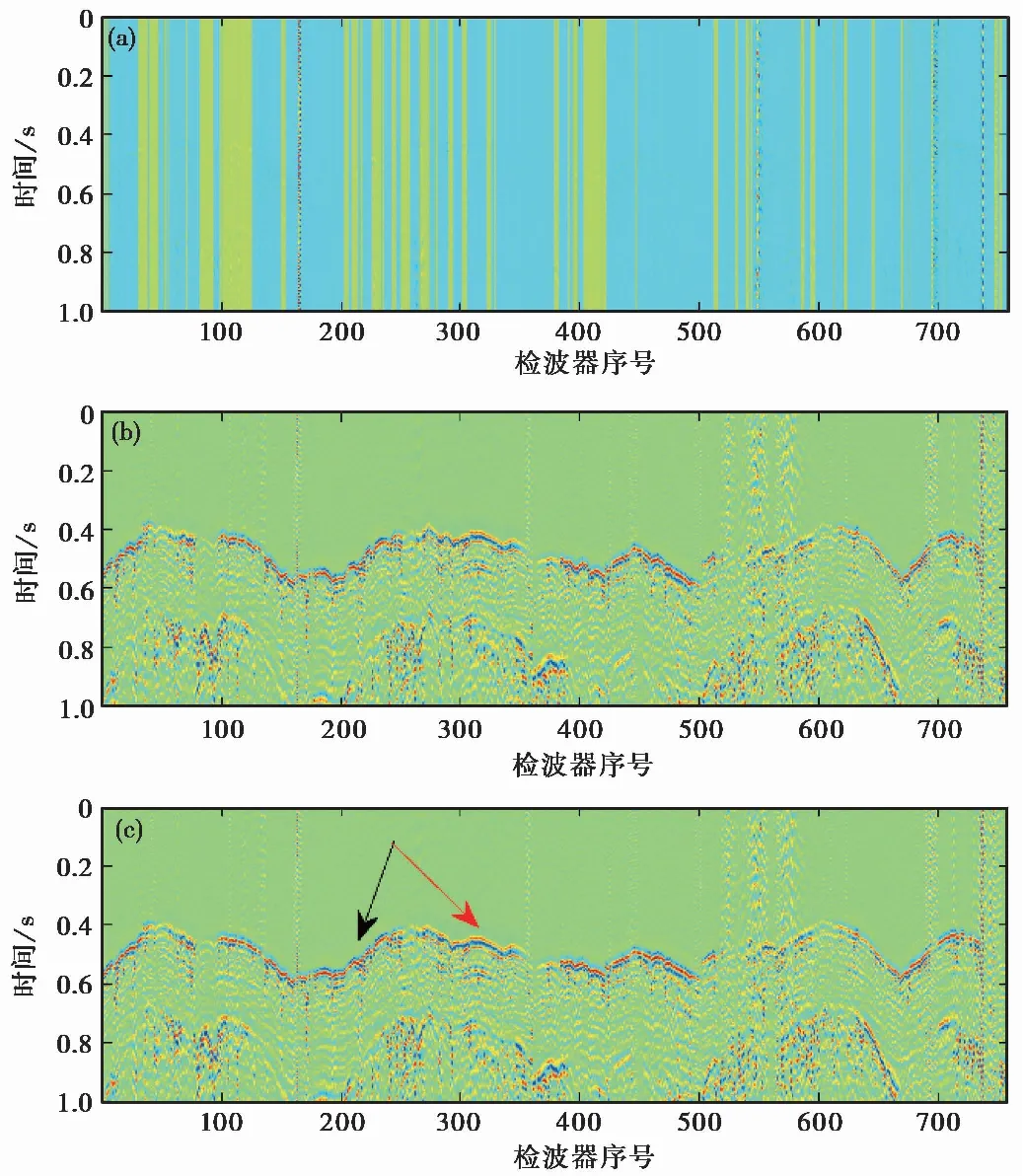
圖 2 微震數據預處理(a)觀測到的微震事件原始波形； (b)去除均值、帶通濾波(10～70Hz)后的波形； (c)高程校正后的波形； 紅色箭頭表示正極性，黑色箭頭表示負極性

通過對微地震原始數據預處理，最后挑選出具有不同震源機制解和信噪比的5個微震事件來構建數據集。為了提高訓練模型的泛化能力和魯棒性，對訓練樣本進行了數據增強(Tian et al，2020)。微震數據可以看作二維圖像數據，參照圖像識別，可使用反轉、平移的方式進行數據增強。反轉是指將已有的訓練樣本值乘以-1，相應的極性類型也反轉；平移是指沿著時間軸滑動樣本，使P波極性信息出現在時窗的任意位置。經過數據增強，數據集擴充為17227個樣本，其中正極性、負極性和不確定的比例分別為29%、39%和32%。最后將整個數據集和對應的標簽隨機分為2組：三分之二的數據用于模型訓練，稱為訓練數據集；剩余三分之一的數據用于模型測試，稱為測試數據集。

2 網絡結構

CNN是一個多層前饋神經網絡，卷積層作為CNN的關鍵部分，通常與其他層一起使用。CNN每個卷積層由一組濾波器組成，這些濾波器對前一層的輸出結果進行卷積計算，以此來提取數據集的P波極性特征并用于極性預測。通過優化學習過程和網絡結構，微調整個網絡的權重和偏差，可以最大限度地提取這些特征。本文基于Keras平臺分別設計了基于單道記錄的CNN模型和基于多道記錄的CNN模型，用于進行地面微地震P波極性分類。

2.1 基于單道記錄的CNN模型(ST-CNN-classify)

P波初至極性識別可以當作一個簡單的圖像分類問題。根據人工極性的識別結果，可將每道微震數據分為三類：正極性、負極性和不能被人工識別的不確定極性。基于單道記錄的CNN模型(簡稱ST-CNN-classify)截取單道地震記錄的P波信息作為輸入層，輸入樣本的大小為1×M的向量，其中1代表道數，M為時間域采樣點的個數。輸入樣本經過若干個相互交替的卷積層、池化層提取極性特征后，再經過一個或一個以上的全連接層，最后由 Softmax 分類器輸出3個值，分別對應輸入樣本為不確定、正極性、負極性的概率，其中最大概率值所對應的類別即為該網絡的預測結果，如圖3(a)所示，圖中輸出的最大概率值為0.92，對應極性類別為2，即極性為負。

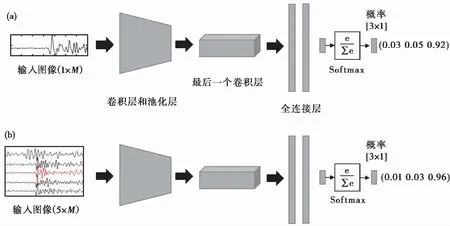
圖 3 基于單道記錄(a)與基于多道記錄(b)的極性分類網絡

分類問題一般采用交叉熵損失函數來優化網絡參數，交叉熵通常用于衡量輸入(真實)概率分布p和預測概率分布q之間的差異

(1)

其中，N為訓練數據集的大小。損失函數(Loss)可使用隨機梯度下降算法迭代求解，每次迭代后，卷積核和權重將會被更新。在訓練過程中，損失值(loss)和準確度(accuracy)為判斷ST-CNN-classify模型的性能指標。

2.2 基于多道記錄的CNN模型(MT-CNN-classify)

對于地面微震監測，檢波器陣列通常采用“星型”、“網格型”等規則觀測系統。考慮到P波的輻射花樣，相鄰檢波器記錄通常顯示出規則的極性分布。基于此，本文提出利用多條相鄰道的P波信息作為訓練樣本。為了將多道極性識別仍當作分類問題處理，輸入樣本包含多道相鄰檢波器記錄(道數為奇數)，但是只輸出中間道(目標道)的極性類型(圖3(b))。對于第K道的檢波器記錄，選取前后各N1道數據，時間域的采樣點數為M，則輸入樣本的大小為(2×N1+1)×M，輸出結果為第K道的極性。多道記錄和單道記錄的樣本標定方法相同，不確定為0，正極性為1，負極性為2。

MT-CNN-classify和ST-CNN-classify均為分類模型，兩者的區別主要在于前者能夠將目標道與相鄰道結合起來預測目標道的極性類型。如果目標道前面或后面不足N1道時，則填充目標道的波形記錄。與ST-CNN-classify相同，MT-CNN-classify也經過若干卷積層、池化層和全連接層，最后由Softmax分類器輸出不同類別的概率值，數值最大的概率值對應類別則為分類結果。

3 結果

3.1 訓練過程和網絡性能

利用微地震實際數據分別訓練2個CNN模型，其中MT-CNN-classify的訓練樣本中相鄰檢波器個數為5。在輸入神經網絡前，所有輸入數據均歸一化至[-1，1]之間。ST-CNN-classify 和 MT-CNN-classify 均使用4組卷積層，每組卷積層包含卷積最大池化和Dropout。其中，卷積操作通過ReLu激活函數實現從輸入數據中提取極性特征；在卷積層之后緊跟著最大池化層，其主要功能為降維、對特征進行壓縮、簡化網絡復雜度等；Dropout層是指按照一定概率將神經元從網絡中丟棄，從而降低模型的過擬合風險。卷積神經網絡的最后一層為全連接層，其用于連接所有的輸出，并用Softmax激活函數計算分類概率。2個CNN模型的網絡結構參數如表1、表2 所示。MT-CNN-classify和ST-CNN-classify結構相似，但在 MT-CNN-classify 中，卷積操作使用二維卷積核同時學習P波極性特征和檢波器陣列的極性規律。2個CNN網絡均采用隨機梯度下降優化方法進行訓練，學習率設定為0.01，模型設定的批量大小為8，迭代次數為200。

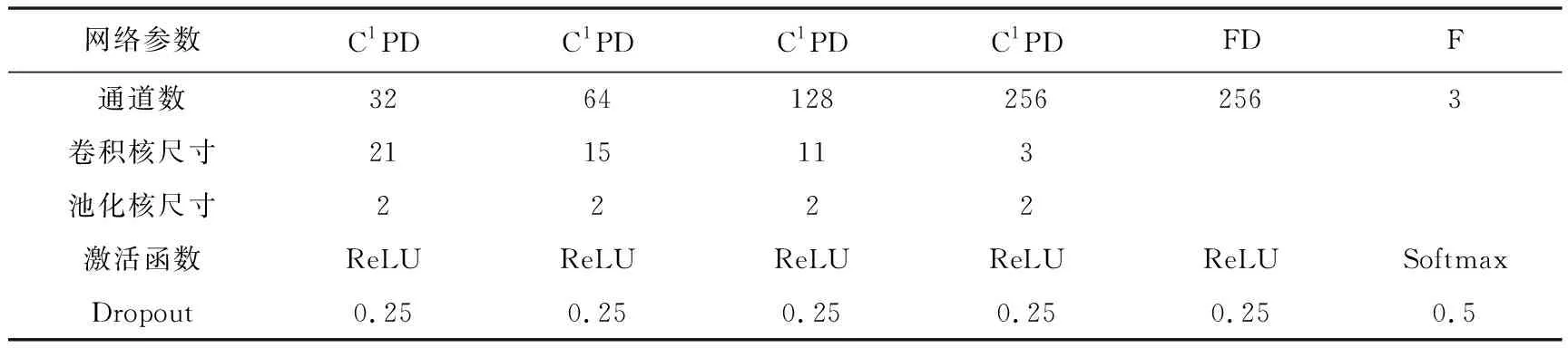
表1ST-CNN-classify參數

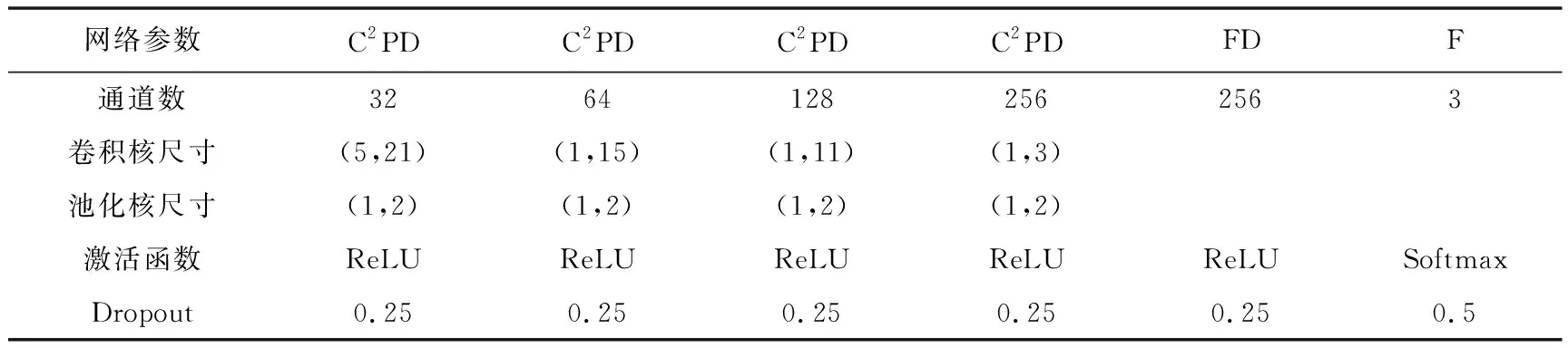
表 2MT-CNN-classify參數

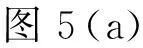
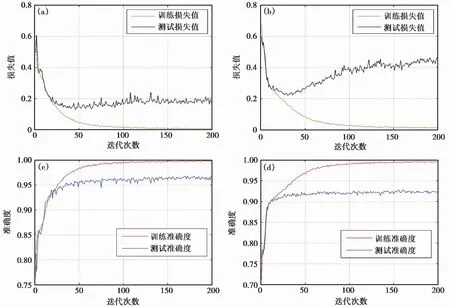
圖 4 MT-CNN-classify(a)、(c)和ST-CNN-classify(b)、(d)的準確度損失曲線訓練準確度和訓練損失曲線分別以紅色和綠色繪制；測試準確度和測試損失曲線分別以藍色和黑色繪制

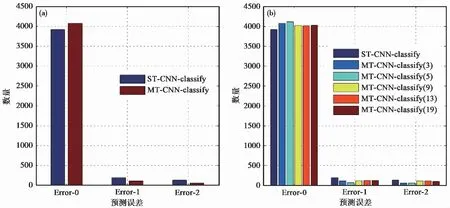
圖 5 測試數據集的預測誤差直方圖(a)測試集預測誤差分布；(b)不同數量檢波器的模型預測誤差對比

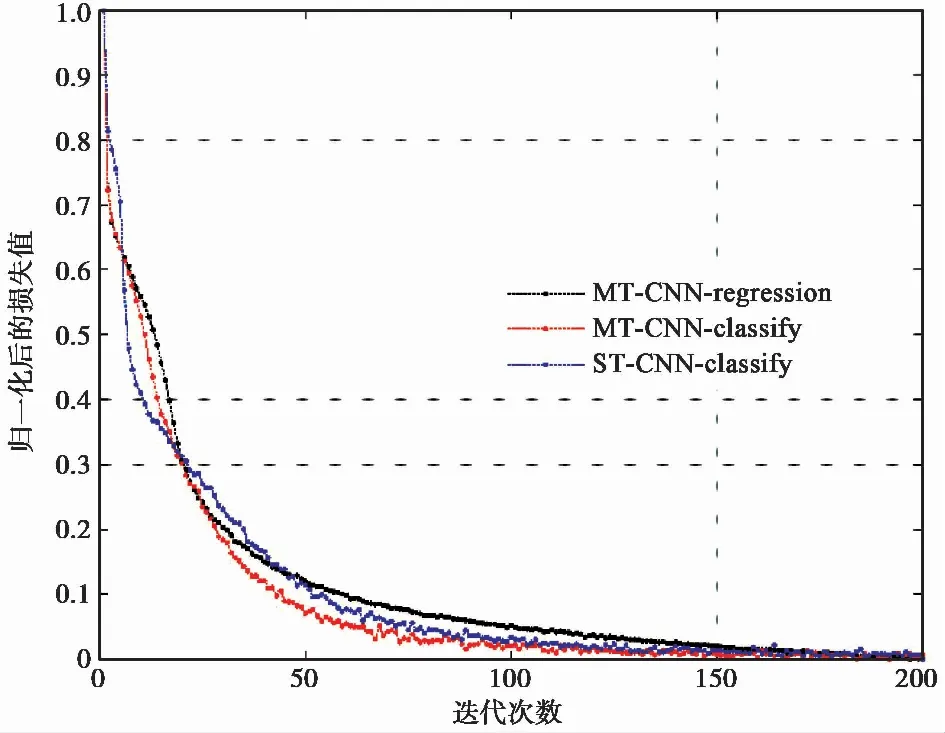
圖 6 3個CNN模型的損失曲線對比

3.2 實際數據應用

訓練好的CNN模型可進一步用于地面微震實際數據的P波極性分類。采用訓練好的ST-CNN-classify模型和MT-CNN-classify模型分別預測未用于構建訓練數據集的34個微地震事件的P波極性，預測過程僅耗時幾秒。由于實際數據的極性是未知的，可通過反演震源機制解來評估預測結果。利用P波極性求解震源機制解需要震源位置，在進行地面監測時，垂直單分量檢波器的P波記錄通常顯示出比S波更高的信噪比，因此可用P波信息定位微地震事件。根據已有的資料，用于繞射疊加定位的P波速度模型為4250m/s。X、Y、Z三個方向的定位范圍分別為0～1000m、0～1000m和700～1700m，步長均為10m。求出震源位置后，通過對所有可能的走向、傾角和滑動角進行格點搜索，可以得到最佳的震源機制解。最小矛盾比為CNN預測極性和震源機制解計算的極性不一致的比例，可用來評估反演得到的震源機制解的準確度。

圖 7對比了ST-CNN-classify模型和MT-CNN-classify模型預測的8個微地震事件的極性分布，極性預測結果直觀地顯示在檢波器陣列上，紅色、綠色和黃色圓圈分別為正極性、負極性和不確定，圓圈的大小與微震數據振幅的相對大小成正比，黑色實心圓代表了微震事件的震源位置，由繞射疊加方法利用極性矯正后的波形獲得。圖7 各分圖左上角的沙灘球(最佳斷層面解的下半球投影圖)是由預測的P波極性反演的震源機制解，黑色陰影區域代表壓縮象限，白色區域代表膨脹象限。通常，正極性應該被投射到壓縮象限，而負極性應該被投射到膨脹象限，然而ST-CNN-classify的膨脹(壓縮)象限中出現一些正(負)極性。對比圖7(a)和圖7(b)，可以直觀地看出MT-CNN-classify模型在正、負極性之間的預測誤差更小，得到的極性分布比ST-CNN-classify模型更為合理。圖7 中的Ψ為震源機制解的最小矛盾比，范圍在0和1之間，Ψ的數值越小，表明震源機制解越準確。Ψ值進一步證明了MT-CNN-classify模型具有更高的P波極性預測準確度。

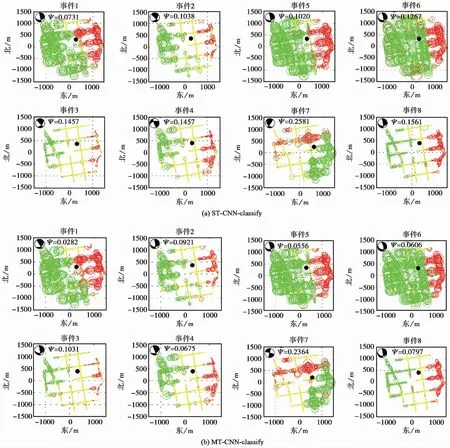
圖 7 8個微震事件的極性預測結果

統計34個微震事件的最小矛盾比的分布情況，如圖8 所示，圖8 中3種模型最小矛盾比的均值和方差見表3。結果表明，MT-CNN-classify模型的最小矛盾比大多分布在0～0.1區間，與ST-CNN-classify結果相比有較大改善。進一步對比基于回歸模型的 MT-CNN-regression 的結果(Tian et al，2020)，MT-CNN-classify中有13個事件的最小矛盾比在0～0.05區間，而MT-CNN-regression模型有11個事件在該區間。此外，相比ST-CNN-classify，多道數據的分類模型和回歸模型均有較低的最小矛盾比。

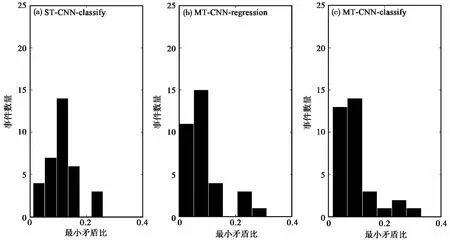
圖 8 不同CNN模型的最小矛盾比分布直方圖

表3不同CNN模型最小矛盾比的平均值和方差

4 討論

為了便于與Tian等(2020)中MT-CNN-regression的結果對比，本文構建數據集的方法與Tian等(2020)相同，但該處理方法存在數據泄露的風險。首先，將5個微震事件數據增強后的樣本分為訓練集與測試集，導致測試集與訓練集中可能存在同一源數據生成的樣本。此外，訓練樣本與測試樣本均來自5個微震事件，而檢波器為間距極小的高密臺陣。因此，對同一事件，相鄰臺站的波形記錄相似度極高，即訓練集與測試集中存在高度相似的樣本。

針對以上兩點，對檢波器個數為9的MT-CNN-classify網絡進行交叉驗證，即將5個微震事件數據增強后的結果依次放入訓練集和測試集，該處理方法可避免測試集與訓練集中存在同一源數據生成的樣本。5組樣本集交叉驗證的訓練集和測試集的準確度如表4 所示，結果表明，訓練集的準確度和圖4 相比相差不大，但測試集準確度有所降低，由此可證明圖4 所采用的數據集存在數據泄露。此外，最后一組交叉驗證的測試集準確度為74.58%，相比前面4組較低，這是由于事件5的信噪比較低。雖然本文使用的數據集存在數據泄露，導致測試集的準確度偏高，但是通過實際數據的應用，MT-CNN-classify模型比ST-CNN-classify的預測精度高這一結論仍然成立。

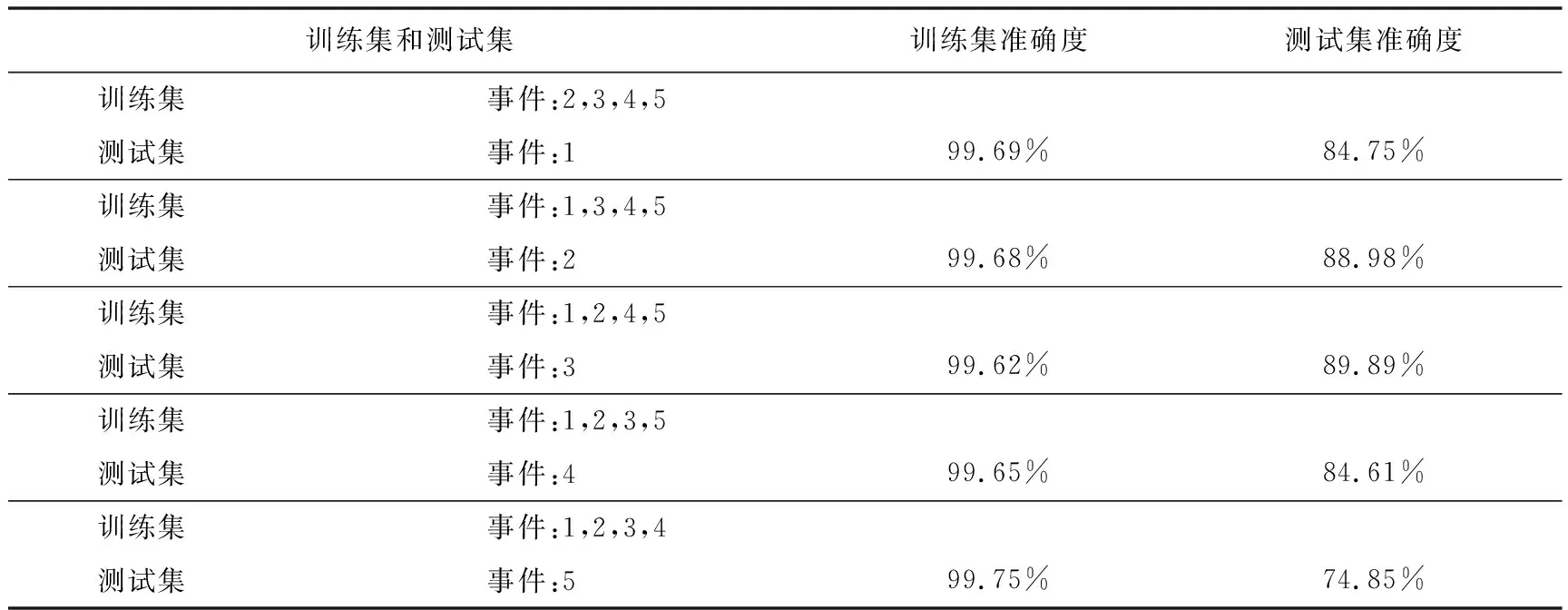
表4MT-CNN-classify交叉驗證

5 結論

針對地面微地震監測多為規則觀測系統，本文提出了基于卷積神經網絡的多道極性分類網絡模型，并以此來確定微震數據的P波極性。多道數據的卷積神經網絡模型不僅可以學習P波極性特征，還能夠學習相鄰檢波器的P波極性分布規律，進一步提高目標道的預測精度。本文著重對比了ST-CNN-classify、MT-CNN-classify和MT-CNN-regression三個網絡模型，實際數據的P波極性預測結果表明，相比單道數據的CNN模型，無論是基于回歸模型還是分類模型的多道數據的CNN均可獲得較高的極性預測精度。此外，MT-CNN-classify模型的損失曲線比MT-CNN-regression收斂快。本研究提出的基于多道的P波極性分類網絡還適用于其他具有規則臺站分布的地震數據集。

致謝：感謝南京物探研究院提供的水力壓裂監測數據以及審稿人提出的寶貴意見。