基于Geogebra的中職數學可視化教學實踐

袁蘭蘭

摘 要：本文以Geogebra軟件在中職數學中發揮的可視化功能為切入口，從數學問題可視化、數學猜想可視化以及數學概念可視化三個方面進行實踐研究，將中職數學中比較抽象、空間度較強的知識點以一種動態的過程演變、可視化的形式進行最終呈現，使學生理解知識的原理，真正掌握知識點，更好地進行知識正遷移。

關鍵詞：Geogebra? ? 可視化? ? 中職數學

Geogebra自2006年正式發布后，在數學教育界得到越來越多的認可。Geogebra支持幾何、代數、統計、微積分等教學，幾乎覆蓋整個數學教學領域。借助該軟件，教師可以設計更直觀的教學方式，為學生創造更直觀的學習環境。

一、數學問題可視化

數學探究的源頭是問題，教師利用Geogebra的動態演示功能為學生創設易于認識問題的良性認知環境，將數學問題以動態的方式呈現在學生面前，使數學問題更具直觀性和形象性，便于激發學生的學習興趣，從而高效地提出問題和解決問題。

（一）軌跡追蹤，理解數學問題

案例1.集合的交

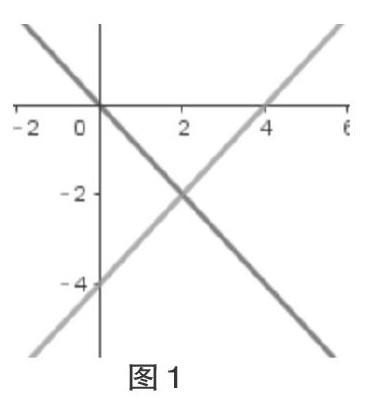
問題：設集合A={（x，y）|x+y=0}，┤集合B={（x，y）|x-y=4}，┤求A∩B。

集合的交是中職數學第一章第三節的內容，主要引導學生掌握三類集合的交集求法，其中點集的交是一個難點，學生普遍不理解問題中的點集具體是什么，更無從求解點集的交。運用Geogebra中的軌跡追蹤功能，就能形象地展示出集合A、B中的所有點（見圖1），學生通過觀察得出求點集的交只需求方程組的解。

（二）視圖變換，掌握數量關系

案例2.球的表面積與體積

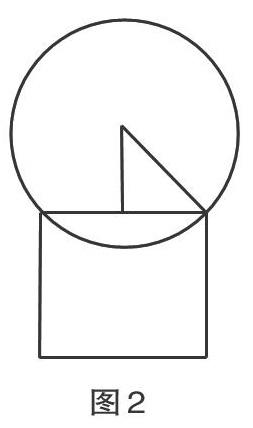
問題：把一個半徑為R的球放入棱長為4的正方體中，測得球底距正方體底面為3，求球的半徑R。

球是中職數學第九章第五節的內容，由于學生空間想象能力普遍較弱，不能較好理解題意，所以教師可以運用Geogebra中的三視圖功能，從不同角度向學生展示題干中的數量關系。首先，以直觀圖的方式引導學生直觀理解問題;變換角度，從上方俯視，學生進一步理解球與正方體的截面是圓且是球的小圓;從前方正視，學生清晰地看到一個直角三角形（見圖2），從而引導學生輕松解決問題。

二、數學猜想可視化

猜想是數學探究教學過程中的一個重要環節，可以提升學生的想象力和創造力。教師對學生的猜想不能輕易地加以肯定與否定，要用科學的態度來對待學生的猜想與發現。教師可以運用Geogebra對學生的部分猜想進行驗證，從而提高學生參與課堂互動的積極性，擴大學生的知識面，促進數學創造力的形成。

案例3.球的體積公式

（一）靜態展示，直接猜測結論

師：觀察三個等底等高的圓柱、半球、圓錐的體積關系。

師：寫出圓柱和圓錐的體積公式。

師：根據三個等底等高的圓柱、半球、圓錐的體積關系，猜想半球的體積公式。

（二）動態截圖，直觀驗證猜想

在Geogebra的3D繪圖區繪制等底等高的圓柱、圓錐以及半徑與圓柱高相等的球。

師：我們用一個平面去截球和圓柱中挖去圓錐（同底等高）這兩個幾何體（見圖3），截面分別為什么圖形？

生4：圓、圓環。

師：拖動截面，在運動的過程中，觀察截面（圓與圓環）的面積關系。

生5：在運動過程中，圓與圓環的面積始終相等，因此，上述半球體積等于柱體體積減去錐體的體積。

三、數學概念可視化

數學概念是數學知識的基礎，是學生學好數學命題、數學原理、解決數學問題的關鍵所在。通過可視化的教學方式，教師可以幫助學生將隱性的數學知識顯性化，將抽象的數學概念形象化，便于學生從系統的角度把握數學概念之間的聯系。

（一）改變平面位置，體驗概念相互關系

案例4.橢圓的定義

平面內到兩定點距離之和為常數（大于兩定點間距離）的點的軌跡為橢圓。在古希臘時期，人們通過用平面去截立體圓錐得到橢圓，拖動滑桿改變平面位置，還可以得到雙曲線和拋物線，運用Geogebra可展示這一過程（見圖4），因此橢圓、雙曲線以及拋物線統稱為圓錐曲線。教師利用Geogebra將古希臘人認知圓錐曲線的過程可視化，展示三種曲線的起源，學生理解了為何三種曲線被統稱為圓錐曲線。

（二）轉變視圖方向，理解數學概念本質

案例5.二面角的平面角定義

以二面角的棱上任意一點為端點，在兩個面內分別作垂直于棱的兩條射線，這兩條射線所成的角叫作二面角的平面角。

空間想象能力較弱的學生理解二面角的平面角定義是有一定困難的。教師借助Geogebra的動態展示，引導學生理解定義的三個關鍵點：第一，公共棱上任取一點;第二，過點分別在兩個半平面內作公共棱的射線;第三，兩射線所成角。通過改變點A的位置，學生觀察發現角度始終不變，明白點A的選取不影響二面角的平面角的值，真正理解“任取”的緣由（見圖5）;改變視角，教師引導學生直觀感受平面角;固定平面BPQ，讓平面CPQ繞著公共棱PQ旋轉，觀察得出平面角的范圍為。

課堂實踐證明，將Geogebra應用到中職數學課堂教學，利用Geogebra輔助講解，學生更容易認識數學問題、檢驗數學猜想、掌握數學概念以及理解推理過程，學習興趣也得到激發。

參考文獻：

[1]崔麗萍.數學可視化教學及其若干范例[D].上海：上海師范大學，2006.

[2]曉霞.初中數學概念類知識的可視化研究[D].南京：南京師范大學，2014.

[3]范文貴.基于信息技術開展數學探究可視化的研究[J].中國電化教育，2008（259）.

（作者單位：嘉興技師學院）