加載速率影響下的巖石尺寸效應(yīng)及聲發(fā)射特征

張嘉凡，楊彥澤

(西安科技大學(xué)理學(xué)院，陜西 西安 710054)

0 引 言

巖石是非均質(zhì)地質(zhì)材料，具有非線性、非均勻性以及復(fù)雜性的幾何結(jié)構(gòu)[1]。巖石由于受大氣風(fēng)化作用和地質(zhì)因素的影響，其內(nèi)部含不同類型的空隙，表現(xiàn)出不同的物理性質(zhì)。不同尺寸的巖樣其力學(xué)性質(zhì)存在差異，即巖石材料尺寸效應(yīng)[2]。在不同應(yīng)力環(huán)境條件下，巖石力學(xué)參數(shù)存在差異，其中應(yīng)變速率與巖石的峰值強度、峰值前積聚能量、峰值后釋放能量呈正相關(guān)，對巖石力學(xué)參數(shù)的影響起主導(dǎo)作用[3]。隨著數(shù)值模擬技術(shù)的廣泛應(yīng)用，運用數(shù)值分析軟件去解決巖土工程問題日趨成熟。巖石破裂過程分析系統(tǒng)RFPA2D可實現(xiàn)巖石試件的加載破裂、巖石破裂的聲發(fā)射、裂紋擴展和相互作用的數(shù)值模擬。

國內(nèi)外有關(guān)學(xué)者一直在開展巖石尺寸效應(yīng)的理論研究，取得了豐碩的研究成果。楊圣奇等[4]、王軍祥等[5]，對巖石材料在不同圍壓條件下的尺寸效應(yīng)作了數(shù)值模擬,分析了巖石尺寸效應(yīng)與圍壓間的關(guān)系；王云杰等[6]利用RFPA2D，對炭質(zhì)泥巖單軸加的力學(xué)行為進行研究，采用高徑比為2的標(biāo)準(zhǔn)試樣進行模擬，發(fā)現(xiàn)150 mm×300 mm是巖石強度的分界點；梁正召等[7]建立了試樣尺度的概率模型，提出了一種細觀宏觀層次的跨尺寸的巖體參數(shù)計算思路；鐘波波等[8]利用RFPA2D，研究了裂紋分布形式，并對裂紋擴展的影響因素作了分析；張明等[9]、房智恒[10]對巖石力學(xué)試驗進行數(shù)值模擬，分析不同加載條件對巖石強度尺寸效應(yīng)的影響；劉剛等[11]開展了小尺度效應(yīng)下黃砂巖的單軸壓縮變形聲發(fā)射實驗，研究了小尺度效應(yīng)巖樣力學(xué)特性和聲學(xué)特征；王創(chuàng)業(yè)等[12]分析了不同尺寸巖樣在加載過程中的力學(xué)特性與聲發(fā)射信號變化特征。

綜上所述，目前對巖樣在單軸壓縮條件下的尺寸效應(yīng)研究已取得了一定的研究成果，但是巖石在不同加載速率條件下，其峰值強度及聲發(fā)射規(guī)律有所不同。因此，對巖石尺寸效應(yīng)、加載速率和聲發(fā)射規(guī)律等方面進行研究，對巖石工程中力學(xué)參數(shù)的設(shè)定具有一定指導(dǎo)意義，并對巖石工程災(zāi)害具有預(yù)防作用。鑒于此，本文運用RFPA2D數(shù)值模擬分析軟件，分析在不同尺寸條件下加載速率對巖石強度和聲發(fā)射的影響規(guī)律，分析巖石在單軸壓縮試驗中影響尺寸效應(yīng)的主要因素，揭示不同尺寸巖樣和加載速率對巖樣的強度與聲發(fā)射特征的影響規(guī)律。

1 模型建立

數(shù)值模擬試驗的力學(xué)參數(shù)的選取參照陜西侏羅紀(jì)煤田煤巖性質(zhì)選取(表1)，彈性模量Es為50 000 MPa，強度均值為200 MPa，均質(zhì)度系數(shù)為200，泊松比均值μs為0.2，內(nèi)摩擦角φ為30°，模型試樣信息見表2。對試樣進行單軸壓縮試驗，采用不同的加載速率進行加載，加載速率1為0.002 mm/步，加載速率2為0.003 mm/步，加載速率3為0.004 mm/步，加載速率4為0.005 mm/步，加載速率5為0.006 mm/步。試驗考慮巖石的尺寸效應(yīng)而非端部摩擦效應(yīng)，故加載均在沒有端部約束的理想狀態(tài)下進行，如圖1所示。

表1 模擬實驗所用力學(xué)參數(shù)Table 1 Mechanical parameters for simulation experiment

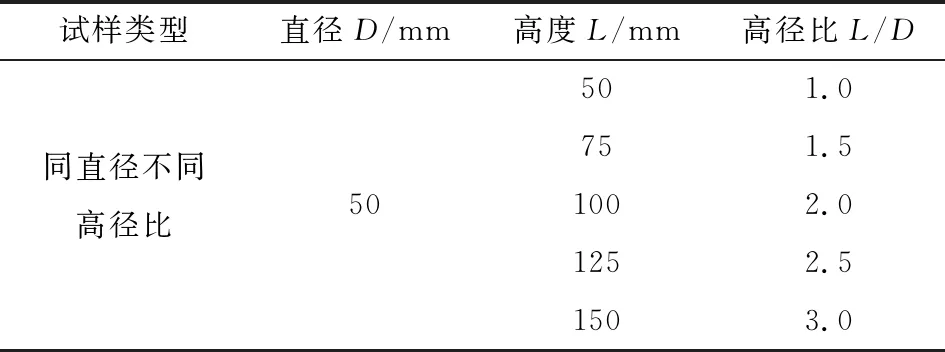
表2 不同尺寸試樣數(shù)值模擬參數(shù)Table 2 Numerical simulation parameters ofspecimens of different sizes

圖1 單軸壓縮實驗數(shù)值模型Fig.1 Numerical model of uniaxial compression experiment

2 數(shù)值模擬結(jié)果分析

2.1 不同高徑比模型在單軸壓縮時的應(yīng)力-應(yīng)變曲線對比分析

圖2為不同高徑比尺寸模型在單軸壓縮數(shù)值模擬時的應(yīng)力應(yīng)變對比分析圖。 從圖2中可以看出，在同一加載速率下，隨著試樣高徑比的增大，其峰值強度逐漸降低，具有一定的尺寸效應(yīng)。 試樣峰值強度前包括壓密、彈性與塑性階段，峰值強度之后，應(yīng)力迅速降低到殘余強度階段。 從加載速率為0.002 mm/步時的應(yīng)力應(yīng)變曲線可以看出，當(dāng)高徑比從1增加到3時，峰值強度從38.861 MPa降低至32.888 MPa，降幅為15.4%；從加載速率為0.006 mm/步時的應(yīng)力應(yīng)變曲線可以看出，當(dāng)高徑比從1增加到3時，峰值強度從46.962 MPa降低至41.521 MPa，降幅為11.6%，通過對比圖2不同加載速率時的應(yīng)力應(yīng)變曲線圖，峰值強度變化趨勢基本相似，但峰值強度降低幅度不盡相同。

圖2 不同高徑比模型單軸壓縮應(yīng)力-應(yīng)變曲線Fig.2 Uniaxial compressive stress-strain curves of different height-diameter ratio models

從圖3可看出，試樣的破壞主要在局部區(qū)域內(nèi)，這是由于巖石材料具有非均質(zhì)性，在應(yīng)力集中時產(chǎn)生局部變形。這種試樣局部化與實際效果基本一致，表明RFPA2D系統(tǒng)性能穩(wěn)定，應(yīng)用性較廣。同時，不同尺寸巖樣破壞形式不同，但主要為軸向破裂，并伴有局部剪切破壞。

圖3 不同高徑比巖樣破壞效果圖Fig.3 Failure effect of rock samples withdifferent height-diameter ratios

2.2 同高徑比模型在不同加載速率條件下單軸壓縮時的應(yīng)力-加載步曲線對比分析

從圖4可以看出，不同加載速率對試樣單軸壓縮時的峰值強度有一定程度的影響。不同加載速率下，同高徑比模型在單軸壓縮的模擬過程可分為壓密、彈性、塑性與破壞4個階段，且試樣破壞時的峰值強度隨加載速率的增大依次增高，峰值強度變化明顯。

對比圖4不同尺寸模型在單軸壓縮時的應(yīng)力應(yīng)變曲線圖，其峰值強度變化趨勢基本相同。整體看，當(dāng)ε≤0.003 mm/步時，試樣應(yīng)力-應(yīng)變曲線峰后階段應(yīng)力釋放相對平緩；當(dāng)ε>0.003 mm/步時，應(yīng)力釋放速度較快，出現(xiàn)應(yīng)力跌落現(xiàn)象，峰后段應(yīng)力-加載步曲線相對較陡。

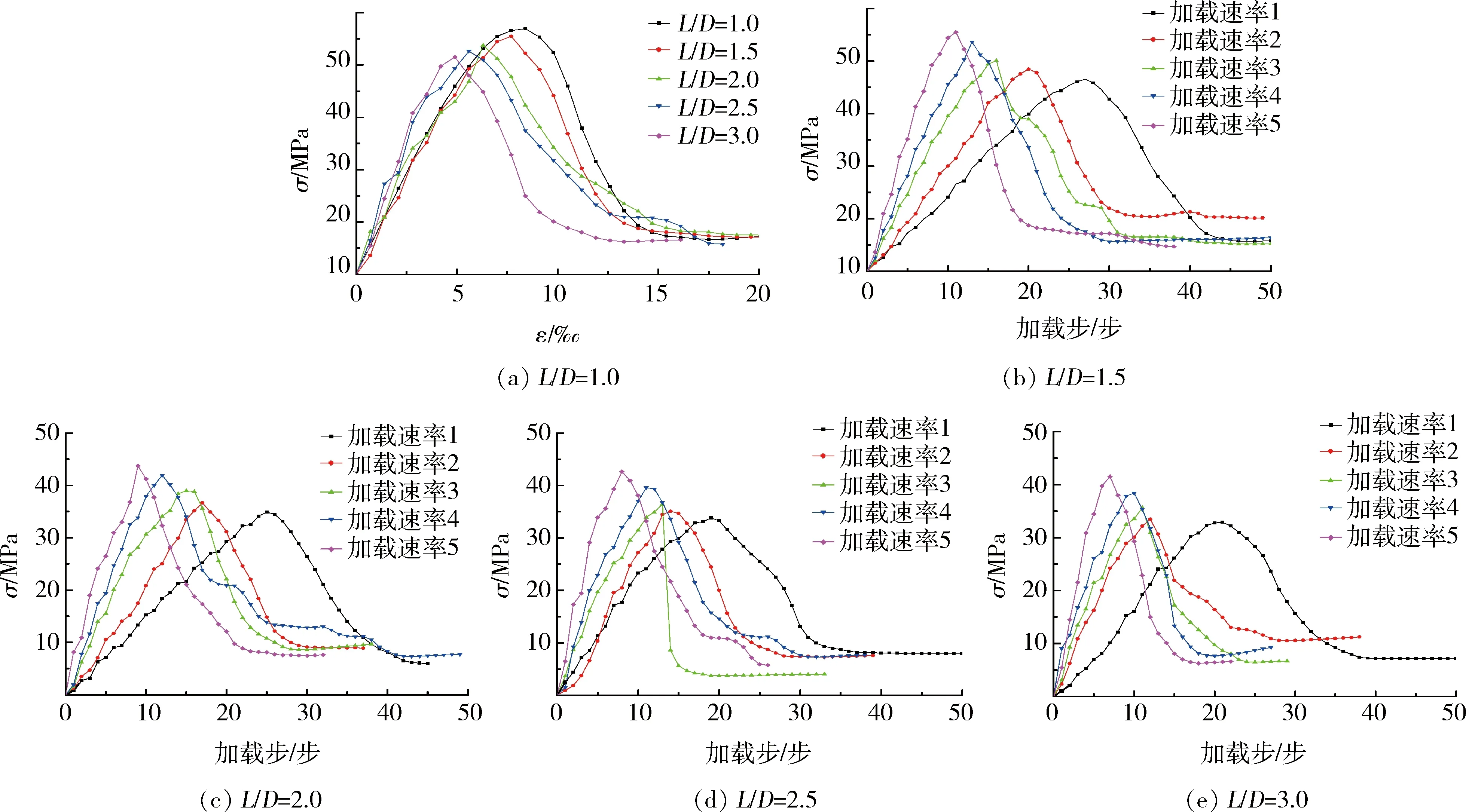
圖4 不同加載速率下試樣單軸壓縮試驗應(yīng)力-加載步曲線Fig.4 Stress-loading step curves of specimens under uniaxial compression at different loading rates

2.3 峰值強度與試樣高徑比的關(guān)系

圖5為峰值強度與試樣高徑比的擬合曲線。從圖5中可以看出，隨著試樣高徑比的增大，其在單軸壓縮時的峰值強度逐漸降低，最后曲線趨于平緩。隨著加載速率的增大，其峰值強度逐漸變大，曲線斜率也逐漸變大，說明試樣峰值強度尺寸效應(yīng)比較明顯。且當(dāng)L/D≥2時，試樣峰值強度降幅逐漸減慢，說明尺寸效應(yīng)逐漸減弱。對于不同擬合曲線進行縱向?qū)Ρ龋簭臄M合曲線1到5，其對應(yīng)的加載速率依次從0.002 mm/步增加至0.006 mm/步，峰值強度也隨之變大。且對于不同加載速率所對應(yīng)的擬合曲線，其變化趨勢基本一致，反映出巖石材料內(nèi)部弱化具有一定的均勻性。試樣峰值強度與高徑比的關(guān)系詳見表3。

表3 峰值強度與高徑比的關(guān)系Table 3 Relationship between peak strength and aspect ratio

圖5 試樣單軸壓縮時峰值強度與高徑比關(guān)系曲線Fig.5 Relationship between peak strength and aspectratio of specimens under uniaxial compression

2.4 加載速率與巖石峰值強度的關(guān)系

圖6為試樣單軸壓縮時峰值強度與加載速率的對比關(guān)系曲線。從圖6中可以看出，不同高徑比試樣的峰值強度隨加載速率的變化趨勢基本一致，但在不同加載速率條件下，L/D=1時，峰值強度最大；L/D=3時，峰值強度最小。且峰值強度的增加幅度也不相同，L/D=1時，峰值強度從38.86 MPa增加至45.96 MPa，增加幅度為18.41%；L/D=3時，峰值強度從32.98 MPa增加至36.72 MPa，增加幅度為11.36%。 整體看，當(dāng)加載速率ε≤0.003 mm/步或ε>0.005 mm/步時，隨著加載速率的增大，峰值強度的增幅較小，最終趨于穩(wěn)定，其關(guān)系曲線也比較平緩。 當(dāng)加載速率0.003 mm/步<ε≤0.005 mm/步時，隨著加載速率的增大，試樣峰值強度的增幅較大，關(guān)系曲線斜率相對較大。試樣加載速率與峰值強度的關(guān)系詳見表4。

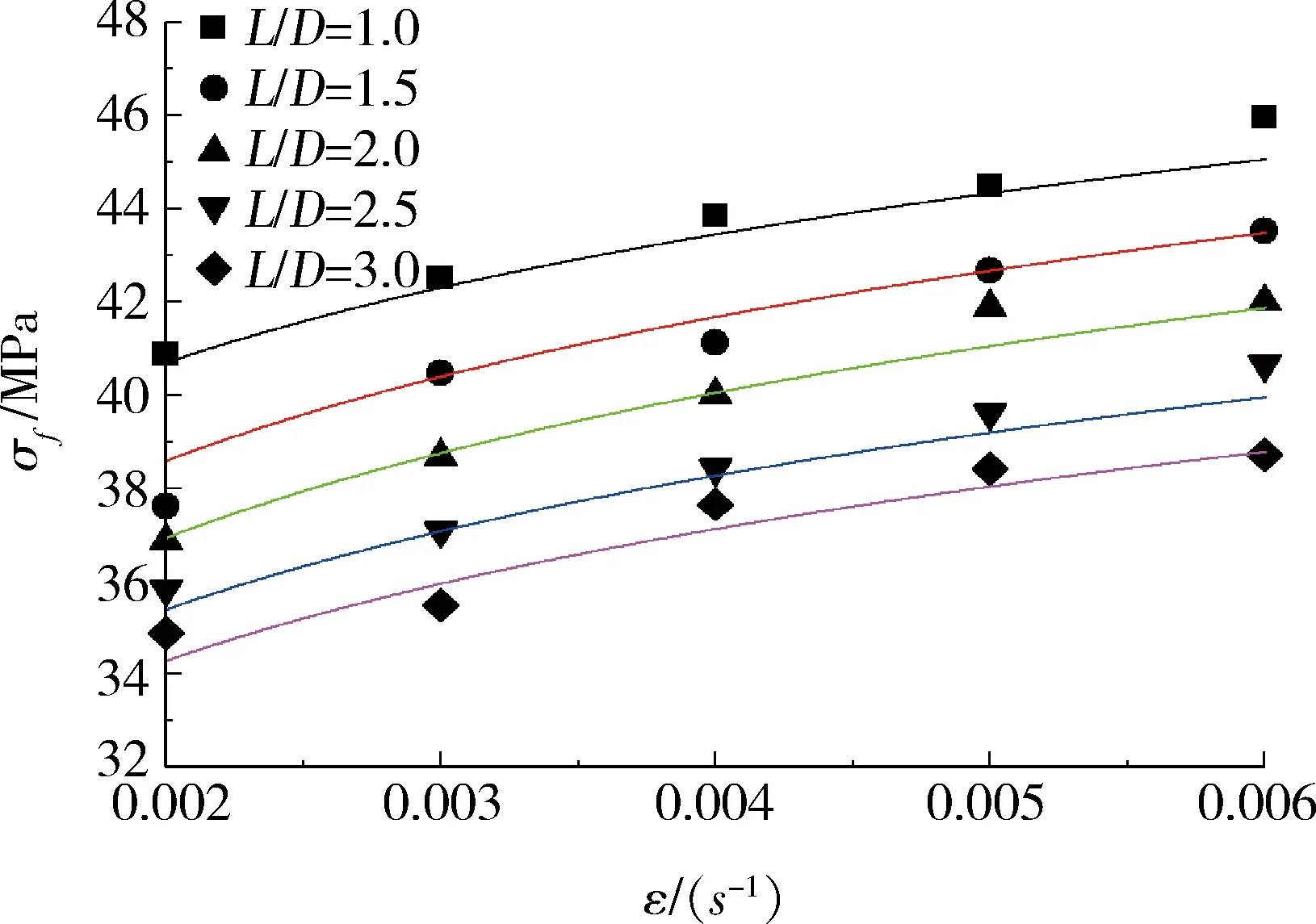
圖6 試樣單軸壓縮時峰值強度與加載速率關(guān)系曲線Fig.6 Relation curve between peak strength and loadingrate of specimen under uniaxial compression

表4 加載速率與峰值強度的關(guān)系Table 4 Relationship between loading rateand peak strength

2.5 不同尺寸模型在同一加載速率時的應(yīng)力-聲發(fā)射曲線對比分析

尺寸效應(yīng)對試樣破壞過程產(chǎn)生影響，而聲發(fā)射可以作為監(jiān)測試樣內(nèi)部破裂損傷的主要手段，通過對不同尺寸試樣在單軸壓縮過程中的聲發(fā)射特征進行研究分析，可進一步揭示尺寸效應(yīng)內(nèi)部機理[16]。同樣，RFPA可以進行聲發(fā)射數(shù)值模擬，在軟件后處理設(shè)置中，可以顯示計算后聲發(fā)射場圖，同時可以導(dǎo)出對應(yīng)的聲發(fā)射數(shù)據(jù)，可以對數(shù)據(jù)進行處理得到不同類型的聲發(fā)射圖。趙康等[13]通過RFPA2D對不同尺寸巖樣進行數(shù)值模擬，分析研究了聲發(fā)射產(chǎn)生的時間序列和空間分布關(guān)系及規(guī)律特征。

基于此，通過RFPA2D模擬聲發(fā)射，研究其特征規(guī)律能很好的反映尺寸效應(yīng)特征。因不同加載速率下應(yīng)力-聲發(fā)射曲線特征基本一致，這里只討論分析不同高徑比模型在加載速率為0.003 mm/步時的應(yīng)力-聲發(fā)射曲線，如圖7所示。加載初期由于荷載較小，處于壓密階段，在此過程中的少量微觀裂隙，在受到軸向壓力作用下逐漸被壓實并封閉，它需要吸收能量，該階段只有一些低能量的小聲發(fā)射事件發(fā)生，聲發(fā)射數(shù)極少或基本沒有；在彈性階段，產(chǎn)生可恢復(fù)的彈性變形，試樣所受載荷不足以形成新的微裂紋，此時聲發(fā)射數(shù)有所增加；在塑性階段，裂紋開始產(chǎn)生并不斷蓄積，導(dǎo)致不可逆的塑性變形，巖石的非彈性體積應(yīng)變不斷增加，發(fā)生膨脹現(xiàn)象，在次階段，試樣聲發(fā)射事件活動開始活躍，并且隨著應(yīng)力的增加，聲發(fā)射的振鈴次數(shù)增加，因此該階段稱為聲發(fā)射的活躍期。隨著加載位移繼續(xù)增大，在峰值強度前后，試件出現(xiàn)大面積裂紋，聲發(fā)射振鈴數(shù)產(chǎn)生突變，可將其作為巖樣失穩(wěn)破壞的前兆；在峰后階段，試樣出現(xiàn)大量宏觀裂紋后，應(yīng)力曲線迅速下降，其加載強度隨之降低，聲發(fā)射儀所檢測能量也隨之降低，故聲發(fā)射數(shù)也逐漸遞減，最后到完全沒有聲發(fā)射出現(xiàn)，將該過程稱之為衰減期。總體看，當(dāng)試樣高徑比L/D≤2時，聲發(fā)射數(shù)在峰值強度后較多，整個過程呈現(xiàn)出“先逐漸增多后逐漸減少直至遞減為0”的漸進型變化規(guī)律；當(dāng)L/D>2時，聲發(fā)射數(shù)較少，在峰值強度之后出現(xiàn)很明顯的聲發(fā)射事件，屬于突躍型變化規(guī)律。同時，通過振鈴計數(shù)可以較直觀確定巖石單軸壓縮過程中的應(yīng)力閾值。

圖7 不同高徑比模型單軸壓縮時應(yīng)力-聲發(fā)射曲線Fig.7 Stress-acoustic emission curves of differenteight-diameter ratio models underuniaxial compression

3 結(jié) 論

1) 在同一加載速率下，隨著試樣高徑比的增大，其峰值強度逐漸降低，具有尺寸效應(yīng)。試樣峰值強度前包括壓密、彈性與塑性階段，峰值強度之后，應(yīng)力迅速降低到殘余強度階段。同時，不同加載速率對試樣單軸壓縮時的峰值強度有一定程度的影響，試樣破壞時的峰值強度隨加載速率的增大依次增高，峰值強度變化明顯。

2) 峰值強度與試樣高徑比的關(guān)系、峰值強度與加載速率的關(guān)系均可用關(guān)系式進行描述。 當(dāng)L/D≥2時，試樣峰值強度降幅逐漸減慢，說明尺寸效應(yīng)逐漸減弱。在不同加載速率條件下，L/D=1時，峰值強度最大；L/D=3時，峰值強度最小。且當(dāng)加載速率0.003 mm/步<ε≤0.005 mm/步時，隨著加載速率的增大，試樣峰值強度的增幅較大，尺寸效應(yīng)比較明顯。

3) 當(dāng)試樣高徑比L/D≤2時，聲發(fā)射數(shù)在峰值強度后較多，整個過程呈現(xiàn)出“先逐漸增加后逐漸減少直至遞減為0”的漸進型變化規(guī)律；當(dāng)L/D>2時，聲發(fā)射數(shù)較少，在峰值強度之后出現(xiàn)很明顯的聲發(fā)射事件，屬于突躍型變化規(guī)律。因此，根據(jù)不同尺寸巖石試樣的聲發(fā)射時間序列和空間分布特征關(guān)系，對利用聲發(fā)射特性來預(yù)測尺寸效應(yīng)下不同尺寸巖樣破裂來臨及其位置有一定的參考意義。