不同幾何特征結構面巖體沖擊動態響應的數值模擬研究

張 飛，張東賓，王宇偉

(中國礦業大學(北京)力學與建筑工程學院，北京 100083)

0 引 言

在地礦開采過程中，往往對巖體施加爆炸、沖擊等強動荷載作用使其破碎，而巖體中富集的結構面影響其動態力學行為，給工程活動的順利進行帶來了諸多困擾。巖體中的結構面形式多樣，如孔洞、節理、裂隙等，其幾何特征對巖體的力學特性影響也各有不同。眾多學者對含結構面巖體的動態力學特性開展了廣泛的研究工作。

譚卓英等[1]對含圓形孔洞結構面巖體的沖擊動態響應進行了實驗模擬研究，結果表明孔洞結構對巖體沖擊破壞形式、峰值應力水平等有一定影響。朱哲明等[2]對含缺陷巖體的爆炸動態響應進行了研究，發現不同缺陷種類的巖體動態強度和破壞范圍有所差別。楊仁樹等[3]通過實驗分析了含貫通裂紋的類巖石介質動態破裂行為和預應力場中含層理類巖石介質爆破破裂的動態響應。王蒙等[4]基于SCSCC試件對巖石復合型裂紋的動態擴展特性進行了實驗研究。YAVUZ等[5]對含多裂紋無限大平板進行分析，得出裂紋間距和長度對應力強度因子的影響規律，并給出應力強度因子計算式。GREGOIRE等[6]在進行沖擊試驗時發現動態裂紋擴展時有止裂又繼續擴展的現象。ZHU等[7]對巷道圍巖的動態響應問題進行了數值模擬和實驗研究，并分析了應力波作用下的動態響應及加載方式對動態響應的影響。AVACHAT等[8]對巖體的動態斷裂行為引入高速攝影法進行了影像學分析。FUNATSU等[9]在分析巖體斷裂破壞時，考慮了壓力和溫度等因素對砂巖動態破壞的影響。魏晨慧等[10]和謝冰等[11]對節理角度和間距變化時的巖體爆炸動態響應進行了數值模擬研究。以上諸多研究從多個角度對巖體的動態力學行為進行了研究，分析了動態應力強度因子、裂紋擴展行為等動力學特性。本文基于ABAQUS數值分析平臺，建立模型，分析巖體結構面幾何特征變化時的沖擊動態響應，以期找到結構面幾何特征對巖體沖擊動態響應的影響。

1 應力波衰減規律

應力波在巖體等非連續性介質中傳播時，往往受地質條件、結構面幾何特征等因素影響，其反射透射及衰減狀況尤為復雜，眾多學者提出了一些理論模型，如接觸界面模型、完好黏結界面模型、位移不連續體模型等。基于這些理論模型，應力波經過非連續界面時的傳播規律了較為完善的理論支撐，如李業學等[12]推導了應力波穿越節理時反射透射系數FR1、FT1的解析解，其受節理等效剛度、波阻抗、頻率等因素影響，見式(1)和式(2)。

(1)

(2)

應力波在巖體中傳播時，受到阻滯作用發生衰減，攜帶能量耗散；巖體某一質點位移表示為式(3)。

u(x,t)=Aei(ωt-Ux)

(3)

其中：

(4)

(5)

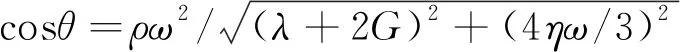
(6)

式中：A為質點振幅；λ為波長；G為剪切模量；η為黏滯系數；ρ為密度；ω為應力波頻率。

聯立式(4)～式(6)可得式(7)。

U=β-iα

(7)

其中：

α=

β=

將式(7)代入式(3)可得式(8)。

u(x,t)=Ae-αxei(ωt-βx)

(8)

由此可知，應力波在巖體中傳播時以式(8)的函數關系衰減，并且與巖體的黏滯系數、剪切模量、密度、應力波頻率等因素有關。

2 模型建立

巖體本構模型選擇德魯克-普拉格準則(以下簡稱“D-P準則”)作為失效準則。D-P準則同時量化了體積應力、剪應力和中間主應力對巖石彈塑性強度的影響，能理想地反映巖石的力學行為。

為分析巖體結構面幾何特征不同時沖擊荷載作用下的動態響應，建立A組、B組、C組三組模型。平面應力狀態如圖1所示，外觀尺寸150 mm×50 mm，上部中點受沖擊荷載，速度30 m/s，下部及左右部設置為約束邊界，x、y、z方向位移為0；網格劃分時，單元形狀為四邊形，采用進階算法(advancing front)生成均勻網格，單元屬性為四結點雙線性平面應力四邊形單元；為便于分析，取分析點及分析路徑，以A組模型為例，模型A1結構面左側端部分析點記為A1L，右側端部分析點記為A1R，下部中間分析點記為A1D，左右兩側以端部為起始點豎直向下方向上分別取分析路徑記為path1和path2，其他模型同理。

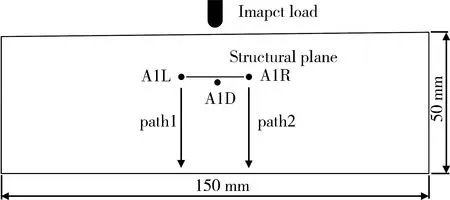
圖1 模型示意圖Fig.1 Diagram of model

選用ABAQUS/Explicit，其本質上是基于動力學方程求解，對于爆炸、沖擊的數值模擬具有很好的仿真效果。

3 結果分析

3.1 結構面厚度變化時的動態響應

A組模型的結構面厚度值分別為0.1 mm、0.2 mm、0.3 mm、0.4 mm，截取模型中間部分如圖2所示。

圖2 A組模型示意圖Fig.2 Diagram of group A model

四個分析點A1D、A2D、A3D、A4D的Mises應力值隨時間變化如圖3所示。以沖擊塊體接觸模型為零時刻，在70 μs左右時，Mises應力值出現峰值，分別為12.52 MPa、9.89 MPa、9.80 MPa、9.34 MPa。 模型A1結構面厚度為0.1 mm，分析點A1D的Mises應力峰值高于同組其他3個模型，但其他3個模型此時峰值差別不大，這可能是結構存在某一特定厚度使應力波沒有穿透結構面所導致。隨著時間的延后，分析點A1D的Mises應力值震蕩下降，在200 μs之前，其值基本上大于其他3個模型分析點，200 μs左右時，其他3分析點應力峰值高于分析點A1D，這是因為應力波發生繞射，導致結構面下部分析點處的應力值又有所上升，200 μs之后，Mises應力值震蕩下降。

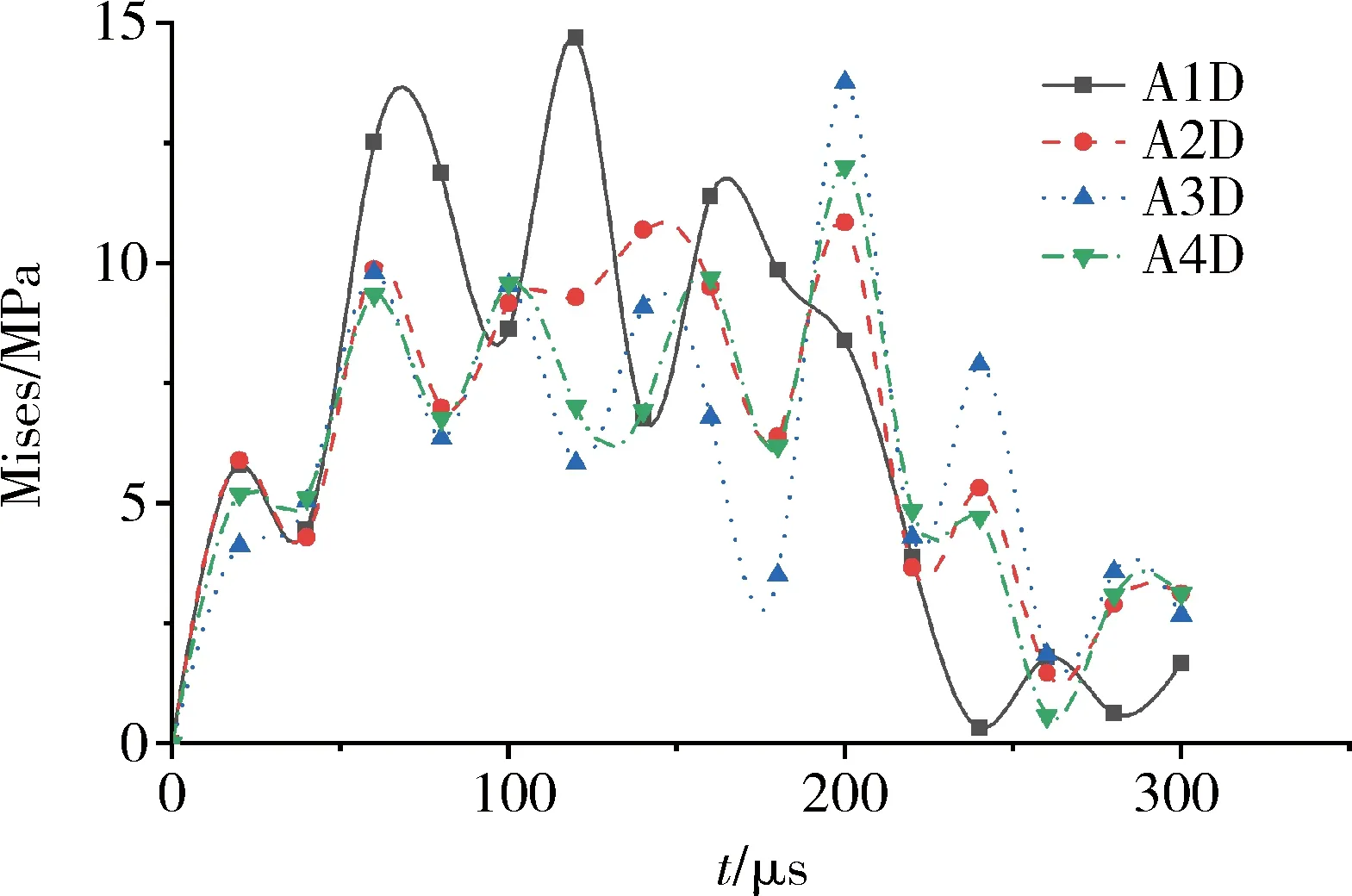
圖3 下部分析點應力值Fig.3 Stress of down monitoring point

以模型A1為例，在分析路徑path1上，其Mises應力值隨距離衰減曲線如圖4所示。擬合函數為f(x)=ax-b，三個時刻的擬合函數關系式分別為：f1(x)=28.13x-0.43，f2(x)=23.72x-0.43，f3(x)=18.06x-0.40，符合應力波衰減規律。分析路徑path2情況與此類似。

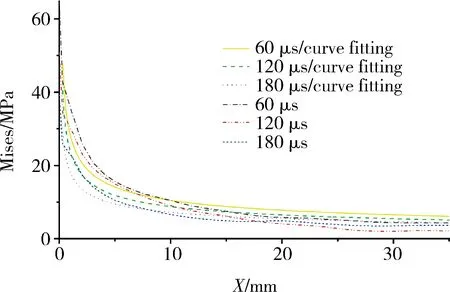
圖4 應力值衰減曲線Fig.4 Curve fitting of stress attenuation

模型A1應力云圖變化如圖5所示。60 μs時結構面兩側以端部為中心，并主要沿下側、外側逐漸擴散，可以觀察到結構面下部區域云圖顏色偏冷色，這說明應力波繞射、透射到此區域較少。120 μs左右，應力云圖持續保持以結構面兩端為中心，主要向下側、外側擴展，向結構面下部中間集中程度并不大，這正是所取分析點Mises應力值震蕩變化的直觀現象，其根本原因是應力波的持續傳播，之所以出現不只一次的峰值，是因為結構面尖端集聚能量釋放的結果，180 μs左右也基本呈現此現象，云圖顏色逐漸轉冷色調。 實際巖體承受強動荷載時，弱面處出現應力集中，集聚較大應變能，并常從此起裂破壞。

圖5 應力云圖變化圖Fig.5 Changing diagram of stress cloud

3.2 結構面長度變化時的動態響應

B組四個模型結構面長度分別為10 mm、20 mm、30 mm、40 mm，截取模型中間部分如圖6所示。

圖6 B組模型示意圖Fig.6 Diagram of group B model

四個分析點B1D、B2D、B3D、B4D的Mises應力值隨時間變化見圖7。分析點B1D和分析點B2D變化規律相似，先震蕩上升，200 μs左右達到峰值，分別為18.02 MPa和16.15 MPa，后者較小，隨后震蕩下降，這是因為隨著結構面長度的增加，應力波較難以繞射到結構面下部區域。同樣，分析點B3D的峰值和整體應力值水平更低。但隨著結構面長度的進一步增加，情況有所不同，模型B4的結構面長度為40 mm，分析點B4D在100 μs左右時達到峰值19.23 MPa，隨后有很短暫的下降后又快速上升，在160 μs左右時再次達到峰值18.86 MPa，隨后震蕩下降。

圖7 下部分析點應力值Fig.7 Stress of down monitoring point

以模型B4為例，在分析路徑path1上，其Mises應力值隨距離衰減曲線如圖8所示。擬合函數為f(x)=ax-b，三個時刻的擬合函數關系式分別為：f1(x)=50.44x-0.59、f2(x)=42.47x-0.60、f3(x)=46.88x-0.60，符合應力波衰減規律。分析路徑path2情況與此類似。

圖8 應力值衰減曲線Fig.8 Curve fitting of stress attenuation

Mises應力云圖變化如圖9所示，90 μs左右，結構面下部開始出現“水滴”狀顏色轉暖色區域，隨后快速消失，在150 μs左右時再次出現此區域；同時可以觀察到結構面側面和下側面接觸，這說明結構面的應變積累，結構面的豎向位移值超過了結構面厚度，相當于節理的等效剛度降低，透射系數增加，在模型建立階段結構面的上下側表面相互作用設置為硬接觸，上表面將應力傳遞到下表面，應力波發生了透射現象。

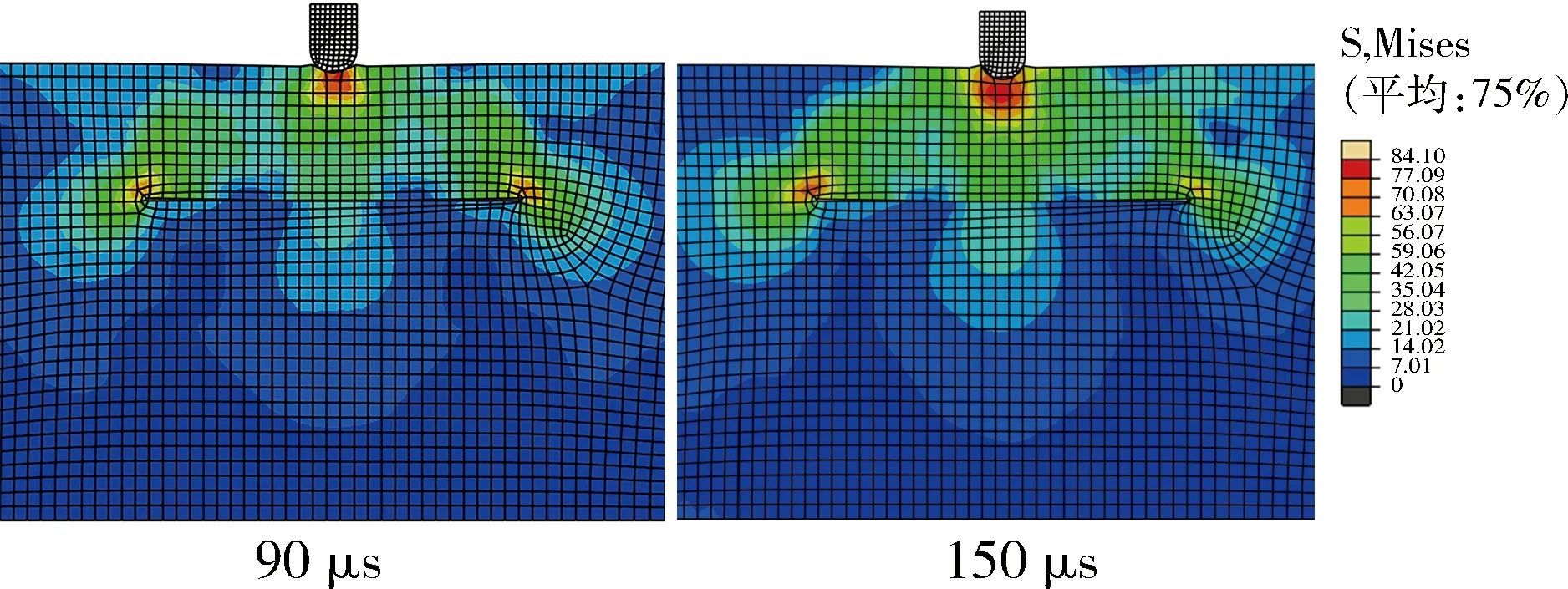
圖9 應力云圖變化圖Fig.9 Changing diagram of stress cloud

3.3 結構面曲率變化時的動態響應

C組模型結構面變化情況如圖10所示。為直觀表示，圖中數值為結構面的曲率半徑大小；由曲率半徑r和曲率k之間的關系式k=1/r可知兩者呈反比，即曲率越來越小，依次為500、333、250、200。

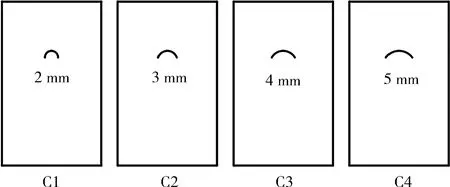
圖10 C組模型示意圖Fig.10 Diagram of group C model

取結構面左側端部四個分析點C1L、C2L、C3L、C4L，其Mises應力值隨時間變化情況如圖11所示。當結構面曲率越來越小時，Mises應力值在60 μs之前的增加速度越來越大，結構面曲率減小，結構面趨于平直，應力波傳播到端部的距離縮短，因此端部的應力值會在較短時間內開始快速增加。分析點C1L在120 μs左右時第一次達到較大值為35.78 MPa，隨后震蕩下降；分析點C2L在60 μs左右時首次達到峰值42.57 MPa，隨后震蕩下降，但隨著結構面曲率的進一步減小；分析點C3L在50 μs左右時便首次出現峰值，大小為42.61 MPa；分析點C4L的峰值出現時間更早，基本上在50 μs左右，這和結構面幾何特征是平直時的端部分析點出Mises應力值峰值出現時間基本一致，這說明隨著曲率減小，結構面趨于平直，其端部Mises應力值在應力波傳播初期有著相似的變化情況。分析點C3L在首次峰值出現后有短暫時間的緩慢下降，趨勢較為平直，這可能是時間間隔不夠短引起的誤差，其下降趨勢應該是震蕩下降，分析點C4L出現不只一次峰值后下降。

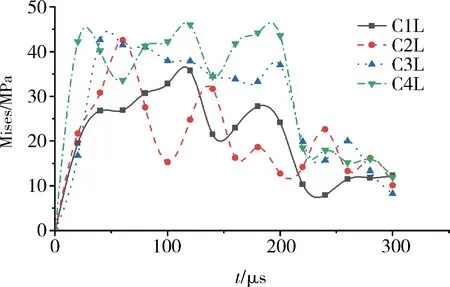
圖11 左側分析點應力值Fig.11 Stress of left monitoring point

應力波在傳播過程中攜帶的能量主要轉化為應變能儲存在介質內部，取分析點處的應變能隨時間變化情況如圖12所示。結構面左側端部的應變能隨時間變化趨勢基本和Mises應力值隨時間變化趨勢保持協調。分析C1L在100 μs左右時應變能積累到最大值，隨后趨于下降；分析點C2L的應變能在60 μs左右時達到峰值，隨后震蕩下降；分析點C3L和C4L的應變能在50 μs左右快速上升到峰值，隨后趨于較平緩下降，在200 μs左右時快速降低；可見隨著結構面曲率的減小，結構面端部積累應變能的情況有所不同，曲率大時，也即結構面越來越“圓”，此時應力波從結構面弧所對應的弦的中垂線方向入射，結構面反射較多的應力波，應力波攜帶的能量也就不容易在此聚集，隨著結構面趨于平直，應力波反射情況趨同于直線型結構面。

圖12 左側分析點應變能Fig.12 Strain energy of left monitoring point

4 結 論

1) 在以結構面端部為起始點豎直向下的分析路徑上，Mises應力值以函數關系式f(x)=ax-b衰減。

2) 結構面厚度增大，應力波難以發生透射，下部分析點應力值水平降低；結構面長度增加，上下表面容易發生閉合現象，應力波發生透射，下部分析點應力值會增大。

3) 結構面曲率減小，即結構面趨于“平直”時，結構面端部應力峰值出現時間早，說明更容易積累應變能；應變能與應力值變化情況保持協調。