基于SWD和MOMEDA的滾動軸承微弱故障特征識別
朱亞軍,胡建欽,李武,林青云,易燦燦
(1.麗水市特種設備檢測院,浙江 麗水 323000;2.武漢科技大學,武漢 430081)
滾動軸承廣泛應用于石油化工、能源、電力、材料冶金等領域,是旋轉機械的重要部件,同時也是易損壞的部件,30%的旋轉機械故障都是由于軸承存在結構損傷所引起[1]。滾動軸承的運行狀態直接影響著整個設備的正常運行,實現對滾動軸承故障的精準診斷具有重要的理論和工程意義。
對滾動軸承微弱故障特征進行增強與提取,是目前的重點研究方向。其中,經驗模態分解(EMD)[2]最先被提出并應用于軸承故障診斷,但其分解所得高頻分量的帶寬較大且頻率分辨率低,在處理頻率成分較為接近的復合故障信號時容易造成模態混疊。而集成經驗模態分解(EEMD)[3]、局部均值分解(LMD)[4]等EMD改進算法仍受到模式混疊、預定義模式數等問題的限制[5],難以在復合故障中準確提取微弱的故障信息。針對軸承復合故障存在的多分量調制和強干擾等特征的問題,文獻[6]提出了群體分解(Swarm Decomposition,SWD)算法,通過對群濾波器參數進行設置以控制分量主模態頻率,使SWD在進行模態分解時能夠將頻率相近的2個諧波信號分離,比EMD改進方法具有更高的頻率區分能力。
最小熵解卷積方法(Minimum Entropy Deconvolution,MED)是一種時域盲卷積技術,已被應用于滾動軸承的故障診斷中[7-8],但其求解出的濾波器并不一定是全局最優濾波器,且往往只能夠提取到少數幾個脈沖成分。針對MED的局限,有學者在相關峭度的基礎上提出了最大相關峭度解卷積方法(Maximum Correlated Kurtosis Deconvolution,MCKD)[9],其相對于MED能夠提取更多的脈沖成分,但也僅能在局部提取有限個脈沖,而且需要依據先驗知識對故障周期、濾波器參數進行設置。因此,文獻[10]提出了多點調整最優最小熵解卷積(Multipoint Optimal Minimum Entropy Deconvolution Adjusted,MOMEDA)方法,利用一個目標向量對解卷積所得脈沖序列的權重和位置進行定義,不需要通過迭代算法即可得到最優濾波器。然而該方法在每次降噪過程中只能夠提取唯一的周期性沖擊,并且在噪聲較強的情況下容易出現誤診斷現象[11-12]。基于以上方法的不足,利用SWD和MOMEDA方法理論上的優勢,對信號進行SWD處理并利用MOMEDA對分解后的有用模態分量進行特征提取,通過對仿真信號及滾動軸承故障試驗臺信號的分析,驗證該方法對滾動軸承故障特征的提取效果。
1 理論描述
1.1 SWD算法
SWD是一種智能的模態分解算法,通過迭代群濾波器將多分量信號分解為多個本征模態函數分量(Intrinsic Mode Function,IMF)之和,SWD的過程為:
(1)
式中:Sy(w)為信號的韋爾奇功率譜[13];q為SWD過程中頻率w作為中心頻率的次數;Ph為閾值。
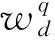
(2)
式中:odd為舍入運算。
2)對信號y(t)進行濾波,得到輸出信號u(t),則輸入輸出信號的方差為
(3)
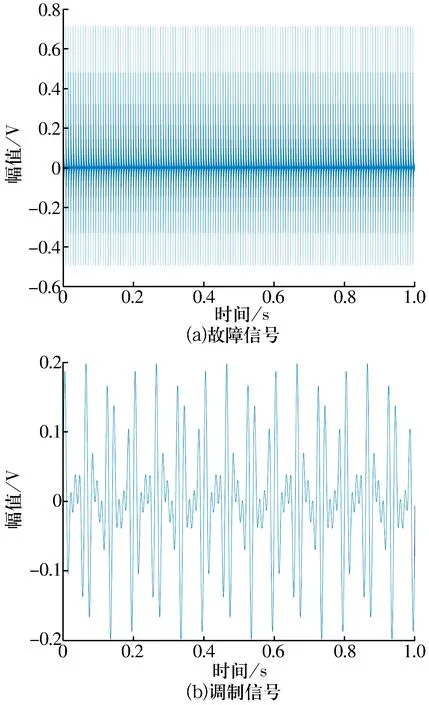
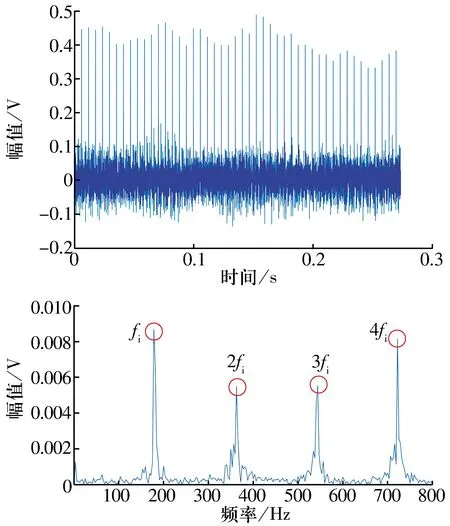
若方差D大于方差閾值Dh,以u(t)為輸入信號重復濾波,直到D 3)更新輸入信號,即 y0(t)=y(t)-Cw(t), (4) Cw(t)=yi(t-τd), 式中:R(x,xi)(τ)為互相關函數;τ為時延。 4)利用更新的輸入信號,重復步驟1—3,直到Sy(w)≤Ph,此時的輸入信號為余量r(t)。 5)計算本征模態函數分量,即 (5) Ωd={w:w=wd}, 式中:k為本征模態函數分量的個數。 MOMEDA方法的目的是尋找一個最佳FIR濾波器系數f(l),使得經過MOMEDA增強后輸出信號的目標函數達到最大。對于輸入的振動信號向量y(t),其目標函數可描述為 (6) 式中:f為濾波器向量;t為確定脈沖權重及位置的目標向量。 對f求導可得 (7) 式中:N為采樣點總數;L為濾波器長度。 將(7)式轉化為矩陣形式,并進一步簡化得 y-1X0t-y-3tTyX0y=0, (8) 式中:X0為脈沖信號的矩陣形式。 (9) 由上式可求出f,即所尋求的最佳濾波器系數。 綜上分析,所設計的滾動軸承故障診斷算法流程如圖1所示:首先對振動信號進行SWD處理,然后選擇有用的本征模態函數分量,最后采用MOMEDA對各分量進行增強和特征提取。 圖1 本文提出方法的流程圖Fig.1 Flow chart of method proposed in this article 滾動軸承故障的模擬信號模型有很多種,最典型的是Randall提出的模型[14-15],為了不失一般性,數值模擬信號表示為 x(t)=x1(t)+x2(t)+n(t), (10) e-B(t-iT-τi)cos(2πfn(t-iT-τi)+φw), x2(t)=0.8×[0.3+0.5cos(2πf1t)]· sin(2πf2), 式中:x1(t)為軸承外圈故障模擬信號;x2(t)為調制信號;n(t)為方差0.5的高斯白噪聲;A0為諧振強度,取1.2;fm為調制頻率(外圈故障時取0);φA,φw和CA均為任意常數;B為衰減系數;T為故障沖擊發生的周期,取0.007 s;τi為第i次沖擊相對于周期T的微小波動;fn為系統的共振頻率;x2(t)中的f1,f2分別取15,50 Hz。 轉頻fr為20 Hz,采樣頻率fs為10 000 Hz,采樣點數N為10 000,外圈故障頻率fe為140 Hz時,軸承故障模擬信號x1(t)和調制信號x2(t)的時域波形如圖2所示,為驗證SWD對多組分復雜 圖2 仿真信號組成分量的時域波形Fig.2 Time domain waveform of components of simulated signal 信號分解的效果,添加了強背景噪聲n(t),含噪信號的時域、頻域波形如圖3所示,由于多組分信號和強噪聲的干擾,從頻譜分析結果中無法正確地識別外圈故障特征和調制特征。 圖3 含噪信號的時、頻域波形Fig.3 Time domain and frequency domain waveforms of noisy signals 利用SWD對多組分仿真信號進行模態分解,一共獲得了6個模態分量,如圖4所示。各模態分量的快速傅里葉變換結果如圖5所示,由圖可知: 圖4 SWD分解后的模態分量Fig.4 Results of mode components after SWD decomposition 圖5 SWD分解后模態分量的頻譜圖Fig.5 Frequency domain of mode components after SWD decomposition IMF3的頻譜對應于調制信號,從圖中可以發現中心頻率f2及調制現象(f2+f1與f2-f1)。 各IMF分量與原始信號x(t)的相關系數見表1,由表可知IMF1與原始信號x(t)的相關系數最大,利用MOMEDA對其進行信號質量增強和降噪,結果如圖6所示,進一步進行頻譜分析所得結果如圖7所示。由圖7可知:從頻譜圖中可以清楚地識別出外圈故障特征頻率fe及其倍頻2fe,3fe,說明本文提出的方法對于多組分信號的降噪和外圈故障特征提取具有明顯的效果。 表1 各IMF分量與原始信號的相關系數Tab.1 Correlation coefficients of each IMF component and original signal 圖6 IMF1分量MOMEDA降噪后的結果Fig.6 Results of IMF1 after MOMEDA denoising 圖7 故障特征頻率的提取結果Fig.7 Result of fault feature frequency extraction 試驗數據來自于西安交通大學提供的滾動軸承全壽命周期數據集[16],該數據集不對軸承預制任何故障,即所使用軸承為全新的軸承,試驗時將其安裝在試驗臺上運行,直至完全失效,數據集由491個數據組成,歷時491 min。 為模擬弱故障的情況,選取內圈故障軸承早期的第30個數據進行分析。故障軸承型號為LDK UER204,鋼球個數為8,外徑為39.8 mm,內徑為29.3 mm,接觸角為0°。利用2個互成 90°角放置于軸承座上的PCB加速度傳感器(型號為352C33)采集軸承的振動數據,采樣頻率fs為25.6 kHz,轉頻fr為37.5 Hz。根據軸承結構參數和轉頻計算可得內圈故障頻率fi為180 Hz。 首先,對實測振動信號進行時域分析和快速傅里葉變換,結果如圖8所示,由圖可知:實測信號的時域波形中含有一些沖擊特征和噪聲干擾;頻譜分析結果中可以識別出轉頻fr及其2倍頻,而另外2個明顯的峰值頻率(232,442 Hz)則與故障特征頻率無關。 圖8 故障軸承實測振動信號的時域圖和頻譜圖Fig.8 Time domain and frequency domain of measured vibration signal for fault bearing 同樣,采用軸承故障診斷常用的包絡譜分析、小波降噪、EEMD等方法對試驗信號進行分析,結果如圖9所示,由圖可知:從包絡譜中無法識別故障特征頻率;小波分析結果中僅可以識別出轉頻及其2倍頻,以及與故障特征無關的峰值頻率232 Hz;EEMD各分量的頻譜圖中也無法準確識別出內圈故障特征頻率;顯然這些方法在對試驗數據進行特征提取時都具有一定的局限性。 圖9 包絡譜、小波降噪及EEMD的分析結果Fig.9 Analysis results for envelope spectrum, wavelet denoising and EEMD 最后,利用SWD對實測故障軸承的振動信號進行模態分解,一共獲得了6個分量,結果如圖10所示。選擇與原始信號相關性最大的IMF1,利用MOMEDA進行信號質量增強和沖擊特征提取,并進行快速傅里葉變換,結果如圖11所示,由圖可知:MOMEDA處理后的信號中存在明顯的沖擊特征,進行快速傅里葉變換處理后可以清楚地識別出內圈故障頻率的1~4倍頻,可以確定故障類型為內圈故障,與實際情況相符。 圖10 SWD分解的結果Fig.10 SWD decomposition results 圖11 IMF1經MOMEDA降噪后的頻譜分析結果Fig.11 Frequency spectrum analysis results of IMF1 after MOMEDA denoising 針對旋轉機械弱故障特征識別方法的不足,提出了一種基于SWD和MOMEDA的滾動軸承弱故障特征識別方法,采用SWD分解多組分復雜振動信號并利用MOMEDA進行特征提取,其目的在于通過SWD分解獲得有用的信號分量,提高信號的信噪比,去除無關成分的干擾;同時,利用MOMEDA實現對信號的濾波和沖擊特征的準確提取。多組分的數值仿真信號和機械故障公開數據集中內圈故障試驗數據的分析結果表明該方法在滾動軸承故障特征提取中的效果較好。1.2 MOMEDA算法
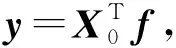
1.3 滾動軸承故障診斷流程
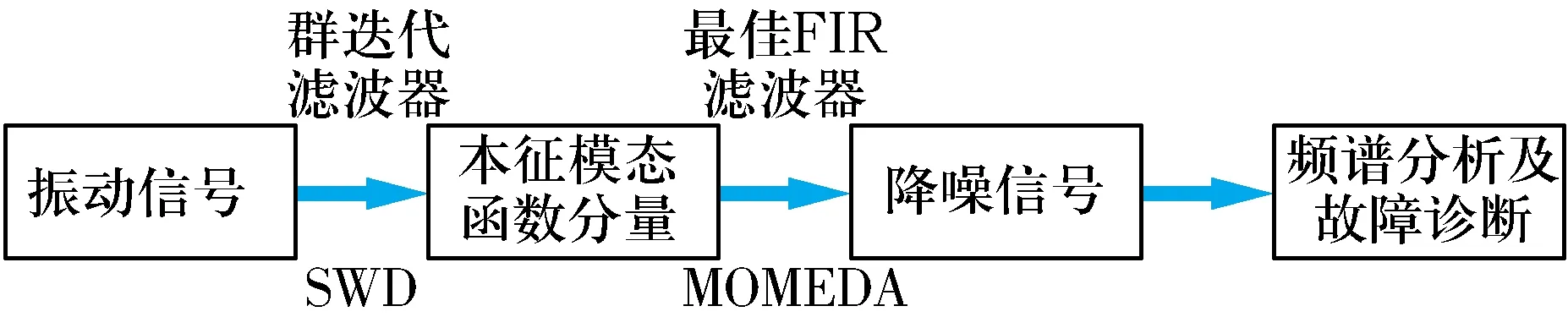
2 數值仿真信號分析
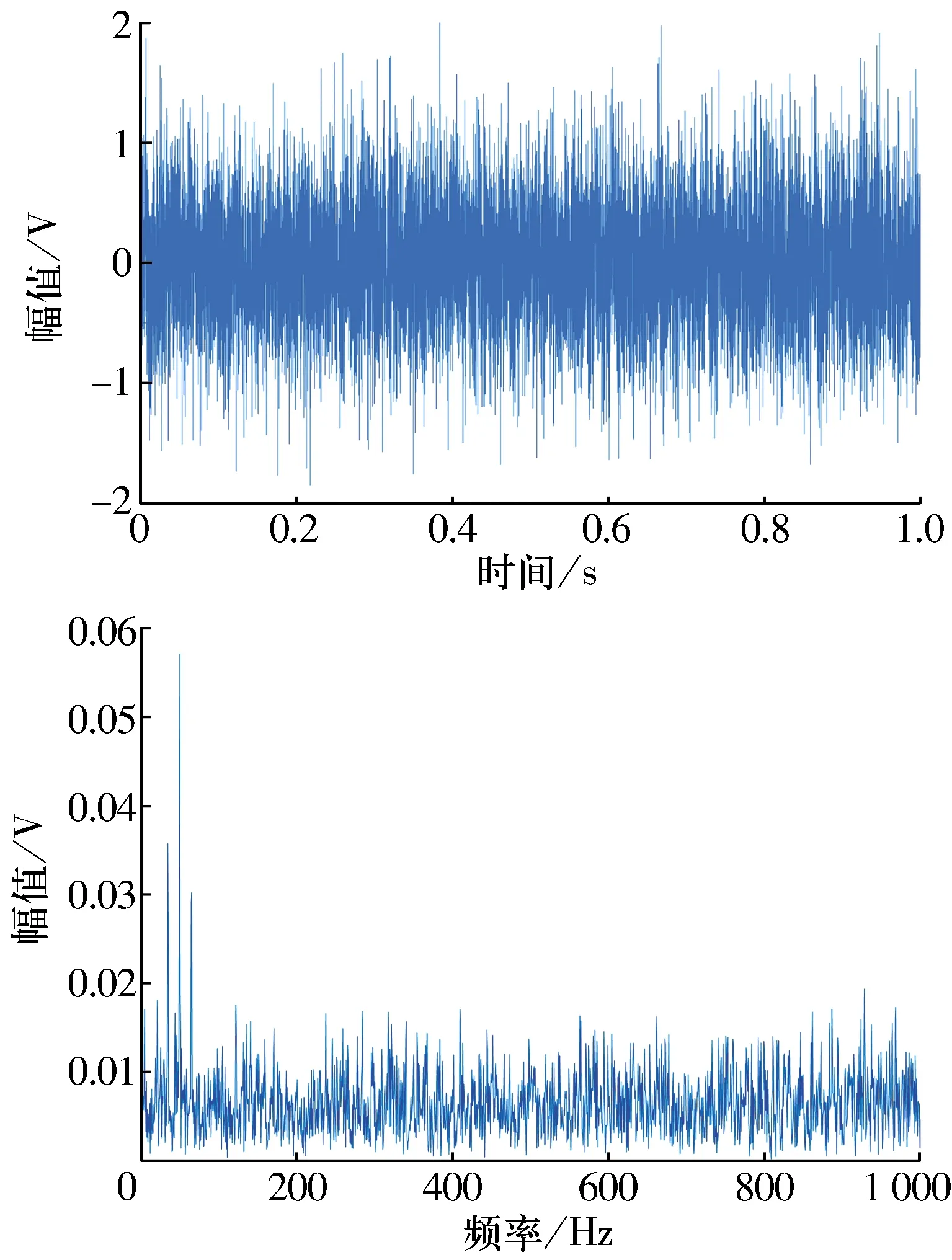
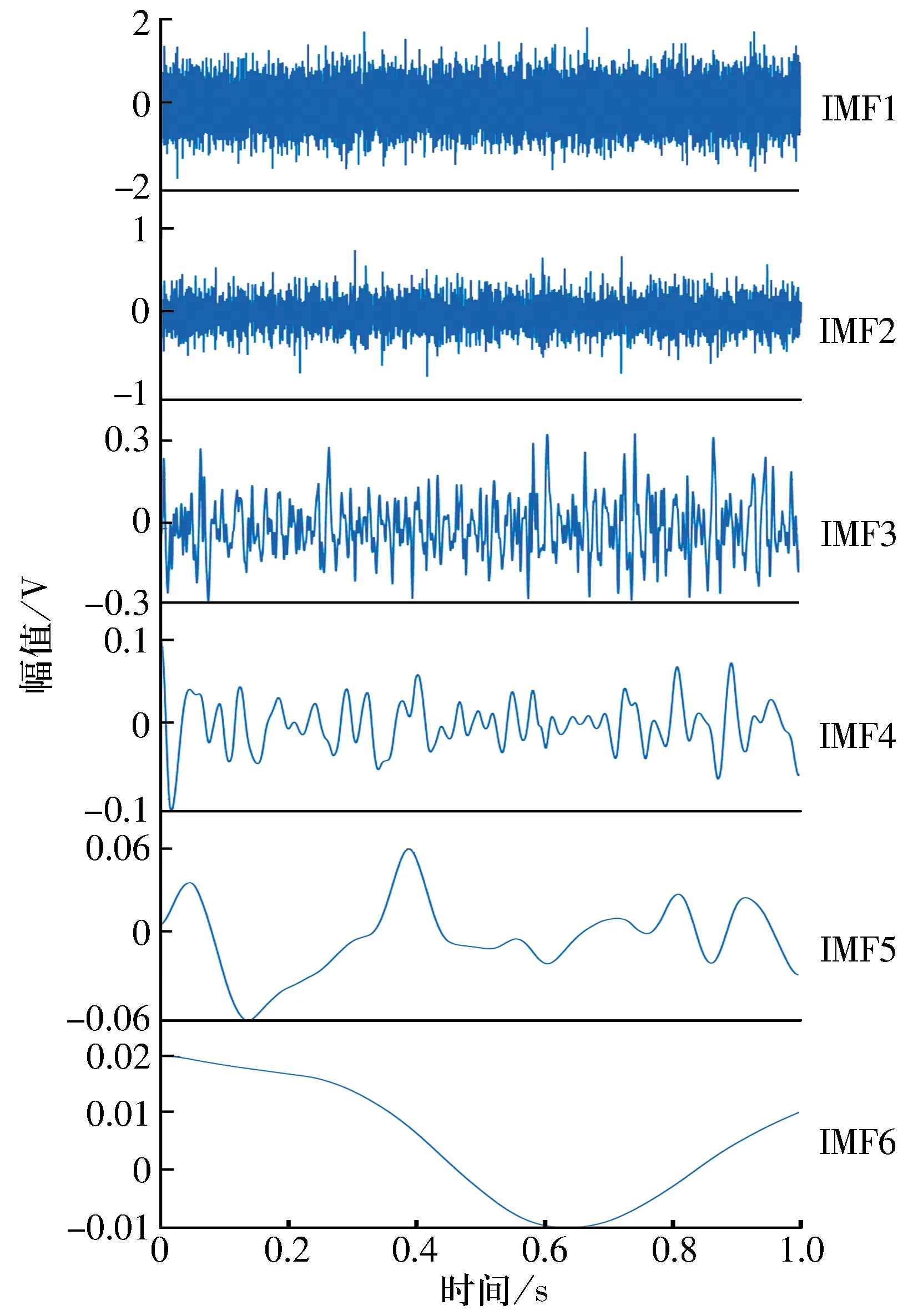
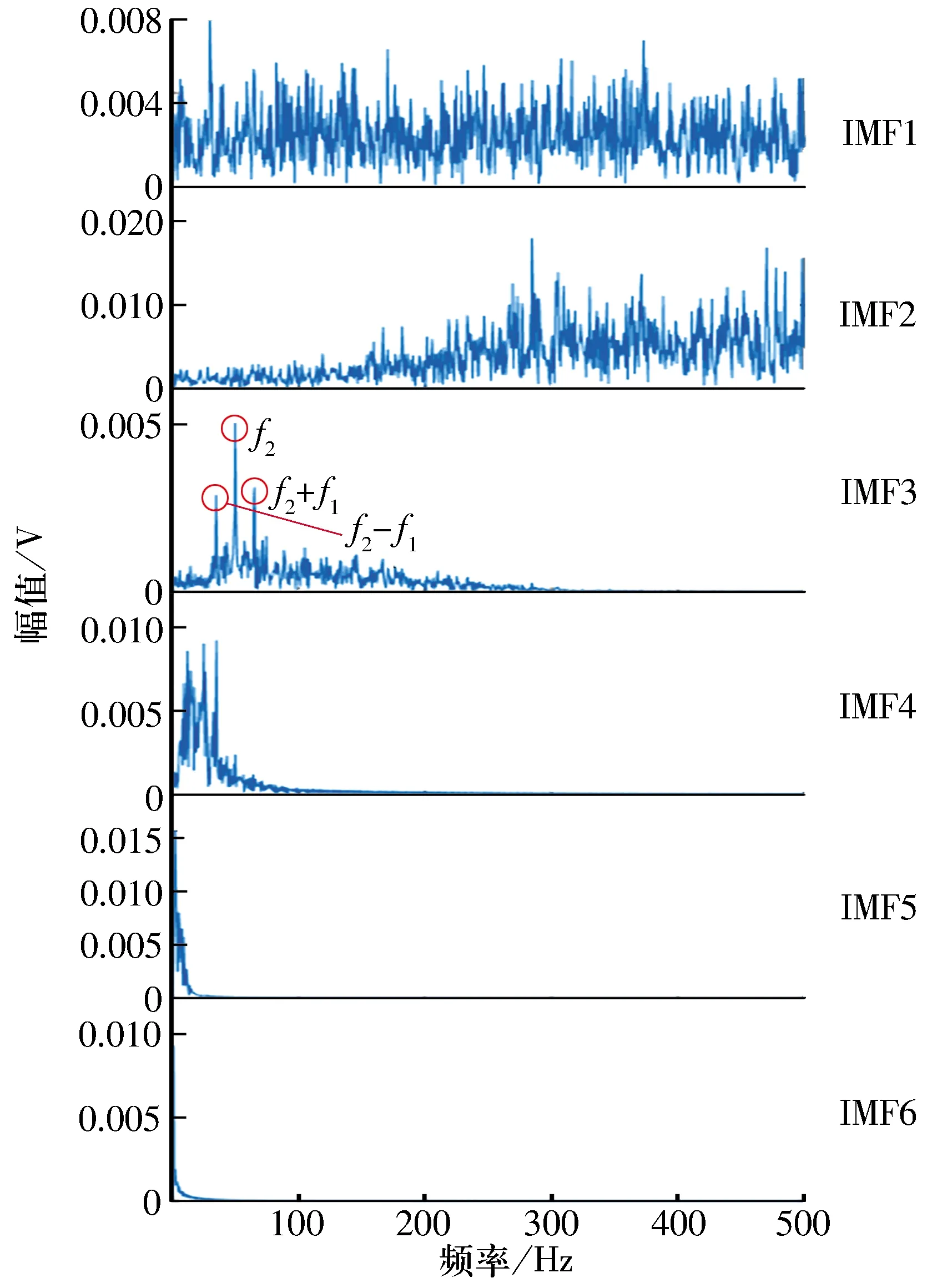

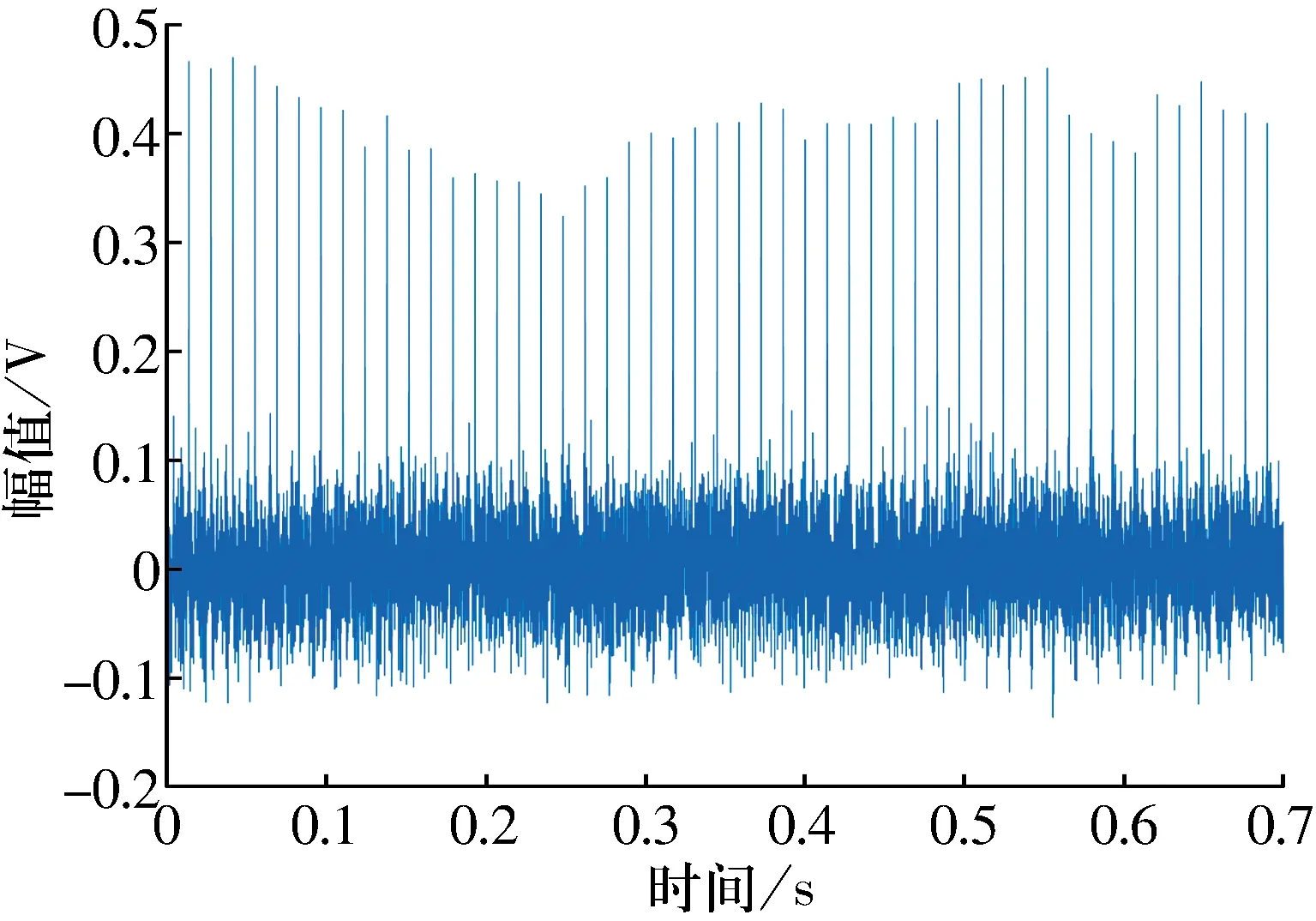
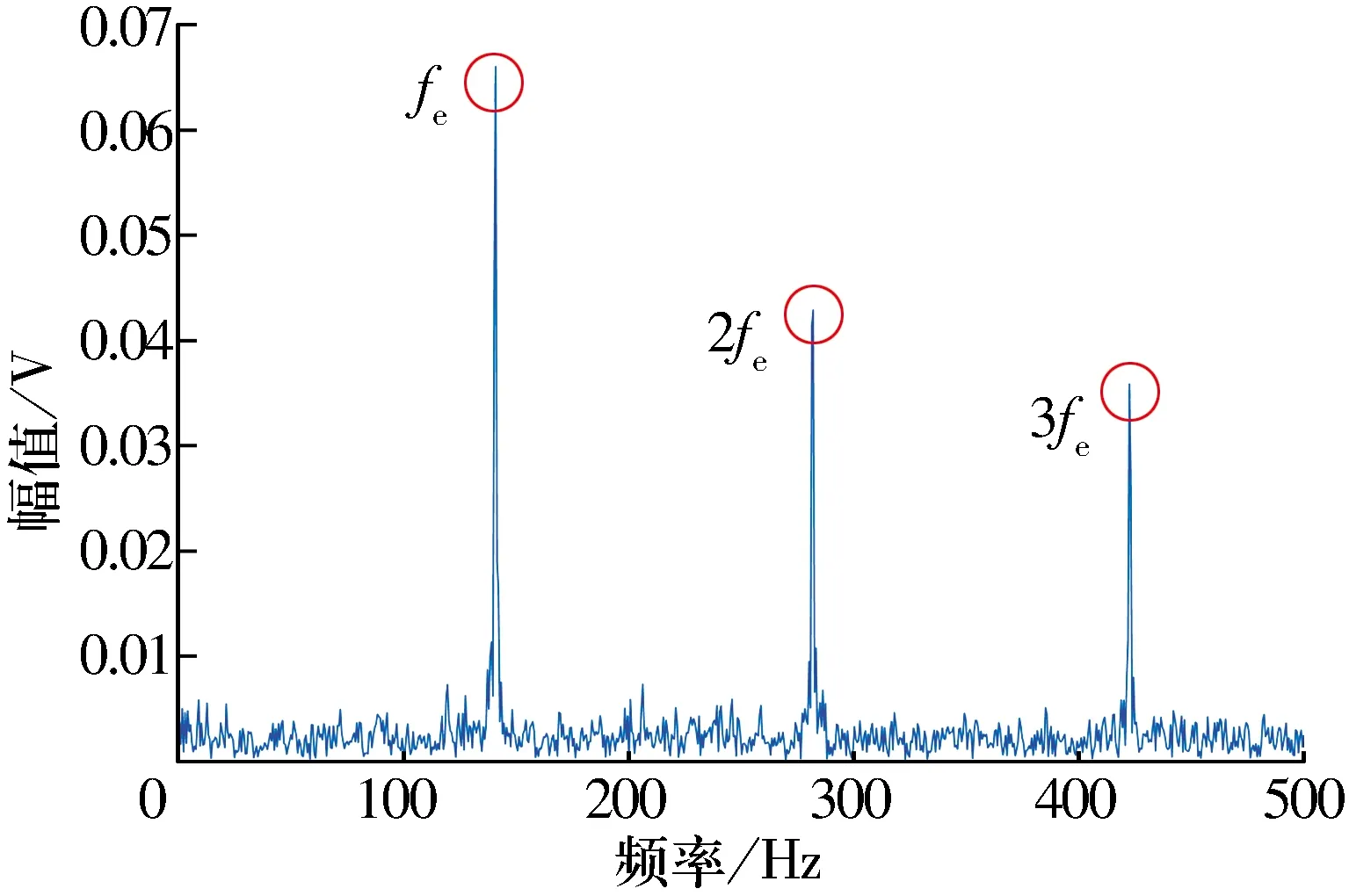
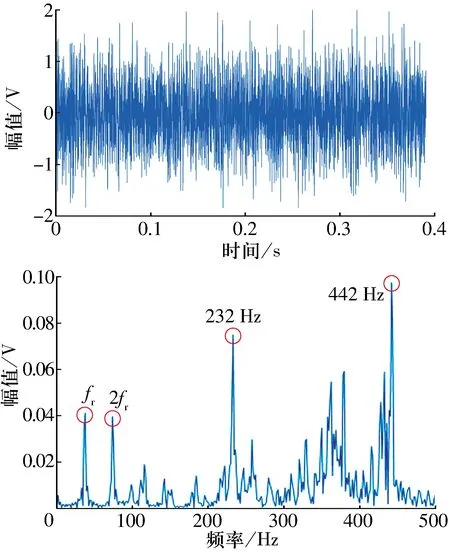
3 試驗數據分析
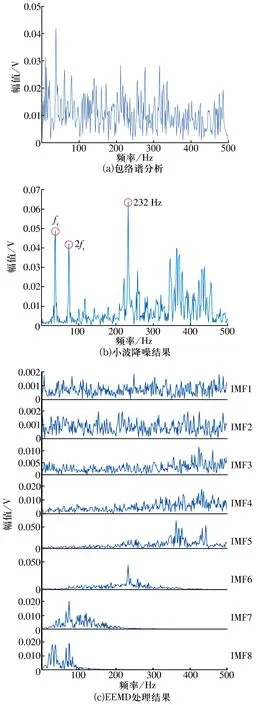
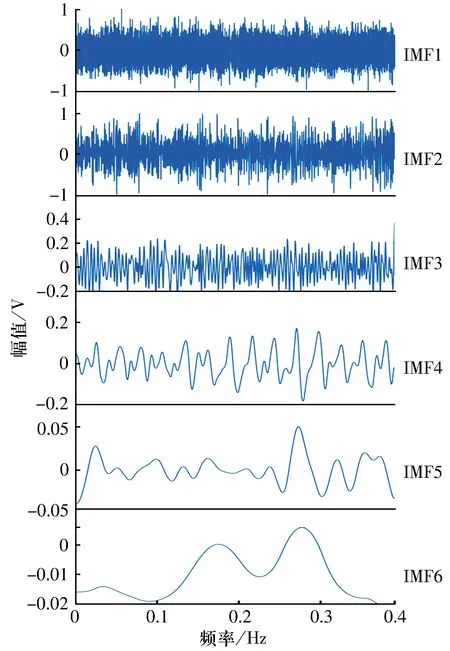
5 結束語

