相關熵的降噪機理及其在軸承故障診斷中的應用

李輝

(天津職業(yè)技術師范大學 機械工程學院，天津 300222)

機電設備故障產生的振動信號具有明顯的非高斯和非線性等特征，相關分析、功率譜估計等基于信號二階統(tǒng)計量的傳統(tǒng)方法在處理這類信號時往往不能取得滿意的效果[1-3]。基于信號高階統(tǒng)計量的雙譜、高階譜分析則在非線性、非高斯信號處理方面有著獨特優(yōu)勢，但高階統(tǒng)計量(Higher Order Statistics，HOS)存在計算方法復雜且計算量大的缺點[4-5]。分數(shù)低階統(tǒng)計量[6-9]( Fractional Lower Order Statistics，F(xiàn)LOS)盡管能在一定程度上消除非高斯噪聲的影響，但卻過度依賴被分析信號噪聲Alpha值的先驗知識，噪聲抑制能力受到極大地限制。相關熵[10-13]是一種分析高斯噪聲和非高斯噪聲的高效方法，已成功應用于通信信號檢測、雷達回波信號檢測、波達方向估計、信號濾波和時延估計等領域，且取得了較好的分析效果[14-19]。雖然相關熵已成功應用于雷達、通信等技術領域，但在機電設備故障診斷領域的應用才剛剛起步，因此，將相關熵與其他信號處理方法相結合，開展基于相關熵技術的機電設備故障特征提取與診斷，具有很重要的理論創(chuàng)新和工程應用價值[20]。

近年來，基于振動信號分析的旋轉機械故障診斷方法在信號降噪、故障特征提取等方面取得了較好的效果，其中的循環(huán)平穩(wěn)分析和譜峭度方法由于其高效性和穩(wěn)健性引起了研究者的矚目[21-22]。但傳統(tǒng)基于信號二階統(tǒng)計量的循環(huán)平穩(wěn)信號分析在處理強高斯噪聲和非高斯噪聲時會造成性能衰退，甚至失效。因此，針對傳統(tǒng)相關函數(shù)和譜相關密度難以有效處理強非高斯噪聲干擾的問題，提出了基于循環(huán)平穩(wěn)相關熵的故障診斷方法，從理論分析、幾何圖解和信號仿真等幾個方面系統(tǒng)闡釋了相關熵的降噪機理，并通過試驗驗證循環(huán)平穩(wěn)相關熵在滾動軸承故障診斷中有效處理染噪信號的能力。

1 相關熵及循環(huán)平穩(wěn)相關熵

1.1 相關熵的估計

對于任意2個實隨機變量x,y，其互相關熵可定義為

Vσ(x,y)=E[κσ(x-y)]，

(1)

式中：κσ(·)為滿足Mercer條件的核函數(shù)；σ為核函數(shù)的核長。σ定義了隨機變量x和y相似性的特征長度尺度，即權重空間視角下特征空間映射前后隨機變量x與y之間距離的比例。

對于實信號x(t)∈R，時變自相關熵可定義為

(2)

κσ(·)一般采用高斯核函數(shù)，其解析式為

κσ[x(t),x(t+τ)]=

(3)

式中：·為一種范數(shù)算子。

在實際應用中，假設x(i)是長度為N的觀測樣本，其自相關熵(下文統(tǒng)稱為相關熵)的無偏估計可表示為

(4)

式中：m為時延的采樣點數(shù)，m=0,1,2,…,N-1。由(4)式估計的相關熵是一個正定的對稱函數(shù)。

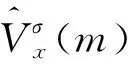
V=

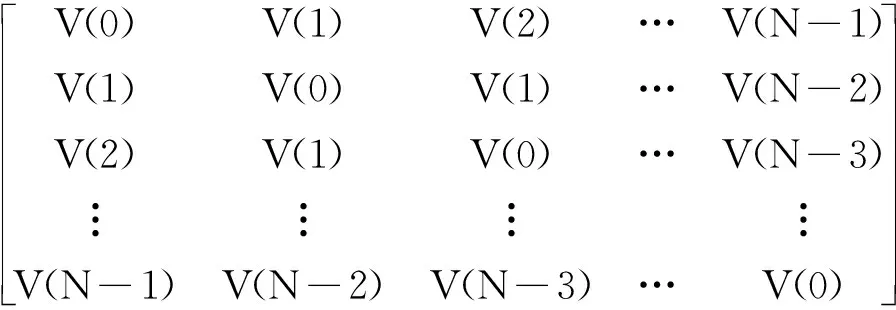
(5)

上述相關熵矩陣V是N×N的正定、對稱矩陣。

1.2 循環(huán)平穩(wěn)相關熵

(6)

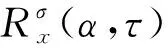
(7)

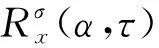
(8)

1.3 循環(huán)平穩(wěn)相關熵譜密度計算步驟

在實際應用中可通過以下步驟計算信號的循環(huán)平穩(wěn)相關熵譜密度：

1)根據(jù)(4)式計算信號的相關熵。

2)根據(jù)(5)式計算信號的相關熵矩陣V。

3)計算相關熵矩陣V各行的傅里葉變換，得到信號循環(huán)平穩(wěn)相關熵函數(shù)矩陣R。

4)計算信號循環(huán)平穩(wěn)相關熵函數(shù)矩陣R各列的傅里葉變換，得到信號的循環(huán)平穩(wěn)相關熵譜密度函數(shù)矩陣S。

2 相關熵的降噪機理

2.1 理論分析

將(2)式表示的時變相關熵展開為泰勒級數(shù)形式，即

x(t+τ)]2n}。

(9)

由(9)式可知：

3)可通過調整σ來控制高斯核函數(shù)曲線的形狀，σ的引入使相關熵函數(shù)和循環(huán)平穩(wěn)相關熵譜密度對于具有不同統(tǒng)計特性(概率密度)的信號都具有適應性，因此，可根據(jù)分析信號的性質和目的選擇合適的σ。

2.2 幾何圖解

不失一般性，假設有2個隨機變量X和Y，則可由(1)式表示的互相關熵定義相關熵誘導的度量[12](Correntropy Induced Metric，CIM)，即

(10)

SCIM(X,Y)是對稱函數(shù)，當核函數(shù)為平移不變核函數(shù)(如高斯核函數(shù))時，SCIM(X,Y)也是平移不變的。SCIM(X,Y)是隨機變量X與Y之間相似性的一種度量，SCIM(X,Y)越大，表示X與Y越不相似，反之，SCIM(X,Y)越小，表示X與Y越相似。為透徹理解SCIM(X,Y)蘊含的內在規(guī)律，繪制了σ=1時SCIM(X,0)的三維圖(圖1)，其等高線圖如圖2所示。

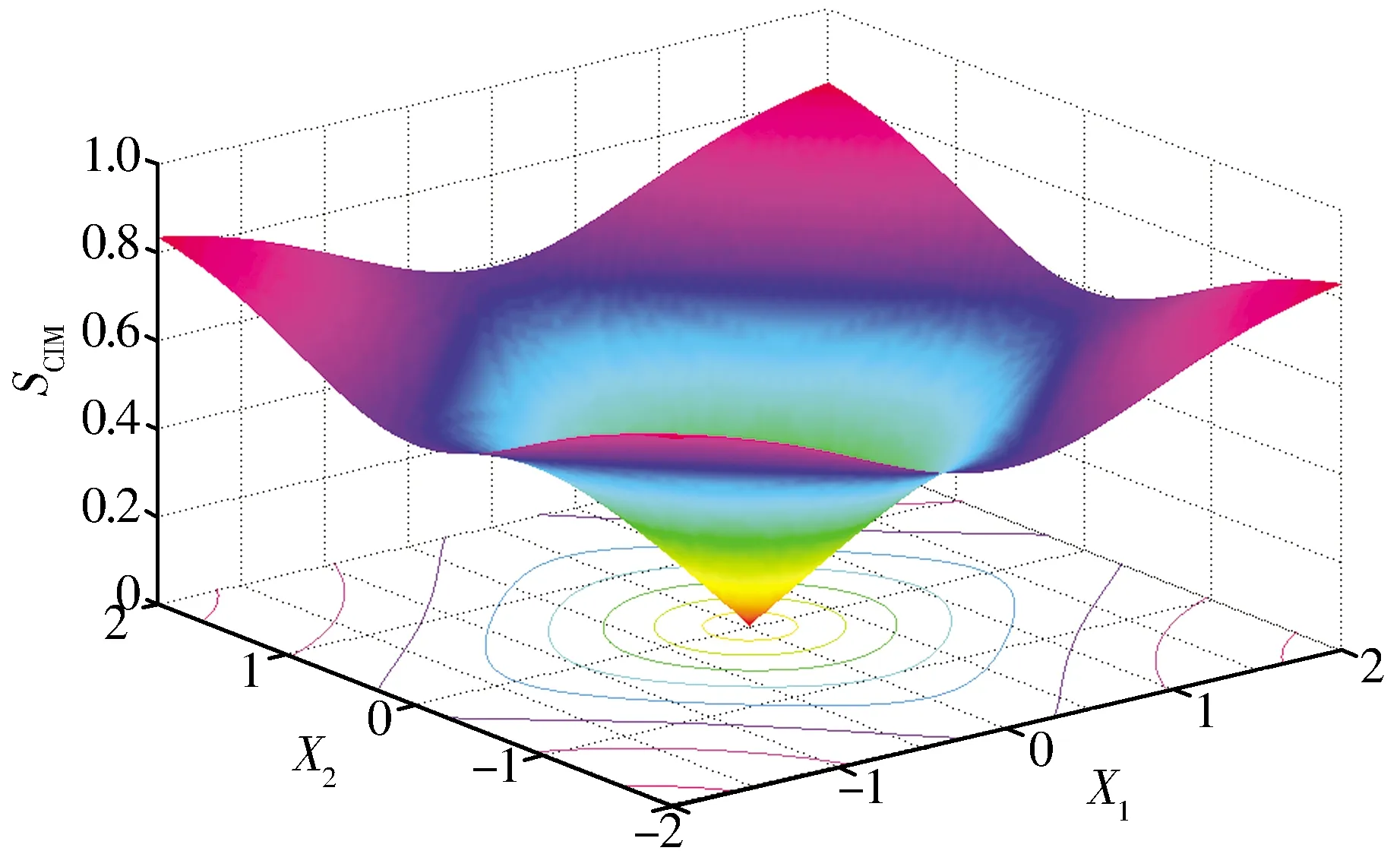
圖1 SCIM(X,0)三維圖(σ=1)Fig.1 3D diagram of SCIM(X,0)(σ=1)

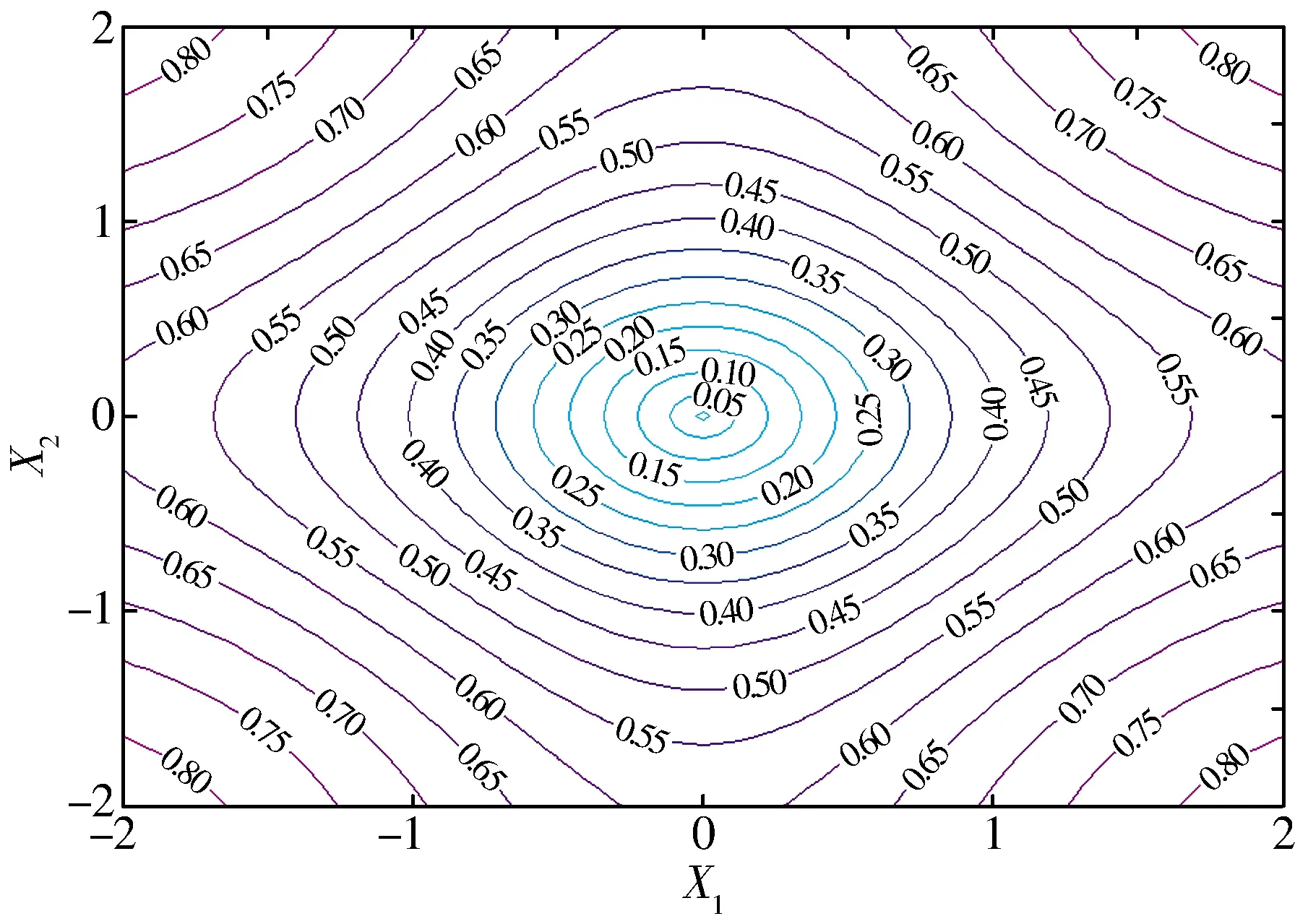
圖2 SCIM(X,0)等高線圖(σ=1)Fig.2 Contour map of SCIM(X,0)(σ=1)

由圖1、圖2可知，不同區(qū)域的SCIM(X,0)具有不同的形狀，根據(jù)SCIM(X,0)的形狀和性質，可以將SCIM(X,0)分為3個區(qū)域：

1)歐幾里得區(qū)，即圖2中心圓形區(qū)域部分。當空間中兩點間距離很近時，SCIM相當于L2范數(shù)。

2)過渡區(qū)，即圖2中近似方形區(qū)域部分。當空間中兩點間距離比較近時，SCIM相當于L1范數(shù)。

3)矯正區(qū)，即圖2中以4個角為中心的扇形區(qū)域部分。當空間中兩點間距離很遠時，SCIM相當于L0范數(shù)，在該區(qū)域，隨著兩點間距離的繼續(xù)增大，SCIM的值將趨于飽和(不變)，因此，該區(qū)域是信號異常值的免疫區(qū)。

綜上可知，SCIM可以作為2個隨機變量相似性的度量工具：SCIM越小，表明2個隨機變量越相似；SCIM=0，2個隨機變量完全相同；SCIM越大，2個隨機變量的差異越大。

當信號中含有幅值較大的異常值時，其SCIM值將位于矯正區(qū)，而矯正區(qū)是信號異常值的免疫區(qū)，SCIM將趨于不變，異常值對SCIM幾乎沒有影響，因此，相關熵能有效抑制信號中的異常值，對于隨機脈沖噪聲具有很強的免疫力，因而基于相關熵的信號分析具有很好的魯棒性。

為對比核長σ對相關熵的影響，繪制了σ=0.1時SCIM(X,0)的三維圖及其等高線圖，結果如圖3、圖4所示。對比圖1—圖4可知：σ越大，歐幾里得區(qū)范圍越大，矯正區(qū)范圍越小；σ越小，歐幾里得區(qū)范圍越小，矯正區(qū)范圍越大；離原點很遠的點，其SCIM表現(xiàn)為各向異性，即距離與方向有關。

圖3 SCIM(X,0)三維圖(σ=0.1)Fig.3 3D diagram of SCIM(X,0)(σ=0.1)

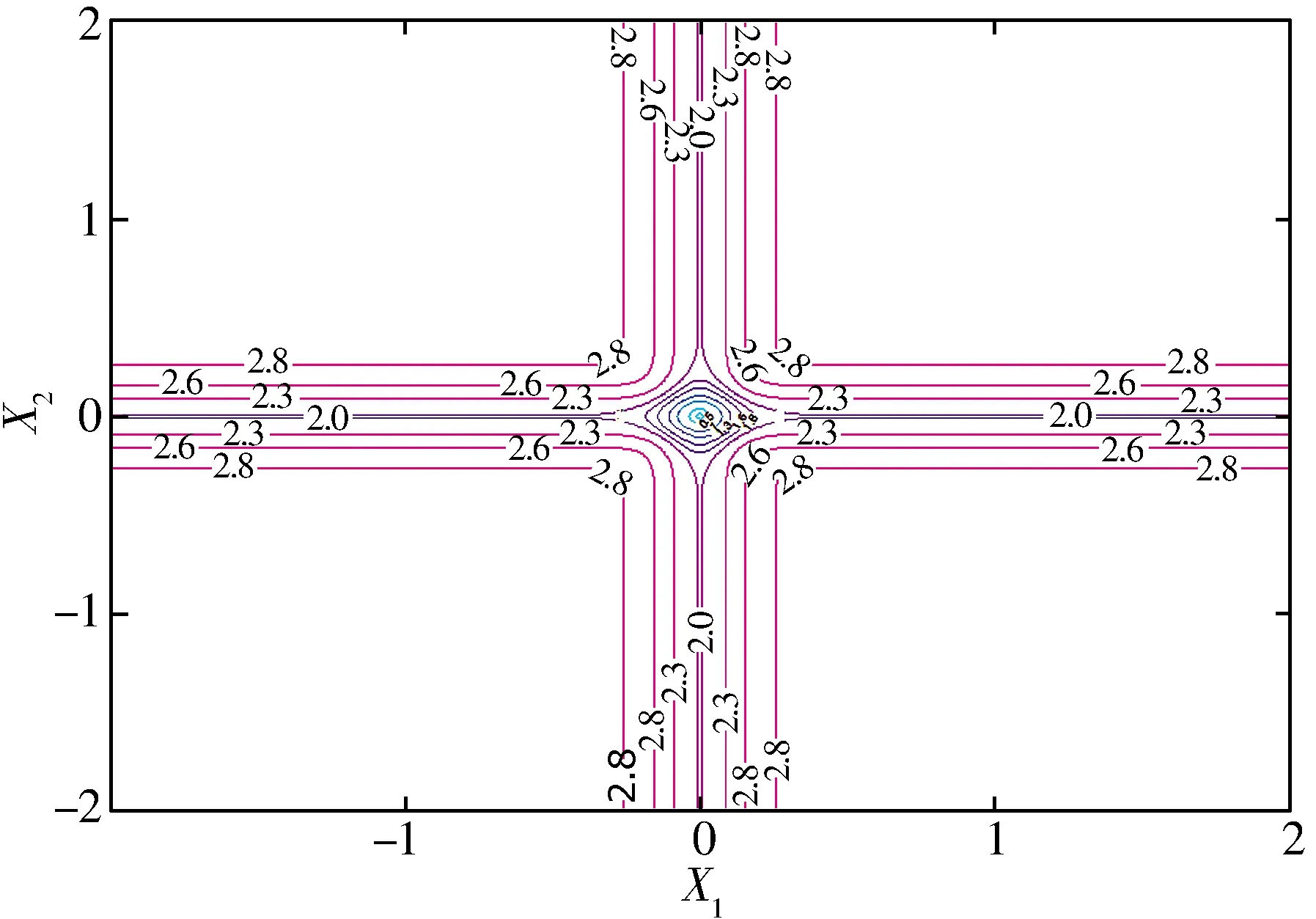
圖4 SCIM(X,0)等高線圖(σ=0.1)Fig.4 Contour map of SCIM(X,0)(σ=0.1)

由此可以看出：核長σ對于空間中兩點間距離的度量具有重大影響，當σ值較大時，歐幾里得區(qū)范圍較大，相當于傳統(tǒng)的二階統(tǒng)計量適用的區(qū)域，可以對線性信號進行有效處理；當σ值較小時，歐幾里得區(qū)范圍較小，矯正區(qū)范圍較大，相當于高階統(tǒng)計量適用的區(qū)域，可以對非線性信號進行有效處理。因此，在實際應用時，可以根據(jù)被處理信號的性質，選擇合適的核長σ。

2.3 小結

通過以上分析可以得出以下結論：

1)相關熵是基于核函數(shù)的隨機變量間局部相似性度量方法，其既考慮了隨機時間信號的統(tǒng)計特性(概率密度)，又考慮了隨機時間信號的時間結構(相關關系)，是傳統(tǒng)相關函數(shù)的一般化和推廣，在包含傳統(tǒng)相關函數(shù)特性的基礎上提高了性能。

2)相關熵不僅包含隨機變量幅值的二階矩，而且包含了隨機變量幅值的高階矩，因此能夠有效刻畫信號的非線性特征，有效處理非線性信號。

3)相關熵能夠有效抑制高斯及非高斯噪聲，基于核函數(shù)的相關熵為高斯、非高斯噪聲的處理提供了一種嶄新的魯棒性解決方法。

4)相關熵利用核函數(shù)，將原特征空間線性不可分的數(shù)據(jù)映射到高維希爾伯特空間，將其轉變?yōu)榫€性可分的數(shù)據(jù)，從而能有效刻畫原特征空間數(shù)據(jù)的非線性特征。

5)相關熵利用核函數(shù)，能高效進行內積運算，節(jié)省了計算時間。

3 仿真驗證

3.1 相關熵核長的影響

由高斯核函數(shù)定義的相關熵有一個自由核長參數(shù)σ，用一個余弦信號說明核長σ對相關熵的影響，并驗證相關熵抑制非高斯噪聲的能力。余弦信號的頻率為10 Hz，采樣頻率為1 000 Hz，采樣時間為1 s，余弦信號及其傅里葉變換如圖5所示。

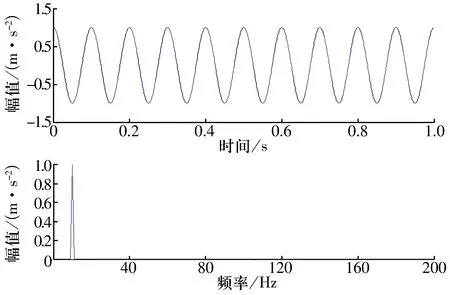
圖5 仿真余弦信號及傅里葉變換Fig.5 Simulative cosine signal and its FFT

當σ取0.04，0.40，1，10時，根據(jù)(4)式計算余弦信號的相關熵及其頻譜，結果如圖6、圖7所示，由圖可知：隨著σ的增大，相關熵會逐漸接近于傳統(tǒng)的自相關函數(shù)；當σ減小時，相關熵趨向于正值，相關熵與相關函數(shù)的時域波形則完全不同；當σ趨近于0時，相關熵趨近于脈沖信號。σ的取值越小，相關熵的頻譜圖中包含信號頻率的高次諧波成分越多，隨著σ的增大，相關熵的頻譜圖中包含信號頻率的高次諧波成分越少，例如當σ=10時，相關熵的頻譜圖與余弦信號的頻譜圖相同。綜上可知，核長σ是影響相關熵中統(tǒng)計量成分的權重系數(shù)，與根據(jù)相關熵的泰勒展開式的理論分析相吻合，其主要原因是高斯核函數(shù)是一種非線性變換，因此，在信號處理時應根據(jù)信號的性質選取適當?shù)暮碎L。

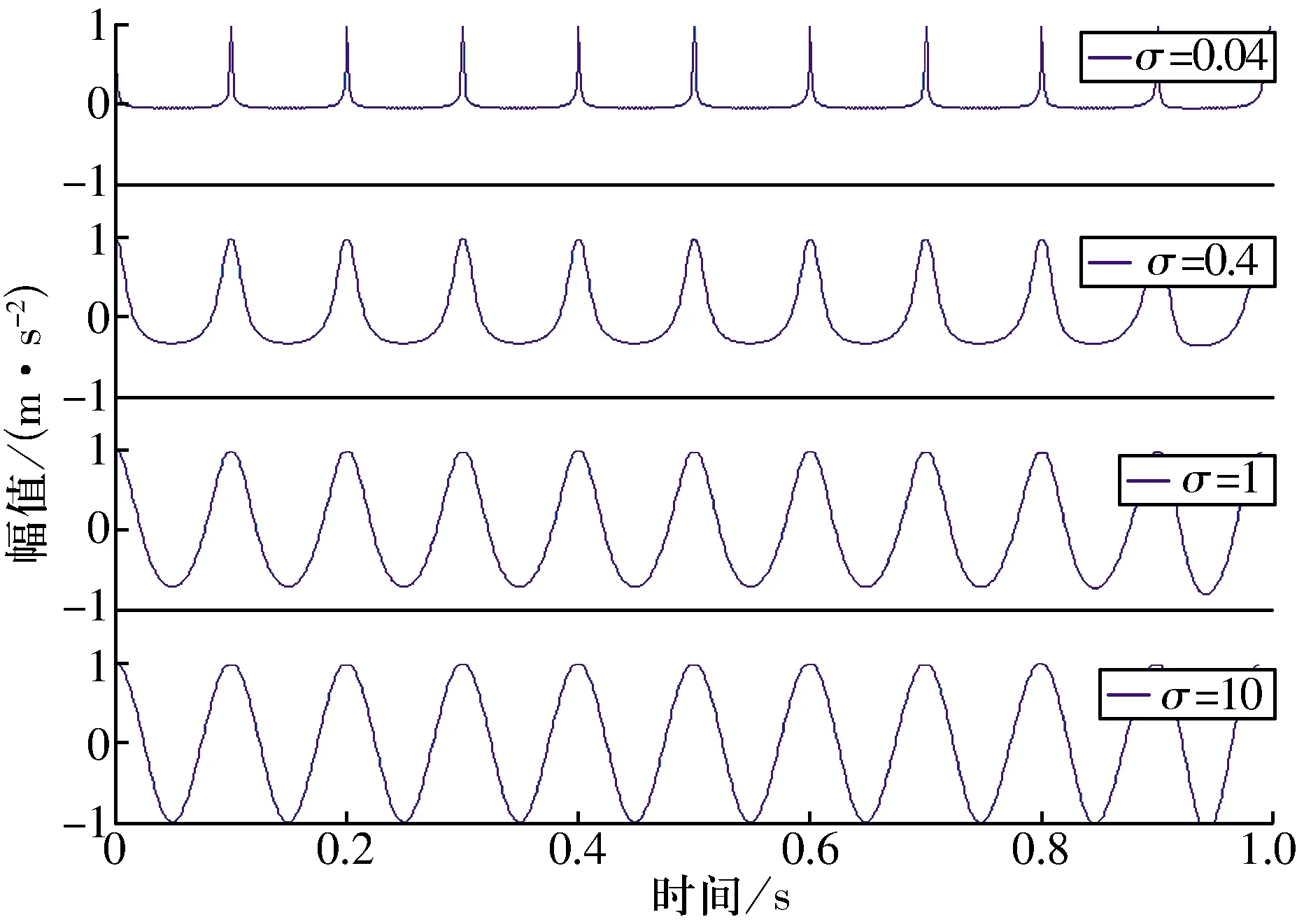
圖6 余弦信號的相關熵Fig.6 Correntropy for cosine signal

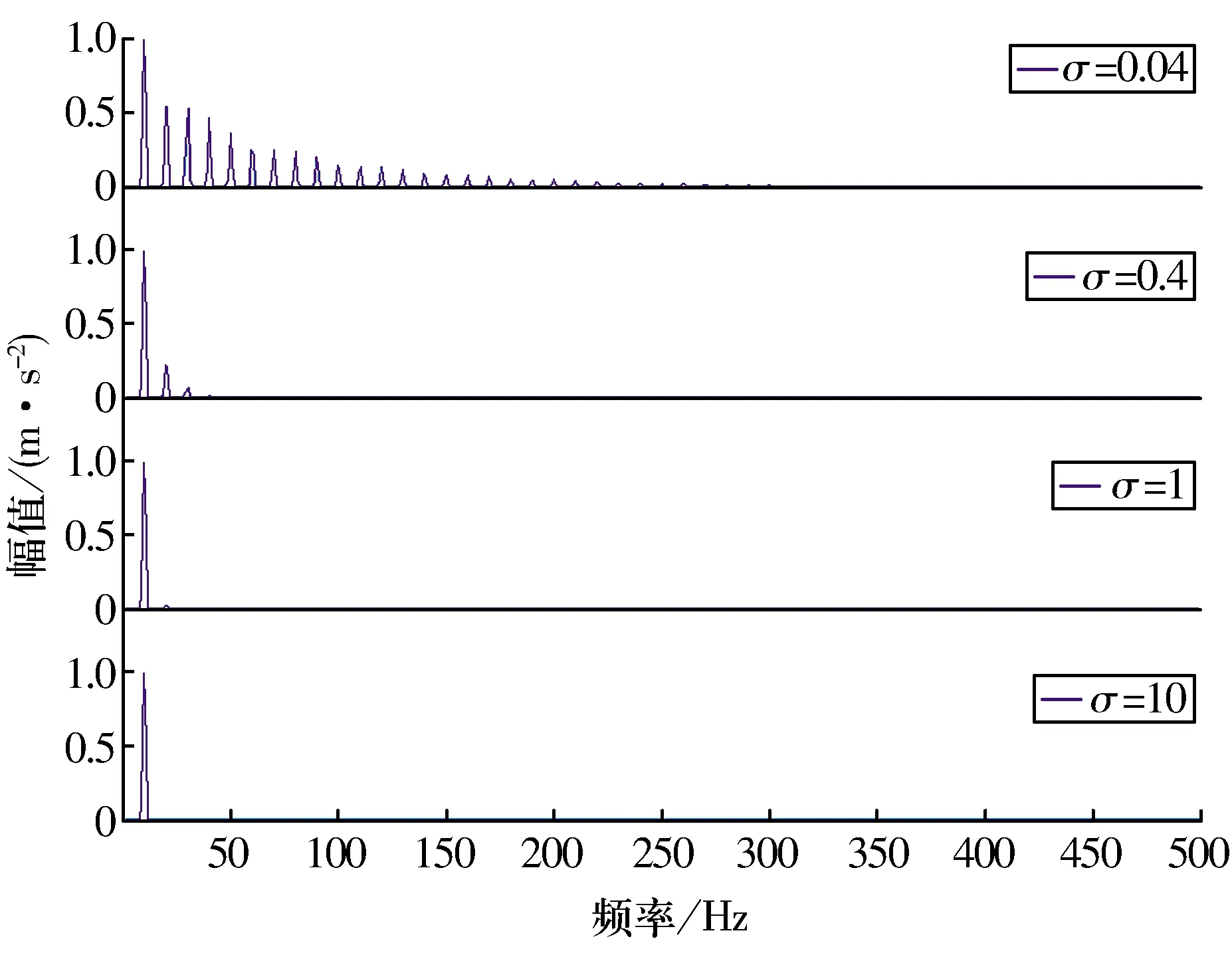
圖7 余弦信號相關熵的傅里葉變換Fig.7 FFT of correntropy for cosine signal

為對比相關熵與傳統(tǒng)相關函數(shù)處理非高斯噪聲的性能，將Alpha分布噪聲(圖8a)與余弦信號進行合成，合成信號如圖8b所示，其廣義信噪比為-10 dB。由于強非高斯噪聲的影響，從合成信號的傅里葉變換結果(圖8c)中無法識別出余弦信號的頻率成分。

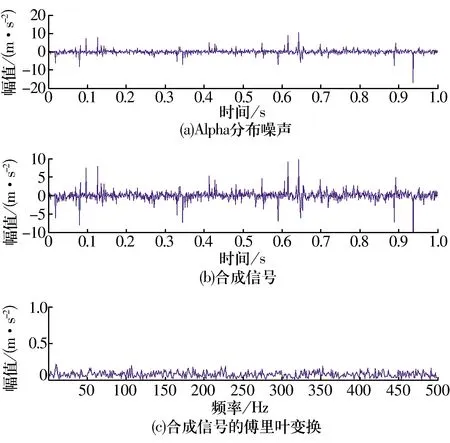
圖8 余弦信號與Alpha分布噪聲合成信號及其傅里葉變換Fig.8 Composite signal of cosine signal with Alpha noise and its FFT

合成信號的自相關函數(shù)如圖9所示，由圖可知：自相關函數(shù)在τ=0時取得最大值，但從圖中無法觀察到合成信號中的周期性變化；而由于Alpha分布噪聲的二階統(tǒng)計量不存在，從自相關函數(shù)的傅里葉變換圖中也無法識別余弦信號的頻率成分；因此，傳統(tǒng)基于二階統(tǒng)計量的信號處理方法，在處理含有非高斯噪聲的信號時，會造成性能衰退，甚至失效。

圖9 合成信號的相關函數(shù)及其傅里葉變換Fig.9 Correlation function and FFT of composite signal

為有效識別合成信號中的頻譜成分，對合成信號進行相關熵運算(σ=0.4)，結果如圖10所示，由圖可知：相關熵圖中可以觀察到明顯的周期性變化，而相關熵的傅里葉變換圖中存在顯著的譜峰(10 Hz處)，表明相關熵能從強非高斯噪聲中提取信號的周期成分。

圖10 合成信號的相關熵及其傅里葉變換Fig.10 Correntropy and FFT of composite signal

3.2 循環(huán)平穩(wěn)相關熵降噪性能仿真

采用一個仿真調幅信號詳細解釋循環(huán)平穩(wěn)相關熵的降噪機理，并驗證其有效抑制噪聲的能力，仿真調幅信號的解析表達式為

x(t)=[1+cos(2πf0t)]cos(2πfct)+

n1(t)+n2(t)，

(11)

式中：f0為調制頻率，取200 Hz；fc為載波頻率，取1 000 Hz；n1(t)為零均值高斯白噪聲；n2(t)為隨機脈沖噪聲。信號的采樣頻率為6 000 Hz，采樣點數(shù)為600，通過該仿真調幅信號，利用循環(huán)平穩(wěn)相關熵譜密度詮釋循環(huán)平穩(wěn)相關熵的降噪機理并驗證其對高斯白噪聲和隨機脈沖噪聲的降噪性能。

在仿真調幅信號x(t)中加入零均值高斯白噪聲n1(t)，獲得信噪比為-10 dB的合成信號，之后再隨機加入幾個幅值不等的脈沖信號以模擬隨機脈沖噪聲。仿真調幅信號的時域波形如圖11所示，由于調幅信號完全被噪聲淹沒，從時域波形中已完全看不出信號的變化規(guī)律，在其傅里葉變換圖中也很難識別載波頻率及調制頻率。

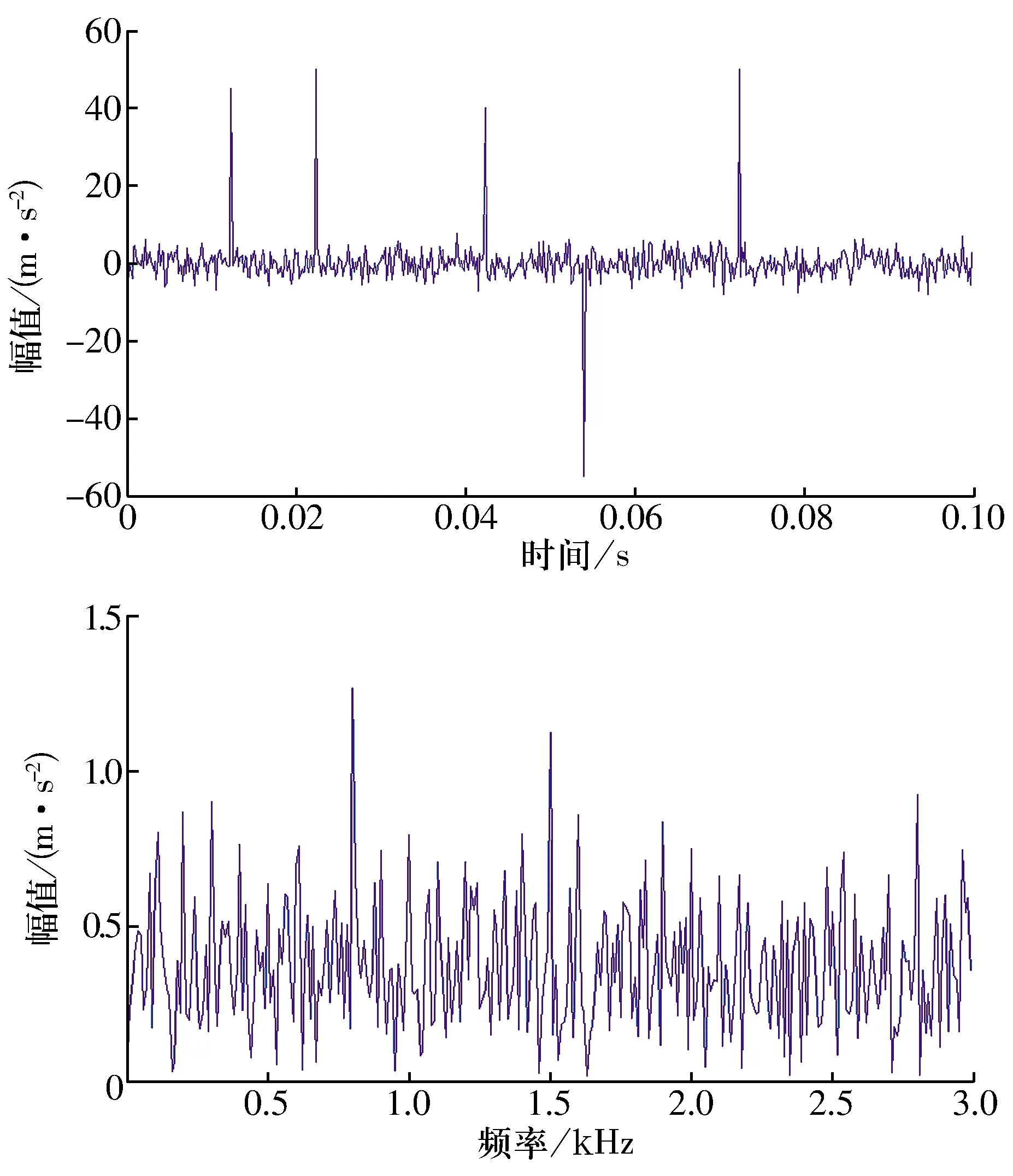
圖11 仿真調幅信號的時頻圖Fig.11 Time-frequency diagram of simulative amplitude modulation signal

計算仿真調幅信號的循環(huán)平穩(wěn)相關熵譜密度(σ=3)，結果如圖12所示，由圖可知：在循環(huán)頻率α和譜頻率f構成的雙頻平面內，信號的能量主要分布在f=0,α=0及f=-0.5α這3條頻譜線上，其余區(qū)域循環(huán)平穩(wěn)相關熵譜密度的能量為零，表明循環(huán)平穩(wěn)相關熵譜具有很強的能量聚集性，其中高斯噪聲的能量主要聚集在f=0及α=0這2條頻譜線上；調幅信號的能量主要聚集在f=-0.5α這條頻譜線上；非高斯噪聲能量分散在其他區(qū)域，已被循環(huán)平穩(wěn)相關熵譜有效抑制。

圖12 仿真調幅信號循環(huán)平穩(wěn)相關熵譜Fig.12 Cyclostationary correntropy spectrum of simulative amplitude modulation signal

在低頻段，仿真調幅信號x(t)的循環(huán)平穩(wěn)相關熵譜在α=±f0的位置存在明顯的譜峰，對應信號的調制頻率f0，表明能準確識別調制頻率f0；在高頻段，α=±2fc±f0及α=±4fc位置存在明顯譜峰，表明能準確識別載波頻率fc和調制頻率f0。

根據(jù) (8) 式計算循環(huán)平穩(wěn)相關熵輪廓，結果如圖13所示，圖中的α=±f0，α=±2fc±f0及α=±4fc位置存在明顯的譜峰。由于相關熵能有效抑制高斯噪聲和脈沖噪聲，因此循環(huán)平穩(wěn)相關熵譜具有很強的從強高斯噪聲和非高斯噪聲中提取信號特征的能力，基于高斯核函數(shù)的循環(huán)平穩(wěn)相關熵為高斯、非高斯噪聲的處理提供了一種嶄新的有效處理方法。

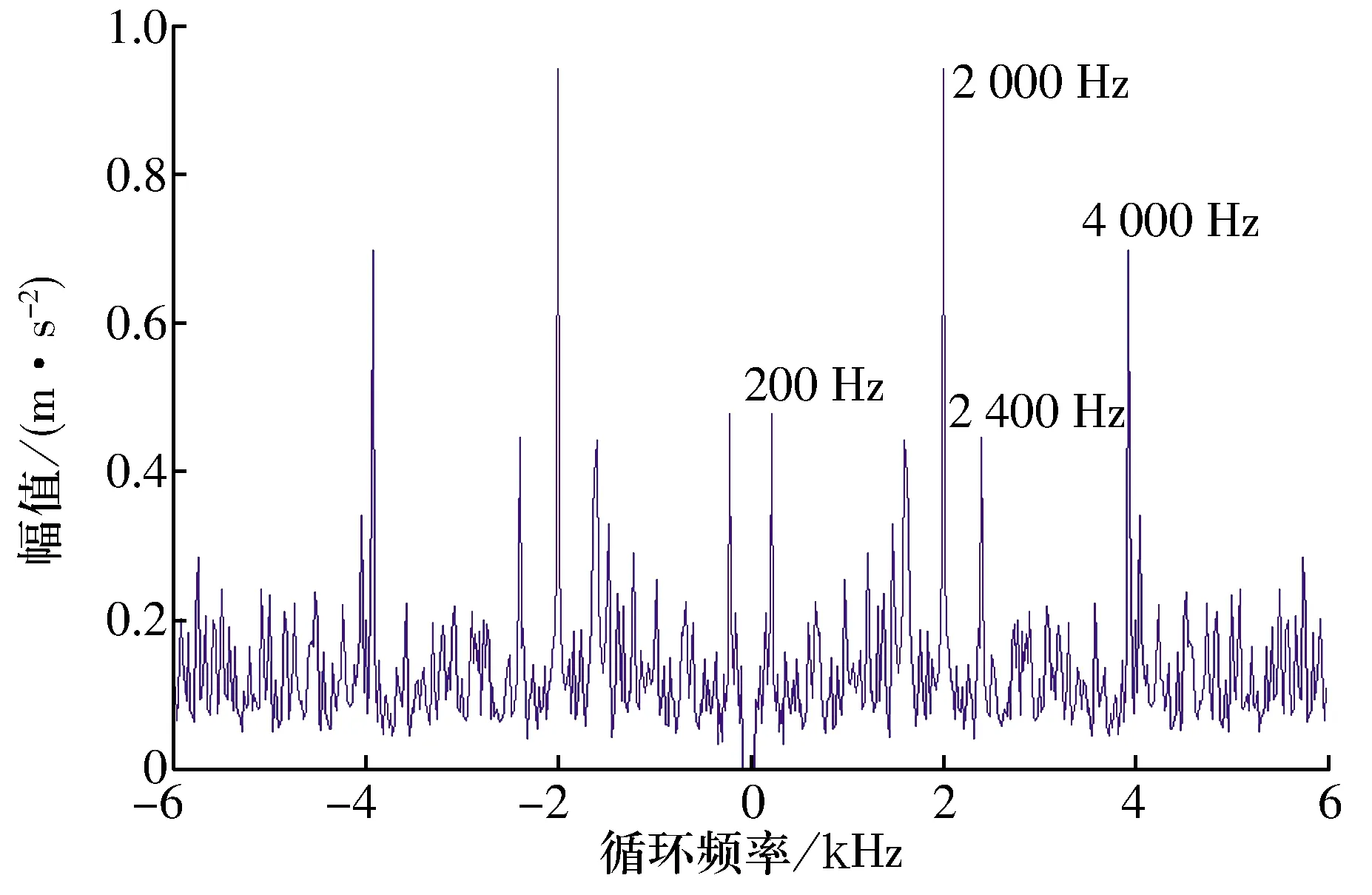
圖13 循環(huán)平穩(wěn)相關熵譜輪廓圖Fig.13 Profile map of cyclostationary correntropy spectrum

為凸顯循環(huán)平穩(wěn)相關熵的降噪能力，將循環(huán)平穩(wěn)相關熵譜密度與傳統(tǒng)基于二階統(tǒng)計量的譜相關密度進行對比，仿真調幅信號的譜相關密度即輪廓圖如圖14所示[23-24]，可以看出信號的能量分散在整個雙頻平面內，譜相關密度的能量聚集性很差，調制頻率和載波頻率完全被噪聲掩蓋，難以有效識別。

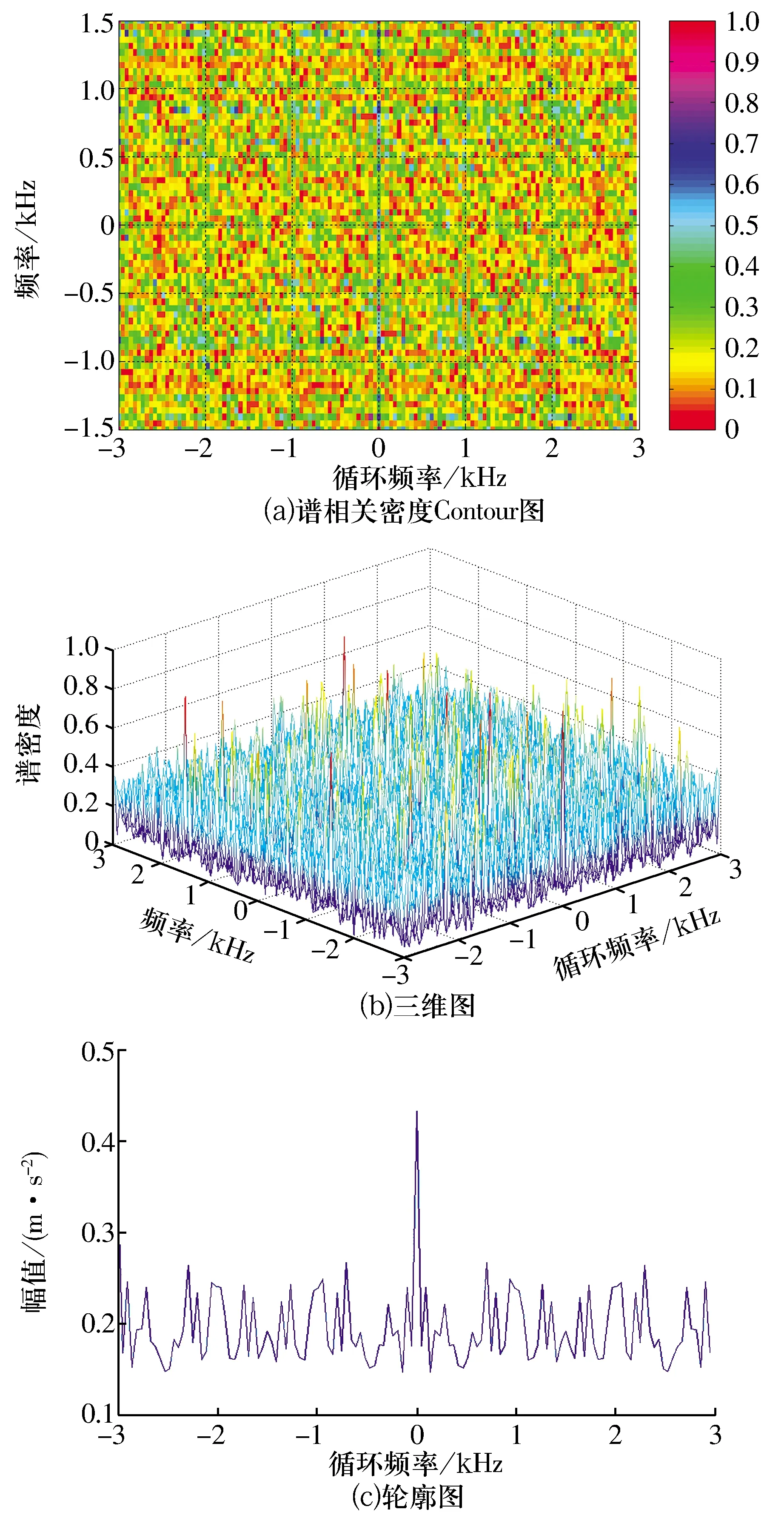
圖14 仿真調幅信號的譜相關密度處理結果Fig.14 Spectral correlation density processing results of simulative amplitude modulation signal

4 實例驗證

采用某型號齒輪箱輸入端軸承進行試驗，電動機額定轉速為1 500 r/min，轉頻fr為25 Hz，采樣頻率為32 768 Hz。軸承型號為6208，球組節(jié)圓直徑為97.5 mm，鋼球直徑為18.33 mm，球數(shù)為10。利用線切割機床分別在軸承內、外圈溝道上加工寬0.8 mm、深1 mm的局部裂紋，以模擬軸承內圈、外圈局部裂紋故障。計算[25]可得軸承內、外圈故障特征頻率fi，fe分別為148.5，101.5 Hz。

4.1 軸承內圈故障

軸承內圈局部裂紋故障振動信號如圖15所示，圖中存在明顯的幅值調制現(xiàn)象，但根據(jù)時域波形及其傅里葉變換無法有效識別軸承故障。

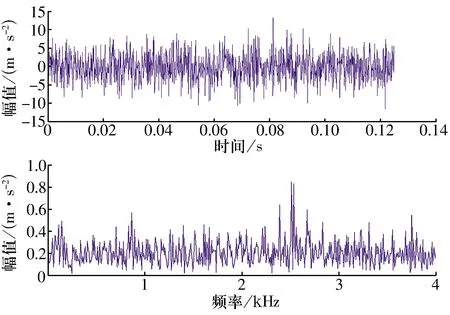
圖15 軸承內圈故障振動信號及其傅里葉變換Fig.15 Vibration signal and its FFT with bearing inner ring fault

軸承內圈故障振動信號的循環(huán)平穩(wěn)相關熵譜密度圖如圖16所示，由圖可知：軸承內圈故障頻譜特征是由循環(huán)頻率α與譜頻率f構成的雙頻平面，軸承內圈故障特征頻率fi及其倍頻主要沿直線f=-0.5α分布，逐漸由頻譜中心向外擴展成整個頻譜平面。

圖16 軸承內圈故障振動信號循環(huán)平穩(wěn)相關熵譜Fig.16 Cyclostationary correntropy spectrum of vibration signal with bearing inner ring fault

根據(jù)(8)式計算可得軸承內圈故障振動信號的循環(huán)平穩(wěn)相關熵譜輪廓，如圖17所示，由圖可知：在循環(huán)頻率α=±fr位置存在顯著的譜峰，對應故障軸承所在軸的調制頻率；在α=±fi±fr，α=±2fi±fr等軸承內圈故障特征頻率及其倍頻位置也存在明顯的譜峰，清晰地刻畫了軸承內圈故障信號的頻譜特征。

圖17 軸承內圈故障循環(huán)平穩(wěn)相關熵譜輪廓圖Fig.17 Profile map of cyclostationary correntropy spectrum with bearing inner ring fault

4.2 軸承外圈故障

滾動軸承外圈局部裂紋故障振動信號如圖18所示，其循環(huán)平穩(wěn)相關熵譜密度圖如圖19所示。由圖可知：在循環(huán)頻率α=±fe,α=±2fe等軸承外圈故障特征頻率及其倍頻位置存在明顯的譜峰，這種頻譜結構清晰表達了軸承外圈故障特征頻率的分布特征。

圖18 軸承外圈故障振動信號及其傅里葉變換Fig.18 Vibration signal and its FFT with bearing outer ring fault

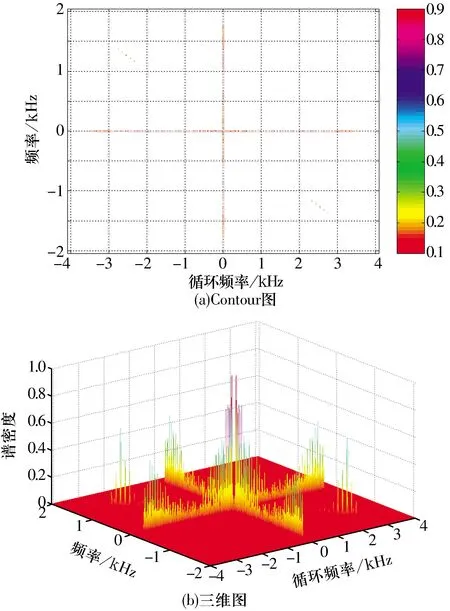
圖19 軸承外圈故障循環(huán)平穩(wěn)相關熵譜Fig.19 Cyclostationary correntropy spectrum of vibration signal with bearing outer ring fault

根據(jù)(8)式計算軸承外圈故障振動信號的循環(huán)平穩(wěn)相關熵譜輪廓，結果如圖20所示，由圖可知,在軸承外圈故障特征頻率fe及其倍頻位置存在明顯的譜峰，清晰反映了軸承外圈故障信號的頻譜特征。

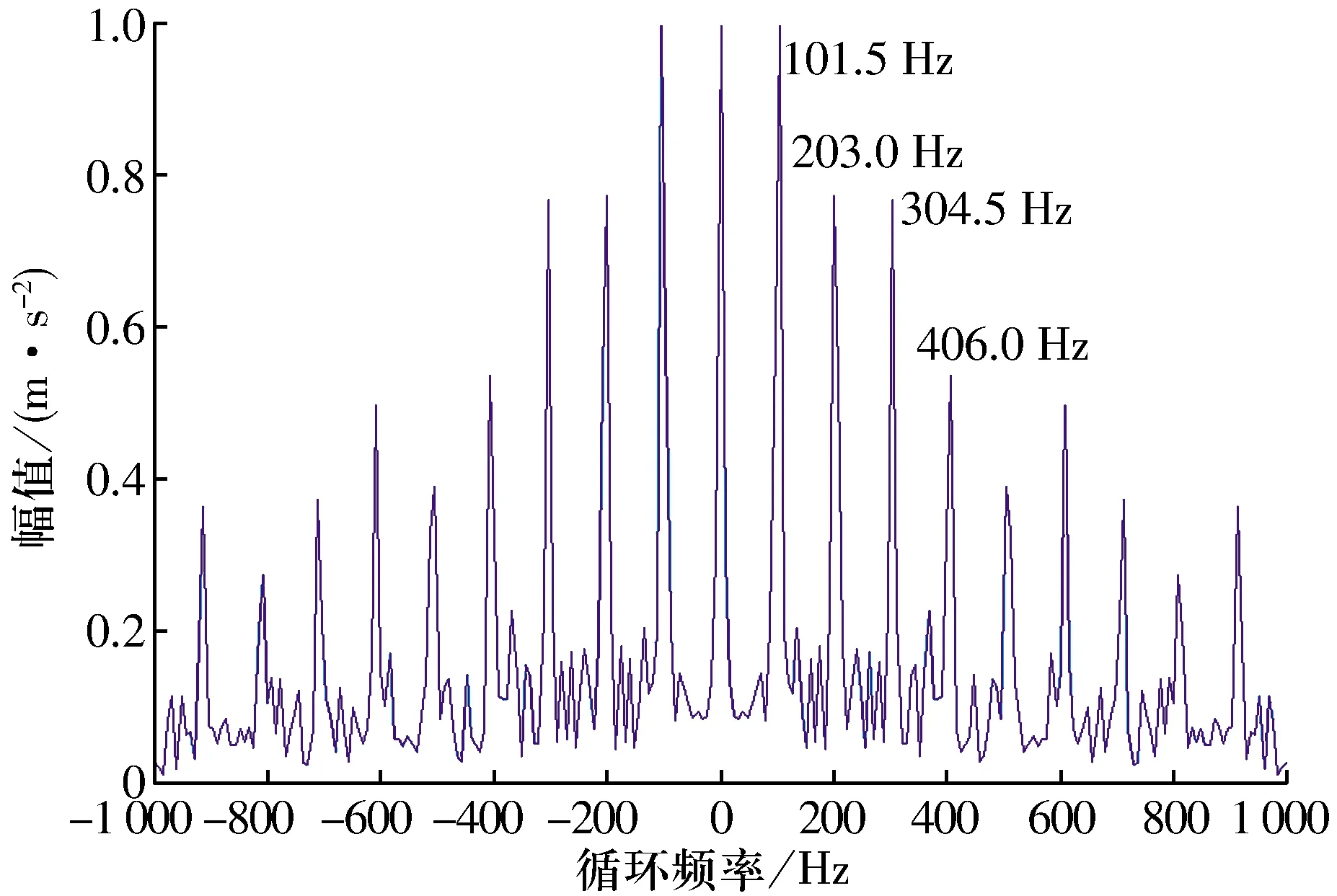
圖20 軸承外圈故障循環(huán)平穩(wěn)相關熵譜輪廓圖Fig.20 Profile map of cyclostationary correntropy spectrum with bearing outer ring fault

4.3 小結

通過上述分析可以看出：循環(huán)平穩(wěn)相關熵具有信號自解調功能，在由譜頻率和循環(huán)頻率組成的雙頻平面內，循環(huán)平穩(wěn)相關熵譜密度能夠清晰地刻畫軸承內、外圈故障信號的頻譜特征，具有從強染噪信號中提取軸承內、外圈故障特征的能力，提高了滾動軸承故障模式識別和特征提取的準確性和可靠性。

5 結束語

以理論分析和幾何圖解等方式系統(tǒng)分析了相關熵的降噪機理，用余弦信號和仿真調幅信號詳細詮釋了相關熵的降噪機理并驗證了其抑制高斯噪聲和隨機脈沖噪聲的能力。基于相關熵提出了循環(huán)平穩(wěn)相關熵譜的軸承故障診斷方法,將循環(huán)平穩(wěn)相關熵譜方法應用于軸承內、外圈局部裂紋故障診斷，試驗結果表明循環(huán)平穩(wěn)相關熵譜密度具有解調功能，能有效提取淹沒在強噪聲環(huán)境中的微弱信號，是一種有效的軸承故障診斷方法。下一步的研究可將循環(huán)平穩(wěn)相關熵應用于風機、內燃機等復雜設備的故障診斷，也可將其作為一種信號預處理手段，與深度學習方法相結合，自動完成故障特征提取和故障模式識別。