面向多機協同的Att-MADDPG圍捕控制方法設計

劉 峰， 魏瑞軒， 丁 超， 姜龍亭， 李 天

(空軍工程大學航空工程學院， 西安， 710051)

無人機集群是一種新型作戰樣式，具有作戰成本低、沖突勝算大、生存能力強、作戰效能高的特點。這些重要特征使得無人機集群在局部沖突中扮演著越來越重要的角色[1-2]。協同圍捕問題屬于無人機集群作戰的典型應用場景之一，有重要的理論研究價值和廣泛的應用前景。

在協同圍捕方法設計上，已有不少學者做了相關研究[3-7]。張紅強等[3]設計了一種基于簡化虛擬受力模型，借助勢域函數使機器人在未知動態環境下完成圍捕。李瑞珍等[4]采用協商法為機器人分配動態圍捕點，建立包含圍捕路徑損耗和包圍效果的目標函數并優化航向角，從而實現協同圍捕。Michael Rubenstein等[5]以1 000個機器人為載體，分邊緣檢測、梯度上升、協同定位3部分算法設計，并通過局部交互進行合作，完成給定圖片的不規則圖形圍捕演示，以人工集群的手段匯聚出自然蜂群的能力。

以上研究均是基于分布式控制，將協同圍捕問題轉換為集群任務分配、路徑規劃、群體一致性問題，從而達到圍捕的效果，但在群體智能涌現方面仍有待提升。

近年來，也有部分學者探索通過強化學習方法來解決協同圍捕問題[8-10]。吳子沉等[8]將圍捕行為離散化后，設計能夠應對復雜環境的圍捕策略，但其存儲機制仍有待優化。陳亮等[9]提出混合DDPG算法，有效協同異構agent之間的工作，同時，Q函數重要信息丟失及過估計等問題有待解決。Ryan Lowe[10]于2017年提出MADDPG算法，采用“集中訓練，分散執行”的框架解決了環境不穩定的問題，但是該算法隨著agent數目的增加，Actor-Critic網絡難以訓練和收斂。

針對以上分析，本文提出一種多無人機協同圍捕算法Att-MADDPG(即Attention-MADDPG)。

1 問題描述

1.1 圍捕環境描述

在一個無限大且無障礙的二維環境中，隨機分布n(n≥3)架圍捕無人機Ui和一架目標無人機T，其速度分別為vi、vT，且滿足vi>vT，航向角分別為φi、φT，其中i∈In={1,2,…,n}，如圖1所示。

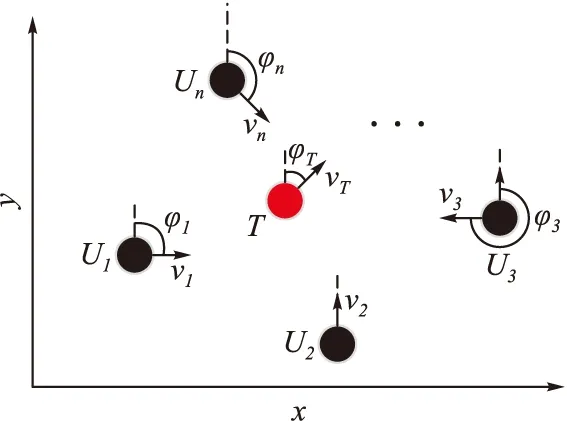
圖1 圍捕環境示意圖

假設對于任意無人機，都能將自身的參數通過通信網絡G實現與其他無人機實時信息交換。本文的目的就是基于這種信息共享，設計控制方法，使n架圍捕無人機通過協作，在有限時間t內，在目標無人機周圍形成圍捕包圍圈，迫使目標無人機T停止運動，從而完成圍捕任務。理想的圍捕包圍圈通常是圍捕無人機群均勻分布在以目標無人機T為圓心，圍捕半徑r的圓上[5]，以n=4為例，理想的圍捕包圍圈如圖2所示。

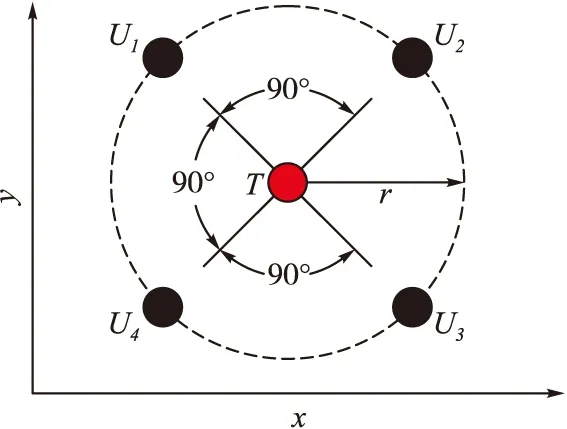
圖2 圍捕包圍圈示意圖

1.2 圍捕無人機模型

設無人機i當前時刻的位置為[x,y]T，構建非線性運動學方程如下：

(1)

式中：ui為無人機的控制輸入，ui∈[-ω0,ω0]；ω0為無人機角速度上限。圍捕控制策略就是根據圍捕態勢確定每架無人機的ui，使圍捕無人機集群實現對目標無人機的有效圍捕。

2 基于強化學習的MADDPG算法

2.1 強化學習理論

強化學習(reinforce learning，RL)是機器學習的一種，不同于監督學習或無監督學習，強化學習是通過與環境的交互進行不斷試錯-學習，以達成回報最大化或實現特定目標，如圖3所示。

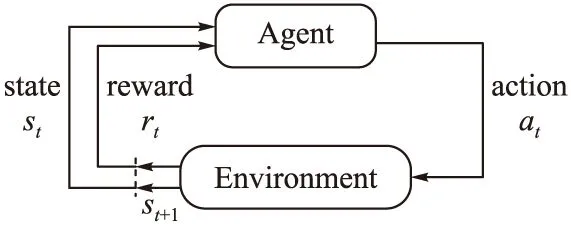
圖3 智能體與環境交互圖

強化學習的常見模型是標準的馬爾可夫決策過程(markov decision process，MDP)。由四元組〈S,A,R,Ps,a〉表示，其中，S表示狀態集，A表示動作集，R表示獎勵函數，Ps,a表示狀態轉移概率。基于當前狀態st，執行動作at，以一定的狀態轉移概率達到下一時刻狀態st+1，獲得即時獎勵Rt，但強化學習是尋找最大化累積回報的學習過程[11]。定義累積獎勵期望值Qπ(s,a)：

(2)

式中：γ為折扣因子，0<γ≤1，表示注重長期獎勵的程度。π為策略，即狀態到動作的映射。給出Q-Learning算法中Q值迭代計算表達式：

Q(st,at)←Q(st,at)+α[Rt+γmaxQ(st+1,at+1)-Q(st,at)]

且st狀態下最優策略為：

Dietterich.T.G[12]從值函數分解的角度，完成了Q-Learning算法中Q值累加的收斂性證明。

2.2 MADDPG算法

多智能體深度確定性策略梯度算法(multi-agent deep deterministic policy gradient，MADDPG)是對深度確定性策略梯度(deep deterministic policy gradient，DDPG)算法進行拓展，使其能夠適用于傳統強化方法無法處理的多智能體合作問題的一種智能算法[10]。MADDPG算法采用“集中訓練，分散執行”的框架進行學習，見圖4。

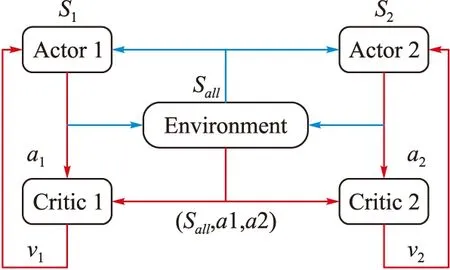
圖4 MADDPG算法流程圖

每個agent擁有一套獨立的Actor-Critic網絡，其中Actor為行動網絡，Critic為評價網絡。在訓練過程中(圖4中紅色部分)，每個agent的Critic獲取全信息狀態，同時包含所有agent的動作。當模型訓練完畢，每個agent的Actor利用局部信息完成與環境的交互(圖4中藍色部分)。令Ot表示agent對環境的觀測，IA和at分別表示Actor的輸入和輸出，IC和Qi分別表示Critic的輸入和輸出，那么對于第i個agent，網絡輸入輸出為：

IA=Ot，at=πi(st)
IC=[Ot,a1,a2,…,an]，Qi=Qi(IC)

(3)

當agent數量增多時，由式(3)中IC可知，Critic的輸入維度也呈線性增長，這將導致網絡難以訓練和收斂。文獻[10]和[13]同樣指出，盡管集中訓練，分散執行的結構具有諸多優勢，但是隨著agent數量的增加，集中訓練中Critic網絡規模會快速增長，因而無法處理大規模多智能體的學習問題。同樣的，由Facebook AI實驗室和Google AI聯合贊助的二維網格環境炸彈人平臺，在測試時最多也只能容納4個agent。

3 基于Att-MADDPG的圍捕控制策略設計

3.1 面向無人機圍捕的Attention機制

近年來，注意力機制(attention mechanism)被廣泛用于基于深度學習的自然語言處理、圖像分類、機器翻譯可視化對齊、語音識別等各種任務中，并取得了不錯的效果[14]。2017年6月，Google機器翻譯團隊借助自注意力機制在WMT2014語料中的英德和英法翻譯任務上取得了優異成績，翻譯錯誤率降低了60%，并且訓練速度遠優于其他主流模型[15]。

圍捕過程中也存在類似的注意力問題。每架無人機更多的關注與自己近鄰的無人機，對距離較遠的無人機的態勢關注的較少，甚至不關注。這就是圍捕過程中的注意力現象。我們將這種現象引入到圍捕策略的設計，形成面向圍捕的注意力機制。以無人機協同圍捕的場景程闡釋注意力機制如下：

定義圍捕無人機集群的聯合動作為Source，待處理信息為Target：

Source=〈p1,p2,…,pm〉

Target=〈q1,q2,…,qn〉

其中，pi(i=1,2,…,m)表示第i架無人機動作，qi(i=1,2,…,n)表示待處理信息。Attention機制[16-17]最常用的是編碼器-解碼器(Encoder-Decoder)框架，如圖5所示。Encoder對輸入的Source進行編碼，通過神經網絡的非線性變換轉化為注意力分布C，C={c1,c2,…,cLp}，其中Lp為Source的長度，Decoder根據注意力分布C和n-1時刻無人機的位置生成n時刻的信息qn，即圍捕無人機集群待處理信息。給出注意力分布ci(i=1,2,…,Lp)的表達式：

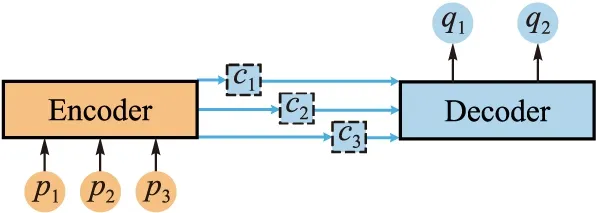
圖5 基于Attention機制的Encoder-Decoder框架

qn=Attention(ci,qn-1)

(4)

式中：wij為Source中第j架無人機的注意力權重系數；pj為Source中第j架無人機的動作信息；Attention為非線性變換函數。

給出基于Attention機制下注意力分布ci的具體計算過程：

1)計算2架圍捕無人機之間的相關性系數：Similarityi=ln(Distanceij/D)，其中Distanceij為兩架圍捕無人機之間距離，D為有效利用區域半徑。

2)引入Softmax函數對第1階段的相關性系數進行歸一化處理，得到注意力權重系數ωi。一方面將原始分值映射成所有元素權重之和為1的概率分布，另一方面通過Softmax的內在機制突出重要元素的注意力權重系數。

(5)

3)根據注意力權重系數對圍捕無人機信息進行加權求和，計算注意力分布ci值。

3.2 基于Att-MADDPG的圍捕控制策略

本文2.2節中分析MADDPG算法由于IC的計算中使用了所有agent的信息，使得其訓練收斂受到影響。因此，我們引入Attention機制對信息進行注意力篩選，從而提高信息的有效利用率，算法框圖如圖6所示。

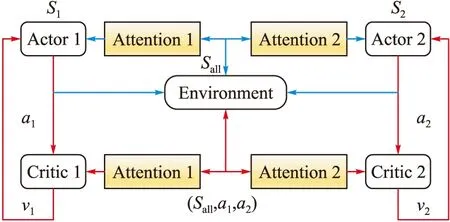
圖6 基于Attention機制改進的MADDPG算法框圖

與MADDPG算法不同之處在于中心化的大腦(即Critic)協調所有圍捕無人機的動作之前，經各自Attention模塊進行非線性處理，對有效利用區域內的圍捕無人機信息進行策略評估(圖6中紅色部分所示)。當模型訓練完畢，依據Actor利用局部信息完成與環境的交互(圖6中藍色部分所示)。則圍捕無人機i的有效利用區域值函數為：

因此，每架圍捕無人機的Critic網絡擬合的是有效利用區域的全局值函數，而非圍捕無人機自身的值函數。這樣，只需要圍捕無人機的策略朝著有效利用區域的全局值函數的方向更新即可。使用MADDPG算法中雙網絡進行更新：

(6)

式中：yi為目標網絡的值函數，由即時獎勵和下一步確定策略值函數構成；L(θi)為目標Critic網絡損失函數，θi為網絡中參數集合。目標Actor網絡和目標Critic網絡采用周期性平穩滑動方法從Actor-Critic網絡中復制參數進行更新。目標Critic網絡損失梯度通過鏈式法則進行求導，其梯度為：

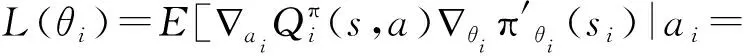
(7)

式中：狀態s為有效利用區域全局觀測；si為圍捕無人機自身觀測。Att-MADDPG算法流程見圖7。

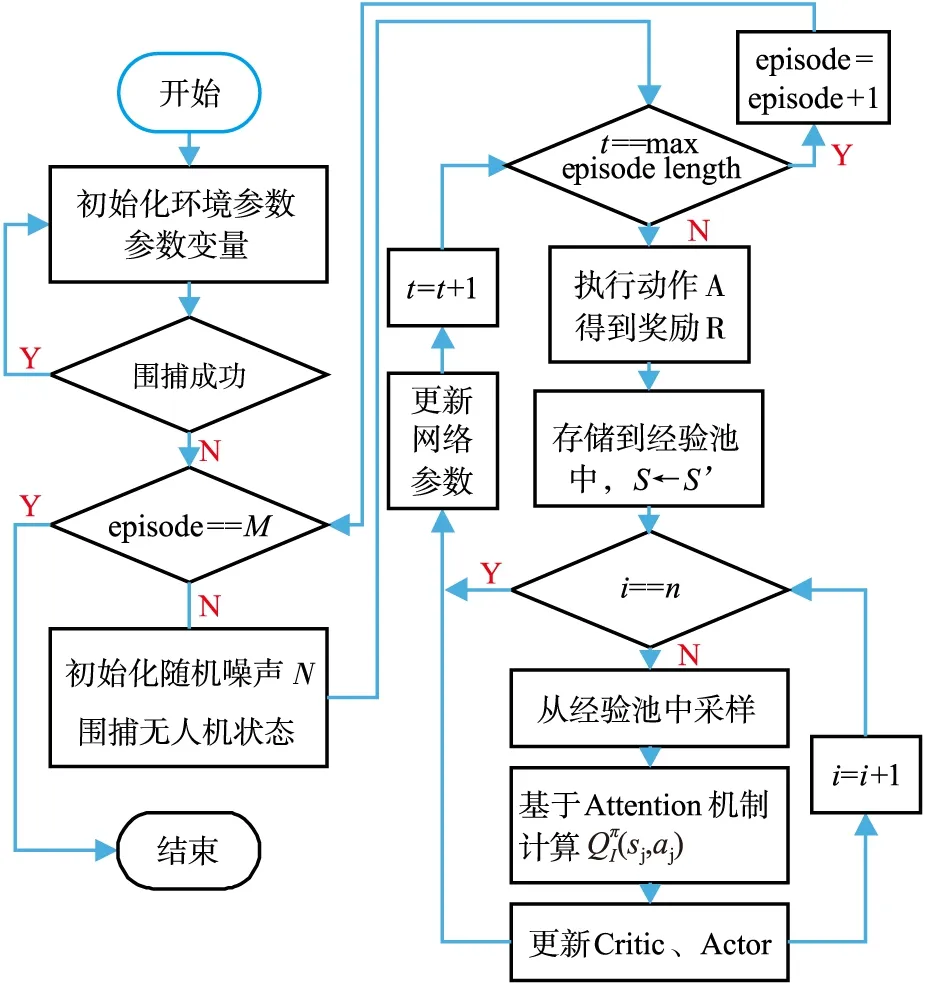
圖7 Att-MADDPG算法流程圖

Att-MADDPG算法偽代碼如下所示：

初始化環境參數、參數變量;判斷是否圍捕成功;for episode=1 to Mdo 初始化隨機噪聲N; 初始化圍捕無人機狀態S; fort=1 to max-episode-length do 每架圍捕無人機采用隨機策略執行一次動作A,與環境交互后得到即時獎勵R,并達到新的狀態S'; 存儲到經驗池中,S←S'; for圍捕無人機i=1 tondo 從經驗池中采樣; 基于Attention機制計算Qπi(sj,aj); 設置目標網絡值函數yj; 基于最小損失函數Lθi 更新Critic; 基于策略梯度‰L(θi)更新Actor; end for 更新每架圍捕無人機網絡參數: θ'i←αθi+(1-α)θ'i end forend for

4 仿真實驗

為驗證所設計Att-MADDPG算法的有效性及智能性，取圍捕無人機數量n=4進行動態協同圍捕仿真實驗，并對比MADDPG算法進行訓練，測試相關性能指標。

4.1 仿真環境配置

設置圍捕無人機獎勵函數如下：

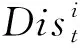
仿真環境參數設置如表1所示。

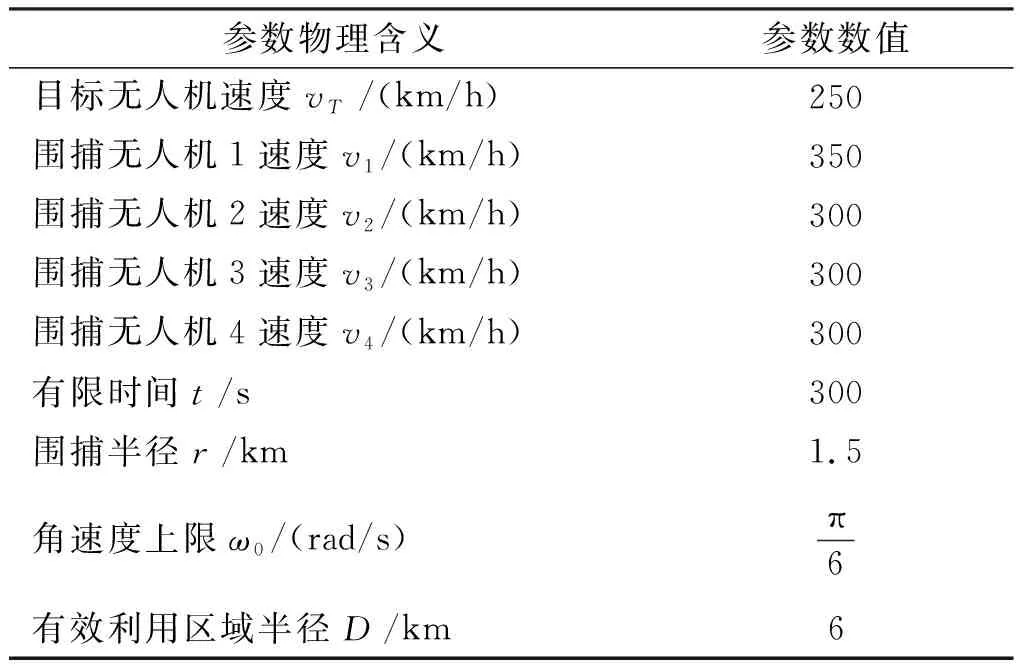
表1 仿真場景設置

配置相同的四機協同圍捕環境，設置相同的獎勵函數，MADDPG算法及Att-MADDPG算法的訓練過程如圖8～9所示。如圖8所示，采用MADDPG算法訓練的圍捕無人機集群大致完成協同圍捕任務，但訓練過程中仍存在一些片段無法有效圍捕。

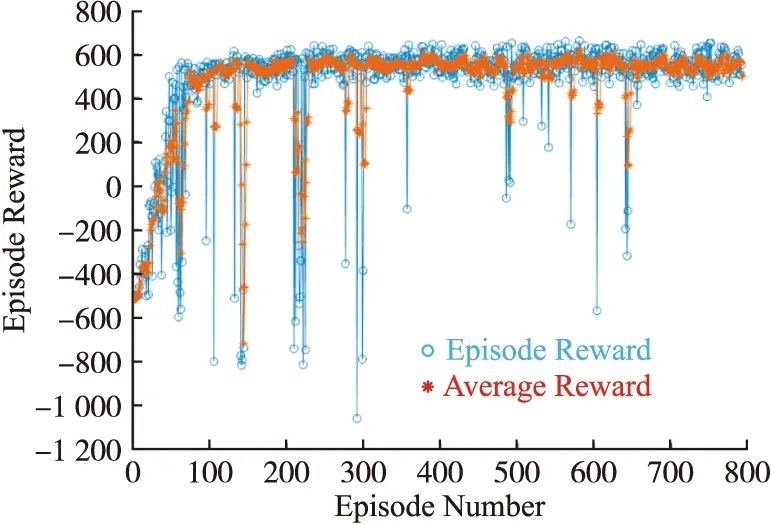
圖8 MADDPG算法訓練過程圖

由圖9可知，經過訓練，Att-MADDPG算法的平均獎勵在150片段后收斂，并大致均勻分布570左右，圍捕無人機集群能夠有效完成協同圍捕任務，并獲得較高獎勵。

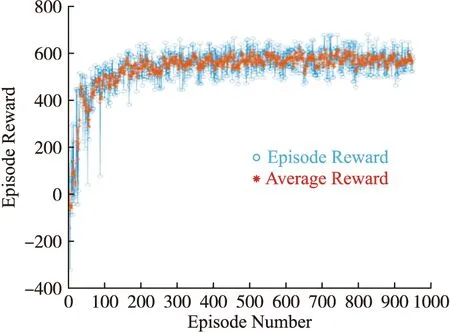
圖9 Att-MADDPG算法訓練過程圖

引入Att-MADDPG算法及MADDPG算法在穩定收斂后1 000個片段的均方差，對比驗證算法的穩定性，見表2。Att-MADDPG算法較MADDPG算法在協同圍捕上更加穩定，根據3σ原則，記錄穩定收斂后1 000個片段不在此范圍內的平均獎勵數目，見表3，Att-MADDPG算法穩定性較MADDPG算法提高8.9%。

表2 穩定收斂后1 000個片段的均方差

表3 1 000個片段內不在3σ原則范圍內的數目

4.2 動態協同圍捕仿真驗證

設定目標無人機的運動策略為固定直線軌跡，對經過Att-MADDPG算法訓練后的4架智能圍捕無人機進行驗證，驗證集參數見表4。

表4 動態協同圍捕驗證集參數

由圖10可知，圍捕無人機通過相互協作完成圍捕。在圍捕過程中，無人機實時判斷圍捕態勢，引入注意力機制觀察有效利用區域半徑內的其他無人機狀態信息，達到形成圍捕包圍圈的目的，各無人機經過協作使系統涌現出更加智能化的協同圍捕行為。

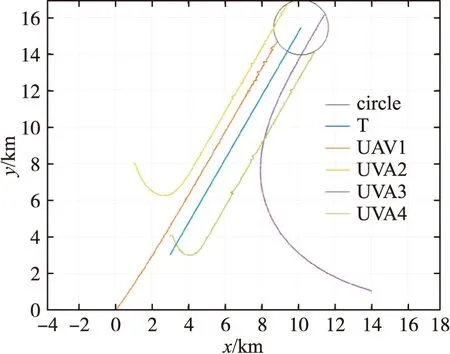
圖10 動態協同圍捕軌跡圖

環境配置相同，采用MADDPG算法進行驗證，Att-MADDPG算法完成協同圍捕總用時264 s，MADDPG算法本文算法總用時326.4 s，減少19.12%。

5 結論

無人機集群作戰在局部沖突中發揮著越來越重要的作用，協同圍捕是無人機集群作戰的典型應用場景之一，也是集群作戰中的重要問題。本文針對MADDPG算法隨著agent數量的增加，訓練難以收斂的不足，基于注意力機制提出Att-MADDPG圍捕控制方法，較MADDPG算法的訓練穩定性提高8.9%，任務完成耗時減少19.12%，且經學習后的圍捕無人機通過協作配合使集群涌現出更具智能化圍捕行為。

為使本文所提算法能夠適用于更加復雜的環境，仍需研究基于群智匯聚的協同圍捕機理，并優化在三維環境下的協同圍捕策略，使圍捕行為更具智能化。