柱面共形陣列DOA與極化參數高效聯合估計算法

齊子森， 彭大林,2， 許 華， 宋佰霖

(1.空軍工程大學信息與導航學院， 西安， 710077； 2.95865部隊， 北京， 102200)

信源方位與極化參數的耦合使得絕大多數高效DOA算法無法應用到共形陣列測向領域，成為了制約共形陣列天線測向算法發展的一個難題。傳統的基于協方差矩陣估計和特征值分解實現噪聲子空間估計的共形陣列測向算法普遍具有計算量大、適用性差的問題[1-4]。已有的共形陣列信源方位與極化參數的聯合估計算法對噪聲子空間的分析處理不夠系統深入[5-7]。文獻[8]通過對陣元局部坐標系進行3次歐拉旋轉變換，實現了共形陣列天線的單元方向圖指向的統一，給出了共形陣列天線陣列流形建模的方法。在此基礎上，文獻[9]通過信源方位與極化參數的去耦合降低了算法的復雜度，實現了信源方位與極化參數的聯合估計，具有普適性好，計算量較小的特點。但是，由于噪聲子空間依然是由傳統特征值分解的方法獲得，所以計算量依然很大。

文中借鑒經典線陣、面陣的高效子空間估計思想[10-14]，給出了一種基于快速子空間估計的柱面共形陣列天線信源方位與極化參數高效聯合估計算法。

1 柱面共形陣列天線的數據模型

對于安裝有N個陣元的柱面共形陣列天線(見圖1)，在遠場中有M個窄帶獨立的點源以平面波入射，加上噪聲擾動后，陣列接收到的快拍數據可表示為：

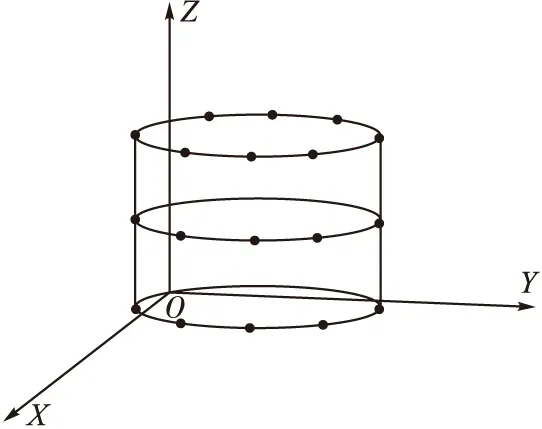
圖1 柱面共形陣列天線

X=A(θ,φ)S+N

(1)

式中:X為N×1快拍數據矢量;S為M×1入射信號復幅度矢量;N為陣列噪聲矢量;A(θ,φ)為N×M陣列的流形矩陣：

A(θ,φ)=[a(θ1,φ1),a(θ2,φ2),…,a(θM,φM)]

(2)

式中：a(θi,φi)為第i個信源的導向矢量，表示為：

a(θi,φi)=[r1(θ1,φ1)exp(-jk0p1?vi),

r2(θ2,φ2)exp(-jk0p2?vi),…,

rN(θN,φN)exp (-jk0pN?vi)]T

(3)

ri=gi·pl=giθ·kθ+giφ·kφ

(4)

gi=giθ(θ,φ)uθ+giφ(θ,φ)uφ

(5)

pl=kθuθ+kφuφ

(6)

uθ=cosθcosφux+cosθsinφuy+sinθuz

(7)

uφ=sinφux+cosφu

(8)

式中：ri為第i個陣元對單位強度入射信號的響應；gi為陣元的單元方向圖；pl為來波信號的極化方式；pi表示第i個陣元在全局坐標系下的位置矢量，vi表示第i個信源在全局坐標系下的方位矢量，k0表示2π/λ0。

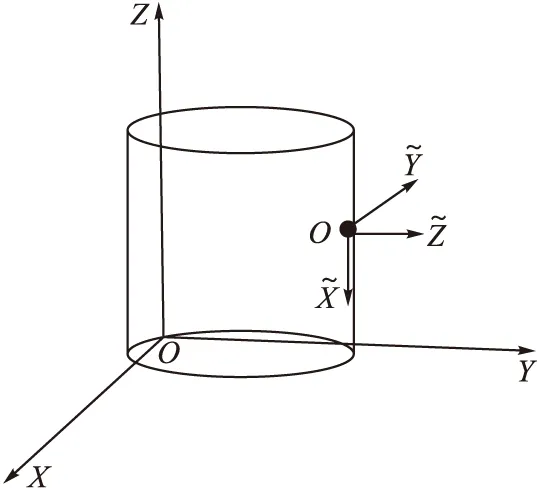
圖2 全局直角坐標系與局部直角坐標系

為了實現陣元單元方向圖的坐標系旋轉變換，我們需要完成以下2個部分：

2)方向圖正交極化分量變換陣列:

全局直角坐標系與陣元局部直角坐標系的旋轉關系可以通過3次歐拉旋轉變換得到，相應的歐拉旋轉矩陣可以表示為[8]：

R(D,E,F)=E(X″,F)E(Y′,E)E(Z,D)=

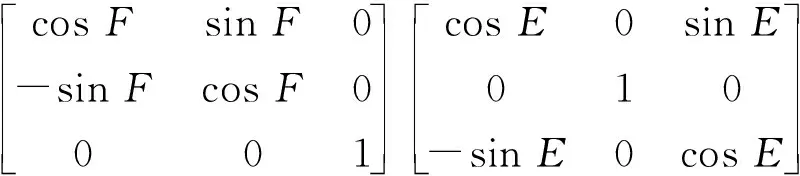
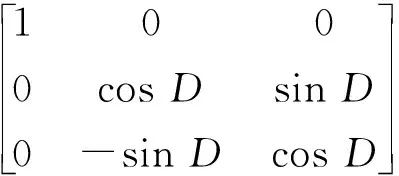
(9)

式中：E(Z,D)表示第1次旋轉以Z軸為旋轉軸，逆時針旋轉角度D的歐拉旋轉矩陣；E(Y′,E)表示第2次旋轉以Y′軸為旋轉軸，逆時針旋轉角度E的歐拉旋轉矩陣；E(X″,F)表示第3次旋轉以X″軸為旋轉軸，逆時針旋轉角度F的歐拉旋轉矩陣。通過合理選擇3次歐拉旋轉的旋轉角度(D,E,F)，E(Z,D)，E(Y′,E)和E(X″,F)可以將陣元的全局直角坐標系旋轉變換為陣元的局部直角坐標系。這種旋轉變換適用于任何幾何結構的共形陣列的陣元的坐標系變換，不同的幾何結構的共形陣列在進行歐拉旋轉變換時對應的歐拉旋轉角度不同。

對于圖3的柱面共形陣列天線，陣元對應的歐拉旋轉角度為：

圖3 柱面共形陣列陣元分布

(10)

式中：n為由下至上的圓陣的序號；m為每層圓環陣中逆時針方向陣元序號；N為圓陣的總層數；M為每層圓陣中陣元的總數。

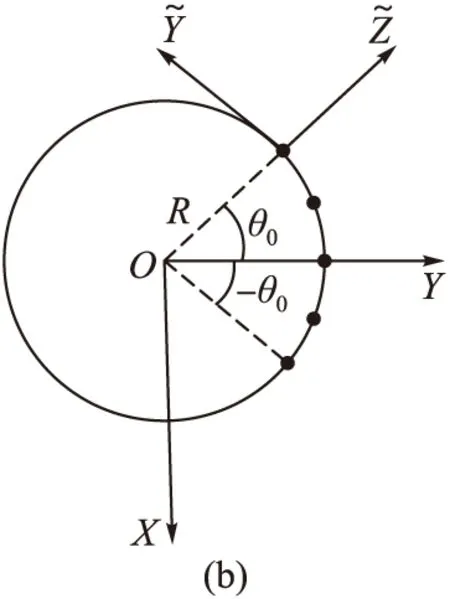
利用式(10)得到的各陣元的歐拉旋轉角度，可以實現柱面共形陣列陣元全局直角坐標系與局部直角坐標系的變換：

R(Dnm,Enm,Fnm)[xnm,ynm,znm]T

(11)

在全局極坐標系內(θ,φ)處的陣元的直角坐標可以表示為：

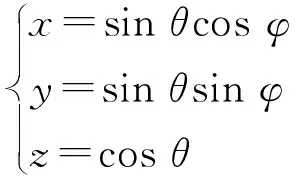
(12)

將式(10)、(12)代入式(11)可以實現陣元全局極坐標系到局部直角坐標系的變換：

[sinθnmcosφnm,sinθnmsinφnm,cosθnm]T

(13)

利用直角坐標系與極坐標系的變換關系，由旋轉所得到的陣元的局部直角坐標得到文中所需要的局部極坐標系中的方位：

(14)

(15)

gnmθ(θ,φ)uθ(θ,φ)+gnmφ(θ,φ)uφ(θ,φ)

(16)

通過式(15)和式(16)的變換，實現了陣元極化方向圖由局部極坐標系到全局極坐系的變換，通過這種變換，便可以建立起具有統一單元方向圖指向柱面共形陣列的數學模型，為實現柱面共形陣列對信源方位與極化參數的聯合估計奠定基礎。

其中:

gnmθ(θ,φ)=(gnmXcosφ+gnmYsinφ)/

cosθgnmφ(θ,φ)=-gnmXsinφ+gnmYcosφ

(17)

將式(4)代入式(3)得：

(18)

aθ(θ,φ)=

[g1θexp (-jk0p1?v),…,gnθexp (-jk0pn?v)]T

(19)

aφ(θ,φ)=

[g1φexp (-jk0p1?v),…,gmφexp (-jk0pn?v)]T

(20)

忽略絕對相位信息，極化參數可表示為：

(21)

式中:k為任意實數;e-jδ(0<δ≤2π)為相位差。因此噪聲擾動后的快拍數據也可以表示為：

X=AS+N=(AθKθ+AφKφ)S+N

(22)

S=[s1,s2,…,sm]T

(23)

N=[n1,n2,…,nm]T

(24)

Aθ=[aθ(θ1,φ1),aθ(θ2,φ2),…,aθ(θm,φm)]

(25)

Aφ=[aφ(θ1,φ1),aφ(θ2,φ2),…,aφ(θm,φm)]

(26)

Kθ=Im×m

(27)

Kφ=diag(k1e-jδ1,k2e-jδ2,…,kme-jδm)

(28)

式(22)～(28)中：A表示流形矩陣；S是信號矢量；N為加性高斯白噪聲；θi,φi分別表示第i個入射信號的俯仰角與方位角。

2 柱面共形陣列天線信源方位與極化狀態的高效聯合估計算法

2.1 基于特征值分解的聯合估計算法

柱面共形陣列輸出數據的協方差矩陣：

R=E[XXH]=ARSAH+σ2I

(29)

對協方差矩陣R進行特征值分解：

(30)

式中：US和UN分別由M個大特征值和N-M個小特征值對應的特征矢量構成；ΣS和ΣN分別為M個大特征值和N-M個小特征值構成的對角陣。當快拍數L有限時，R的統計一致估計為：

(31)

根據子空間原理有：

(32)

將式(18)和(21)代入式(32)得[9]：

(33)

(34)

由秩損理論，當且僅當θ,φ取信源的真實方位時矩陣Q秩損，因此

(35)

umin=umin[Q]

(36)

進一步解得：

(37)

(38)

式中：umin[·]為求矩陣最小特征值對應特征向量的算子。

2.2 柱面共形陣列天線的快速子空間估計

對柱面共形陣列接收數據的協方差矩陣進行特征值分解：

(39)

VS的列數等于信源協方差RS的秩M，從而張成A(θ,φ)的M維子空間，這里M表示信源數，由式(29)和式(39)得：

VS=AQ

(40)

式中：Q=RSAHVS(ΛS-σ23I)-1∈CM×M是滿秩矩陣。

多級維納濾波器的每一級匹配濾波器均是前一級期望信號與觀測信號的互相關函數的歸一化矢量，即:

(41)

且相互正交，所以級數為N的MSWF相當于維納-霍夫方程在Krylov子空間即：

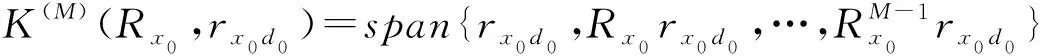
span{h1,h2,…,hM}=

(42)

所以存在一個滿秩矩陣K∈CM×M，使得：

[h1,h2,…,hM]=

(43)

i=0,1,…,M-1

(44)

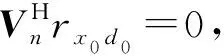
AQΓK=AH

(45)

其中:

∈CM×M

(46)

H=QΓK∈CM×M

(47)

因為Q和K均是非奇異矩陣，所以H也是非奇異矩陣。由式(45)可得：

(48)

(49)

即TS與信號子空間等價，Tn與噪聲子空間等價。

2.3 基于多級維納濾波器的聯合估計算法

為了降低常規子空間估計的計算復雜度，最有效的方法就是避開協方差估計和特征值分解。事實上，當給定某一信號的波形，由多級維納濾波器的前向分解就可以實現信號子空間和噪聲子空間的快速估計[15]。

基于多級維納濾波器構建噪聲子空間的算法如下：

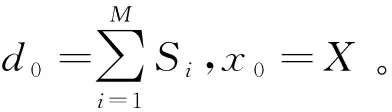
步驟2前向遞推：

Fori=1,2,…,N

xi=xi-1-hidi

(50)

式中：di是各級期望信號；xi是各級觀測信號。

信號子空間和噪聲子空間由各級濾波器組成：

US=span{h1,h2,…,hM},

UN=span{hM+1,hM+2,…,hN}

(51)

后續步驟與2.1節算法相同。

綜上所述，本文提出的基于多級維納濾波器的柱面共形陣列天線信源方位和極化參數高效聯合估計算法步驟總結如下：

步驟1獲得目標點源的信號波形和柱面共形陣列天線接收到的快拍數據。

步驟2根據式(50)進行維納濾波器的前向遞推獲得各級濾波器函數。

步驟3根據式(51)獲得噪聲子空間。

步驟4根據式(34)和(35)進行空間譜搜索獲得目標方位。

步驟5根據式(36)、(37)和(38)進行目標信號的極化參數配對。

3 算法性能分析

3.1 算法復雜度分析與比較

文獻[9]通過將信源方位與極化參數去耦合降低了譜峰搜索的維數，減小了運算量，但因為依然利用協方差估計和特征值分解的方法獲得噪聲子空間，所以利用柱面共形陣列實現參數聯合估計所需的運算量為O(N3+N2L)，其中L為快拍數。本文在柱面共形陣列快拍數據構建噪聲子空間的過程中因為只利用到了目標信號的波形和多級維納濾波器的前向分解，并不涉及多級維納濾波器的后向合成，更不涉及協方差的估計和特征值的分解，因此運算量為O(N2L)[15]。因此本文柱面共形陣列信源方位與極化參數聯合估計算法更為高效。2種算法運算量對比見表1。

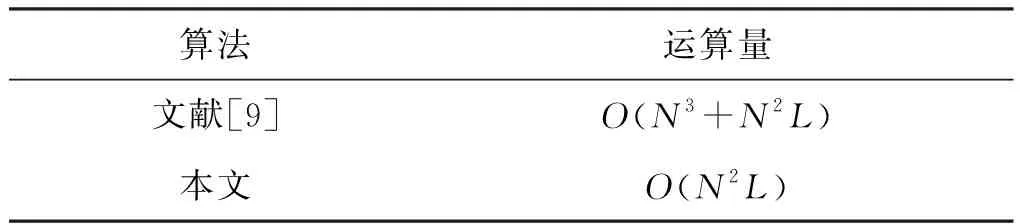
表1 算法運算量對比分析

進行仿真實驗以驗證本文提出的高效聯合估計算法的性能。仿真實驗中，假設在遠場有2個獨立、窄帶、方位分別為θ1=30°、φ1=90°、θ2=60°、φ2=120°，極化參數完全相同，垂直水平極化模值和相位差分別為k1=1、k2=2、δ1=π/4、δ2=π/3的信源以平面波入射到如圖3的柱面共形陣列，圖中每層陣元間隔半波長，柱面橫截面半徑為2倍波長。在小樣本支撐的信號環境中，本文算法具有對文獻[9]聯合估計算法計算量上的明顯優勢，因此實驗中2種算法采用不同的快拍數進行仿真對比。

1)實驗1角度估計的速度仿真

聯合估計算法的高效性通過角度估計速度可以比較直觀地反映出來。在本實驗中，角度估計速度利用在不同信源數條件下的角度估計時間來衡量，實驗中取蒙特卡羅實驗運行時間的平均值作為單次估計時間。

仿真條件：信噪比設為15 dB，蒙特卡羅實驗次數為2 000，文獻[9]快拍數為3 000，本文算法快拍數設為3 000，陣元數由20變化到100，估計時間和陣元數關系的仿真如表2所示。

由表2可以看出，在整個陣元數的變化范圍內，本文高效聯合估計算法的單次估計時間始終低于文獻[9]算法的單次估計時間，并逐漸拉開時間上的差距，驗證了本文算法在計算量上的優勢，證明了本文算法相對于以往聯合估計算法的高效性和巨大的實用價值。

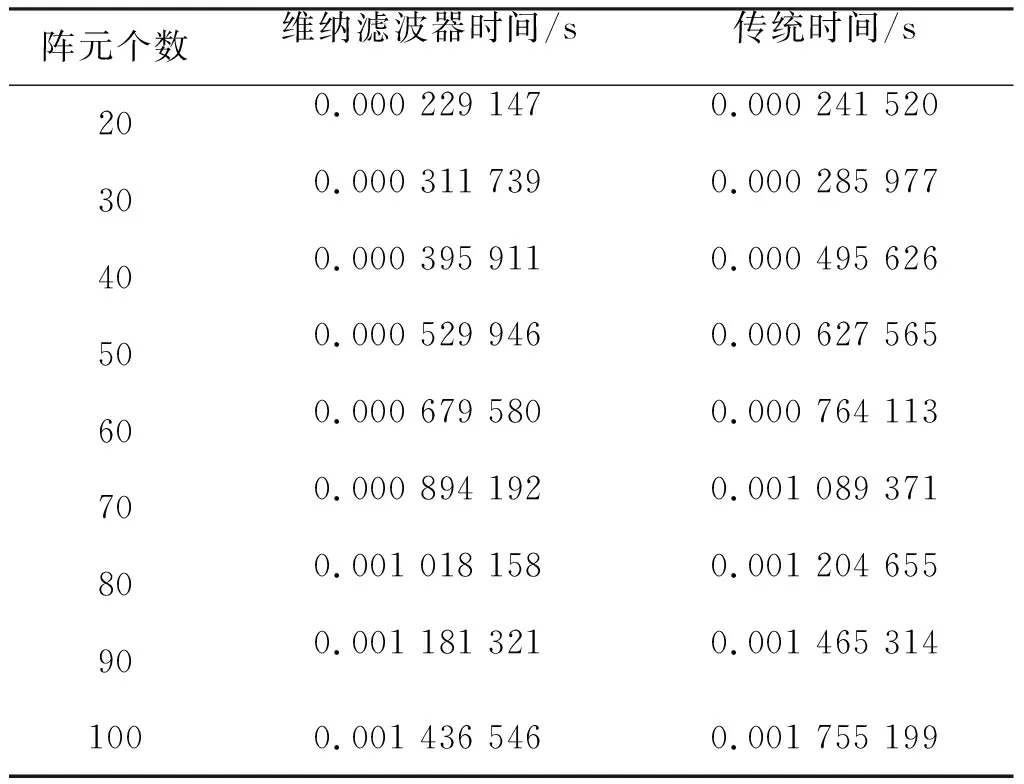
表2 算法運算量對比分析

2)實驗2均方根誤差的仿真

算法的均方根誤差隨信噪比的變化情況可以反映算法的估計精度。

仿真條件：文獻[9]快拍數設為500，本文高效算法快拍數設為500，蒙特卡羅實驗次數設為500，信噪比由-5 dB變化到15 dB，仿真結果如圖4所示。

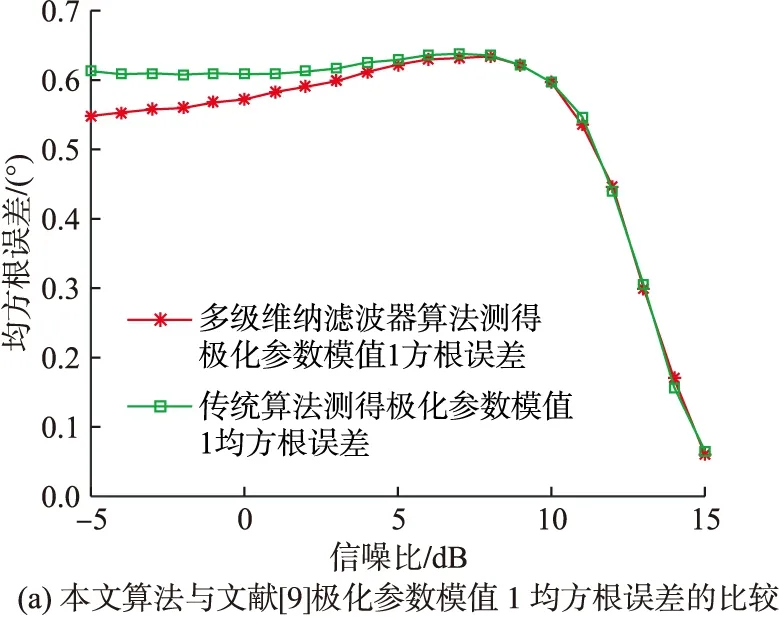
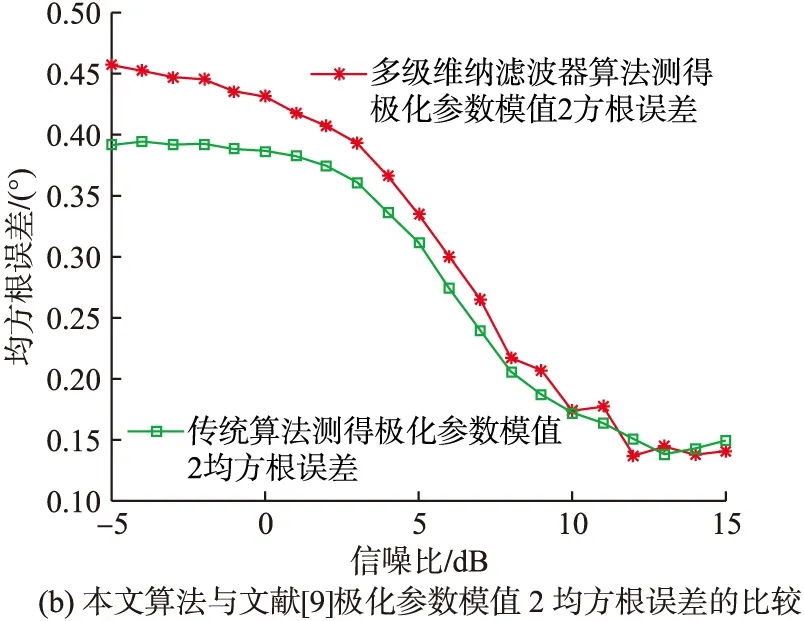
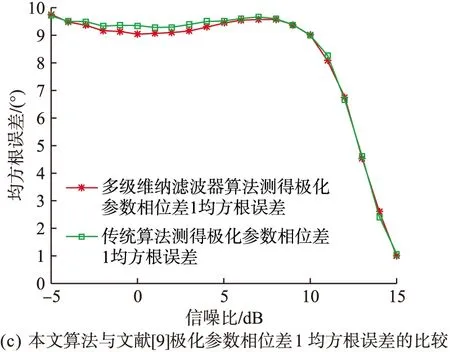
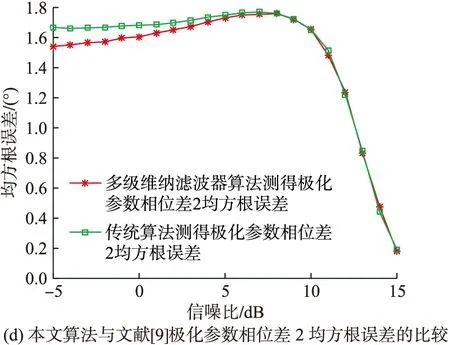
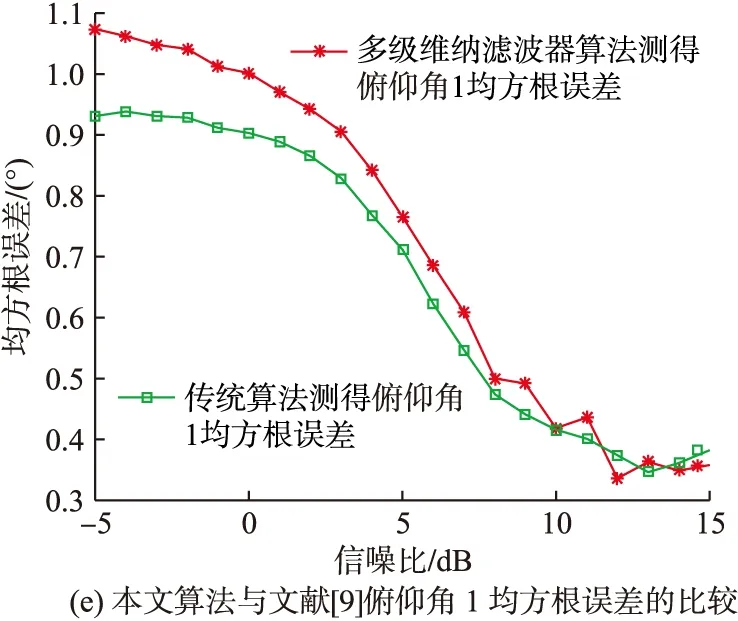
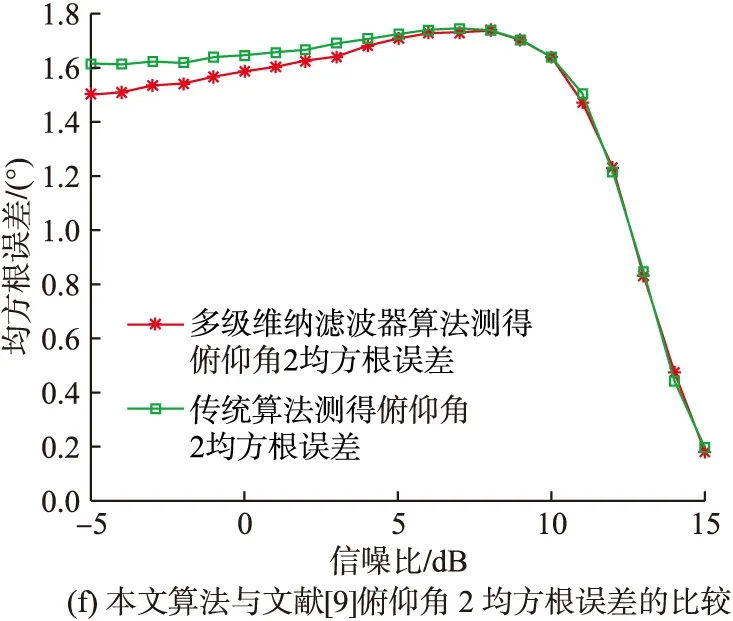
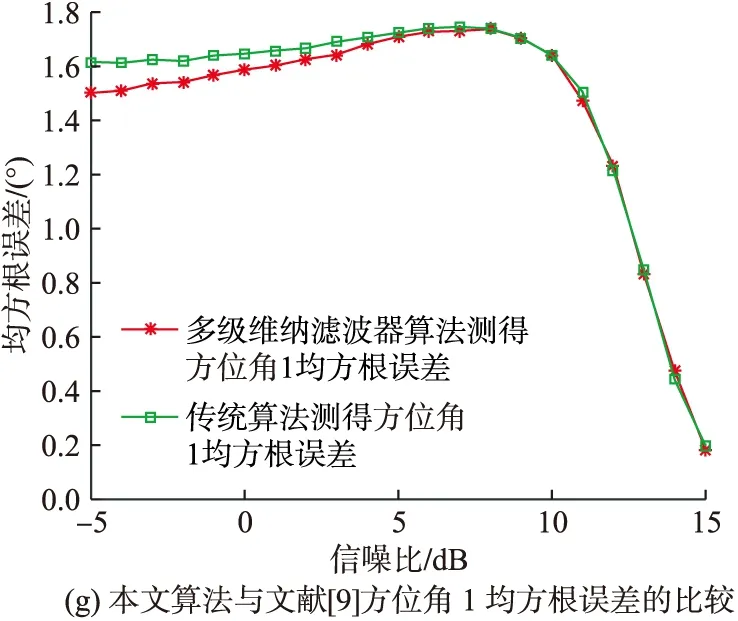
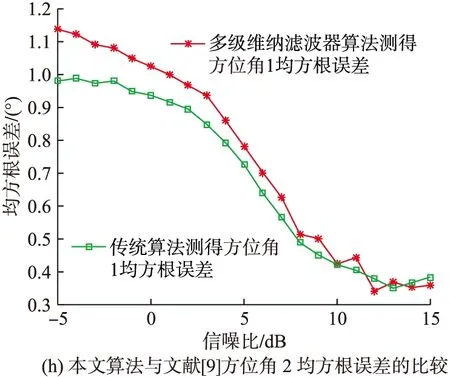
圖4 均方根誤差與信噪比的關系

由圖4可以看出，在整個信噪比的變化范圍內，本文的高效聯合估計算法對極化參數和來波方位的估計值均方根誤差與文獻[9]算法估計值均方根誤差大致相當，說明在一定的信噪比變化范圍內，本文的高效聯合估計算法的估計精度與文獻[9]算法的估計精度大致相當。此外，在信噪比大于10 dB的條件下，本文算法對各項參數(極化參數相位差除外)的估計均方根誤差均小于1，這樣的估計精度在大多數工程應用中是可以被接受的。

綜上分析，在一定的估計精度要求下，本文的聯合估計算法在小樣本支撐的信號環境中對嚴重依賴信號樣本數保證估計精度的文獻[9]具有計算量上的一定優勢，但也依然存在一些不足：計算優勢嚴重依賴快拍數、計算精度受制于快拍數和陣元數過多也會減小本文高效算法的計算優勢。

4 結語

本文提出的算法在文獻[9]的基礎上，利用多級維納濾波器的前向遞推代替以往的協方差估計和特征值分解以進行譜峰搜索和極化參數配對，在一定程度上減小了聯合估計算法的運算量的同時，保證了算法的估計精度，對于算法的工程實現具有重要意義。