一種ARIMA-LSTM組合模型的人參價格預測方案研究
方 濤
(河北省地質大學,河北 石家莊 050030)
0 引言
隨著國家政策的推廣和中藥材自身卓越的治療效果,中藥材市場由國內擴展至全球,需求量逐漸擴大,而中藥材價格又受到其生長周期、需求周期、政策等多方面、多因素的影響,波動幅度較大,沒有顯著的線性變化趨勢[1]。相比于常見的季節性農產品價格,中藥材價格也沒有明顯的周期變化規律。以常見的名貴中藥材人參為例,在2015年1月至2020年11月,價格最高為650元/kg,最低為280元/kg,變化幅度超過了130%,劇變的價格對于人參的種植和銷售都會帶來不良的影響。
人參的價格數據是一個復雜的包含線性變化、非線性變化的系統,很難將它確定為一種單純的線性模型或者非線性模型,這一特性增加了預測的難度[2]。在此背景下,為了提高預測精度,提出一種 ARIMA-LSTM神經網絡組合模型,分別對人參價格的線性、非線性成分進行預測。價格數據是按照時間的先后順序收集的,可以將其視為時間序列數據,而中藥材或是由于技術改良,導致成本降低,價格下降;或是需求量逐年增加,導致價格上升,這些都是線性變化成分,ARIMA模型廣泛應用于確定的、線性的變化系統,使用ARIMA可得到線性變化趨勢。原始數據減去ARIMA預測的線性部分,可得到只剩下非線性特征的殘差數據,LSTM 神經網絡具有映射任意非線性函數的能力,又因為其特殊的記憶單元、遺忘門等結構,擅長處理時間序列數據,對包含非線性特征的殘差序列數據可得到一個良好的預測結果。組合模型避免了單一模型的固有缺陷,為價格預測提供一種更有效的預測模型。
國外的研究者,如美國經濟學家 Moore[3]通過對每一年溫度變化和降雨量做相關性分析,使用回歸模型研究棉花價格與溫度、降雨量這兩個相關因素之間的關系,以此對棉花價格做出預測,并且根據預測結果證明了該回歸模型的精度要優于傳統的分析方法;Jarrett[4]首次將時間序列模型應用在澳大利亞羊毛價格預測上,得到羊毛價格的大致趨勢,驗證了該模型在線性預測方面良好的性能表現,為價格預測提供更多的思路,引來更多的學者對時間序列模型展開更深入的研究和廣泛的應用。而國內的研究者,如潘水洋[5]等提出一種用神經網絡預測股票收益的模型,學習和捕獲定價因子之間的非線性關系,獲得良好的預測結果;張東青[6]等在使用神經網絡的基礎上,使用分位數回歸分析了不同價格條件的分布特征,提出的是基于神經網絡優化后的模型,實驗結果表明,分位數回歸得到分布特征為神經網絡提供的額外的參考依據并提高了預測精度。但是總體來說,這些研究都是使用單一的模型對事物的發展進行預測,盡管使用優化方法對模型進行改進,但是從結果來看,效果并不佳,本文針對藥材價格數據的不同特性,使用雙模型分別對線性和非線性特征進行分析預測,從結果上來看,預測效果要優于單一的模型。
1 模型理論
1.1 ARIMA模型
ARIMA(Autoregressive Integrated Moving Average,整合自回歸移動平均)是在AR和MA模型的基礎上改進而來[7]。
AR(Autoregressive Model,自回歸)模型是統計上一種處理時間序列的方法,用待研究數據中一段歷史時期的數據來預測下一個或多個時期的結果[8]。如使用x1至xt–1時期的數據預測xt時刻的數據。使用該模型的前提是這些數據之間具有線性關系。AR模型的特征是使用自變量預測自變量。該模型定義如下。
給定序列{xt},某一個時刻t和前p個時刻序列值之間的關系為:
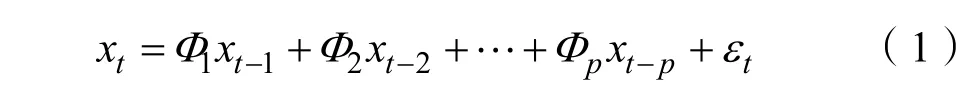
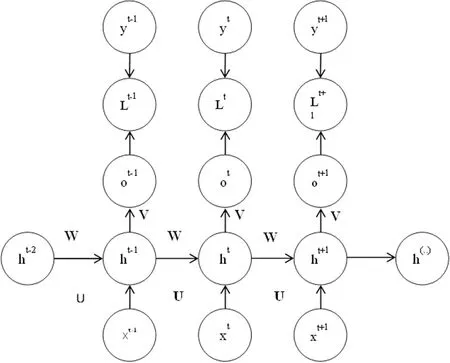
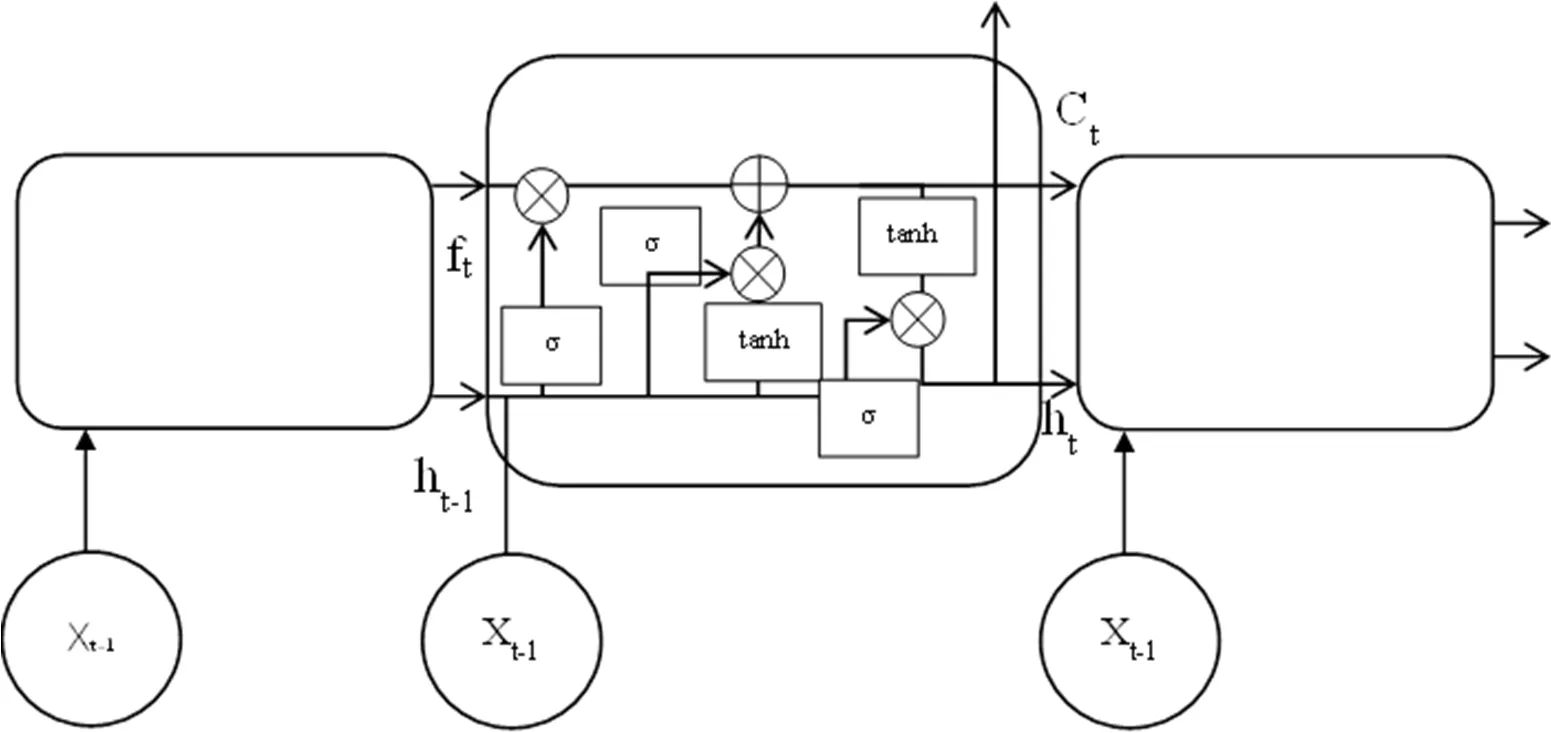
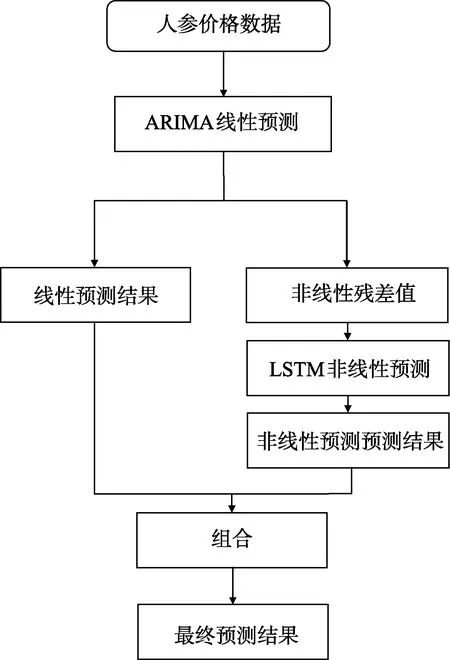
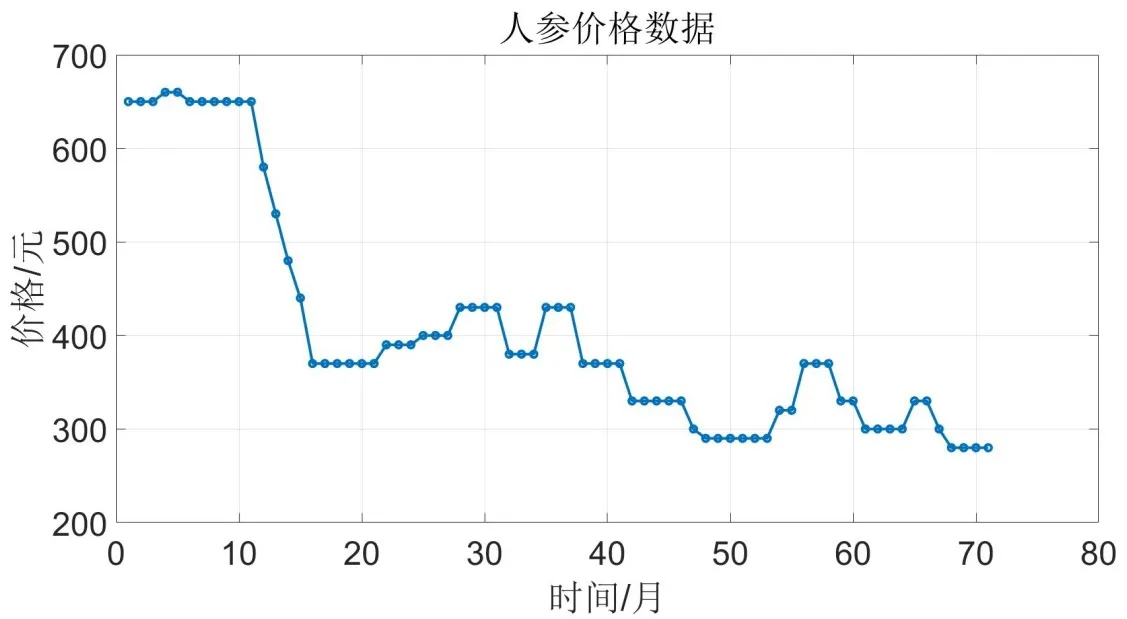
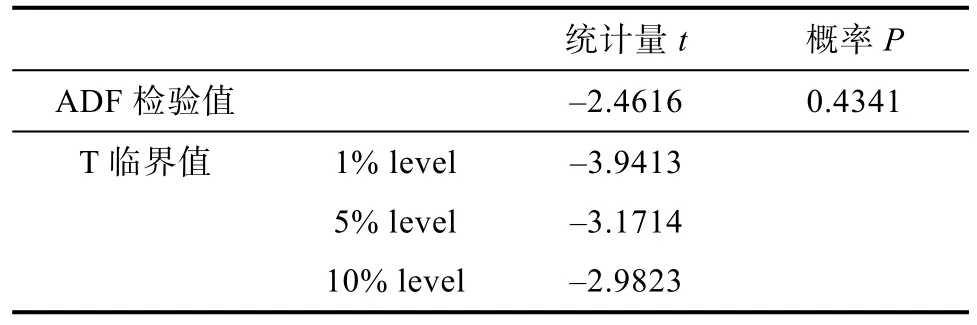
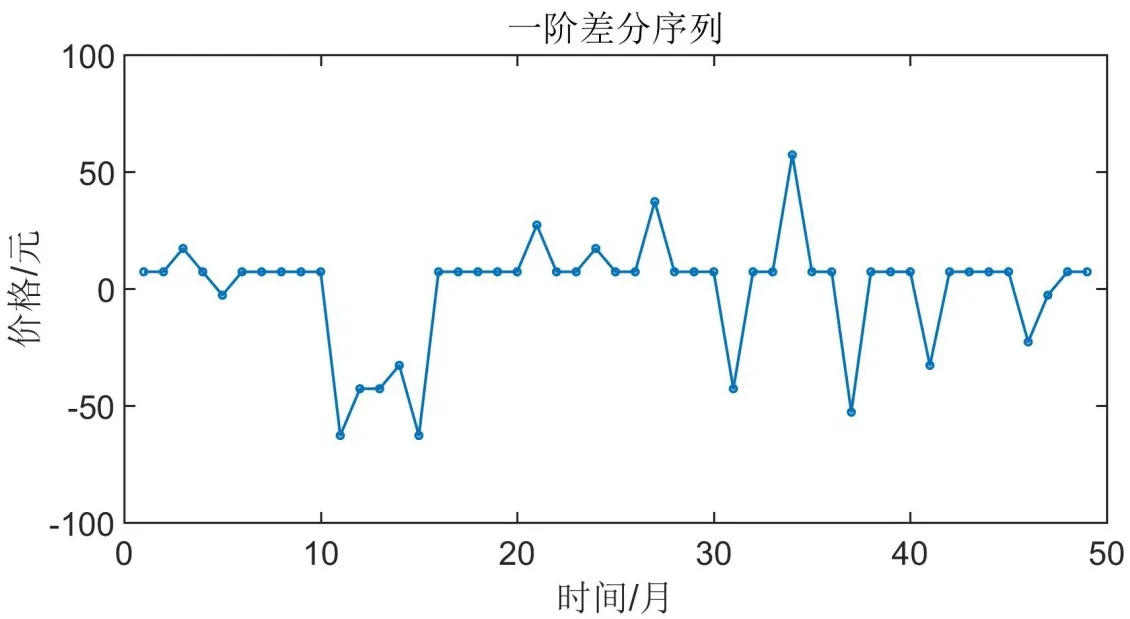
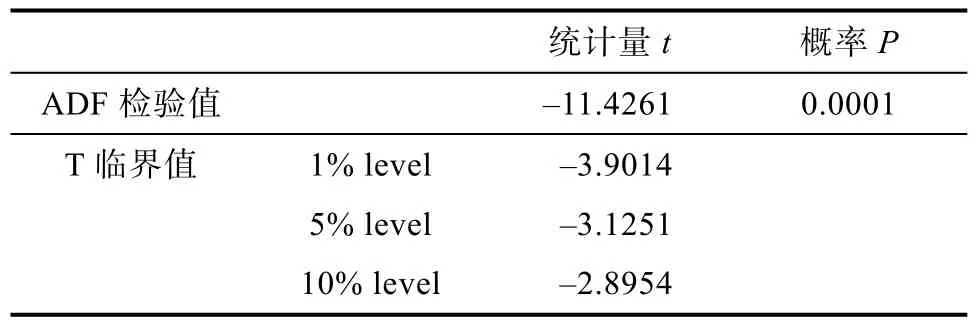
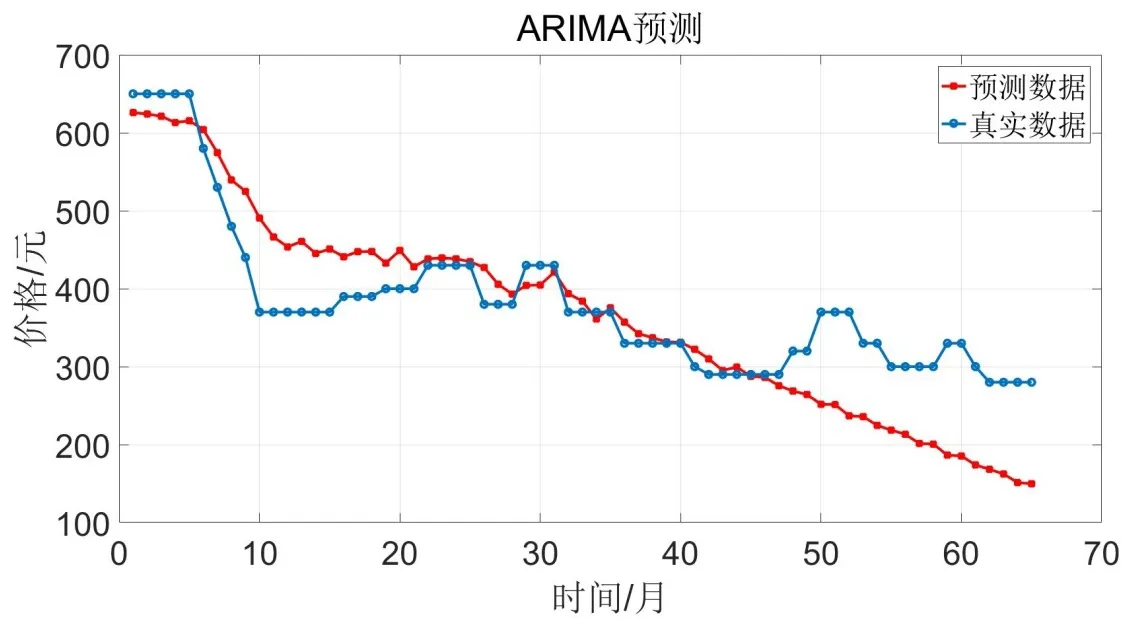
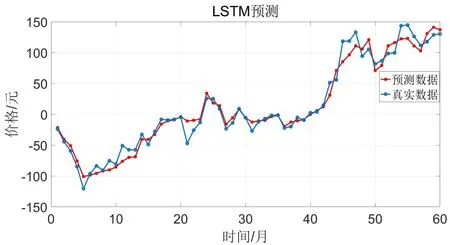
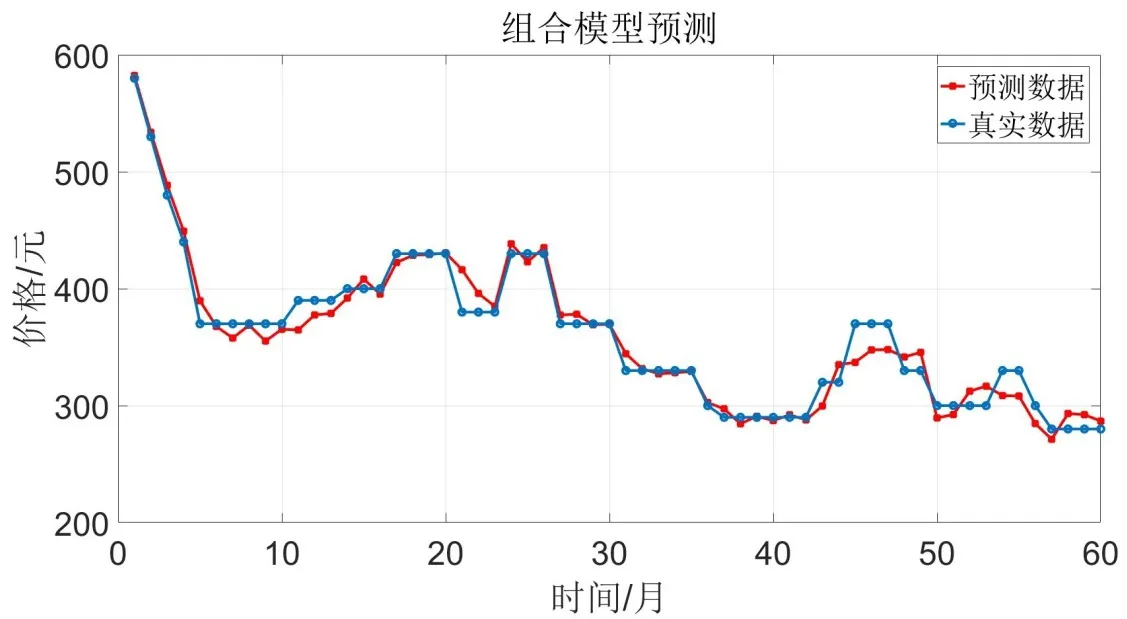
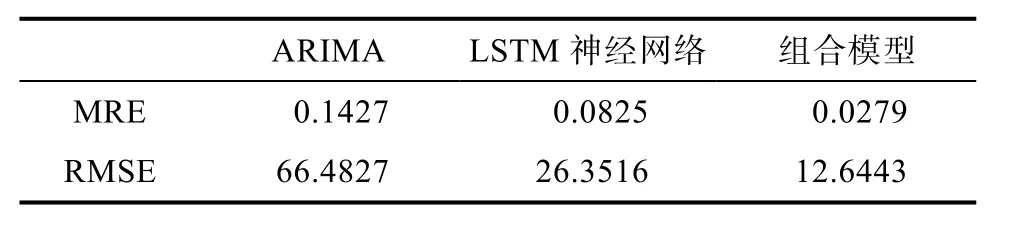
假設隨機序列{εt}是白噪聲,若其與前一時刻序xt(k MA(Moving Average Model,移動平均)模型是一種平滑預測技術,它的基本思想是將待研究的數據逐項推移,依次計算序列平均值,以顯示該序列長短期趨勢的變化[9]。MA模型可以使原本受各種影響影響導致波動大、較難看出其變化的序列顯示出它內在的趨勢。該模型的定義如下。 給定序列{xt},xt是若干個白噪聲的加權平均和: 式(2)中,{εt}是白噪聲序列,這樣的模型稱為q階移動平均模型,記為MA(q)[10]。 由于AR、MA模型存在只能適用于平穩時間序列的缺點,提出ARIMA模型,該模型基于AR、MA模型,公式可表示為: 記為ARIMA(p,d,q)[10]。 ARIMA模型綜合了AR、MA模型對線性趨勢有良好預測能力的優點,由于含有限參數,只要通過一些方法計算、估計這些參數的值,模型即可完全確定。同時 ARIMA模型使用差分法消除時間序列中與線性預測不相干的不平穩因素,預測性能和適用范圍都更為優秀,更適合于預測價格序列中的線性趨勢。 LSTM(Long-Short Term Memory,長短期記憶)神經網絡是RNN(Recurrent Neural Network,循環神經網絡)的一種變體,其基本結構與RNN類似[11]。LSTM神經網絡在傳統神經網絡的結構基礎上,添加了記憶單元,同一層的神經網絡之間使用相同的權重,因此特別適合處理時間序列數據[12]。序列數據可以是價格數據,也可以是文字序列。這些數據有一個共同特點:反應某一個事物、狀態等隨時間而發生變化,即后面時間段的數據受之前某一時刻或者某一段時間數據的影響。LSTM 神經網絡的結構區別于一般的神經網絡同層之間不連接,它的所有節點(循環單元)均按鏈式連接,結構圖如圖1所示。 圖1 LSTM神經網絡結構圖Fig.1 LSTM neural network structure LSTM 神經網絡的網絡拓撲結構整體上與傳統神經網絡類似,由輸入層、輸出層、隱含層三層組成,因為記憶單元和遺忘門的存在,對于包含非線性特征的時間序列數據具有較好的記憶和預測能力,故適合用在價格預測上。LSTM 神經網絡的結構基于RNN的結構,區別在于隱含層的改變,內部詳細的模型圖如圖2所示。 圖2 LSTM神經網絡模型圖Fig.2 LSTM neural network model LSTM神經網絡對比RNN最大的改進是它增加了遺忘門、輸入門、輸出門和一個記憶單元,可以通過控制門控單元對輸入數據選擇性的進行記憶和遺忘[13]。若輸入數據為x1、x2…xt–1、xt、xt+1,遺忘門的計算公式為: 其中,ft是遺忘門的輸出,σ是激活函數,W1是權值,ht–1是相鄰隱含層神經元傳送來的輸出值,b1是偏置。 通過遺忘門遺忘了不需要的數據,再通過記憶們選擇對哪些值進行更新,結合起來的公式為: 其中,Ct是記憶單元的輸出,Ct–1是相鄰隱含層神經元中記憶單元傳送來的輸出,W2是權值,b2是偏置。 隱含層的輸出為:數據由隱含層向輸出層傳播,則輸出層的輸入為: 最終LSTM神經網絡的輸出為: 整個組合模型的流程圖3如下。 圖3 組合模型流程圖Fig.3 Combinatorial model flow chart 本文將這兩個模型組合起來的基本思路為:首先由 ARIMA模型對價格數據的線性成分進行分析預測,該模型只分析、計算前后自變量的關系,使用歷史數據預測當前或者未來時刻的價格數據。通過 ARIMA模型得到線性預測結果,然后用原始數據減去線性預測結果,得到殘差值,該值即為剩下的非線性特征數據;然后由 LSTM神經網絡對只具備非線性特征的殘差值進行分析預測,得到非線性預測結果;最后將兩個模型分別預測的線性結果和非線性結果進行組合,即可得到最終組合模型的預測結果。經過實驗結果分析可知,組合模型預測精度和預測平穩性都有不小的提高,有效解決了單一模型對包含多因素價格序列預測精度不高的缺點。 本文所使用數據為中藥材天地網中亳州市場的人參每kg的市場價格,單位為元,收集的數據自2015年1月至2020年11月,數據如圖4所示。 圖4 人參價格數據圖Fig.4 Ginseng price data graph ARIMA模型的具體實驗步驟如下: (1)平穩性檢驗 由于 ARIMA屬于線性預測模型,而人參價格數據屬于包含線性、非線性等多重因素的序列數據,首先需要對其進行平穩性檢驗,檢驗其是否為只包含線性因素的平穩序列。判斷的依據是進行ADF(Augmented Dickey-Fuller test,單位根檢驗),ADF檢驗是一種較為嚴格的檢驗方法,用以判定序列是否存在單位根。當序列平穩時,不存在單位;而當序列不平穩時,則存在單位根[14]。ADF檢驗先假設存在單位根,如果得到的顯著性檢驗統計量分別小于三個置信度(10%,5%,1%),那么就分別有(90%,95%,99%)的把握拒絕原假設,即序列是平穩的。 先假設序列存在單位根,即先假設該價格其是非平穩序列。P值是指在一定的顯著性水平下,假設統計量正確,臨界值與其相等的概率,所以P越小,拒絕假設的可能性越大,即該序列越有可能是平穩序列。一般認為,P>0.05表示接受該假設,即存在單位根,序列是非平穩的;P<0.05表示拒絕假設,即不存在單位根,代表該序列是平穩的。T檢驗是通過t的分布來比較差異化,若t大于規定水平的臨界值,則接受假設,即序列不平穩;若t小于該臨界值,則拒絕原假設,即序列是平穩的。通過計算可得人參價格序列ADF單位根檢驗結果,具體數值如表1所示。 表1 人參價格序列ADF單位根檢驗結果Tab.1 Test results of ginseng price series ADF unit root 從表1可知,在ADF檢驗下,統計量t=–2.4616,均大于在 1%、5%、10%水平臨界值的統計量,ADF檢驗的概率P=0.4341,大于規定的0.05,因此接受原假設,即該價格序列是不平穩的。 (2)差分 由步驟(1)可知,序列是不平穩的,進行差分處理,值得注意的是,盡管差分運算可消除平穩性,但每一次的差分運算都會使原序列丟失一定的信息,差分次數過多會導致模型不可靠,所以應當使用盡可能少的差分運算。差分后的數據如圖5所示。 圖5 人參一階差分圖Fig.5 Ginseng first order difference map 對差分的金銀花價格序列再次使用 ADF進行平穩性檢驗,結果如表2所示。 表2 人參價格序列ADF單位根檢驗結果Tab.2 Test results of ginseng price series ADF unit root 從表2可知,ADF檢驗下的統計量t=–11.4261,均小于在 1%、5%、10%水平臨界值的統計量,ADF檢驗的概率P=0.0001,小于規定的0.05,所以拒絕原假設,證明該序列是平穩的。確定差分的階數為1。 (1)模型定階 模型定階是通過合適的方法確定 ARIMA模型中p、q兩個參數的值,可通過 AIC(Akaike Information Criterion,赤池信息量)確定[15]。本文通過計算AIC確定ARIMA(p,d,q)種p、q的值。AIC建立在熵的概念基礎上,用來衡量模型復雜度和擬合優良程度。AIC的公式為: AIC數值越小,說明擬合性能越佳。然而模型性能越好,復雜度也會隨著提高,同時似然函數也會增大,并且也可能造成過擬合的現象。為了限制模型的規模,避免過擬合,將值限定在[0,8],通過暴力查找到最合適的值,對應的p、q值為5、5,差分次數為1,即確定模型為ARIMA(6,1,6)。 (2)線性預測 參數全部確定完,模型確立,即可對數據進行訓練、學習、預測,由于 ARIMA模型是使用歷史數據對當前和未來數據進行預測,故2015年1月至2015年6月的價格作為最初的歷史數據無法對其進行預測,以2015年7月為第1個月,2020年11月作為第65個月,預測圖如圖6所示。 圖6 ARIMA線性預測圖Fig.6 ARIMA linear prediction chart LSTM的具體實驗步驟如下: (1)預處理 由于本文是使用LSTM神經網絡預測非線性部分,首先計算人參價格序列的殘差值,ARIMA模型已經預測出人參價格數據的線性趨勢,LSTM 神經網絡只需要對非線性成分進行預測即可。使用人參原始價格數據減去 ARIMA模型的線性預測部分,即使用圖 2.2的數據減去圖 2.4的數據,剩下的殘差值即可認為是人參價格數據的非線性成分。 對該殘差值進行歸一化處理,歸一化可將輸入數據縮放到一個較小的區間,本文將數據歸一化至[–1,1]。由于神經網絡給予數據中偏大的值更多的權重,容易影響預測結果的準確性,而歸一化將所有數據縮放至一定范圍內,可避免這種情況,同時也可以減少計算量、加快收斂。 (2)初始化模型 初始化模型的過程包含數據集的劃分以及輸入特征、隱藏神經元數目的設置。 將處理后包含非線性特征的殘差數據序列劃分為訓練集、測試集,藥材價格數據共有65個,將其中的 40個時間點數據劃分為訓練集,25個時間點數據劃分為測試集,并且對訓練集和測試集數據的選取都是隨機的,但是要保證每次輸入的樣本數據依然具備時間序列特性,即該一個樣本內的數據依然是按時間前后關系排列。隨機選取的目的增加LSTM神經網絡的魯棒性,打亂數據可以在訓練過程中得到不同的梯度,避免每次訓練都從同一個梯度方向尋優,造成過擬合現象。藥材價格預測是使用其本身的自變量對自變量的預測,所以輸入特征為 1。隱含層數目經過多次調試設置為10。 (3)模型訓練 本文的神經網絡實驗基于Keras框架,Keras框架規定LSTM神經網絡的輸入數據格式為:[送入樣本數,循環核時間展開步數,每個時間步輸入特征個數]。送入樣本數確定為 5,即通過前 5個時間點價格數據預測后 1個時間點的價格數據;循環核時間展開步數取 1;每個時間布輸入特征個數因為一個時間點為金銀花一個數據,故取1。 LSTM 神經網絡中訓練學習步驟是整個神經網絡處理過程中最重要的一環,根據價格序列數據的特性和規律,LSTM 神經網絡使用t–1,t–2,…,這些歷史時刻的數據,預測t時刻的數據。確定每一次訓練數據數目為5個,且每個神經元接受1個訓練數據,則輸入層存在5個神經元,實際輸出數據數目為 1。首次輸入后,隱含層的神經元不但要接受輸入層的神經元通過權值計算傳輸的,還要接受同層之中上一個節點傳輸過來的值,并對其進行累加。然后隱含層通過激活函數輸出數據,與真實的輸出數據進行誤差計算,并根據誤差調整權值,以上過程為單次的訓練流程。經過反復的計算,直至誤差低于指定值或者達到一定的次數,則完成訓練。 (4)預測數據 相關數據已經處理完畢,每次訓練以 5個時間點的歷史數據預測未來的1個時間點數據,每個時間點代表一個月的價格數據。多次訓練后擬合出一個對所有訓練數據預測誤差最小的函數,即完成了訓練過程。與ARIMA相同的是,LSTM神經網絡也是使用歷史數據預測未來數據,故2015年7月至2015年12月的數據作為最初的歷史數據無法對其進行預測,重新設置時間標號,將2016年1月作為第1個月,2020年11月作為第59個月。預測圖如圖7所示。 圖7 LSTM殘差預測Fig.7 LSTM residual prediction (5)模型組合 最后一步對模型進行整合,由于兩個模型是分別對線性成分和非線性成分進行預測,模型的整合將兩個模型的對2016年1月至2020年11月的預測結果進行累加。以2016年1月為第1個月,2020年11月為第59個月,最終的預測圖如圖8所示。 圖8 組合模型預測圖Fig.8 Combination model prediction diagram 實驗結果的好壞需要使用相對應的指標進行評析,對于模型的預測精度方面,本文使用MRE(Mean Relative Error,平均相對誤差)對結果進行評價來進行評價;對于模型預測結果的平穩性,本文使用RMSE(Root Mean Square Error,均方根誤差)來進行評價。均方根誤差可以體現誤差的離散程度,即預測的平穩性。平均相對誤差、相對均方根誤差公式為: ARIMA、LSTM神經網絡、組合模型的評價指數如表3所示。 表3 各模型評價指數表Tab.3 Model evaluation index table MRE是誤差與真實值的比例,結果越小越精度越高,RMSE是分析預測結果的離散程度,對異常值高度敏感,即使大多數預測都很準確,一旦有極少數的值與真實值相差較大,那么就會極大的影響RMSE的指標,它的結果越小,預測結果越平穩。從表中可知,LSTM 神經網絡在預測精度和平穩性都要優于 ARIMA模型,而兩者組合的模型在預測精度和平穩性兩個方面都要由于單一的ARIMA模型和LSTM神經網絡。 人參的需求量逐漸擴大,分析其價格走勢并能夠對短期的價格趨勢做出一個準確預測,及時將信息反饋給相關從業者和決策者,這對于種植、銷售和宏觀調控都具有重要意義。應用在人參價格預測上的組合模型的相關研究較少,而藥材的價格數據包含線性、非線性成分,單一的預測模型難免會產生預測精度不高、預測結果不平穩的缺點,本文根據藥材價格數據包含線性和非線性成分的特點選取ARIMA模型和LSTM神經網絡并對其進行組合。 ARIMA模型使用差分法去除原始價格數據中的非線性因素,通過一系列處理從價格序列中提取線性成分,預測出較為準確的線性發展趨勢;LSTM 神經網絡對非線性函數具有較好的擬合能力,而又由于其特殊的結構優勢,對序列數據有更好的預測能力,與 ARIMA模型相結合可以得到更精確、更平穩的預測結果。
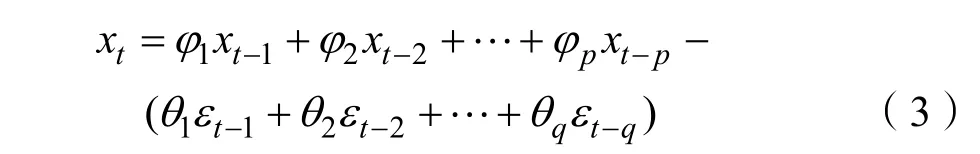
1.2 LSTM神經網絡
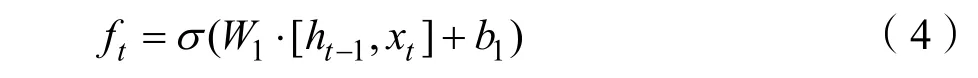
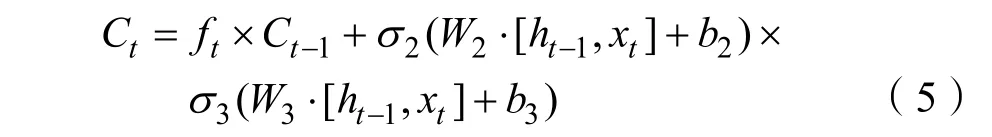
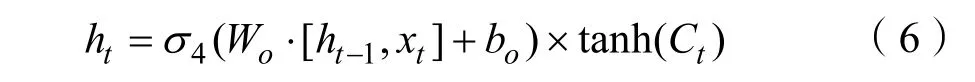


2 實驗流程
2.1 ARIMA模型線性預測

2.2 LSTM神經網絡非線性預測
3 實驗結果分析
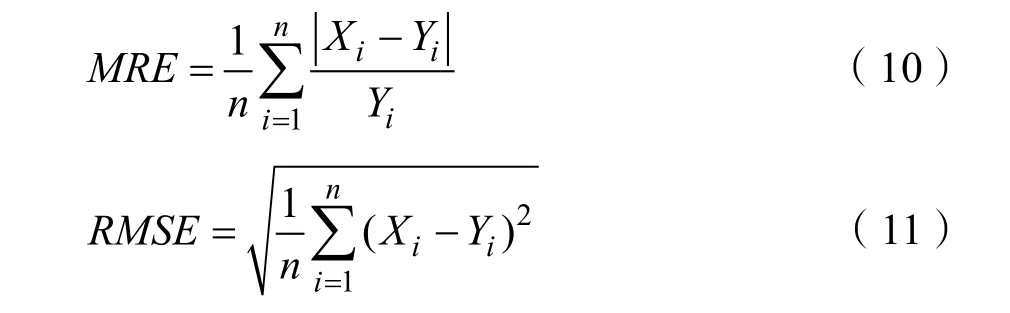
4 結論

