圓柱擾流非定常流動流場動力學模態分解

韋開君，吳 晴，劉立超

(中國電子科技集團公司第三十八研究所 浮空平臺部，合肥 230088)

0 引言

圓柱擾流作為流體力學中的經典問題之一，在化工、建筑、水利、海洋等眾多工程領域都有非常重大的研究意義。國內外學者通過實驗和數值模擬的方法對圓柱擾流問題進行了大量研究，研究結果顯示，盡管流體在經過圓柱后，會產生流動分離、渦脫落以及尾跡相互作用等一系列復雜的流動現象，但其基本特點是存在較為明確的渦脫落頻率[1-2]。相比于常規基于時間歷程的非定常流場分析方法，模態分解方法可以分辨出流場中存在的大尺度有序運動，更加直觀地觀察不同特征頻率下的流動模式及其發展變化規律，特別適合用來描述圓柱擾流的非定常流動特征[3]。

2010年Schmid[4]首次將動力學模態分解(Dynamic Mode Decomposition，DMD)方法引入湍流研究，DMD方法已成功應用于分析各種流體力學問題，例如凹腔流動[5]、動失速尾流[6]、橫向射流[7]、有限平板流動分離[8]、噴管流動分離[9]等。這表明DMD方法是探索復雜非穩態時空流場本質的成熟且有前途的工具。

Tissot等[10]對比了傳統DMD和殘差最小優化DMD方法對圓柱擾流尾跡PIV測試結果分析的影響。張賓等[11]和王智慧等[12]分別應用DMD對旋轉圓柱擾流和橢圓柱擾流的PIV測試結果進行了研究。Stankiewicz等[13]采用DNS直接數值模擬方法對二維和三維圓柱擾流進行了仿真，并應用POD和DMD方法對仿真流場進行分析。Noack等[14]應用DNS方法對旋轉圓柱擾流進行數值仿真，對比了傳統DMD和遞歸DMD對仿真流場分析的影響。在實際工程應用中，PIV測試成本過高，而DNS數值模擬目前尚難以用于真正意義上的工程計算。因此，需要討論采用工程上常用的湍流模型對圓柱擾流進行數值仿真，應用DMD方法進行流場分析的可行性。

本文基于SSTk-ω湍流模型，進行了圓柱擾流的非定常仿真，在時頻分析的基礎上，引入DMD方法對非定常流場進行分析，獲取了各階流場模態的頻率及分布，提取了引起渦脫落的主導模態，并通過模態重構來分析圓柱擾流非定常流動的特征及變化規律。

1 動力學模態分解方法

對于一定時間和空間范圍內的流場數據，在整個可用于分析的時間序列中，流場可表征為一系列離散時間步的“快照”組合(Snapshots) ，如圖1所示。其中，第i個時間步的瞬時流場分布特性可用列向量vi表示：

圖1 流場動力學模態分解原理示意

vi=[u1,u2,…,um-1,um]T∈Rm(1)

式中：uj為j(j∈[1,m])節點上表征流場的物理量(壓力、速度、或密度等)；m為流場的網格節點數量。

式中，n代表離散時間步，則矩陣的維數為m×n。

對流場做線性時不變假設，則可認為vi和vi+1存在線性Koopman映射[15]：

vi+1=Avi(3)

式中，矩陣A∈￡m×m，其特征向量反映了流場內各階模態的空間結構，其特征值則反映了各階模態對應的頻率。因此，基于全局模態分解方法求解流場相干結構的關鍵在于求解矩陣A的特征值和特征向量。一般對于2000階以下的中小矩陣，采用高斯法、QR法等直接方法即可求解。然而，對于一個復雜流場而言，其網格節點m通常遠大于2000，而且矩陣A通常還是稀疏矩陣。對于此類矩陣，通常采用投影類算法，將高維矩陣投影至低維子空間，通過迭代計算其特征值和特征向量。

對于矩陣A和列向量v1，其張成的n維Krylov子空間為：

kn(A,v1)=span{v1,Av1,…,An-1v1}

=span{v1,v2,…,vn} (4)

對于矩陣A和列向量v2，其張成的n維Krylov子空間為：

kn(A,v2)=span{v2,Av2,…,An-1v2}

=span{v2,v3,…,vn+1} (5)

由式(4)和式(5)可知：

當n增加到一定數量時，可認為子空間基底存在線性相關，則有：

Vn+1=h1v1+h2v2+…+hnvn+r(7)

寫成矩陣形式則有：

式中:r為殘差向量;e為n階單位向量，H∈Cn×n為上Hessenberg矩陣，具體可寫為：

vi≈Uμi(10)

FDMD=U*AU(11)

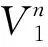
式中:Σ為r×r(r≤n) 的對角陣;U∈￡m×r;W∈￡n×r;星號代表矩陣的復共軛轉置。將式(6)和(12)式帶入式(11)中，則有：

則可直接對FDMD∈￡r×r進行特征值和特征向量求解：

FDMD=YΛY-1(14)

將POD基底空間上的特征向量Y投影回矩陣A，則流場的各階動力學模態為：

Φ=UY(15)

與式(3)類似，在低維POD投影子空間內，有：

μi+1=FDMDμi(16)

將式(14)、式(15)和式(16)帶入式(10)中，則可基于流場的各階動力學模態對瞬時流場進行重構：

式中:向量φ為流場的各階動力學模態;α表示各階動力學模態的貢獻量;λ為矩陣FDMD的各階特征值，則整個時間序列的流場重構可寫為如下形式：

將式(18)帶入式(12)中，可采用GMRES求解得到diag{α}：

上述過程即為流場的動力學模態分解方法。

2 算例與分析

2.1 數值方法

基于二維數值計算模擬了圓柱繞流流場，計算幾何模型如圖2所示。圓柱模型的直徑d=0.04 m，幾何的坐標原點為圓柱圓心，坐標軸X方向為來流方向，進口距離軸心5d，出口距離軸心15d。計算域上下截面關于圓柱對稱，距離軸心5d。

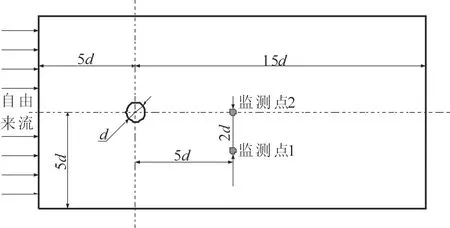
圖2 計算域幾何模型

數值計算采用結構化網格劃分，網格總數為34.7萬。入口邊界條件為沿X方向速度入口，vx=0.15 m/s。出口邊界條件為流出出口，出口壓力為標準大氣壓。上下表面為滑移壁面，滑移速度的大小和方向和進口來流速度相同。圓柱邊界為無滑移壁面。計算的流動介質為水，密度ρ=998.2 kg/m3，動力粘度系數μ=0.001003 Pa·s。本文計算的雷諾數Re=ρvxd/μ=5971，屬于亞臨界區。數值計算采用SSTk-ω湍流模型，邊界層網格劃分保證y+≤0.5。非定常計算時間步長為0.05 s，時間離散采用二階隱式，空間離散采用二階迎風，壓力速度耦合算法采用SIMPLEC算法。計算域設置2個壓力脈動監測點，分別位于距離圓柱后5d的正后方和下方2d處。

2.2 壓力脈動時頻分析

圖3所示為某時刻卡門渦街分布情況。由圖3可知，流體在給定的進口速度流向圓柱后，尾跡發生周期性渦脫落產生了交替的卡門渦街。

圖3 卡門渦街分布

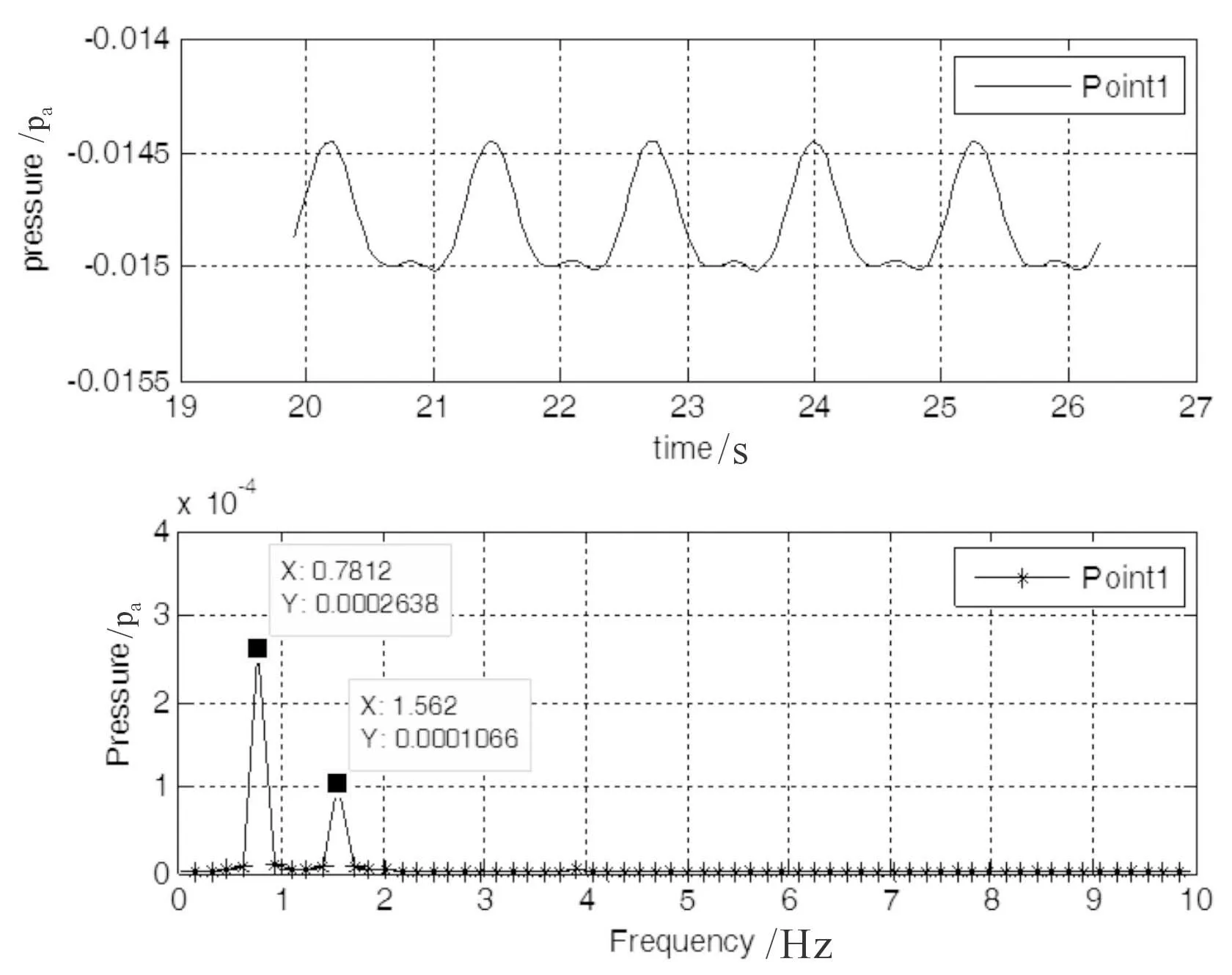
圖4所示為監測點1的壓力脈動時域分布和頻域分布特征。可知圓柱繞流后渦脫落頻率為0.7812 Hz。

圖5所示為監測點2的壓力脈動時域分布和頻域分布特征。監測點2位于圓柱正后方，受到卡門渦街兩側渦脫落影響，其壓力脈動頻率為1.5620 Hz，是渦脫落頻率的2倍頻。

斯特勞哈爾數St是當地慣性力與遷移慣性力的比值，反映非定常流動的周期性[16]。針對圓柱后尾跡周期性渦脫落呈現的“卡門渦街”現象，可用St表示其周期特性。

式(20)中，f為渦脫落頻率，d為圓柱直徑，V0為來流速度。由前文分析可知，仿真計算得到的渦脫落頻率f=0.7812 Hz，帶入式計算得St=0.208。實驗和計算結果表明，在 1500 ≤Re≤ 7200 范圍內，基準圓柱的St數穩定在0.2～ 0.21之間。本文計算的雷諾數Re=5971，斯特勞哈爾數St=0.208，符合文獻[17]給出的St數范圍。

2.3 流場動力學模態分解

采用DMD方法對圓柱繞流流場進行分析，結果如圖6所示。需要指出的是，DMD分解的第一階模態為零頻率模態，表示非定常流場的一個周期內的平均信息，圖6給出的DMD分解結果為去除零頻率模態后的結果。由圖6可知，流場中存在2種非定常流動模態，1階主模態頻率為0.7863 Hz，2階模態頻率為1.5726 Hz。1階模態是流動中最不穩定的模態，全局能量最大，其模態頻率與前文時頻分析中監測點1的壓力脈動頻率0.7812 Hz基本一致，該模態流動特征在圓柱擾流的非定常流動中占主導地位。2階模態頻率約為1階模態頻率的2倍頻，與前文時頻分析中監測點2的壓力脈動頻率1.562 Hz基本一致。

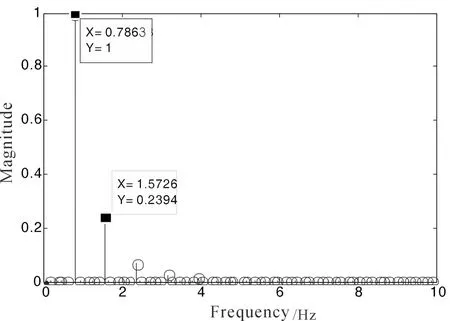
圖6 流場標準動力學模態分解結果

圖7為經DMD分解的1階和2階流場壓力分布特征。由圖7可知，0.7863 Hz的1階模態表現為流體經過圓柱后，在兩側形成周期性對稱排列的旋轉方向相反的雙列渦線，即卡門渦街。1.5726 Hz的2階模態主要表現為在圓柱正后方，對稱排列旋向相反的雙列渦線相互作用形成的類駐波特征。

3 結論

本文采用非定常數值仿真方法對圓柱擾流進行了研究，對流場內典型監測點進行了時頻分析，并引入DMD方法對非定常流場進行分析，獲取了各階流場模態的頻率及分布特征。主要結論如下：

(1)DMD方法可準確提取圓柱后方流場的振蕩頻率，與圓柱后方典型監測點的時頻分析得到的頻率吻合較好；

(2)去除零頻率模態，DMD提取的1階模態表現為圓柱后方兩側形成的雙列渦脫落特征，2階模態表現為兩側渦團在圓柱正后方相互作用形成的類駐波特征。

(3)DMD方法與CFD非定常計算相結合可以作為研究圓柱擾流非定常流動特征的有效工具，并推廣至其他非定常流動問題的分析應用。