淺析總縱彎曲對舷墻強度的影響

盧潤澤 必維船級社（中國）有限公司

在對常規船型的舷墻進行設計或強度校核的過程中，由于舷墻往往布置在船舶艏艉且連續長度較短，因此通常認為舷墻受船體梁總縱彎曲的影響較小，各船級社的規范公式也沒有考慮船體梁應力的影響。但是對于某些特殊船型，例如科考船或輔助用途船，舷墻有時會設計在船舶中段，且有一定的連續長度，此時會有設計人員提出疑問，是否需要在一定程度上考慮船體梁應力對舷墻強度的影響，進而在規范要求厚度的基礎上適當加厚。

針對這種特殊情況，本文以某科考船型為算例，使用有限元方法進行計算，對結果進行屈服及屈曲強度的評估，并與規范現有要求進行對比，為日后的設計及校核工作提供一定的實例依據。

1.有限元模型

1.1 船舶簡介

本文選取國外某科考船型作為算例，該船型0.5L之前為上層建筑，舷墻存在于艉部至上層建筑之間，主要參數見表1。

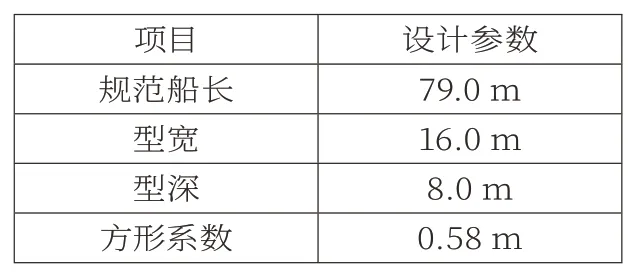
表1 船舶主要參數

1.2 有限元模型建立

1.2.1 建模方法與原則

本次計算使用Fe map 作為有限元建模及后處理軟件，MSC.Nastran作為解算器，對船舶中體艙段進行有限元計算分析。

根據結構特點，采用了板單元、梁單元的適當組合。其中，板單元主要用于模擬甲板板、底板、艙壁板等結構；梁單元主要用于模擬縱骨、艙壁垂直和水平扶強材等構件，并考慮偏心的影響。

1.2.2 模型優化

首先，由于本次分析主要目標為舷墻，因此主船體部分模型僅以中橫剖面為基礎建立，并保證了主要縱橫艙壁對于主船體的有效剛性支撐，并未對過多的小艙室進行建模。

其次，為了能得到比較理想的計算結果，在建立舷墻模型時忽略了一些功能性開孔，如導纜孔或舷墻門等結構。具體模型見圖1。

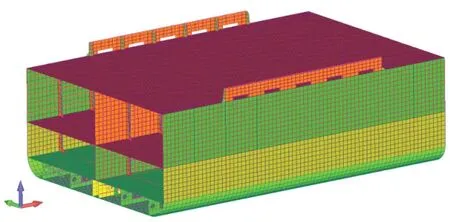
圖1 完整模型

1.2.3 對比模型

另外，為了研究舷墻對于船體梁強度的貢獻，將完整模型中的舷墻結構刪除后再次計算進行對比，工況只按照完整模型中的中拱工況進行分析，邊界條件與加載方式則與完整模型保持一致。

2.載荷選取

2.1 強度計算工況

本次計算僅通過施加總縱彎矩來分析船體梁應力在舷墻中的傳遞分布，不考慮局部載荷對于船體結構的影響，其中靜水彎矩為裝載手冊中的包絡值，波浪彎矩則按照規范[1]公式計算得到，見表2。

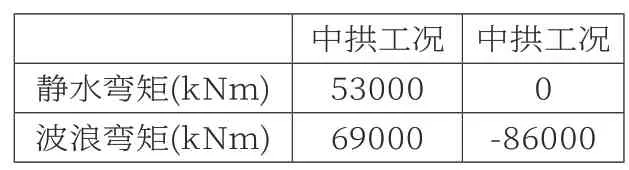
表2 船體梁彎矩

2.2 邊界條件

將目標艙段向前后各延伸兩個強框架，緩沖邊條條件對目標分析區域的影響，將模型一端剛固，另一端各構件所有自由度通過MPC相關到獨立節點，并將船體梁彎矩施加到該獨立節點。

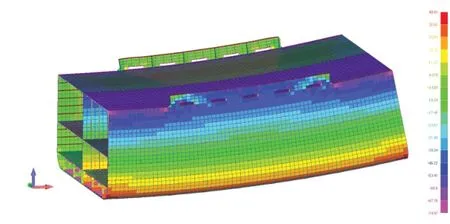
圖3 中垂總縱應力云圖-完整模型

圖4 中拱總縱應力云圖-無舷墻模型

3.結構強度分析

分析得到的應力分布如圖2-4所示，其中右舷應力云圖為x向中面應力，等同于船體梁應力。

圖2 中拱總縱應力云圖-完整模型

根據BV規范，該船舷墻要求的最小厚度為6mm，設計厚度為8mm。按照規范對舷墻板格分別進行屈服屈曲評估，并將評估結果分別于上述值進行對比。計算過程中局部海水壓力按照規范公式計算，船體梁應力則從有限元分析結果中讀取。

3.1 屈服強度評估

考慮屈服影響的板厚計算公式為：

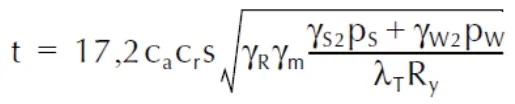
式中：

ps——海水靜載，0kN/m2；

pw——海水動載，7.1kN/m2；

τ1——船體梁剪應力，0N/mm2；

σx1——船體梁正應力，68.3N/mm2；

其余參數見規范定義。

計算得到的要求板厚為3.19mm，結果遠小于規范要求最小板厚，評估結果安全。

3.2 屈曲強度評估

屈曲評估采用僅雙邊受壓受彎的屈曲模型，僅讀取中垂工況下的船體梁應力進行屈曲分析。

考慮屈曲影響的板厚計算公式為：

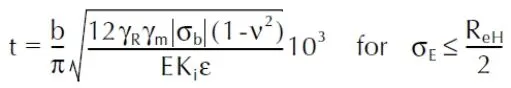
式中：

σb——船體梁壓應力，54.39N/mm2；

σE——歐拉屈曲應力，63.72N/mm2；

其他參數見規范定義。

計算得到的要求板厚為7.85mm，已經超過規范要求最小板厚，但是仍小于設計板厚，評估結果安全。

4.結論

首先，通過觀察應力分布可以看出，舷墻的中段區域應力大小已經與舷頂列板處幾乎一致。盡管排水舷口設置較為密集，但是由于舷墻的橫向支撐肘板被主船體強框架有效支撐，受主船體整體變形的影響比較顯著，迫使舷墻參與總縱彎曲。

其次，經過對比計算結果可以看出，船體梁應力對于舷墻的屈服安全性影響不大，但是在屈曲安全性方面，板厚要求值已經超過規范要求的最小厚度且十分臨近設計值。因此，當船型尺寸繼續增大時，應當增加相應的屈曲計算來考慮總縱彎曲對于舷墻的影響，或者在設計過程中增加舷墻門或者欄桿之類的設置來打斷舷墻的連續性，降低舷墻參與總縱彎曲的百分比。

值得注意的是，對比完整模型與無舷墻模型的計算結果，發現舷頂列板處的船體梁應力變化不大，可以看出盡管舷墻參與了總縱彎曲，但對船體梁強度的貢獻不大。因此，在日后的設計過程中，針對這種特殊船型，可以從常規的無舷墻模型中先讀取舷頂列板處的船體梁應力，用來對舷墻進行試算分析，通過試算結果來大致評判是否需要對舷墻作進一步的有限元分析。